Hungarian algorithm in the task of tracking a multitude of moving objects

I want to talk about the well-known, but poorly lit in the literature approach to tracking a multitude of moving objects. The complexity of this task largely lies in the fact that the algorithms for detecting and selecting objects often fail, and the objects themselves can be obscured by other objects and background elements.

In the general case, the solution of the tracking problem contains three main steps:
- selection of segments;
- mapping between the selected segments and the monitored objects;
- clarification or prediction of the position of objects of interest.

In this case, a segment is called a connected region of the image, which is allocated on the basis of motion. In the framework of this note we will be interested in the 2nd and 3rd of the listed stages.

General formulation of the problem

We assume that in the current frame, one or more segments are selected on the basis of motion. To do this, you can use background subtraction, optical flow, methods based on a mixture of Gaussian distributions, etc. As a result, instead of the original halftone image, we obtain a binary image, as shown in the figure below.
')


In view of the presence of noise and various atmospheric distortions, the results of the selection contain errors that can be easily eliminated using the methods of mathematical morphology. First, a morphological discovery should be applied, which will allow to remove small-sized segments and point noise. Then you can apply morphological closure to restore the shape of objects. As a result, we obtain a cleaned image (see figure), which is further subjected to markup and parameterization. The list of found segments and their parameters are the initial data for the tracking algorithm.



So, as a result of the algorithm for selecting objects, a list of segments detected on a given frame can be obtained; however, to solve the problem of tracking objects, you must match each of these segments with an object known in the previous frame, or decide to discover a new object. Sometimes erroneously detected segments are fairly stable in time and exist at close points in space over several frames. On the other hand, sometimes correctly detected segments disappear for a short time. Therefore, there should be a mechanism that, firstly, makes a decision on the detection of a new object, secondly, filters time-unstable false segments, thirdly, establishes a correspondence between previously known objects and new segments, fourthly, predicts the coordinates of objects in the case of a short-term disappearance, fifthly, it makes a decision about the loss of the object.

To make the tracking algorithm resistant to the temporary closure of an object with background areas for each object, a personal trajectory filter is introduced, the main task of which is to predict the coordinates of the object in the next frame based on the analysis of the object's trajectory. Usually, the Kalman filter is used as such a filter.

When the object is temporarily closed by background areas or other objects, the trajectory parameters are not refined, and the trajectory filter works in the coordinate prediction mode.

If there are multiple tracking objects in a sequence of images, there is a probability of objects being confused in situations of intersection of their movement trajectories. After the intersection of the trajectories, the objects must receive the same identifiers that they had before the intersection. An example of proper assignment of identifiers is shown in the figure.

Object tracking based on the Hungarian algorithm

As a first step of the tracking algorithm, it is necessary to establish a correspondence between the segments found in the current frame and the objects tracked. For this purpose, a quantitative measure of similarity is calculated between each i -th object and each j -th segment. As such a measure, you can use the Euclidean distance between the predicted coordinates of the object and the center of the segment 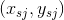i.e.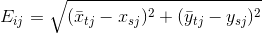



It should be noted that new objects may appear on the image, and objects traced for some time may leave the frame limits or temporarily obscure obstacles. We will consider three types of situations:

a) a match is found between the object and the segment;

b) no match was found for this object among the segments;

c) for this segment no match was found among the objects.

The Euclidean distance can be considered as the cost of deciding (a) on the correspondence between the i -th object and the j -th segment. We introduce the quantity E _t , which sets the cost of the solution (b), and the quantity E _s , which sets the cost of the solution (c).

As a result, we arrive at the solution of the following problem: it is necessary to establish the correspondence between the segments and the objects or decide that such a comparison is impossible so that the total cost of all decisions is minimal. This task is known as the assignment problem; the Hungarian algorithm is used to solve it.

To apply the Hungarian algorithm, it is necessary to compose a square matrix of value of size N _M = N _t + N _s , where N _t is the number of objects tracked, and N _s is the number of segments found. The cost matrix has the following form:



where D _max is a large enough number, such that D _max >> E _ij . The monitored objects are counted by the rows of the matrix, the found segments are by the columns.

As a result of the execution of the Hungarian algorithm, we obtain a list of pairs (t, s) _k , k, t, s = 1..N _M.

If t <= N _t and s <= N _s , then a correspondence is established between the t -th object and the s -th segment [situation (a)].

If t <= N _t and s> N _s , then for the t-th object there is no corresponding segment found [situation (b)].

If t> N _t and s <= N _s , then no suitable object was found for the s-th segment [situation (c)].

Each of these situations leads to the need to perform different actions. In the first case, you should update the list of object parameters based on the parameters of the segment corresponding to it. In the second case, the update is not possible, however, the absence of the corresponding segment can be explained by the temporary blocking of the object. Therefore, in this case, it is necessary to proceed to predicting the parameters of the object on the basis of previous observations. To clarify and predict the coordinates of objects, the Kalman filter is used. Finally, in the third case, the segment corresponds to the newly appeared object.

During the observation, objects may leave the frame limits. In this case, you should stop tracking them. The criterion for determining such situations is the impossibility for a sufficiently long time to establish a correspondence between this object and any of the segments selected in the current frame.

Of course, the scheme described above is quite simple. In more complex scenarios, you would have to handle object obstructions by merging and splitting tracks. However, this is a completely different story ...