Night hall. Thousands of mysterious faces in the dark, illuminated by the bluish glow of monitors. The deafening crackle of a million keys. Similar to shots of a machine gun, hitting the “Enter” keys. The ominous chirping of hundreds of thousands of mice ... So, for certain, the imagination of every developer of a highly loaded system played. And if it is not stopped in time, then a whole thriller or horror movie can come out. But in this article we will be much closer to the ground. We briefly consider the well-known approaches to solving the problem of search hints, how we learned to make them full-text, and also tell about a couple of tricks that we went to give them speed, but it does not teach greed for resources. At the end of the article you will find a bonus - a small working example.

What should be "under the hood"?

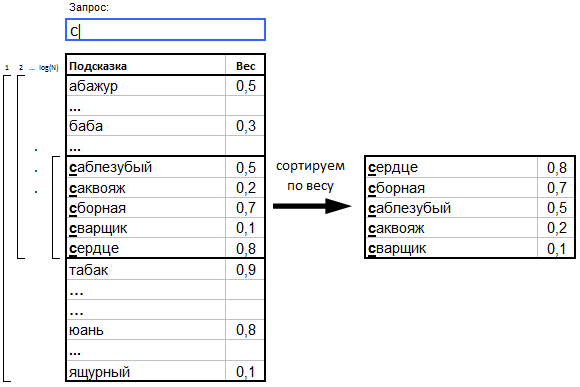
1. Search by prompts should be full-text , that is, should be able to search through the texts of prompts all the words from the user query in any sequence. For example, if the user entered the query “view” , and in the database we have the following prompts:
   
   
   
   then the user should see all three, despite the fact that the word "look" is in different places of these prompts.
2. A user request may be incomplete while typing it on the keyboard. Therefore, you need to search not by words, but by their prefixes. For the previous example, we should see all three hints not only for the whole word “look”, but also for any of its prefix parts. For example, " review ".
3. Mail.Ru search is a general purpose search engine, which means that the variety of possible queries is large, and the system should be able to search among tens of millions of clues.
4. The speed of the reaction is extremely important, so we want to give an answer in milliseconds.
5. Finally, the service should be a reliable system operating in 24/7/365 mode. From all over Russia and the CIS countries, our prompts every second process thousands of requests. For fault tolerance, and, therefore, for the sake of ease of implementation and debugging, it is highly desirable for us to have some kind of idea at the heart of the service that would be extremely simple and elegant.

Known approaches

1. Prefix autocompletion

a. Tips with weights (weight == popularity) are sorted in lexicographical order by hint texts.
b. When a user enters a query (prefix), a binary search is a subset of prompts, the beginning of which satisfies this prefix.
c. The found subset is sorted by descending weight, and the TOP of the “heaviest” prompts is given to the user as a result.
')


The obvious optimization of this approach is Patricia Tree with weights in the nodes of the tree. When selecting the most "heavy" queries, as a rule, a queue with priorities is used , or a segment tree , which gives a logarithmic search time. If you wish, you can spend the server memory using the LCA algorithm via RMQ , and then we get very fast prefix prompts . There are three advantages to this approach: speed, compactness and ease of implementation. However, the obvious and most unpleasant drawback is the impossibility to look for word swaps in the text of hints. In other words, such hints will only be prefix, not full-text.

2. Full-text autocompletion

a. The texts of the prompts and the user's request are considered as a sequence of words.
b. When a user enters a query, a subset of prompts is searched in the database, which contain all the user's words (or rather, prefixes), regardless of their position in the prompt.
c. The found subset is sorted by descending words matching the hint to the words of the query, then descending by weight, and the user gets the TOP “heaviest”.



Actually, this is the full-text approach, which will be discussed later. An extensive number of publications by domestic and foreign authors are available on this topic on the Internet. For example:

• The implementation of a fuzzy search - the author has implemented search hints for the names of bars, restaurants and other institutions, combined with the correction of typos. Since there were only ~ 2.5 thousand prompts, it turned out to be enough to search through all the prompts using the Wagner-Fisher algorithm, which was modified to search for word prefixes. The method is qualitative, but does not suit us due to low speed.
• TASTIER approach is a live-search for articles that finds not only an exact match, but also related publications. It stores the user's context in RAM in order to adapt it as a user request is entered, which is quite expensive in memory and detrimental to speed.
• Sphinx Simple autocomplete and correction suggestions - autocompletion based on the well-known open search engine Sphinx. The main idea of ​​autocompletion is to use wildcard in the MySQL query language: “ the wor * ”. The correction of typos is based on the n-gram approach . Of course, such a search is not exactly what we need: after all, the user does not necessarily type the last word; and as practice shows, the user can enter the words of the query as you like, in any sequence. In addition, the n-gram approach will require a lot of resources to apply it in real-time prompts.

The above and other approaches not considered here did not satisfy us in combination: economy + speed + simplicity. Therefore, we have developed our own algorithm that meets our needs.

Formal statement of the problem

Before describing the algorithm, we formulate our problem more formally. So, given:

• The set of hint texts is S = {s ₁ , s ₂ , ..., s _N }, each of which consists of the words W (s _i ) = {w _i1 , w _i2 , ..., w _iK }. We get the text of hints from the logs of the queries that users specify to our search engine.
• The set of the popularity scales of the prompts F = {f ₁ , f ₂ , ..., f _N }. Here, by popularity, we mean the frequency of use of a particular query, that is, how often users search for something in our search engine for a given query.
• Incomplete user request consisting of an ordered sequence of prefixes Q = {p ₁ , p ₂ , ..., p _M }. As we said above, we view the user's request as a sequence of prefixes, since the request may be incomplete.

Required:

• Find the set R of all prompts s _i from S, such that each prefix p _j from Q corresponds to one unique word w _k from W (s _i ).
• Sort the found set of tips R by two criteria:
  
  • by descending order correspondence of words w _k from W (s _i ) to the order of prefixes p _i from user request Q;
  • descending weight popularity f _l from F tips s _i from R.
  
  

Index

Since we need full-text search through prompts, then our index is based on a classic approach to the implementation of a general-purpose full-text search, on which any modern web search engine is based. In general, full-text search is conducted among so-called documents, that is, texts within which we want to search for words from a user's request. The essence of the algorithm is reduced to two simple data structures, direct and inverse indices:

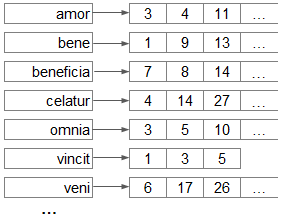
• direct index - a list of documents in which you can find this document by its id. In other words, a direct index is an array of strings (a vector of documents), where the id of the document is its index.
  
  
  
  
• reverse index - a list of words that we "blew out" of all documents. Each word is assigned a list of sorted id documents (posting list) in which this word is found.
  
  

For these two data structures, it is easy enough to find all the documents that satisfy the user query. For this you need:

1. In the reverse index: according to the words from the query, find the id lists of those documents where these words were encountered. Get the intersection of these lists - the resulting list of id documents, where all the words from the query are found.
2. In the direct index: using the obtained id, find the source documents and “give” them to the user.

This is quite enough for this article, so for details about the search, we refer you to Stanford University’s book An Introduction to Information Retrieval .

The classic algorithm is simple and good, but in its pure form it is not applicable to prompts, because the words in the query are generally “unfinished”. Or, as we said above, a query does not consist of words, but rather of prefixes. To solve this problem, we finalized the reverse index, and this is what we did:



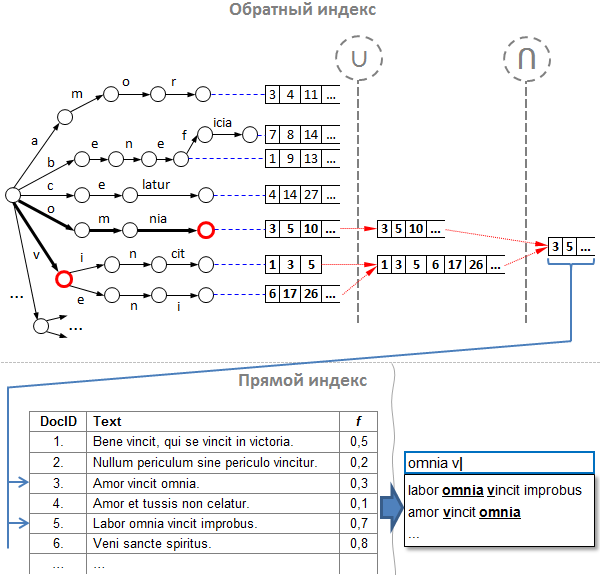
Note : in the picture hereinafter for brevity, some nodes of the tree are “merged” into one transition of several characters.

Let's sort the index by example:

1. Suppose that we have the above index, and the user has already entered part of the request. The next letter entered on the keyboard, and now we received an incomplete query “ omnia v ”.
2. We split the query into prefix words: we get “ omnia ” and “ v ”.
3. By analogy with the search engine, first, using predefined prefix words, we find lists of id prompts in the reverse index. Note that our reverse index consists of two parts:
   a. a prefix tree (it is also “trie”, it is also “bor”), containing words that we “gutted” from the hint texts;
   b. tips id lists - indexes of the text of hints in the direct index, which will be discussed below. Lists are sorted in ascending id values ​​and are located in those vertices where words end.
   I must say that trie is good for us for two reasons:
   
   • it can be used to find any word prefix in O (log (n)) time , where n is the prefix length;
   • for a given prefix, it is easy to determine all variants of its continuations.
   
   So, for each prefix we go deep down the tree and find ourselves in intermediate nodes. Now you need to get the correct lists of tips ids.
4. We unite lists of all child nodes. For what? By analogy with the usual search engine, we should cross the lists of id for each prefix, however there are two “BUT”:
   a. first, not every node contains a list of id prompts, but only those nodes in which the whole word is being pumped;
   b. and secondly, each tree node has some continuation, with the exception of leaf nodes. This means that the continuations of one prefix can be a whole set, and these continuations must be taken into account.
   Therefore, before you find a suppression, you need to "sum up" the lists of id prompts for each individual prefix. Thus, for each prefix we go around the tree recursively into depth, starting from the node where we stopped in the tree using the given prefix, and we construct the union of all the lists of its children by the merge algorithm. In the figure, the nodes where we stopped by the prefix are marked with a red circle, and the merge operation is marked with a “ U ”.
5. Now we intersect the synthetic lists-associations of each of the prefixes. It must be said that the various intersection algorithms of sorted lists are simply a sea, and each one is more suitable for different types of sequences. One of the most effective is the algorithm of Ricardo Baeza-Yates and Alejandro Salinger . In the combat prompts, we use our own algorithm, which is most suitable for solving a specific problem, but the algorithm of Baeza-Yates-Salinger was inspiring for us at one time.
6. Now, by the id found, we are looking for hint texts. The direct index in our case is no different from the direct index of any search engine, that is, it is a simple array (vector) of strings. In addition to the text of hints here can be any additional information. In particular, here we store the weight of popularity.

So, by the end of the sixth stage, we already have all the prompts that contain all the prefixes from the user request. Obviously, in fact, the number of hints we get to this stage can be very many - thousands or even hundreds of thousands, and we only need the best to “prompt” the user. This problem is solved by another algorithm - the ranking algorithm.

Next, we will look at one small trick that will allow us to “half” otranzhdiruya tips, doing absolutely nothing. And we'll talk about it below, in the course of the consideration of two problems.

Speeding up

“Premature optimization is the root of all evil” - repeats popular programmer wisdom formulated by Donald Knut. But if we implement the above algorithm in its pure form, then we grab two performance problems. Therefore, for us, the absence of a struggle for speed will be that evil.

The first problem is the slow merging of lists . Consider this problem in more detail:

1. Suppose, in our tree (traa), there are already 1000 words beginning with the letter “ a ” (in a real situation there are even more such words).
   
   
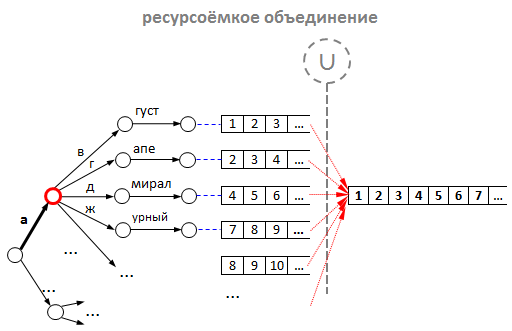
2. It is obvious that for 1000 words the minimum average number of id prompts will also be about 1000. That is, there will be at least 1000 prompts on average, in which there are words beginning with the letter “a”.
3. Now imagine that the user decided to search for something with this letter " a ". According to our algorithm, for the prefix “a”, the operation of combining lists for all child nodes that lie below node “a” begins. Obviously, this operation will require decent resources: firstly, to allocate memory for a new list, and secondly, to copy id into this new list.

Combining can be optimized using two techniques:

• reserve memory for the final list, so as not to allocate it with each new request;
• to unite in a "lazy" way, that is, as necessary.

However, our experiments have shown that any tricks with the union can not be compared with optimization due to caching. Yes, yes, we simply began to add id prompts to each node of the tree, and not just to leafy vertices. Total: there is no need to combine - ready lists for each possible prefix are right in the nodes of the tree. And our reverse index has acquired the following form:



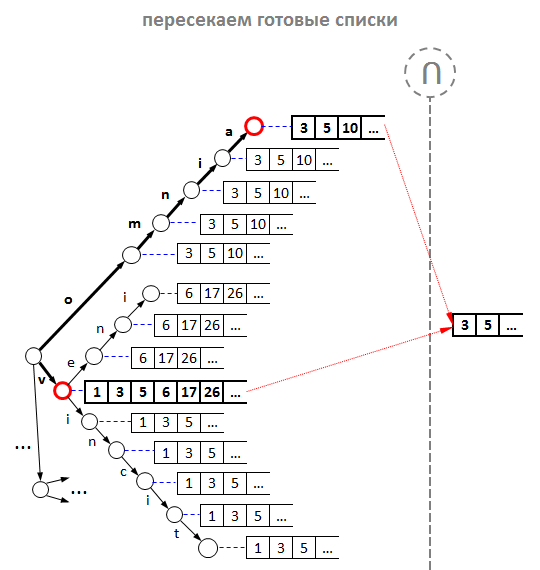
But stand still! In each node of the tree to put the id of the tooltip ?! It looks extremely wasteful, is not it? But is it wasteful? We reason:

• For each new hint, we will have to add its id as many times as there are characters in its text. This is in the worst case, since there is no need to add id spaces, and for duplicate words (“Winnie the Pooh and everything is all ”), it is not necessary to add an id again.
• For example, with an average prompt length of 25 characters, 1 million search hints contain 25 million characters. And if the id of the hint is a 4-byte integer (standard int), then in the worst case, all the lists of the id of the hints in the reverse index will be in memory: 4 bytes * 25,000,000 = 100 MB . And such a volume, obviously, is not so wasteful, even for an ordinary person. In proportion, for 50 million prompts, the index will take 5 GB, which is quite appropriate for a full-scale search engine service.

So, we solved the problem of combining lists by caching all lists for each possible prefix.

The second problem is the slow intersection of lists and the ranking (sorting) of weight tips . According to our algorithm, two important steps follow after merging, and each has performance problems:

1. Intersection of merged lists. In a large database, real lists are too long, especially for short prefixes. Therefore, the intersection of lists for short queries, like “ a b ”, will be too long.
2. Ranking tips, above all, by decreasing weight. The final list after the intersection can also be quite large, so sorting thousands of id, as for the query " a b ", also turns out to be expensive.

Remembering that for the result we need only 7-10 "very good" tips, we found a very simple solution, which consists of two points:

1. The correct order is id prompts. We make lists of id in such a way that the hint with the greatest weight has the smallest id. In other words, hints need to be added to the index in descending order of their weight. Thus, the resulting list after the intersection will be sorted at the same time in descending order of weight and id value. We call this approach “ pre-ranking ”.
2. We do not need a complete intersection. It was established experimentally: when crossing, you can take not everything, but it is enough to take the first K prompts (where K> N and in proportion to the target number of prompts N), and among them there are already those from which you can choose something suitable as by weight, and in word order. For example, if we need TOP N = 10 of the most good prompts, then we only need to choose from the resulting intersection about the first K = 100. For this, at the intersection, we can count how many id in the resulting list, and as soon as we have typed the first 100, we stop intersection
   
   
   
   

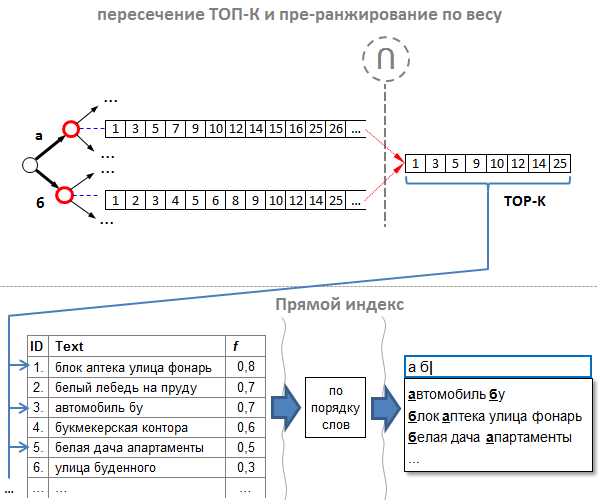
Thus, we optimized both the weight ranking and the intersection to the “lazy” K first clues.

Implementation

As promised in the beginning, we post a working C ++ example that implements the algorithm described in the article. As a source base, you can use any text file, where each line is a hint. You can fill it, for example, with proverbs and winged expressions in Latin ( primary source ) in order to be able to quickly receive their translation into Russian and vice versa.



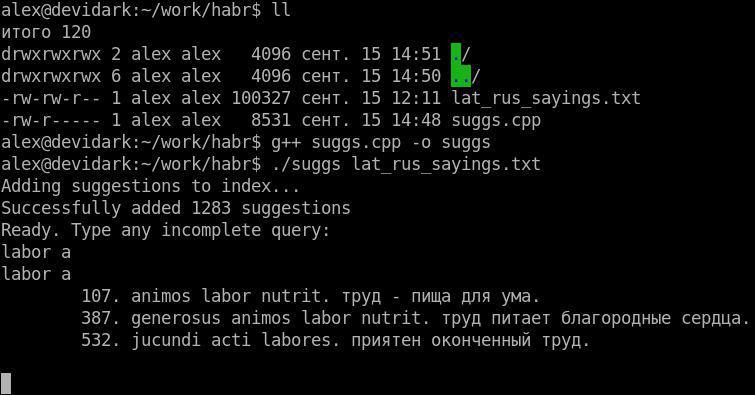
We will not dwell on the features of the implementation, giving it to the reader: the good example is quite simple.

Instead of a conclusion: what is left "overboard"

Of course, the algorithm presented here is described in the most general form, and many questions were left out of the scope of the article. What else it would be useful to think of the hint developer:

• algorithm for ranking hints taking into account the positions of words;
• Invert the keyboard language layout: “ghbdtn” -> “hello” ;
• correction of typos in a user request; here we will send you to a good article from Microsoft developers: S. Chaudhuri, R. Kaushik, Extending Autocompletion To Tolerate Errors ;
• constructing the user's request ending for the case when we have nothing to tell from the base of the prepared hints: “what sang in the mid-80s alla poo” -> “what sang in the mid-80s alla pugacheva” ;
• taking into account the user's geography: “cinema” -> for a user from Saratov you should not suggest Moscow and St. Petersburg cinemas, which are often sought because of the large audience of users;
• scaling the algorithm for 2, 3 or more servers when we want to add 100-200-500 million hints and focus on memory and processor resources;
• and so on and so forth, that only can be oriented to our favorite user and our needs.

That's all. Thanks for attention.

Alex Medvezhek,
Search Engine Tips .