Another algorithm for determining the intersection of two segments

Recently there was a publication "A simple algorithm for determining the intersection of two segments . " I decided to try to solve the problem of intersection of two segments a little differently, more geometrically.

Finding the point of intersection of two segments.

We have 2 segments {P0, P1} and {P2, P3}, where P0, P1, P2, P3 are points on the plane. We denote the xy coordinates of the point P as Px and Py
We have the coordinates of 4 points in the array P (0..3) of the point (x float, y float) structure:


')
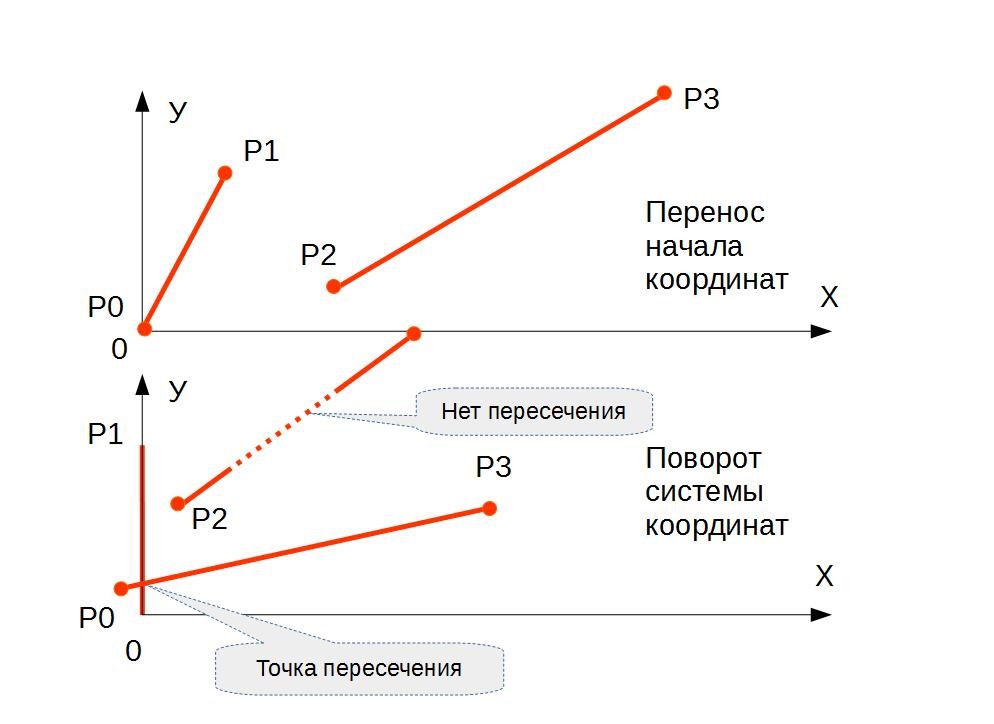
Step 1 - Transferring the origin.

Remember the coordinates of points P in the additional array P_copy. Transfer the origin of the coordinate system to the point P0 and recalculate the coordinates of the points:

P_copy = P P(0).x = 0 ; P(0).y = 0 for ii = 1 to 3 P(ii).x = P(ii).x - P_copy(1).x ; P(ii).y = P(ii).y - P_copy(1).y next 

Step 2 - Rotate the origin
Rotate the coordinate system so that the segment {P0, P1} takes the vertical position (lay on the Y axis). Calculate the length of the segment {P0, P1} as:
L1 = SQRT ( (P(1).x)^2 + (P(1).y)^2 )

Sine and cosine of the angle of alfa rotation of the axes:

   L1 > 0 sin_alf = sin(alfa) = P(1).x / L1 cos_alf = cos(alfa) = P(1).y / L1  L1 = 0 //    sin_alf = 0 cos_alf = 1 

Again recalculate the coordinates of the points P1, P2, P3:

  P(0).x = 0 ; P(0).y = 0 //  P0  ,     P(1).x = 0 ; P(1).y = L1 P(2).x = P(2).x * cos_alf - P(2).y * sin_alf P(2).y = P(2).y * cos_alf + P(2).x * sin_alf P(3).x = P(3).x * cos_alf - P(3).y * sin_alf P(3).y = P(3).y * cos_alf + P(3).x * sin_alf 

Step 3 - Search for the intersection point of the segments.

We write the equation of the segment {P2, P3} and find its intersection point CR with the Y axis:

P23X = P(2).x + ( P(3).x - P(2).x ) * beta

P23Y = P(2).y + ( P(3).y - P(2).y ) * beta

where 0 <= beta <= 1

At the CR intersection of the segment {P2, P3} with the Y axis:
P(2).x + ( P(3).x - P(2).x ) * beta =0

Further, there are 2 options, depending on the value of P (3) .x - P (2) .x:

1 option:

   ( P(2).x - P(3).x ) <> 0 //  {P2,P3}   beta = P(2).x / ( P(2).x - P(3).x )  beta >= 0  beta <= 1 //  {P2,P3}   Y CR.x = 0 CR.y = P(2).y + ( P(3).y - P(2).y ) * beta //  : 0 <= CR.y <= L1 

Option 2:

If P (2) .x = P (3) .x, then this means that the segment {P2, P3} is vertical and parallel to the segment {P0, P1}. Intersection of segments is possible only if the second segment {P2, P3} also lies on the Y axis, and one of its ends lies in the first segment {P0, P1} (or touches) or the segment {P2, P3} covers {P0, P1}. We assume that for the result we need one point. This will be one of the points P0..P3.

Conditions:

  P(2).x = P(3).x = 0 //   {P2,P3}  b    Y.  //  : P(2).y >= 0  P(2).y <= L1 // P2   {P0,P1} -> CR = P_copy(2) //    P2  P(3).y >= 0  P(3).y <= L1 // P3   {P0,P1} -> CR = P_copy(3) //    P3  P(2).y < 0  P(3).y > L1 //  {P0,P1}   {P2,P3}  P(3).y < 0  P(2).y > L1 -> CR = P_copy(0) // //    P0 ( P1) ) 

Step 4

If the intersection point of CR is found by option 1 of step 3, then its coordinates are recalculated for the original coordinate system. We use the variables saved in step 1 and 2. Rotate -alfa angle:

  CR.x = CR.x * cos(-alfa) + CR.y * sin(-alfa) = CR.x * cos_alf + CR.y * sin_alf CR.y = CR.y * cos(-alfa) - CR.x * sin(-alfa) = CR.y * cos_alf - CR.x * sin_alf 

Transfer back:

  CR.x = CR.x + P_copy(0).x CR.y = CR.y + P_copy(0).y 

If the intersection point CR is found by condition 2 of step 3, the coordinate recalculation is not needed. Sample code for golang under the cut. Golang ohm, I just indulge, so I ask the code to be indulgent. The code can be run on golang.org :