Spectral method on the example of simple problems of mathematical physics
This article describes a pseudo-spectral method for the numerical solution of the equations of mathematical physics, used in computational fluid dynamics, geophysics, climatology, and in many other fields.

First, consider the simple one-dimensional problem of heat distribution in the rod. The equation describing the distribution of heat at some initial temperature distribution over the rod:
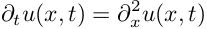
')
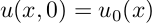
Such an equation is solved analytically by the method of separation of variables, for example, here , but we are interested in how this can be done numerically. First of all, you need to decide how to calculate the second spatial derivative with respect to x. The easiest way to do this is by some difference method, for example:

But we will do otherwise. The temperature distribution is a function of the coordinate and time, and at each moment of time this function can be represented as the sum of the Fourier series, which is numerically truncated on the nth term:

Where u ^ "with a cap" is the decomposition coefficient of a Fourier series. Substitute the expression for the series in the equation of heat transfer:
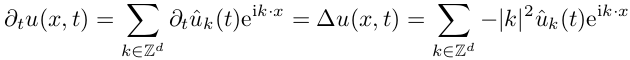
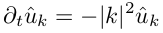
We obtain the equation for the Fourier coefficients, in which there is no derivative with respect to the coordinate! Now this is an ordinary differential equation, and not in partial derivatives, which can be solved by a simple difference method. It is already easier, now it remains to find the decomposition coefficients, and the fast Fourier transform (further FFT) will help us a lot with this.
The logic is as follows:
1) at the initial moment of time, a coordinate function is given that describes the temperature distribution over the rod;
2) we divide the rod into a grid of n points;
3) we find the complex Fourier coefficients using the FFT algorithm, we denote the operation as F (u);
4) multiply the obtained coefficients by - | k | 2 , we obtain the Fourier transform of the second derivative. Similarly, one can obtain the Fourier transform of a derivative of higher orders of p, it is sufficient to multiply by (ik) p ;
5) we do the inverse Fourier transform F -1 (u), using the IFFT algorithm, we obtain the values of the second derivative at points on the grid;
6) make a step in time, already an ordinary difference, explicit or implicit, scheme;
7) repeat.
We now consider how it works in the program for Matlab / Octave. As the initial temperature distribution, we take the smooth function u0 = 2 + sin (x) + sin (2x), split the rod of length 2π into 50 points, with a time step h = 0.1, the boundary conditions are periodic (ring).
It is worth noting a feature of the FFT algorithm in Matlab, which is related to the fact that the resulting expansion coefficients at the output d = fft (u) do not go in order, but are displaced, the first half in place of the second and vice versa. At first, there are coefficients with numbers from 0 to n / 2-1, then with numbers from -n / 2 to -1. There were problems with it ...
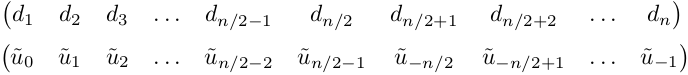
The resulting solution can be seen on the graph as a “waterfall” of temperature distribution lines in x for each time point t. It is seen that the solution undergoesstrong oscillations, numerical instability, this is due to the non-fulfillment of the Courant criterion . One can get rid of instability by reducing the time step, or by applying a more advanced implicit scheme, for example, Crank-Nicholson .

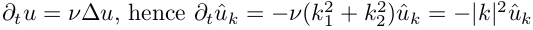
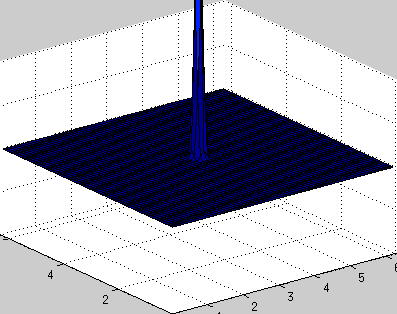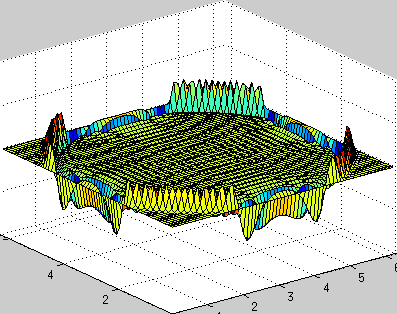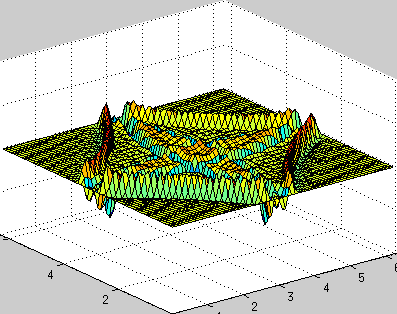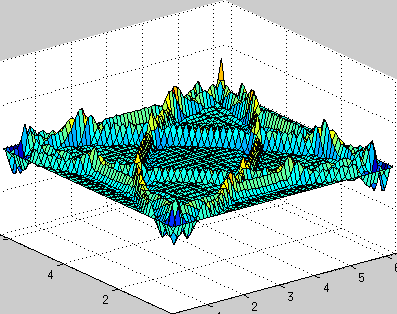
The initial conditions are: u0 = 1 + sin (2X) + cos (2Y), where u is now a 2d array u (i, j). We use an implicit time integration scheme (that is, we express m + 1 step in mth):
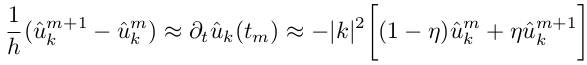
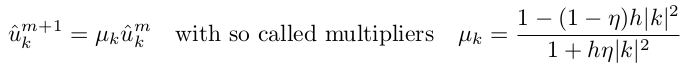
It can be proved that such an implicit scheme never diverges at η> 0.5; we will use η = 1. Thus, each new value of u m + 1 is obtained by multiplying u m by the coefficient μ k , depending on the time step and the wave numbers k, i.e. μ k is a constant that does not need to be recalculated at each step!


There is a second time derivative in the wave equation, so the task is reduced to a system of two ordinary diffuros, one variable is u, the second is u t , the time scheme in the code used the simplest explicit, so the accuracy is small, the time step is very small, but the code looks relatively simple. However, this is enough to demonstrate the efficiency of the method.
Periodic boundary conditions:
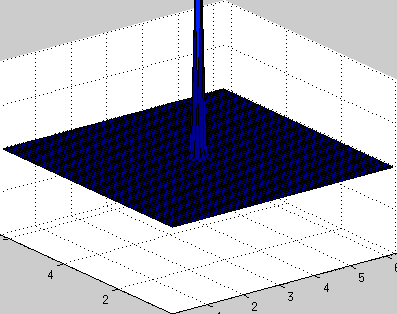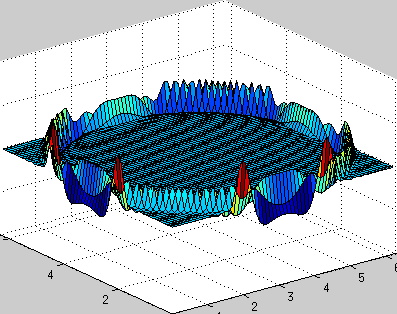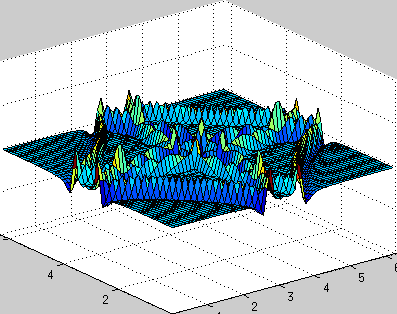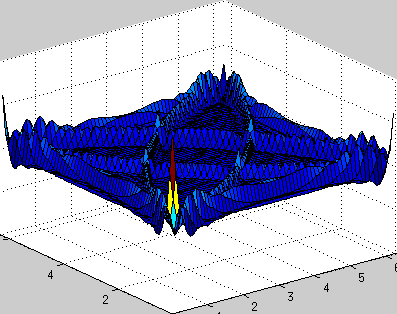
Fixed boundary conditions (0 at the edges, reflection of waves from the boundaries):
The article demonstrates several examples of the application of the spectral method for simple problems of mathematical physics. The main essence of the essence of the spectral method is the replacement of the original differential equations in partial proizodnyh on ordinary diffura for the coefficients of the expansion of the desired functions in a certain basis. The basis can be sine-cosines, complex exponentials, orthogonal polynomials, if geometry requires - cylindrical or spherical functions. The coefficients found at each time point allow you to restore the desired solution, and the FFT algorithm allows you to do this quickly.
The advantages of the method are:
Disadvantages are also available:
I hope my first article will be useful to someone, at least this is a possible start for the students of this section of numerical methods. I look forward to criticism of the code , design and tips!

One-dimensional problem of heat propagation along the rod
First, consider the simple one-dimensional problem of heat distribution in the rod. The equation describing the distribution of heat at some initial temperature distribution over the rod:
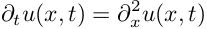
')
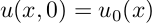
Such an equation is solved analytically by the method of separation of variables, for example, here , but we are interested in how this can be done numerically. First of all, you need to decide how to calculate the second spatial derivative with respect to x. The easiest way to do this is by some difference method, for example:

But we will do otherwise. The temperature distribution is a function of the coordinate and time, and at each moment of time this function can be represented as the sum of the Fourier series, which is numerically truncated on the nth term:

Where u ^ "with a cap" is the decomposition coefficient of a Fourier series. Substitute the expression for the series in the equation of heat transfer:
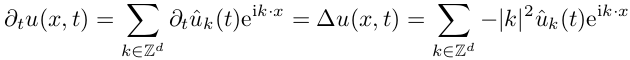
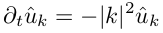
We obtain the equation for the Fourier coefficients, in which there is no derivative with respect to the coordinate! Now this is an ordinary differential equation, and not in partial derivatives, which can be solved by a simple difference method. It is already easier, now it remains to find the decomposition coefficients, and the fast Fourier transform (further FFT) will help us a lot with this.
The logic is as follows:
1) at the initial moment of time, a coordinate function is given that describes the temperature distribution over the rod;
2) we divide the rod into a grid of n points;
3) we find the complex Fourier coefficients using the FFT algorithm, we denote the operation as F (u);
4) multiply the obtained coefficients by - | k | 2 , we obtain the Fourier transform of the second derivative. Similarly, one can obtain the Fourier transform of a derivative of higher orders of p, it is sufficient to multiply by (ik) p ;
5) we do the inverse Fourier transform F -1 (u), using the IFFT algorithm, we obtain the values of the second derivative at points on the grid;
6) make a step in time, already an ordinary difference, explicit or implicit, scheme;
7) repeat.
We now consider how it works in the program for Matlab / Octave. As the initial temperature distribution, we take the smooth function u0 = 2 + sin (x) + sin (2x), split the rod of length 2π into 50 points, with a time step h = 0.1, the boundary conditions are periodic (ring).
Code for the one-dimensional heat transfer equation
clear all; n = 50; % number of points dx = 2*pi/n; % space step x = 0:dx:2*pi-dx; % grid h = 0.1; % temporal step times = 10; % number of iterations in time k = fftshift(-n/2:1:n/2-1); % wave numbers k2 = k.*k; u0 = 2 + sin(x) + sin(2*x); % initial conditions u = zeros(times,n); % stores results u(1,:) = u0; uf = fft(u0); % Fourier coefficients of initial function for i=2:times uf = uf.*(1-h*k2); % next time step in Fourier space u(i,:) = real(ifft(uf)); % IFFT to physical space end [X,T] = meshgrid(x,0:h:times*hh); waterfall(X,T,u) It is worth noting a feature of the FFT algorithm in Matlab, which is related to the fact that the resulting expansion coefficients at the output d = fft (u) do not go in order, but are displaced, the first half in place of the second and vice versa. At first, there are coefficients with numbers from 0 to n / 2-1, then with numbers from -n / 2 to -1. There were problems with it ...
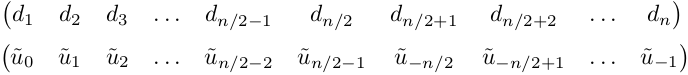
The resulting solution can be seen on the graph as a “waterfall” of temperature distribution lines in x for each time point t. It is seen that the solution undergoes

2D diffusion equation
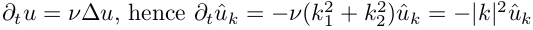
The initial conditions are: u0 = 1 + sin (2X) + cos (2Y), where u is now a 2d array u (i, j). We use an implicit time integration scheme (that is, we express m + 1 step in mth):
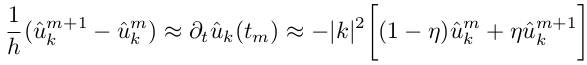
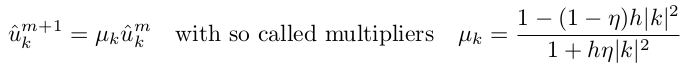
It can be proved that such an implicit scheme never diverges at η> 0.5; we will use η = 1. Thus, each new value of u m + 1 is obtained by multiplying u m by the coefficient μ k , depending on the time step and the wave numbers k, i.e. μ k is a constant that does not need to be recalculated at each step!
Code for the two-dimensional diffusion equation
clear all; eta = 1; n = 32; % number of points dx = 2*pi/n; % space step x = 0:dx:2*pi-dx; y = x; [X, Y] = meshgrid(x,y); h = 0.01; % temporal step times = 30; % number of iterations in time k1 = meshgrid(fftshift(-n/2:1:n/2-1),ones(n,1)); k2 = k1'; ks = k1.*k1 + k2.*k2; mu = (1-(1-eta)*ks^2*h)./(1+eta*ks.^2*h); % stores multipliers u0 = 1 + sin(2*X) + sin(2*Y); % initial temperature u = zeros(times,n,n); % stores results umin=min(min(u0)); umax=max(max(u0)); u(1,:,:) = u0; uf = fft2(u0); for i=2:times uf = mu.*uf; % time step u(i,:,:) = real(ifft2(uf)); end createGif('diffusion2d.gif',X,Y,u,times,1,[0 2*pi 0 2*pi umin umax]); Preservation gifki
function createGif(name,X,Y,u,times,every,ax) % creates gif movie form 3D array % save results to gif file gifka = name; clf; pic = surf(X,Y,squeeze(u(1,:,:))),axis(ax); for i=1:every:times set(pic,'zdata',squeeze(u(i,:,:))), drawnow; M(i) = getframe; frame = getframe; im = frame2im(frame); [imind,cm] = rgb2ind(im,256); if i == 1; imwrite(imind,cm,gifka,'gif','Loopcount',inf); else imwrite(imind,cm,gifka,'gif','WriteMode','append','DelayTime',.1); end end end 
Two-dimensional wave equation

There is a second time derivative in the wave equation, so the task is reduced to a system of two ordinary diffuros, one variable is u, the second is u t , the time scheme in the code used the simplest explicit, so the accuracy is small, the time step is very small, but the code looks relatively simple. However, this is enough to demonstrate the efficiency of the method.
Code for two-dimensional wave equation
clear all; a = 1; % speed of wave propagation n = 64; % number of points dx = 2*pi/n; % space step x = 0:dx:2*pi-dx; y = x; [X, Y] = meshgrid(x,y); h = 0.01; % temporal step times = 1000; % number of iterations in time % explanation of this part is here www.staff.uni-oldenburg.de/hannes.uecker/pre/030-mcs-hu.pdf k1 = meshgrid(fftshift(-n/2:1:n/2-1),ones(n,1)); k2 = k1'; ks = k1.*k1 + k2.*k2; u0 = exp(-100*((X-pi).^2 + (Y-pi).^2)); % profile of initial velocity u ut0 = zeros(n,n); % profile of initial acceleration ut u = zeros(times,n,n); % stores velocity profile for every time steps u(1,:,:) = u0; uf = fft2(u0); uft = fft2(ut0); for i=2:times uft_new = uft - a*h*ks.*uf; uf = uf + 0.5*h*(uft+uft_new); uft = uft_new; % == fixed boundary conditions % u0 = real(ifft2(uf)); % u0(1,:) = 0; u0(end,:) = 0; % u0(:,1) = 0; u0(:,end) = 0; % uf = fft2(u0); % == fixed boundary conditions u(i,:,:) = real(ifft2(uf)); end createGif('wave2d_periodic_bc.gif',X,Y,u,times,10,[0 2*pi 0 2*pi -.2 .2]); Periodic boundary conditions:

Fixed boundary conditions (0 at the edges, reflection of waves from the boundaries):

findings
The article demonstrates several examples of the application of the spectral method for simple problems of mathematical physics. The main essence of the essence of the spectral method is the replacement of the original differential equations in partial proizodnyh on ordinary diffura for the coefficients of the expansion of the desired functions in a certain basis. The basis can be sine-cosines, complex exponentials, orthogonal polynomials, if geometry requires - cylindrical or spherical functions. The coefficients found at each time point allow you to restore the desired solution, and the FFT algorithm allows you to do this quickly.
The advantages of the method are:
- Good accuracy for "good" functions. With an increase in the number of grid points n, the error of the finite-difference method falls as O (N -m )) (where m is some constant that depends on the order of the method and the smoothness of the function), and for the spectral method the accuracy can be exponential O (c N ), where 0 <c <1.
- The relative ease of use, especially when finding derivatives of high degrees, for comparison, the finite difference method involves the use of rather complex formulas. The use of an effective FFT algorithm results in O (N log (N)) complexity, which is acceptable for large enough tasks.
- The spectral method is effective in terms of memory, therefore it is widely used in geophysics, climate modeling and meteorology.
Disadvantages are also available:
- The Gibbs Phenomenon is a very bad phenomenon, strongly influencing the accuracy at the edges of the area.
- More demanding of computing resources for the degree of freedom than in difference methods
- Poorly applicable to problems with non-standard geometry, and boundary conditions other than periodic ones.
I hope my first article will be useful to someone, at least this is a possible start for the students of this section of numerical methods. I look forward to criticism of the code , design and tips!
Used sources
- Excellent review by Hannes Uecker with code examples , some of which I used in this article.
- A small, and therefore wonderful book by Lloyd N. Trefethen, Spectral Methods in MATLAB
- The fundamental book of John P.Boyd "Chebyshev and Fourier Spectral Methods"
Source: https://habr.com/ru/post/267401/
All Articles