RC5 encryption algorithm and its implementation in python

RC5 algorithm
In my post, I would like to talk about the RC5 symmetric encryption algorithm and my version of its implementation in python. This algorithm was developed by the most famous cryptologist Ronald
Introduction
In the description of the algorithm we will use the following notation:
- Word size
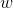 in bits . RC5 encrypts in two word blocks; valid values are 16, 32, and 64. This value is recommended to be taken equal to the machine word. For example for 32-bit machines
in bits . RC5 encrypts in two word blocks; valid values are 16, 32, and 64. This value is recommended to be taken equal to the machine word. For example for 32-bit machines 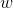 = 32 and therefore the block size will be 64 bits
= 32 and therefore the block size will be 64 bits - The number of rounds of the algorithm
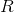 - integer from 0 to 255 inclusive. If set to 0, encryption will not be performed.
- integer from 0 to 255 inclusive. If set to 0, encryption will not be performed. - Secret key size
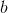 in bytes - an integer from 0 to 255 inclusive
in bytes - an integer from 0 to 255 inclusive
To clarify the parameters used in a particular case, the notation RC5- is used.
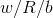 ;
;for example, RC5-32 / 12/16 denotes the RC5 algorithm with a 64-bit block, 12 rounds of encryption and a 16-byte key (this combination is recommended by Rivest as the main option).
The work of the algorithm consists of two stages:
- Key Expansion Procedure
- Encryption itself
Create a class and constructor initializing the necessary starting variables.
Python listing
def __init__(self, w, R, key): self.w = w self.R = R self.key = key self.T = 2 * (R + 1) self.w4 = w // 4 self.w8 = w // 8 self.mod = 2 ** self.w self.mask = self.mod - 1 self.b = len(key) self.__keyAlign() self.__keyExtend() self.__shuffle() Key Expansion Procedure
I propose to start with a stage that is a little more complicated, namely, with the key expansion procedure. For this we need to write 3 simple functions:
- Key alignment
- Extended key array initialization
- Shuffle arrays of keys
Key alignment
If the key size (in bytes) is not a multiple
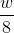 , we supplement it with zero bytes to the nearest multiple
, we supplement it with zero bytes to the nearest multiple 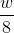 . After that, the key is copied to the array.
. After that, the key is copied to the array. ![L [0] .. L [c]](https://habrastorage.org/files/3d2/fae/eae/3d2faeeae4234504a669f0e335f87a0a.gif) where
where 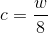 . Simply put, we copy the key in blocks of
. Simply put, we copy the key in blocks of 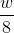 bytes (2, 4, 8 for values
bytes (2, 4, 8 for values 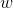 16, 32, 64 respectively) into an array
16, 32, 64 respectively) into an array 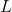 .
.For example, with parameters
 and key value
and key value 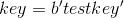 we'll get
we'll get ![L [0] = b'test](https://habrastorage.org/files/45c/8f0/f76/45c8f0f7688347c0b903e4077dffa2a9.gif) and
and ![L [1] = b'key \ x00](https://habrastorage.org/files/62b/7c5/44c/62b7c544cee84108952cda1d41c449ef.gif) (0 means zero byte).
(0 means zero byte).We describe the necessary function
Python listing
def __keyAlign(self): if self.b == 0: # self.c = 1 elif self.b % self.w8: # w / 8 self.key += b'\x00' * (self.w8 - self.b % self.w8) # \x00 self.b = len(self.key) self.c = self.b // self.w8 else: self.c = self.b // self.w8 L = [0] * self.c for i in range(self.b - 1, -1, -1): # L L[i // self.w8] = (L[i // self.w8] << 8) + self.key[i] self.L = L Initialization of the extended key array
In this step, we need to generate pseudo-random constants.
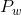 and
and 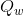 according to the following formulas:
according to the following formulas: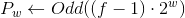
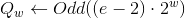 ,
,Where
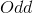 - rounding function to the nearest inappropriate
- rounding function to the nearest inappropriate - Euler number
- Euler number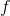 - golden ratio
- golden ratio')
Also in the specification of the algorithm are already calculated constants for all possible values.
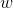 :
: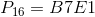
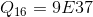
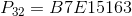
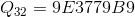
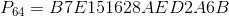
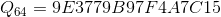 ,
,all constants are represented in hexadecimal.
Having got everything we need, we initialize the array.
![S [0] .. S [2 * r + 1]](https://habrastorage.org/files/14c/031/840/14c0318409954c5299dfb5d47f23963f.gif) where
where![S [0] = Pw](https://habrastorage.org/files/412/214/c3b/412214c3bc3346a2a1a93a62eb4257ed.gif)
![S [i + 1] = S [i] + Qw](https://habrastorage.org/files/8ba/b2a/76e/8bab2a76ef2c417f8f640af2c57e0180.gif)
Feature Description
Python listing
def __const(self): # if self.W == 16: return (0xB7E1, 0x9E37) # P Q elif self.W == 32: return (0xB7E15163, 0x9E3779B9) elif self.W == 64: return (0xB7E151628AED2A6B, 0x9E3779B97F4A7C15) def __keyExtend(self): # S P, Q = self.__const() self.S = [(P + i * Q) % self.mod for i in range(self.T)] Stirring
Now, before proceeding to encryption, we need only mix the elements of the arrays L and S by executing the following cycle:
![A = S [i] = (S [i] + A + A) <<< 3](https://habrastorage.org/files/2c3/679/2ab/2c36792abd0643d0993a70bbbecba30c.gif)
![B = L [j] = (L [j] + A + B) <<< (A + B)](https://habrastorage.org/files/5eb/110/1f6/5eb1101f6b844bd689f89e7b59b6796d.gif)
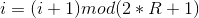
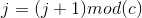 where
where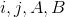 - temporary variables, initial values are 0
- temporary variables, initial values are 0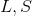 - arrays obtained in the previous steps
- arrays obtained in the previous stepsNumber of iterations
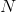 defined as
defined as 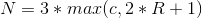
Python listing
Lshift and rshift (which we will meet below) are logical left and right operations, respectively.
I think that their comments will be redundant, and the code can be viewed on github (link at the end)
def __shuffle(self): i, j, A, B = 0, 0, 0, 0 for k in range(3 * max(self.c, self.T)): A = self.S[i] = self.__lshift((self.S[i] + A + B), 3) B = self.L[j] = self.__lshift((self.L[j] + A + B), A + B) i = (i + 1) % self.T j = (j + 1) % self.c Lshift and rshift (which we will meet below) are logical left and right operations, respectively.
I think that their comments will be redundant, and the code can be viewed on github (link at the end)
Algorithm structure
Encryption
The algorithm is a network of its Feistel, in each round of which (with the exception of zero) the following operations are performed:
![A = ((A + B) <<< B) + S [2 * r] mod2 ^ w](https://habrastorage.org/files/062/12e/cda/06212ecda1674f018670146136481463.gif)
![B = ((A + B) <<< A) + S [2 * r + 1] mod2 ^ w](https://habrastorage.org/files/ae2/6e6/f33/ae26e6f3304b4f8dbe25893894c14473.gif) ,
,Where
![S [n]](https://habrastorage.org/files/8f9/c29/383/8f9c29383c5a48c58346a52f3f20b533.gif) - extended key fragment
- extended key fragment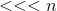 - cyclic shift operation on
- cyclic shift operation on 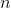 bits left
bits leftIn the zero round, the operations of imposing the first two fragments of the extended key on the encrypted data are performed:
![A = (A + S [0]) mod2 ^ w](https://habrastorage.org/files/3ef/39f/3d0/3ef39f3d0e98473da28752fd8850aa44.gif)
![B = (B + S [1]) mod2 ^ w](https://habrastorage.org/files/57f/7b1/a8f/57f7b1a8f3e8495ea9de91b0467b94ff.gif)
It is worth noting that a round means transformations, corresponding to two rounds of conventional algorithms designed on the basis of Feistel networks. For a round, RC5 processes the block as a whole, in contrast to the round of the Feistel network processing one sub-block - most often half of the block.
Corresponding code:
Python listing
def encryptBlock(self, data): A = int.from_bytes(data[:self.w8], byteorder='little') B = int.from_bytes(data[self.w8:], byteorder='little') A = (A + self.S[0]) % self.mod B = (B + self.S[1]) % self.mod for i in range(1, self.R + 1): A = (self.__lshift((A ^ B), B) + self.S[2 * i]) % self.mod B = (self.__lshift((A ^ B), A) + self.S[2 * i + 1]) % self.mod return (A.to_bytes(self.w8, byteorder='little') def encryptFile(self, inpFileName, outFileName): # with open(inpFileName, 'rb') as inp, open(outFileName, 'wb') as out: run = True while run: text = inp.read(self.w4) if not text: break if len(text) != self.w4: text = text.ljust(self.w4, b'\x00') # , , run = False text = self.encryptBlock(text) out.write(text) Decryption
Data decryption is performed by applying the inverse operation in reverse order We first perform the following cycle:
![B = (((B-S [2 * r + 1]) mod2 ^ w) >>> A) + A](https://habrastorage.org/files/255/df6/edb/255df6edbdd24c7ab507969c618719d2.gif)
![A = (((A-S [2 * r]) mod2 ^ w) >>> B) + B](https://habrastorage.org/files/e50/a47/9e5/e50a479e53de4dffaaefaa941f9f629f.gif) ,
,Where
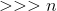 - cyclic right shift operation
- cyclic right shift operation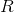 and ending with a unit.
and ending with a unit.After this, the operations are reverse for the zero round, namely:
![B = (B-S [1]) mod2 ^ w](https://habrastorage.org/files/b57/61d/ab0/b5761dab08b54b67b8e1cad5c2432b4c.gif)
![A = (A-S [0]) mod2 ^ w](https://habrastorage.org/files/2b2/755/9df/2b27559df7cf4e839ab3200800381b59.gif)
Code here:
Python listing
def decryptBlock(self, data): A = int.from_bytes(data[:self.w8], byteorder='little') B = int.from_bytes(data[self.w8:], byteorder='little') for i in range(self.R, 0, -1): B = self.__rshift(B - self.S[2 * i + 1], A) ^ A A = self.__rshift(A - self.S[2 * i], B) ^ B B = (B - self.S[1]) % self.mod A = (A - self.S[0]) % self.mod return (A.to_bytes(self.w8, byteorder='little') + B.to_bytes(self.w8, byteorder='little')) def decryptFile(self, inpFileName, outFileName): with open(inpFileName, 'rb') as inp, open(outFileName, 'wb') as out: run = True while run: text = inp.read(self.w4) if not text: break if len(text) != self.w4: run = False text = self.decryptBlock(text) if not run: text = text.rstrip(b'\x00') # b'\x00' out.write(text) The algorithm is strikingly simple - it uses only modulo 2 and modulo addition operations.
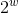 as well as shifts by a variable number of bits. The last of the operations is presented by the author of the algorithm as a revolutionary solution that was not used in earlier encryption algorithms (prior to the RC5 algorithm, these were used only in the Madryga algorithm, which was not widely used) - a shift by a variable number of bits is a very simple operation, but significantly complicates the differential and linear cryptanalysis of the algorithm. The simplicity of the algorithm can be considered as its important advantage - a simple algorithm is easier to implement and easier to analyze for possible vulnerabilities.
as well as shifts by a variable number of bits. The last of the operations is presented by the author of the algorithm as a revolutionary solution that was not used in earlier encryption algorithms (prior to the RC5 algorithm, these were used only in the Madryga algorithm, which was not widely used) - a shift by a variable number of bits is a very simple operation, but significantly complicates the differential and linear cryptanalysis of the algorithm. The simplicity of the algorithm can be considered as its important advantage - a simple algorithm is easier to implement and easier to analyze for possible vulnerabilities.The whole code can be viewed on github .
Bit of cryptanalysis
- There is a class of keys using which the algorithm can be opened by linear cryptanalysis. In other cases it is almost impossible.
- Differential cryptanalysis is more effective when attacking this algorithm. For example, for the algorithm RC5-32-12-16, at best, it is required
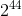 selected clear texts for a successful attack. When using 18-20 (and more) rounds instead of 12, it is almost impossible to open the algorithm using differential cryptanalysis.
selected clear texts for a successful attack. When using 18-20 (and more) rounds instead of 12, it is almost impossible to open the algorithm using differential cryptanalysis.
Thus, the most realistic method of cracking the RC5 algorithm (not counting the options with a small number of rounds and with a short key) is a complete search through the possible options for the encryption key. Which means that the RC5 algorithm has practically no flaws in terms of its durability. On this and I would like to finish. Thank you all for your attention.
UPD: Changed operation lshift, rshift. Added constants to the class constructor. Added tests.
Thank you mas for advice and help.
Source: https://habr.com/ru/post/267295/
All Articles