Hash array mapped trie
Hash array mapped trie is an associative container that has hash table and trie properties. Key-value pair insertion and key search operations are O (1) operations.
About trie on Habré already wrote .
')
Strings are often stored in trie, so there is a concept of an alphabet from which elements can be composed. To optimize for x32 limit the size of the alphabet to 32 (0 - 31).
Let's see what array mapped trie looks like, it’s AMT (taken from [1]):

AMT consists of a node and several segments connecting our node and other nodes. Each segment is one of the possible symbols of the alphabet.
The node contains a 32-bit structure (bitmap), each bit of the structure reflects the state of one of the 32 segments (0 - no, 1 - is). Also in the node is a table in which pointers to subtrees or the last characters in a given substring (leaves) are stored. The pointers in the table are stored in order, and each of the pointers corresponds to a bit = 1 in the bit structure.
Example: to find the character 's', you must go through the bit structure to the corresponding bit. While we are going according to the structure, we count bits = 1 (cocked bits). Suppose we counted 5 cocked bits, and the bit corresponding to 's' turned out to be the 6th cocked bit. Accordingly, we need the 6th pointer in the table of this node. If the bit is not entered (= 0), then this symbol is not.
We now turn to HAMT . The upper bits of the hash are used instead of the alphabet. This is what HAMT looks like (taken from [1]):
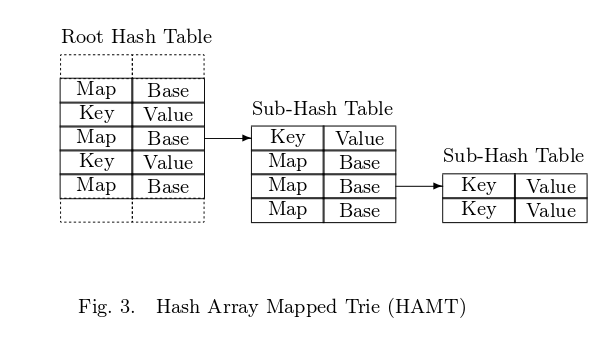
HAMT consists of a main hash table of size 2 ^ t, where usually t> = 5. Each element of the main table:
1. either the root node of the sub-table tree with a size of 32
2. either just a pair of key - value
The choice of hash function depends on your data set. It is advisable to choose a hash function that gives the minimum number of collisions (for more details about collisions in [2]).
1. Generate a 32-bit hash for the key.
2. From the resulting hash, we take t high bits (note: we take t high bits only for the first time, the rest - 5 bits each) and use them as an index in the table. There are 3 possible options:
a) there is nothing in the cell with such an index — there is no such key in the table;
b) there is one key / value pair in the cell. If the key matched - found the item, did not match - did not find;
c) a 32-bit bitmap and a table with pointers are stored in the cell. In this case, take the next 5 bits of the hash and use them again as an index in the bitmap. If the bit is not cocked, then there is no such key; if it is cocked, then we count all the coded bits from the beginning to the current (as in AMT). So we got the number of the required pointer in the table. Follow the pointer and repeat the algorithm.
Often, only a few iterations of this algorithm are needed (although this depends on the fullness of the tree). The key is compared only once - when we are in a situation b. The lack of a key is also detected early enough.
Repeat the steps from the insertion algorithms until one of 3 situations occurs:
a) there is nothing in the cell with such an index;
b) a 32-bit bitmap and a table with pointers are stored in the cell;
In both cases, the algorithms are simple: if the insertion occurs in the main table, then simply insert the key / value pair. If the insertion occurs in a sub-table, then we coax the corresponding bit, allocate a new table of pointers, copy into it pointers from the old table and a new pointer to our pair, and delete the old table.
As a result, we have set the bit of the corresponding cell, in the pointer table all the old pointers, and also in the corresponding cell the new pointer.
c) a collision occurred - i.e., some part of the two hashes coincided with us. The solution is simple - we create a new sub-table, from the existing key we calculate the hash and use the next 5 bits to find the desired cell. We tap the bit in this cell, insert into the pointer table the pointer to the existing key / value pair, go back to the pair to be inserted, take the next 5 bits too, and look for the desired cell. This step with the creation of a new subdatasheet is repeated until the collision disappears.
With each such step, the probability of a collision decreases 32 times (the size of the table of pointers and bitmap).
Sometimes we get a complete collision - all 32 bits of hashes of two different keys are the same. Then we take the following hash function and hash it with two conflicting keys. As a result, when we search for the key element - we go through all the bits of the primary hash, we see that we did not come to the list, but to the subtable, and calculate the new hash of the key using the second function.
In general, this is not the only way to solve collisions, there are others in different implementations. In his work, the author proposes to use the same hash function, simply after a collision, to give her the key and the level of the tree in which we are at this step of the algorithm (0 - root table, etc.). If an application is critically important that the insert operation time is limited from above (theoretically, we can take two such keys, that their hashes will coincide after several calls to the rehash function, which means that the insert operation will take a very long time), then instead of rehashing the matching keys you can use the keys themselves.
We need pools from 1 to 32 elements (for tables of various sizes). Select the memory blocks and divide them into the corresponding tables. In the process of work, the fragmentation will gradually increase. In order to return the memory, it is necessary to defragment. You can set a limit on the amount of fragmented memory in percent, check it when inserting an element and when it exceeds the limit - defragment it. The defragmentation operation can be implemented as an O (1) operation.
At some point, the tree will grow so much that increasing the size of the root table will give a noticeable increase in speed. Each subtable has 32 elements, so the change from 2 ^ t to 2 ^ (t + 5) will be the most logical. When increasing the size, all sub-tables of the first level fall into the root table. Moreover, reheshirovanie need only in the case when we have in the root table fall leaves of the tree (you need to re-calculate the hash to determine the new position of the element). In other cases, simply copy the elements from the subtable into the root table.
It is possible not to immediately copy all the subtables into the root table, but gradually. In this case, the transfer index is memorized. All items below the index are copied to the new table, and the index gradually moves up the old table. During the search, the first t bits of the hash are compared with the transfer index — if the hash is greater, the search is directed to the old table, otherwise to the new one. The insertion algorithm must also take into account the transfer index.
When should I increase the root table? When the size of the new table will occupy 1 / f from the entire tree. The parameter f must be selected based on the specific situation.
The amount of memory depends on the transfer index. The author in his work gave a table showing this dependence (taken from [1])
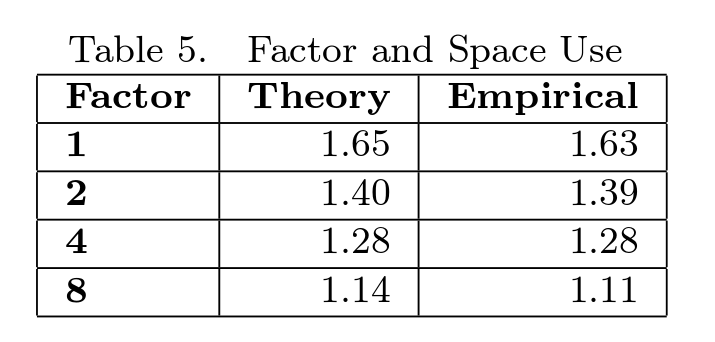
That is, if the transfer index = N / 4, where N is the number of key-value pairs inserted into the tree, then the occupied memory is proportional to 1.28 * N.
During removal, two situations can occur:
a) delete the element in the sub-table with the number of elements greater than 2. Then you need to move all other elements to a smaller sub-table, and mark the current one as empty.
b) delete the element in the subtable with the number of elements equal to 2. In this situation, the remaining element is simply transferred to the subtable a higher level, and the current one is marked empty.
I lost the link to the implementation from the author in C ((Who will find - write in the comment.
github.com/yasm/yasm/blob/master/libyasm/hamt.c is an example implementation in C. References to examples of implementation in other languages can be found in [3].
[1] article from the author of the algorithm
[2] article about hash collisions on Wikipedia
[3] HAMT article on Wikipedia
[4] good question on SO
[5] short introductory course in HAMT
Write comments and inaccuracies in the comments, send spelling errors and lost punctuation marks to the PM.
About trie on Habré already wrote .
Structure array mapped trie
')
Strings are often stored in trie, so there is a concept of an alphabet from which elements can be composed. To optimize for x32 limit the size of the alphabet to 32 (0 - 31).
Let's see what array mapped trie looks like, it’s AMT (taken from [1]):

AMT consists of a node and several segments connecting our node and other nodes. Each segment is one of the possible symbols of the alphabet.
The node contains a 32-bit structure (bitmap), each bit of the structure reflects the state of one of the 32 segments (0 - no, 1 - is). Also in the node is a table in which pointers to subtrees or the last characters in a given substring (leaves) are stored. The pointers in the table are stored in order, and each of the pointers corresponds to a bit = 1 in the bit structure.
Example: to find the character 's', you must go through the bit structure to the corresponding bit. While we are going according to the structure, we count bits = 1 (cocked bits). Suppose we counted 5 cocked bits, and the bit corresponding to 's' turned out to be the 6th cocked bit. Accordingly, we need the 6th pointer in the table of this node. If the bit is not entered (= 0), then this symbol is not.
Structure hash array mapped trie
We now turn to HAMT . The upper bits of the hash are used instead of the alphabet. This is what HAMT looks like (taken from [1]):

HAMT consists of a main hash table of size 2 ^ t, where usually t> = 5. Each element of the main table:
1. either the root node of the sub-table tree with a size of 32
Index Node: int bitmap (32 bits) Node*[] table (max length of 32) 2. either just a pair of key - value
Key Value Node: K key V value The choice of hash function depends on your data set. It is advisable to choose a hash function that gives the minimum number of collisions (for more details about collisions in [2]).
Item Search
1. Generate a 32-bit hash for the key.
2. From the resulting hash, we take t high bits (note: we take t high bits only for the first time, the rest - 5 bits each) and use them as an index in the table. There are 3 possible options:
a) there is nothing in the cell with such an index — there is no such key in the table;
b) there is one key / value pair in the cell. If the key matched - found the item, did not match - did not find;
c) a 32-bit bitmap and a table with pointers are stored in the cell. In this case, take the next 5 bits of the hash and use them again as an index in the bitmap. If the bit is not cocked, then there is no such key; if it is cocked, then we count all the coded bits from the beginning to the current (as in AMT). So we got the number of the required pointer in the table. Follow the pointer and repeat the algorithm.
Often, only a few iterations of this algorithm are needed (although this depends on the fullness of the tree). The key is compared only once - when we are in a situation b. The lack of a key is also detected early enough.
Insert item
Repeat the steps from the insertion algorithms until one of 3 situations occurs:
a) there is nothing in the cell with such an index;
b) a 32-bit bitmap and a table with pointers are stored in the cell;
In both cases, the algorithms are simple: if the insertion occurs in the main table, then simply insert the key / value pair. If the insertion occurs in a sub-table, then we coax the corresponding bit, allocate a new table of pointers, copy into it pointers from the old table and a new pointer to our pair, and delete the old table.
As a result, we have set the bit of the corresponding cell, in the pointer table all the old pointers, and also in the corresponding cell the new pointer.
c) a collision occurred - i.e., some part of the two hashes coincided with us. The solution is simple - we create a new sub-table, from the existing key we calculate the hash and use the next 5 bits to find the desired cell. We tap the bit in this cell, insert into the pointer table the pointer to the existing key / value pair, go back to the pair to be inserted, take the next 5 bits too, and look for the desired cell. This step with the creation of a new subdatasheet is repeated until the collision disappears.
With each such step, the probability of a collision decreases 32 times (the size of the table of pointers and bitmap).
Sometimes we get a complete collision - all 32 bits of hashes of two different keys are the same. Then we take the following hash function and hash it with two conflicting keys. As a result, when we search for the key element - we go through all the bits of the primary hash, we see that we did not come to the list, but to the subtable, and calculate the new hash of the key using the second function.
In general, this is not the only way to solve collisions, there are others in different implementations. In his work, the author proposes to use the same hash function, simply after a collision, to give her the key and the level of the tree in which we are at this step of the algorithm (0 - root table, etc.). If an application is critically important that the insert operation time is limited from above (theoretically, we can take two such keys, that their hashes will coincide after several calls to the rehash function, which means that the insert operation will take a very long time), then instead of rehashing the matching keys you can use the keys themselves.
Memory allocation
We need pools from 1 to 32 elements (for tables of various sizes). Select the memory blocks and divide them into the corresponding tables. In the process of work, the fragmentation will gradually increase. In order to return the memory, it is necessary to defragment. You can set a limit on the amount of fragmented memory in percent, check it when inserting an element and when it exceeds the limit - defragment it. The defragmentation operation can be implemented as an O (1) operation.
Resize root table
At some point, the tree will grow so much that increasing the size of the root table will give a noticeable increase in speed. Each subtable has 32 elements, so the change from 2 ^ t to 2 ^ (t + 5) will be the most logical. When increasing the size, all sub-tables of the first level fall into the root table. Moreover, reheshirovanie need only in the case when we have in the root table fall leaves of the tree (you need to re-calculate the hash to determine the new position of the element). In other cases, simply copy the elements from the subtable into the root table.
It is possible not to immediately copy all the subtables into the root table, but gradually. In this case, the transfer index is memorized. All items below the index are copied to the new table, and the index gradually moves up the old table. During the search, the first t bits of the hash are compared with the transfer index — if the hash is greater, the search is directed to the old table, otherwise to the new one. The insertion algorithm must also take into account the transfer index.
When should I increase the root table? When the size of the new table will occupy 1 / f from the entire tree. The parameter f must be selected based on the specific situation.
Memory required
The amount of memory depends on the transfer index. The author in his work gave a table showing this dependence (taken from [1])

That is, if the transfer index = N / 4, where N is the number of key-value pairs inserted into the tree, then the occupied memory is proportional to 1.28 * N.
Remove item
During removal, two situations can occur:
a) delete the element in the sub-table with the number of elements greater than 2. Then you need to move all other elements to a smaller sub-table, and mark the current one as empty.
b) delete the element in the subtable with the number of elements equal to 2. In this situation, the remaining element is simply transferred to the subtable a higher level, and the current one is marked empty.
Source
I lost the link to the implementation from the author in C ((Who will find - write in the comment.
github.com/yasm/yasm/blob/master/libyasm/hamt.c is an example implementation in C. References to examples of implementation in other languages can be found in [3].
Links
[1] article from the author of the algorithm
[2] article about hash collisions on Wikipedia
[3] HAMT article on Wikipedia
[4] good question on SO
[5] short introductory course in HAMT
Write comments and inaccuracies in the comments, send spelling errors and lost punctuation marks to the PM.
Source: https://habr.com/ru/post/266861/
All Articles