Geekly Articles each Day
📜 ⬆️ ⬇️

Non-intersecting sets and mysterious function of Ackermann

It will be a simple data structure - a system of disjoint sets . Briefly: non-intersecting sets are given (for example, connected components of a graph) and by two elements x and y you can: 1) find out whether x and y are in the same set; 2) combine the sets containing x and y. The structure itself is very simple to implement and has been described many times in various places (for example, there is a good article on Habré and elsewhere). But this is one of those amazing algorithms that doesn't cost anything to write, but it’s hard to figure out why it works effectively. I will try to present a relatively simple proof of the exact estimate for the time of operation of this data structure, invented by Zeydel and Sharir in 2005 (it is different from the horror that many could see elsewhere). Of course, the structure itself will also be described, and along the way we will understand, and here the inverse function of Akkerman, which many people only know about, is sooooo slowly growing.

The system of disjoint sets


Imagine that for some reason you had to maintain a set of n points with two queries: Union (x, y), which connects the points x and y with an edge, and IsConnected (x, y), which checks the points x and y is it possible to pass from x along the edges to y. How to solve this problem?

First, it is reasonable to think not about points, but about connected components. A connected component is a set of points in which from each point one can go along the edges to each other of the same set. Then Union (x, y) is simply a union of components containing x and y (if they are not in the same component), and IsConnected (x, y) is a test of whether x and y are in the same component.

Secondly, it is convenient to select in each component one particular selected vertex taken at random. Let Find (x) return the selected vertex from the component containing x. Using Find (x), the IsConnected (x, y) function reduces to a simple comparison of Find (x) and Find (y): IsConnected (x, y) == (Find (x) == Find (y)). When two components are merged into one with Union, the selected vertex of one of the merged components ceases to be selected, because the selected vertex in one component is always the same.
')
So, we abstract away from the original problem and reduce it to solving another, more general task: we have a set of non-intersecting sets that can be combined with Union and have a dedicated element obtained using Find. Formally, the structure can be described as follows: there is an initial set of singleton sets {x 1 }, {x 2 }, ..., {x n } with such operations:


Systems of non-intersecting sets, or rather, their implementation about which will be discussed further, were invented at the dawn of computer science. Sometimes this structure is called Union-Find. Systems of non-intersecting sets have many applications: they play a central role in the Kraskal algorithm for finding the minimum skeleton, are used in building the so-called dominator tree (a natural thing when analyzing a code), make it easy to monitor connectivity components in a graph, etc. I’ll say right away, even though this article contains a brief description of the implementation of the very structure of disjoint sets, for a detailed discussion of the applications of these structures and implementation details, it is better to read the already cited sources in Habré and in Maxim Ivanov . But it was always interesting to me to find out how that unusual estimate for the operating time of the systems of non-intersecting sets is obtained, which is not even easy to understand. So, the main goal of this article is the theoretical substantiation of the effectiveness of the Union-Find structures.

How to implement sets with Union-Find operations? The first thing that comes to mind is to store sets in the form of directed trees (see figure). Every tree is a multitude. The selected element of the set (the one that the Find function returns) is the root of the tree. To merge trees, you just need to attach the root of one tree to another.



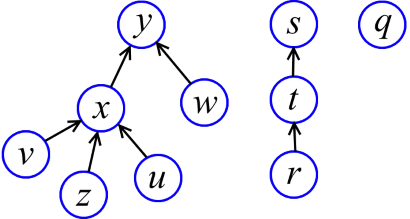
Find (x) simply goes up from x along the arrows until it reaches the root, and returns the root. But if you leave everything as it is, you will easily get "bad" trees (such as a long "chain"), on which Find spends a lot of time. That is, "high" trees to us to anything.

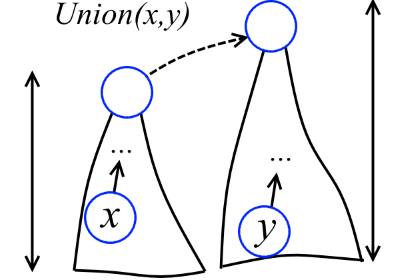
The height of the vertex x is the maximum length of the path from a sheet to x. For example, in the figure above, the height y - 2, x - 1, z - 0. After some thought, you can provide each vertex with a height. We will call these heights ranks (looking ahead, I will say that these things are not called heights, as expected, because in the future the trees will be rearranged and the ranks will no longer exactly match the heights). Now, when two trees are combined, the lower tree will be picked up to the higher one (see the figure below).



We realize it! Nodes-elements are defined as:

struct elem { elem *link; //    int rank; //  double value; //-    };

Initially, x.link = 0 and x.rank = 0 is performed for each x element. You can already write a merge function and a preliminary version of the Find function:

 void Union(elem *x, elem *y) { x = Find(x); y = Find(y); if (x != y) { if (x->rank == y->rank) y->rank++; else if (x->rank > y->rank) swap(x, y); x->link = y; } } elem *Find(elem *x) //   Find { return x->link ? Find(x->link) : x; }

Even this implementation is already quite effective. To see this, we prove a couple of simple lemmas.

Lemma 1. In the Union-Find implementation with rank optimization, each tree with the root x contains ≥2 x-> rank vertices.

Evidence. For trees consisting of one vertex x, x-> rank = 0 and it is clear that the statement of the lemma is fulfilled. Let Union join trees with roots x and y, for which the statement of the lemma holds, that is, trees with roots x and y contain ≥2 x-> rank and ≥2 y-> rank vertices, respectively. A problem may occur if x joins y and the rank of y increases. But this happens only if x-> rank == y-> rank. Let r be the rank of y before the union. Therefore, a new tree with a root y contains ≥2 x-> rank + 2 r = 2 2 r = 2 r + 1 vertices. And this was required to prove.

Lemma 2. In a Union-Find with rank optimization, the rank of each vertex x is equal to the height of the tree with root x.

Evidence. When the algorithm is just starting to work and all the sets are singleton, for each vertex x-> rank = 0, which undoubtedly is the height. Let Union join two trees with roots x and y and let the heights of these trees be exactly equal to the corresponding ranks x-> rank and y-> rank. We show that even after the union, the ranks are equal to the heights. If x-> rank <y-> rank, then x will be hooked to y and, obviously, the height of the tree with the root y will not change; Union doesn't really change y-> rank. The case x-> rank> y-> rank is similar. If x-> rank == y-> rank, then after joining x to y, the height y will increase by one; and Union just increases y-> rank by one. What was required.

From Lemma 1 it follows that the rank of any vertex cannot be greater than log n (all logarithms are base 2), where n denotes the number of elements. And from Lemma 2 it follows that the height of any tree does not exceed log n. This means that each Find operation is performed in O (log n). Therefore, m Union-Find operations are performed in O (m log n).

Is it even more effective? The second optimization comes to the rescue. When performing an ascent in the Find procedure, we simply redirect all the passed vertices to the root (see the figure). Worse from this just will not. But it turns out to be much better.



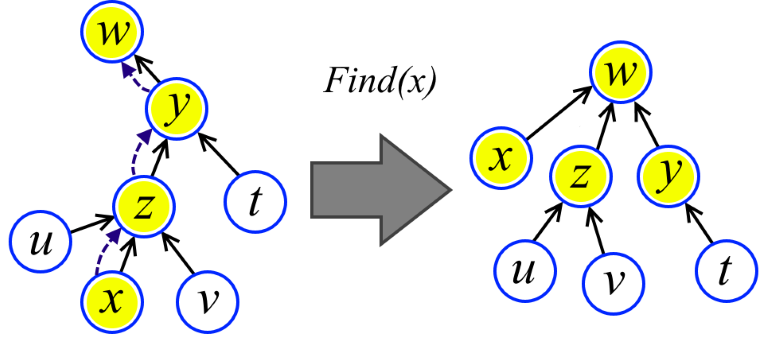
 elem * Find(elem *x) { return x->link ? (x->link = Find(x->link)) : x; }

So, we have a sequence of m operations Union and Find on n elements and we need to estimate how much time it works. Could it be O (m log n)? Or O (m log log n)? Or all the same O (m)?

Intuitively, it seems that the algorithm with the second optimization should be more efficient. And so it is, but to prove it is not so easy. Having a little analyzed, we can assume that the algorithm is linear, i.e. a sequence of m operations Union and Find alternately performed for O (m). But no matter how you try, to prove it strictly will not work, because it is not. The first complete proof of the exact upper and lower bounds was given by Taryan in 1975 and this boundary is “almost” O (m), but, unfortunately, not O (m). Then came work in which it was proved that, in principle, it is impossible to obtain O (m). Honestly, I could not figure out all this; even a counterexample, showing that Union-Find is slower than O (m), is rather difficult to understand. But fortunately, in 2005, Seidel and Sharir received a new relatively “understandable” proof of the upper limit. Their article is called “Top-down analysis of path compression”. It is their result in a little more simplified form that I will try to explain here. Finding "understandable" proof of the lower bound can be considered as an unsolved problem.

Is it so bad that we did not grow together with O (m)? Actually, all this is only of purely theoretical interest, because the “almost” O (m) obtained by Tarjan is indistinguishable from O (m) in all conceivable input data (it will soon become clear why). I’ll say right away that there is no evidence that this is not O (m) (I just don’t quite understand it myself), so one may get the impression that it can be a little more and ... But it is impossible. At least, despite some failed attempts, it was not possible to find critical errors in Taryan’s work and a series of related works. A well-known attempt in the article “The Union-Find Problem is Linear,” according to the author himself, is mistaken, quote: “This paper has an error and has been retracted. It should simply be deleted from Citeseer. Baring that, I am submitting this "correction". ".

Stars, Stars, Stars


What are these functions that give “almost” O (m)? Consider some function f such that f (n) <n for all n> 1, but f (n) tends to infinity. The function f grows slowly: its entire graph is below the graph of the function g (n) = n. We define the iteration operator * , which makes a slow function f * super slow function f * :

f * (n) = min {k: f (f (... f (n))) <2, where f is taken k times}

That is, f * (n) shows how many times it is necessary to compress the number n with the operations f (n)> f (f (n))> f (f (f (n)))> ... to get a constant of less than two.

A couple of examples to get comfortable. If f (n) = n-2, then f * (n) = [n / 2] (the integer part of dividing by two). If f (n) = n / 2, then f * (n) = [log n] (the integer part of the binary logarithm). If f (n) = log n, then what is f * (n) = log * n? The log * n function is called iterated logarithm . Having written a little bit on paper, one can prove that log * n = O (log log n), log * n = O (log log log n) and generally log * n = O (log log ... log n) for any number logs. To imagine how slow the iterated logarithm is, just look at the value of log * 2 65536 = 5.

In the following, it will be shown that the execution time of Union-Find m operations can be estimated as O (m log * n) and, moreover, we can derive the estimates O (m log ** n), O (m log *** n) and so on to some limit function O (m α (m, n)) defined below. In general, I believe that for modern practical applications O (m log log n) is almost indistinguishable from O (m). And O (m log * n) is not at all distinguishable from O (m), what to say about O (m log ** n) and others. Now you can imagine why we are talking about "almost" O (m).

O (m log * n) score


Obtaining an O (m log * n) estimate is the main part of the proof. After that, an exact estimate will be obtained almost immediately. To make it easier, we take one unimportant assumption: m ≥ n.

Without limiting the generality of reasoning, we will assume that the Union operation always takes as its input “roots” of sets, i.e. Union is called like this: Union (Find (x), Find (y)). Then Union is executed for O (1). This restriction is all the more natural, because Union (x, y) is the first thing that calls Find (x) and Find (y). This means that in the analysis we will be interested only in Find operations.

Continue to simplify. Imagine that Find operations are not performed at all and the user somehow guesses where the roots of the sets are. The sequence of the Union-s builds a forest F (forest - a lot of trees). By Lemma 2 in F, the rank of each vertex x is the height of the subtree with root at x. It follows that the rank of each vertex is less than the rank of the parent of this vertex. For us, this observation is important.

Now let's return the Find sequence to the system. One can imagine that the first Find runs along a path in F and performs a path compression operation in F, in which each vertex of the path becomes a scion of the vertex in the “head” of the path (see the figure). In this case, the head of the path is not necessarily the root of F. In other words, let's agree that in a sense, all the Union were executed in advance, and now on the forest F, the paths corresponding to Find are compressed during the normal course of the algorithm. Then the second Find runs along some path already in the modified forest (in the source forest F, this path could not exist at all) and again compresses the path. And so on.

It is important to note that after compression the paths do not change. Therefore, we call ranks, not heights, because in a modified forest, ranks may no longer correspond to heights.



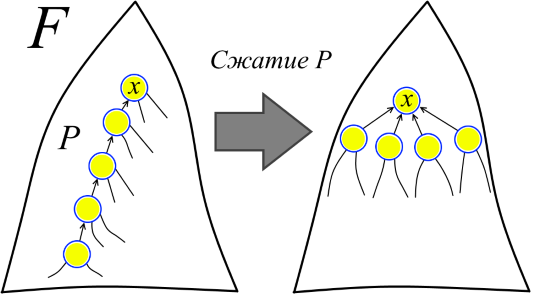
Now we can clearly articulate what we are proving. There is a sequence of forests F = F 1 , F 2 , ..., F m and a sequence of contractions of the paths P 1 , P 2 , ..., P m in the forests F 1 , F 2 , ..., F m , respectively. Compressing the path P 1 in forest F 1 gets forest F 2 , compressing path P 2 into F 2 receives F 3, and so on. (And, for example, the path P k could not yet exist in the forest F and appeared only after compressing the paths P 1 , P 2 , ..., P k-1 ) It is necessary to estimate the sum of the lengths of the paths P 1 , P 2 , ... , P m (path length is the number of edges in the path). So we get an estimate for the execution time of m operations Find, because the length of the compressible path is just the number of operations “linking” the vertices in the corresponding Find.

In fact, we set out to prove an even more general statement than is necessary, because not every sequence of compression paths corresponds to the sequence of operations of Union-Find. But these nuances do not interest us.

So, there is a forest F and a sequence of squeezing paths in it in the sense that was given to it above, i.e. there is a sequence of forests F = F 1 , F 2 , ..., F m and a sequence of contractions of the paths P 1 , P 2 , ..., P m in them. Let T (m, n) denote the sum of the lengths of compressible paths P 1 , P 2 , ..., P m in the worst case, when the sum of the lengths P 1 , P 2 , ..., P m is maximal. The task is to estimate T (m, n). This is a purely combinatorial problem and all the non-trivial proofs of the effectiveness of Union-Find naturally come to one sense or another in this construction.

Evaluation of the length of the compressible path


The first essentially nontrivial step in the reasoning is the introduction of an additional parameter. The forest rank F is the maximum among the ranks of the vertices F. By T (m, n, r) we denote, similarly to T (m, n), the sum of the lengths of the compressed paths P 1 , P 2 , ..., P m in the worst case when the sum of the lengths P 1 , P 2 , ..., P m is maximal, and the initial forest has a rank not greater than r. It is clear that T (m, n) = T (m, n, n), because the rank of any forest with n vertices is less than or equal to n. The parameter r will be needed for recursive reduction of the evaluation problem for forest F to subtasks on subfields F.

Let d = log r. We divide the forest F into two non-intersecting forests F + and F - : the “upper forest” F + consists of vertices with rank> d, and the “lower forest” F - consists of all the other vertices (see figure). This split was noticed in the first proofs of estimates for Union-Find in connection with the following fact: it turns out that the upper forest F + contains significantly fewer vertices than F - .

The basic idea is to estimate roughly the lengths of the contractions of the paths lying in F + (this can be done because F + is very small), and then recursively evaluate the lengths of the contractions of the paths in F - . That is, informally, our goal is to derive the recursion T (m, n, r) ≤ T (m, n, d) + (the lengths of the paths that are not included in F - ). We begin to move towards this goal with the formalization of what F + is “very small”. Denote by | F '| the number of vertices in an arbitrary forest F '.



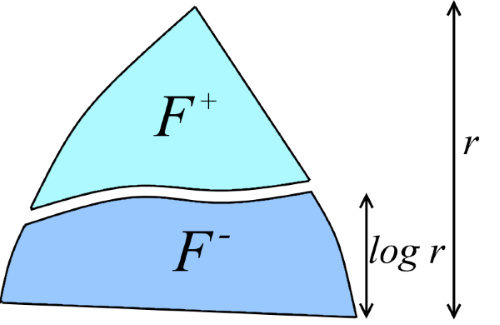
Lemma 3. Let F + be a forest consisting of vertices of F of rank> d. Then | F + | <| F | / 2 d .

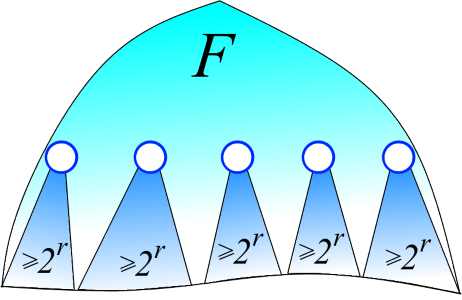
Evidence. Fix some t> d. Let us estimate how many in F + vertices of rank t. In F, by Lemma 2, the rank of a vertex is equal to the height of a tree with a root at a given vertex. Hence, a parent of a vertex with rank t necessarily has a rank> t. Thus, subtrees F with roots with rank t do not intersect (see figure below). A tree with a root of rank t by Lemma 1 contains ≥2 t vertices. Hence, there are ≤n / 2 t vertices with rank t. Running t along d + 1, d + 2, ..., we find that the number of vertices in F + is bounded above by the infinite sum n / 2 d + 1 + n / 2 d + 2 + n / 2 d + 3 + ... By the summation formula for the geometric progression we find that this sum is equal to n / 2 d . What was required.


From here on, for brevity, we will denote n + = | F + | and n - = | F - |.

The second nontrivial step in the argument. We divide the set of paths P 1 , P 2 , ..., P m into three subsets (see figure):




Each path from the P + set is divided into two paths: the upper path in F + (white vertices in the figure below to the left) and the lower path in F - (green vertices in the figure below to the left). We just shove the upper paths into the many P + paths. Denote by m + the number of paths in the set thus obtained, i.e. m + = | P + | + | P + - | (in contrast to the analogous designation | F '| for forests, | P | denotes the number of paths in the set P, and not the total number of vertices in them). Denote m - = | P - |. Then:

T (m, n, r) ≤ T (m + , n + , r) + T (m - , n - , d) + (the sum of the lengths of the lower parts of the paths from P + - ).



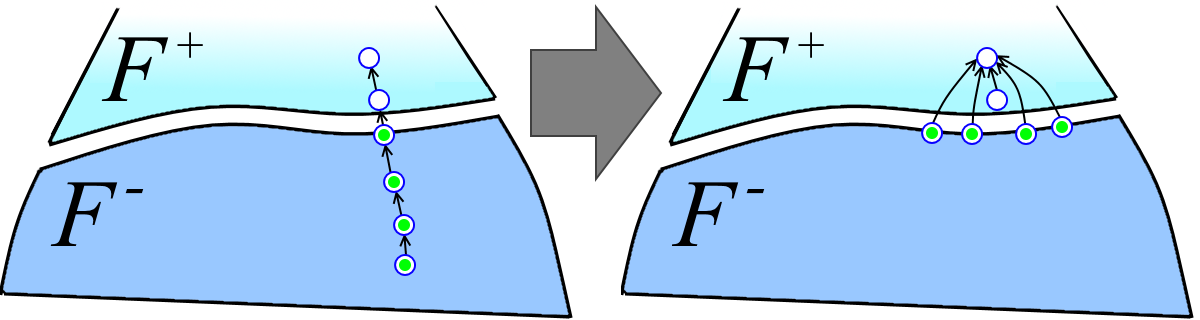
Let us estimate the sum of the lengths of the lower parts of the paths from P + - . Let P be the lower part of the path from P + - (green vertices in the figure above). All the vertices in P, except for the head, before the linking had parents from F - (the head always has a parent from F + ), and after the linking they have a parent from F + (see the figure above). Therefore, each vertex of F - can participate in some lower part of the path from P + - as a non-head one only once. It turns out that the sum of the lengths of the lower parts of the paths from the P + - is less than or equal to | P + - | + n - (one unit for each head vertex plus one unit for each vertex from F - ). Note that | P + - | ≤ m + . Therefore, the sum of the lengths of the lower parts of the paths from P + - does not exceed m + + n - .

Important note: in the reasoning done, it was unimportant that the rank F is less than or equal to d = log r; instead of log r could be any other value. If you get to this place, congratulations, we have just proved the central lemma.

The central lemma. Let F + be a forest of vertices from F with ranks> d, and F - be the forest of the remaining vertices from F. The notation m + , m - , n + , n - is defined by analogy. Then the recursion is valid: T (m, n, r) ≤ T (m + , n + , r) + T (m - , n - , d) + m + + n - .


As already mentioned, since the F + forest is very small, the length of the paths in it can be estimated by rough methods. Do this. Obviously, the compression of a path of length k in F + performs a k-1 vertex linking; that is, the k-1 vertex "rises" up the tree. The height F + does not exceed r and therefore each vertex can rise no more than r times. This means that m + path compression performs at most rn + linking (i.e., “lifting” of vertices). Hence we conclude that the sum of the lengths m + of the contractions of the paths in F + is bounded above by the number rn + + m + (one for each lift of the vertex and one for the head of each path). By Lemma 3, we obtain rn + ≤ rn / 2 d = rn / 2 log r = n. As a result, we obtain T (m + , n + , r) ≤ n + m + . Using the central lemma, we derive the recursion:

T (m, n, r) ≤ T (m + , n + , r) + T (m - , n - , log r) + m + + n - ≤
≤ n + m + + T (m - , n, log r) + m + + n =
= 2n + 2m + + T (m - , n, log r).

Now, recursively, we will continue to act in the same spirit on forest F — just as we acted on forest F, that is, just open the recursion:
T (m, n, r) ≤ (2n + 2m + ) + T (m - , n, log r) ≤
≤ (2n + 2m + ) + (2n + 2m 0 + ) + T (m 0 - , n, log log r) ≤
≤ (2n + 2m + ) + (2n + 2m 0 + ) + (2n + 2m 1 + ) + T (m 1 - , n, log log r) ≤
≤ ...
Here m 0 + , m 1 + , ... are the values ​​corresponding to m + at various levels of recursion. It is clear that m + + m 0 + + m 1 + + ... ≤ m (see the figure below). The recursion depth is the number of times you need to prologize r to get a constant. But this is log * r! As a result, we derive T (m, n, r) ≤ 2m + 2n log * r.



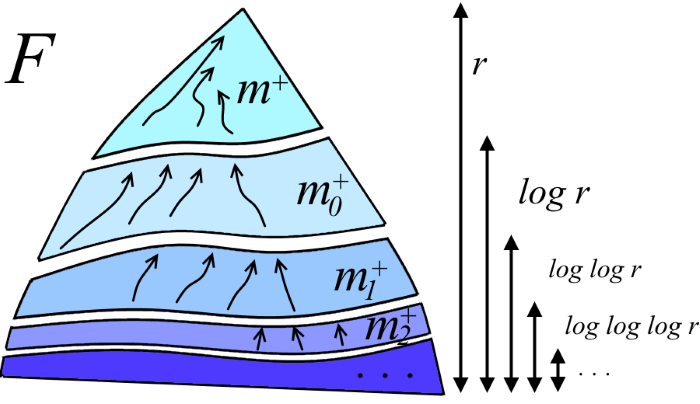
The final solution with Ackermann inverse function


If we analyze the findings more closely, we can see that, in general, the value of log r played a role only in the disclosure of the expression T (m + , n + , r) to get T (m + , n + , r) ≤ n + m + . This was achieved using Lemma 3 and naive reasoning, proving that T (m + , n + , r) ≤ rn + + m + . But in the previous section, we got a better estimate: T (m + , n + , r) ≤ 2m + + 2n + log * r. Let's redefine our main characters, “lowering” the forest F - : F + is a forest of vertices F with rank> log * r, and F - is a forest of remaining vertices with rank ≤ log * r. By analogy, we define the parameters m + , m - , n + , n - .

By Lemma 3, we obtain n + <n / 2 log * r , i.e. the F + forest is still “small” compared to F - (at first it seemed to me even counterintuitive). In the previous section, we established that T (m + , n + , r) ≤ 2m + + 2n + log * r. Hence, taking into account that 2 (n / 2 x ) x ≤ n for any integer x ≥ 1, we derive T (m + , n + , r) ≤ 2m + + 2 (n / 2 log * r ) log * r ≤ 2m + + n. This is almost like the estimate T (m + , n + , r) ≤ n + m + obtained earlier! Applying the central lemma, we obtain a recursion:

T (m, n, r) ≤ T (m + , n + , r) + T (m - , n - , log * r) + m + + n - .

Opening T (m + , n + , r) ≤ 2m + + n, we transform recursion:

T (m, n, r) ≤ T (m + , n + , r) + T (m - , n - , log * r) + m + + n - ≤
≤ 2m + + n + T (m - , n - , log * r) + m + + n - ≤
≤ 3m + + 2n + T (m - , n, log * r).

Now open a couple of levels of recursion:

T (m, n, r) ≤ (3m + + 2n) + T (m - , n, log * r) ≤
≤ (3m + + 2n) + (3m 0 + + 2n) + T (m 0 - , n, log * log * r) ≤
≤ (3m + + 2n) + (3m 0 + + 2n) + (2m 1 + + 2n) + T (m 1 - , n, log * log * log * r) ≤
≤ ...

Here, as in the last section, m 0 + , m 1 + , ... are the values ​​corresponding to m + at various recursion levels. It is clear that m + + m 0 + + m 1 + + ... ≤ m. The recursion depth is log ** r. As a result, T (m, n, r) ≤ 3m + 2n log ** r. Very good estimate. But is it possible to do this trick once more, using the estimate just obtained T (m, n, r) ≤ 3m + 2n log ** r? Yes!

I will omit the details this time. By “lowering” the forest F - to the rank of log ** r, one can again, using Lemma 3, obtain T (m + , n + , r) ≤ 3m + + n. This is almost like the estimated estimate T (m + , n + , r) ≤ 2m + + n. Then, using this estimate and the central lemma, we derive T (m, n, r) ≤ 4m + 2n log *** r.

You can continue further by “lowering” F to the rank of log *** r. In general, having done this procedure k times for any natural k, one can obtain the following estimate:
T (m, n, r) ≤ km + 2n log ** ... * r, where the number of stars is k-1.

It remains to optimize this recurrence relation. The more stars, the smaller the 2n log ** ... * r term, but the greater the km. Equilibrium is reached at some k. But we will act more rudely: we will turn the term n log ** ... * r into 2m. Before this final step, instead of r everywhere, we substitute n - the upper bound for the rank of the source forest F (although by Lemma 1, we could set r = log n, but not the essence). We introduce the following function:
α (m, n) = min {k: n log ** ... * n <2m, where the number of stars is k}.

The function α (m, n) is called the inverse function of Ackermann . Recall that we are only interested in the case of m ≥ n. By definition, α (m, n), the expression n log ** ... * n, in which α (m, n) stars, is less than 2m. Actually, we introduced the function α (m, n) to get such an effect with a minimum of stars. Maybe it was not immediately noticeable, but we just proved that m Union-Find operations are performed in O (m α (m, n)).

Tadam!



A little about the reverse function of Ackermann


If you have seen Ackermann’s inverse function before, then most likely the definition was different (more obscure), but giving asymptotically the same function as a result.The original definition of Ackermann, which Tarjan uses, personally does not tell me anything about this function (in this case, for the area for which Ackermann himself introduced his function, the definition was natural). The definition proposed by Zaydel and Sharir (and just given) reveals the “secret meaning” of Akkerman’s inverse. I also add that, strictly speaking, “the function inverse to the Ackermann function” is an incorrect name, because α (m, n) is a function of two variables and it cannot be “inverse” to any function. Therefore, it is sometimes said that α (m, n) is Akkerman's pseudoinverse . I will not give the function of Ackermann.

Now a little bit of analysis. The maximum α (m, n) is reached at m = n. Even very small deviations (for example, m ≥ n log *****n) make α (m, n) constant. The function α (n, n) grows slower than log ** ... * n for any number of stars. By the way, the definition of α (n, n) looks like the definition of iteration:

α (n, n) = min {k: log ** ... * n <2, where the number of stars is k}.

Of course, this is not the limit and there are functions that grow even slower, for example, log α (n, n). Another thing is surprising: α (m, n) arises when analyzing such a natural algorithm. Even more surprisingly, there is evidence that it is impossible to improve the resulting O (m α (m, n)) estimate.

Source: https://habr.com/ru/post/266859/

More articles:


All Articles