Walking across tiles

For motorists, the problem of unfamiliar streets was decided long ago by navigators. But even motorists walk on foot. If the store is across the road, then we get up and go. Difficulties arise if you have to walk five hundred meters along an unfamiliar street and turn off two or three times.

None of the services we know built a route from point A to point B where there are no paths and sidewalks, but it’s full of fences and houses of fancy shapes.
')
2GIS solved this problem. We learned to build routes for pedestrians on rasterized map of the area. A map is formally represented as a graph with vertices on a regular grid in places where a pedestrian may be physically located.

It is considered that such a way to build routes is unacceptable, because it eats up a lot of resources. Under the cut - how we coped with it.

Algorithm

We depict the algorithm for constructing a walking route.

1. Rasterize the terrain with a resolution of 2 × 2 meters. Homes, roads, fences, reservoirs, passages, ravines get under rasterization ... In the simplest case, each pixel is assigned a value - it is possible or impossible to pass. But nothing prevents graduate patency:
   
   • can pass quickly
   • you can go
   • pass with difficulty
   • don't pass
   Priority is important. We put obstacles on the initially traversed area: houses, impassable roads, fences, ravines, railways ... Then we cut passable roads and pedestrian crossings with railway crossings in the form of circles with a diameter slightly wider than the road.
2. We consider a terrain map as a description of a graph with implicitly indicated relationships between adjacent cells. Going only in passable, in which we have not yet been.
3. We work with the graph. If we are looking for a passage from point to point, we use a variant of algorithm A * .
   If we are looking for the nearest road, determining the passage to the nearest of the registered objects, then we start the search wave with an honest Dijkstra algorithm .
   

Two things scare in this scheme: memory and memory. Online and on disk. Both that and that are spent too quickly. Let's try to solve the problem.

Fighting for RAM

Each point has potentially 8 pairs of edges - direct and reverse. Per square kilometer it turns out: 500 × 500 × 8 = 2 000 000. If you act head-on, you will have to process and save each ...

To save RAM, we divide the map into tiles of 256 × 256 cells or 512 × 512 meters. We will only store the perimeter of the wave that passes along the borders of the tiles. For the storage of the perimeter, we will create a common “ heap ”.

Tiles are processed atomically. When pouring a tile, use its local heap. The algorithm is as follows:

1. Find the tile at which the starting point falls, and add the point to the local “heap” of this tile.
2. We let the wave in the tile. If, when pouring, we have reached the finish line, then go to step 7. If not, then when the wave floods the entire tile, we will get the lengths from the starting point on its borders.
3. We bring this perimeter into the common heap. The tile itself is no longer needed, it can be released.
4. We take the minimum element from the general “heap”, look at which tile and on which side this element is looking.
5. We remove all points from this side of this tile from the common heap and memorize them.
6. Load a new tile. In his local heap from the right side we put the found points. Returning to point 2 again.
7. After the path is found (this is actually a list of points on the inter-tile grid), we restore the real path inside the tiles. We do this because we have unloaded the tiles ourselves a long time ago to save memory. To do this, we go down our path, load tiles one by one, and rebuild the route, but this time from point to point inside the tile.
8. Found the way straighten to get rid of the characteristic "saw". The method, though not eliminating all the artifacts, but quickly eliminates the most obvious.
   For this inside the tile we use the Brezenham algorithm . To straighten the pieces of the path, we draw a line between the pieces and follow the mask of obstacles to see if this line is passable.
   Between the tiles, we also straighten the path. To do this, take the penultimate point of the previous tile and the second current one. We find on the lattice a point that sweeps the line intersecting them. In both tiles, Bresenham is trying to go directly to this border point. If possible - voila! - we connect directly.

Let's see the distribution of the cost inside the tile:



Color - from blue to orange - indicates the length
traveled path. We left the upper right corner.


Thus, we manage to limit ourselves to a minimum of memory for storing the wave perimeter. Even tiles are not required to be cached. We consider this option acceptable, and the goal of saving RAM is achieved.

Fighting for disk storage

To store one tile of 256 × 256 pixels with a resolution of 1 bit per pixel, 8 kilobytes is required. Then a square kilometer costs 32 kilobytes, and a typical city with surroundings - 100 × 100 km already weighs 320 MB.

Too much. But this kind of information should be well compressed, since it contains significant distortions in the ratio of 0 and 1. In addition, there are long monotonic sequences.

Initially, taking this into account, we applied an adaptive arithmetic encoder. The rasterization of Novosibirsk took about four minutes. It turned out 4946 non-empty tiles, which took about 10 MB. At the same time, the same data in gifs occupies only 6 MB (which is humiliating :-). It looks like this:



Several random tiles in the form of pictures


10 or even 6 MB for Novosibirsk is more than our routing index occupies.

In addition, if we walk not from point to point, but to the road, then we need another raster — with roads that a pedestrian can reach. This is too much. We found another solution - rasterization "on the fly."

Rasterization on the fly

At first glance, this approach does not require additional information. In fact, we already have the information: houses, fences, roads — with just a dozen layers.

But then for rasterization of each tile, you will have to do 10 spatial queries to spatial indices, followed by subtraction from the corresponding spatial layers.

With mobile phone restrictions on available memory, the data warehouse has almost no cache. And the “alien” subsystem - we do not have a trusting relationship with it, so the memory is allocated through CRT, which is not very good in terms of fragmentation.

Simply put, this option is too expensive. So we made our data warehouse for rasterization.

For storage of geometries, a B-tree is used with a key of 3 elements (or of two + value, you wish):

1. TileID is a tile identifier. The extent of the map is broken into tiles, numbering goes line by line from bottom to top, from left to right.
2. Attr - an attribute of the object. Use only 1 low bit. 0 - the object is rasterized by ones, 1 - by zeros.
   When the tree is traversed, the zeros go forward, and we first draw all the blocking objects (houses, fences), and then overlay the resolving objects (wickets, crossings).
3. Shp - geometry, all types of geometries are packed together.

Such an organization for one search and one traverse finds the data of this tile. It uses mainly stack objects. Additional memory is taken from the pool, which is noticeably more humane in relation to CRT.

Geometries at the export stage are clipped along the borders of the tiles. When writing a tree data is compressed. As a result, storage of vector information is three times smaller than rasterized, when compared with an adaptive arithmetic coder, and twice as efficient as gif.

Route examples

We go from point to point, we go through the train. relocation




Again from point to point. Sometimes the path of a pedestrian in the urban jungle can be complicated.




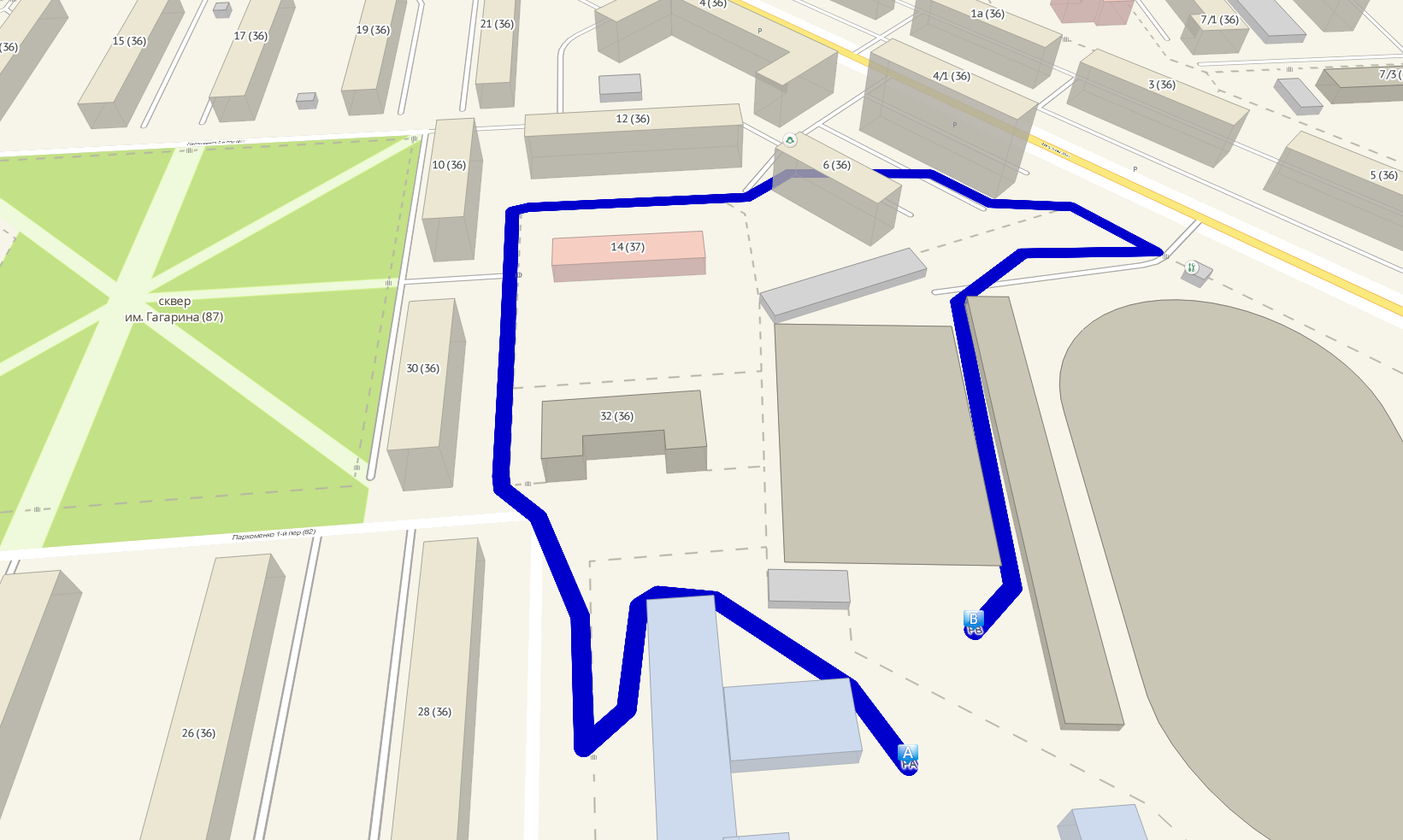
We go to the nearest road.




Again to the nearest rib.

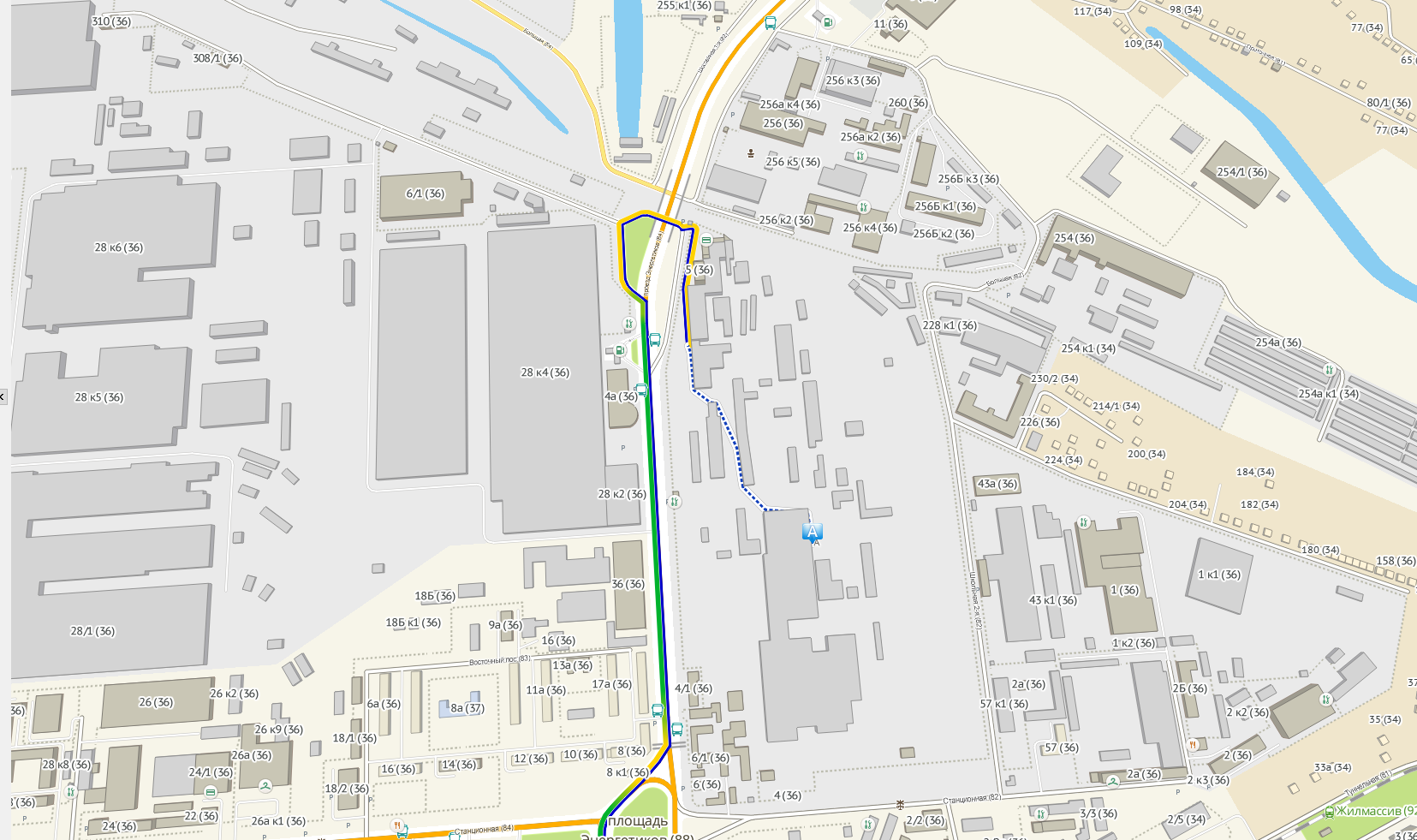
What is the result

The amount of additional data for Novosibirsk is about 3 MB. The capital of our vast country is 8Mb. Search for 1.5 km on the desktop takes 90 ms without warming up. These are about 20 unpacked and processed tiles. Additional RAM is usually required less than a megabyte.

But the approach has flaws. Despite the "straightening" of geometries, sometimes the result is rather strange. For example, due to the discreteness of the rasterization, buildings “stick together” from time to time.

The algorithm is quadratic to distance and nothing can be done about it. Fortunately, it is extremely rare to build at such distances when it becomes a problem. In fact, we limit the pedestrian passage to two kilometers.

And yet, it is better than attracting directly to the nearest roads and walking through the cities and villages, despite the obstacles. Walking routes are already working in mobile applications on iOS and Windows Phone, and when searching for directions to public transport on 2gis.ru.