Accelerate vectorization and memory accesses in DL_MESO: optimization examples with Vectorization Advisor on a large project
We have already written about Vectorization Advisor and examples of its use in simple samples . Today we will share information about how Intel engineers, together with researchers from STFC Daresbury Laboratory in the UK, optimized the DL_MESO package.

DL_MESO is a scientific package for simulating condensed media at the mesoscopic level (forgive me, chemists and physicists, if not correctly translated). The package was developed in the Daresbury laboratory and is widely used both in the research community and in the industry (by Unilever, Syngenta, Infineum). With this software, optimal formulas for shampoos, fertilizers and fuel additives are sought. This process is called “Computer Aided Formulation” (CAF) - I translated it as “CAD in the field of developing chemical formulas”.
')
CAF simulation is a very resource-intensive computation, so developers were immediately interested in the most productive design. And DL_MESO was chosen as one of the joint projects in the “Intel Parallel Computing Center” (IPCC) between Intel and Hartree.
The developers of DL_MESO wanted to take advantage of the hardware capabilities of vector parallelism, because future technologies like AVX-512 can potentially make code 8 times faster on double-precision numbers (compared to non-vectorized code).
In this post we will describe how scientists from Darsbury used Vectorization Advisor to analyze Lattice Boltzmann Equation code in DL_MESO, what specific problems they found, and how to fix their code to overclock it 2.5 times.
What is the Vectorization Advisor, read the first article . Here we go straight to the Surt profile of the Lattice Boltzman component. About half of the total execution time falls on ten “hot” cycles, among which there are no obvious leaders, each spending no more than 12% of the total program time. This picture is close to the “flat profile” (flat profile), which is usually bad for a programmer. After all, to achieve significant acceleration, it is necessary to optimize each of the cycles separately.
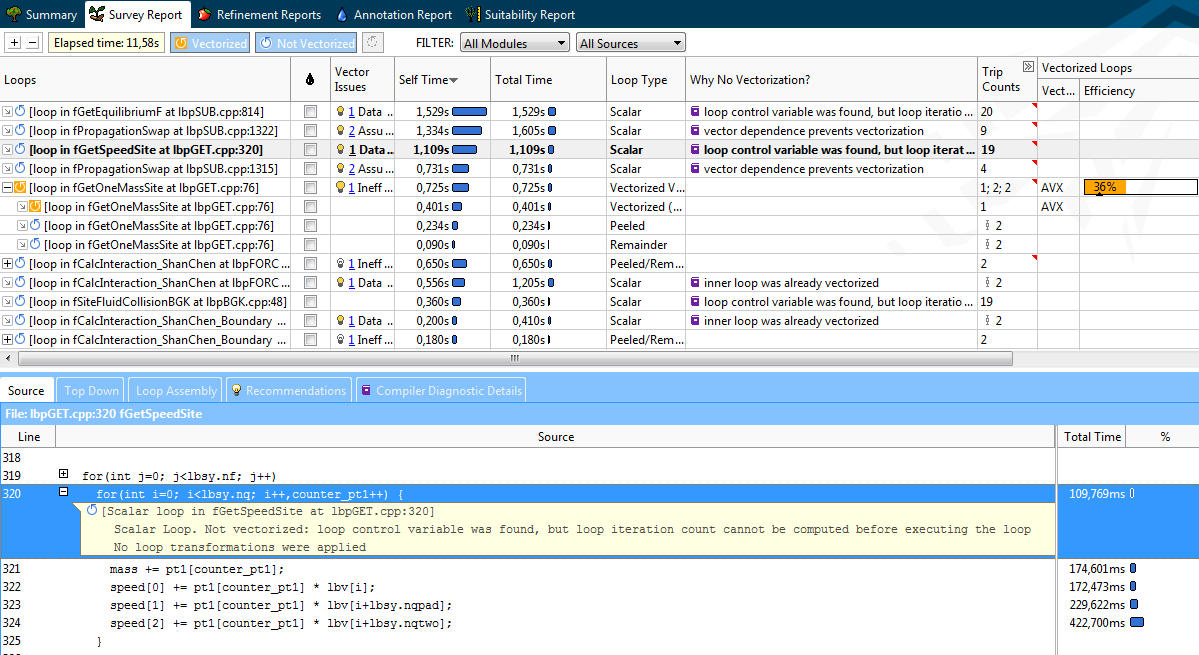
But, fortunately for developers from Darsbury, Vectorization Advisor can quickly characterize the cycles as follows:
Vectorization Advisor not only provides information on cycles. The Recommendations and Compiler Diagnostic Details tabs let you know about specific problems and how to solve them.
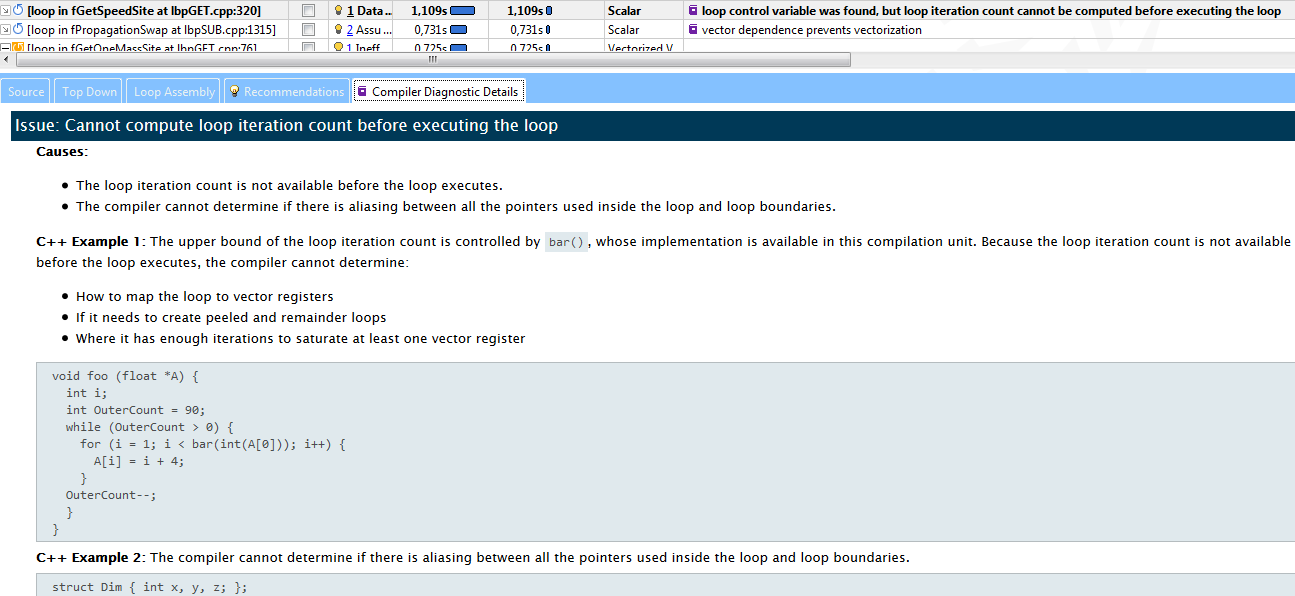
In our case, the third hotspot (“hot” cycle, forgive me the guardians of the purity of the language) in fGetSpeedSite could not vectorize because the compiler could not estimate how many iterations it would have. Compiler Diagnostic Details describes the essence of the problem with an example and suggestions for solving it - add the "#pragma loop count" directive. Following the advice, this cycle was quickly vectorized and moved from category 2 to category 4.
Even when the code can be vectorized, this does not necessarily immediately lead to an increase in productivity (categories 2 and 3). Therefore, it is important to investigate already vectorized cycles for their effectiveness.
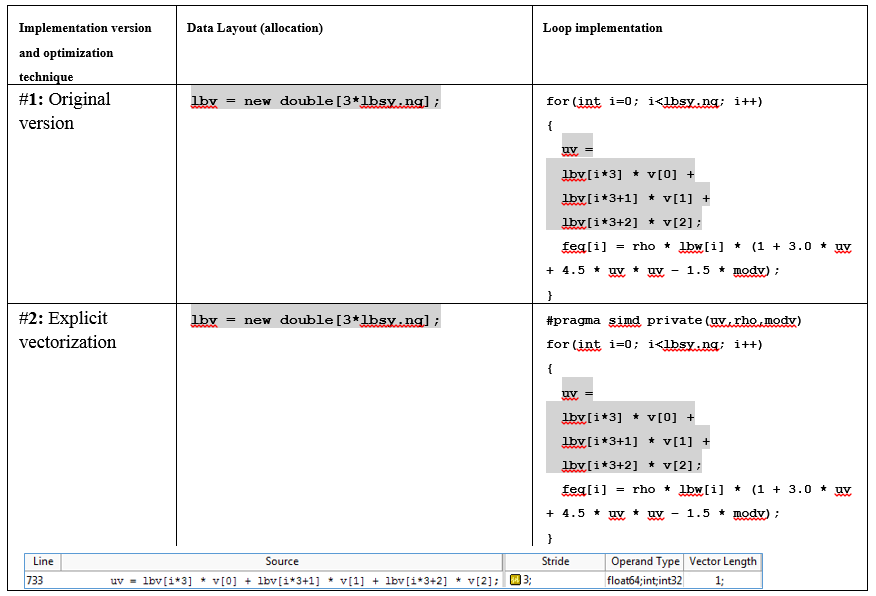
The lbv array stores speeds for the spatial grid in all dimensions. The variable lbsy.nq contains the number of speeds. The model represents a three-dimensional 19-speed grid (scheme D3Q19). Those. The value lbsy.nq is 19. The resulting equilibrium is stored in the array feq [i].
In the first analysis, the cycle was scalar, not vectorized. By simply adding "#pragma omp simd" before the loop, it was vectorized, and its share in total CPU time dropped from 13% to 9%. But even with these changes, there is still room for improvement.
New result Advisor XE showed that the compiler generated not one, but two cycles:
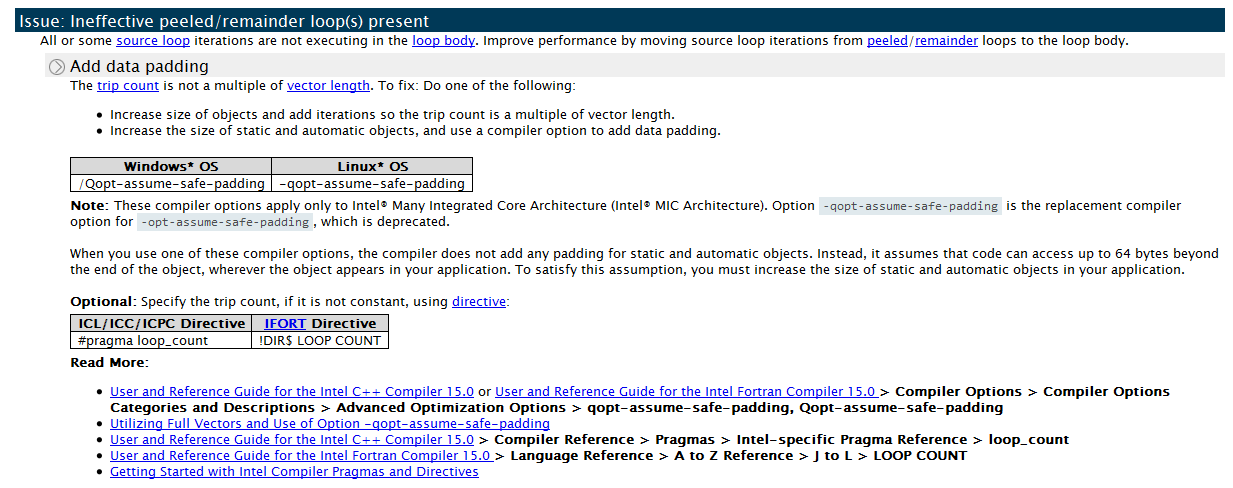
This Scalar remainder is an unnecessary overhead. Its presence is detrimental to parallel efficiency. Such a large "weight" remainder is caused by the fact that the number of iterations is not divisible by VL (vector length) exactly. The compiler generates vector instructions for iterations 0-15, and the remaining iterations from 16 to 18 are executed in the scalar remainder. 3 iterations, and even slowly running consistently, and make up 30% of the cycle time. Ideally, all iterations should be executed in a vector code, and there should be no remainder at all.
We can apply the data padding technique to our cycle. Increase the number of iterations to 20, which will be a multiple of VL (4). Advisor XE explicitly advises doing this in the Recommendations tab:
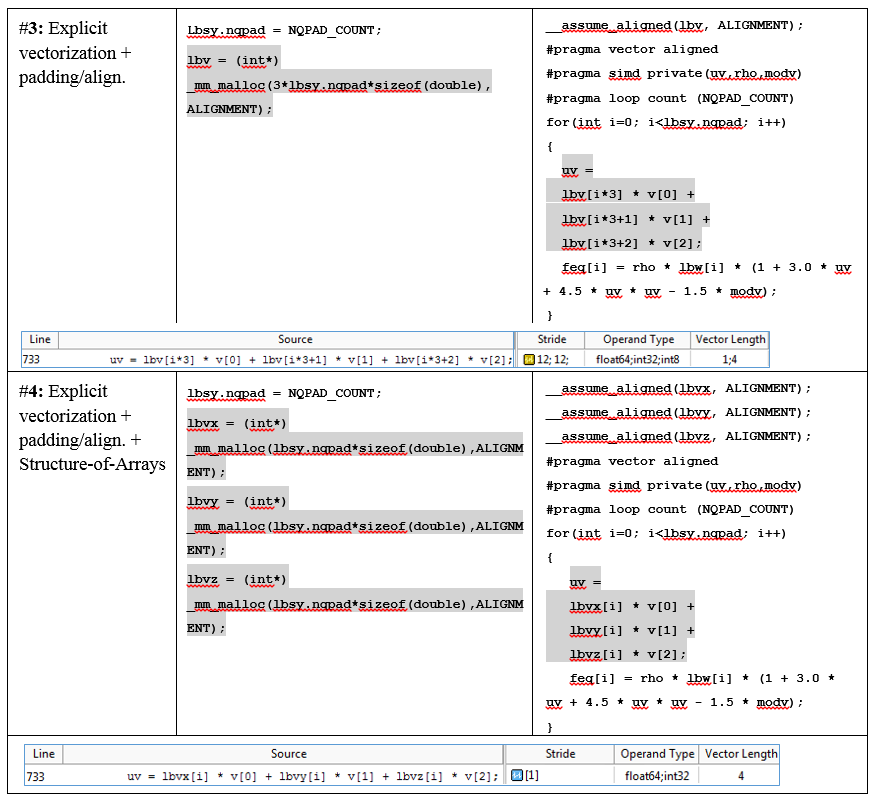
To tamper with the data, you will need to increase the size of the feq [], lbv [], and lbw [] arrays in order not to get a segmentation fault. The table at the end of the article shows the changes in the code. The value of lbsy.nqpad is the sum of the original number of iterations and the value of padding (NQPAD_COUNT).
In addition, the DL_MESO developers added a “#pragma loop count” directive before the loop. Clearly seeing that the number of iterations is a multiple of VL, the compiler generates a vector code, and the remainder is not executed.
In the DL_MESO code there are many of the same constructions that can be improved in the same way. We fixed three other cycles in the same source file and received 15% acceleration of each of them.
The tamping technique used for the first two cycles has its price:
In our case, the positive effect on performance outweighed the cons, and the code complication was acceptable.
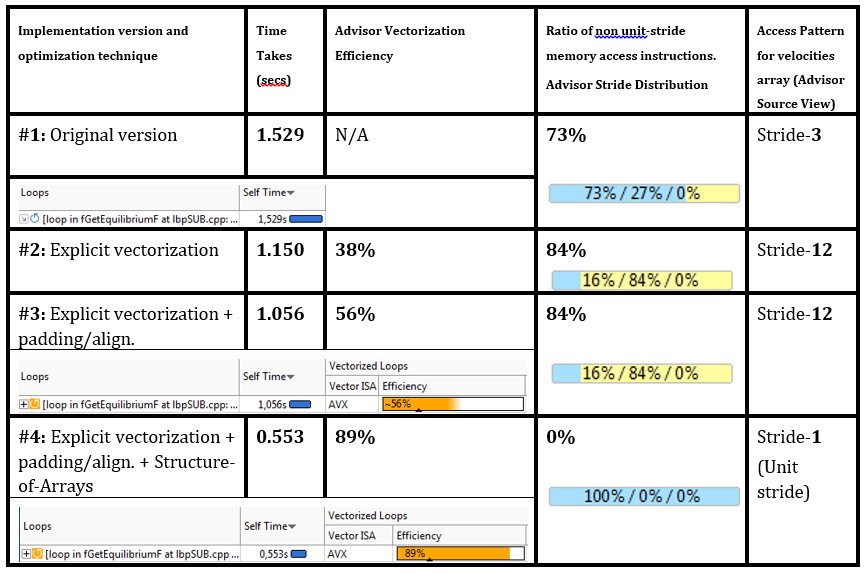
Vectorization, data padding and data alignment improved the performance of No. 1 hotspot by 25–30%, the vectorization efficiency according to Advisor XE increased to 56%.
Since 56% is still far from 100%, the developers decided to investigate what blocks productivity growth. Looking again at “Vector Issues / Recommendation”, they discovered a new problem - “Possible inefficient memory access patterns present”. The recommendation is to run the “Memory Access Pattern” (MAP) analysis. The same advice was in the Traits column:

To start the MAP analysis, the developer marks the desired cycles and presses the MAP start button on the Workflow panel.

The distribution of strides as a result of the MAP shows the presence of a unit-stride (sequential access) and non-unit “constant” stride - memory accesses with a constant step:

The MAP data in the source code indicates that there are references to strayd 3 (for the original scalar version) and strajd 12 (for the vectorized version with padding) when accessing the lbv array (see table at the end).
The call in step 3 occurs to the elements of the velocity array lbv. Each new iteration is shifted by 3 elements of the array. Where 3 comes from is clear from the expression lbv [i * 3 + X], to which our memory references are attributed.
Such inconsistent access is not very good for vectorization, because it does not allow to load all the elements into the vector register for one instruction of the type mov (its “packed” version is called differently). But treatment with a constant step can often be converted to sequential access by applying a transformation from an “array of structures” to a “structure of arrays”. Note that after the MAP analysis, the recommendations window advises exactly this (AoS-> SoA) to solve the problem of inefficient memory access - see the screenshot above.
The developers applied this conversion to the lbv array. To do this, the lbv array, initially containing the speeds for X, Y, and Z, was divided into three arrays: lbvx, lbvy, and lbvz.
The developers of DL_MESO say that the transformation of the structure of arrays was laborious compared to padding, but the result justified the efforts - the cycle in fGetEquilibrium became 2 times faster, and similar improvements happened with several more cycles working with the lbv array.
The results of data structure transformation and loop optimization (padding, leveling), along with performance metrics and memory access patterns Advisor XE:
The evolution of the source code of the considered cycle - vectorization directives, alignment, padding, AoS -> SoA transformation, along with the results of the MAP from Advisor XE:
Using the DL_MESO analysis in Vectorization Advisor and adding a few directives to the code, we managed to reduce the time of the three hottest cycles by 10-19%. All optimizations were based on Advisor recommendations. Work was done on “turning on” vectorization and improving loop performance using “data padding” (padding). By applying similar techniques to several more cycles, the acceleration of the entire application by 18% was obtained.
The following major improvement was obtained when data was transformed: the “array of structures” into the “structure of arrays”. Again, based on the recommendation of Advisor XE.
In addition, the work and tests were originally conducted on servers with Xeon processors (Advisor does not work on the coprocessor). When the same thing was done for the code running on the Xeon Phi coprocessor, about the same gain was obtained - the coprocessor was optimized without additional efforts.
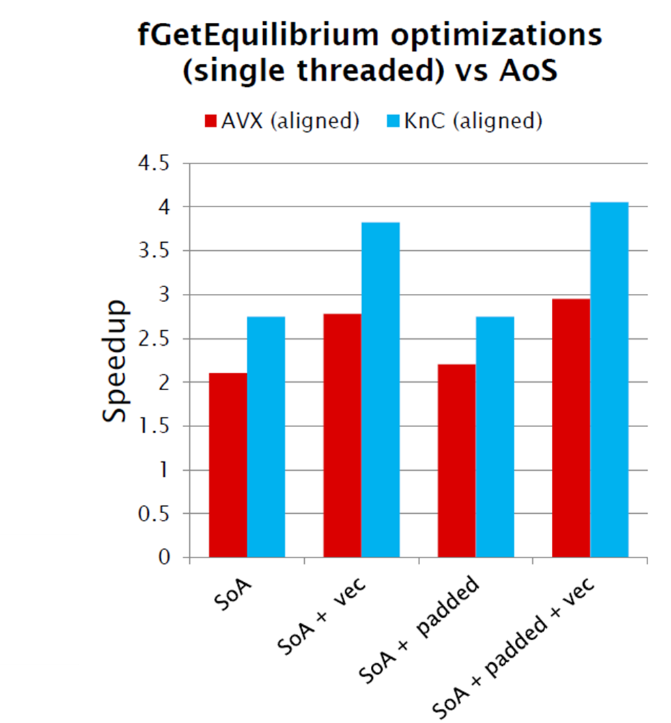
Below is the acceleration obtained on a regular server (labeled AVX) and on a Xeon Phi map (labeled KnC). On the Xeon CPU they accelerated 2.5 times, on the Xeon Phi - 4.1 times:
This is a quote from the DL_MESO developer: “Luke Mason, computational scientists in Daresbury lab).
This post is a translation of an article by Zakhara Matveyev (Intel Corporation).

DL_MESO is a scientific package for simulating condensed media at the mesoscopic level (forgive me, chemists and physicists, if not correctly translated). The package was developed in the Daresbury laboratory and is widely used both in the research community and in the industry (by Unilever, Syngenta, Infineum). With this software, optimal formulas for shampoos, fertilizers and fuel additives are sought. This process is called “Computer Aided Formulation” (CAF) - I translated it as “CAD in the field of developing chemical formulas”.
')
CAF simulation is a very resource-intensive computation, so developers were immediately interested in the most productive design. And DL_MESO was chosen as one of the joint projects in the “Intel Parallel Computing Center” (IPCC) between Intel and Hartree.
The developers of DL_MESO wanted to take advantage of the hardware capabilities of vector parallelism, because future technologies like AVX-512 can potentially make code 8 times faster on double-precision numbers (compared to non-vectorized code).
In this post we will describe how scientists from Darsbury used Vectorization Advisor to analyze Lattice Boltzmann Equation code in DL_MESO, what specific problems they found, and how to fix their code to overclock it 2.5 times.
Survey Profile
What is the Vectorization Advisor, read the first article . Here we go straight to the Surt profile of the Lattice Boltzman component. About half of the total execution time falls on ten “hot” cycles, among which there are no obvious leaders, each spending no more than 12% of the total program time. This picture is close to the “flat profile” (flat profile), which is usually bad for a programmer. After all, to achieve significant acceleration, it is necessary to optimize each of the cycles separately.

But, fortunately for developers from Darsbury, Vectorization Advisor can quickly characterize the cycles as follows:
- Vectorized but not vectorized cycles that require minimal code changes (usually using OpenMP4.x) to enable the generation of a SIMD code. The first 4 cycles (CPU time) fall into this category.
- Vectorized cycles, the performance of which can be improved by simple manipulations.
- Vectorized loops whose performance is limited by the data layout structure. Optimization of such cycles requires more serious processing of the code. As we will see later, after eliminating problems with the first two categories, the two most loaded cycles will become such.
- Vectorized cycles that already work well.
- All other cases (including non-vectorized cycles).
Vectorization Advisor not only provides information on cycles. The Recommendations and Compiler Diagnostic Details tabs let you know about specific problems and how to solve them.
In our case, the third hotspot (“hot” cycle, forgive me the guardians of the purity of the language) in fGetSpeedSite could not vectorize because the compiler could not estimate how many iterations it would have. Compiler Diagnostic Details describes the essence of the problem with an example and suggestions for solving it - add the "#pragma loop count" directive. Following the advice, this cycle was quickly vectorized and moved from category 2 to category 4.

Even when the code can be vectorized, this does not necessarily immediately lead to an increase in productivity (categories 2 and 3). Therefore, it is important to investigate already vectorized cycles for their effectiveness.
Simple optimization: padding in the equilibrium distribution core
int fGetEquilibriumF(double *feq, double *v, double rho) { double modv = v[0]*v[0] + v[1]*v[1] + v[2]*v[2]; double uv; for(int i=0; i<lbsy.nq; i++) { uv = lbv[i*3] * v[0] + lbv[i*3+1] * v[1] + lbv[i*3+2] * v[2]; feq[i] = rho * lbw[i] * (1 + 3.0 * uv + 4.5 * uv * uv - 1.5 * modv); } return 0; } The lbv array stores speeds for the spatial grid in all dimensions. The variable lbsy.nq contains the number of speeds. The model represents a three-dimensional 19-speed grid (scheme D3Q19). Those. The value lbsy.nq is 19. The resulting equilibrium is stored in the array feq [i].
In the first analysis, the cycle was scalar, not vectorized. By simply adding "#pragma omp simd" before the loop, it was vectorized, and its share in total CPU time dropped from 13% to 9%. But even with these changes, there is still room for improvement.
New result Advisor XE showed that the compiler generated not one, but two cycles:
- Vectorized loop body with a long vector (Vector Length - VL) equal to 4 - 4 doubles in the 256-bit AVX register.
- Scalar remainder, consuming 30% of the time of this cycle.
This Scalar remainder is an unnecessary overhead. Its presence is detrimental to parallel efficiency. Such a large "weight" remainder is caused by the fact that the number of iterations is not divisible by VL (vector length) exactly. The compiler generates vector instructions for iterations 0-15, and the remaining iterations from 16 to 18 are executed in the scalar remainder. 3 iterations, and even slowly running consistently, and make up 30% of the cycle time. Ideally, all iterations should be executed in a vector code, and there should be no remainder at all.
We can apply the data padding technique to our cycle. Increase the number of iterations to 20, which will be a multiple of VL (4). Advisor XE explicitly advises doing this in the Recommendations tab:

To tamper with the data, you will need to increase the size of the feq [], lbv [], and lbw [] arrays in order not to get a segmentation fault. The table at the end of the article shows the changes in the code. The value of lbsy.nqpad is the sum of the original number of iterations and the value of padding (NQPAD_COUNT).
In addition, the DL_MESO developers added a “#pragma loop count” directive before the loop. Clearly seeing that the number of iterations is a multiple of VL, the compiler generates a vector code, and the remainder is not executed.
In the DL_MESO code there are many of the same constructions that can be improved in the same way. We fixed three other cycles in the same source file and received 15% acceleration of each of them.
Overhead balancing and optimization tradeoffs
The tamping technique used for the first two cycles has its price:
- In terms of performance, we eliminate the overhead in the scalar remainder, but introduce additional calculations in the vector part.
- From the point of view of supporting the code, we redid the allocation of data structures and potentially included values in the compiler directives, depending on the size of the input data and the type of load.
In our case, the positive effect on performance outweighed the cons, and the code complication was acceptable.
Optimizing data layout: array structures
Vectorization, data padding and data alignment improved the performance of No. 1 hotspot by 25–30%, the vectorization efficiency according to Advisor XE increased to 56%.
Since 56% is still far from 100%, the developers decided to investigate what blocks productivity growth. Looking again at “Vector Issues / Recommendation”, they discovered a new problem - “Possible inefficient memory access patterns present”. The recommendation is to run the “Memory Access Pattern” (MAP) analysis. The same advice was in the Traits column:

To start the MAP analysis, the developer marks the desired cycles and presses the MAP start button on the Workflow panel.

The distribution of strides as a result of the MAP shows the presence of a unit-stride (sequential access) and non-unit “constant” stride - memory accesses with a constant step:

The MAP data in the source code indicates that there are references to strayd 3 (for the original scalar version) and strajd 12 (for the vectorized version with padding) when accessing the lbv array (see table at the end).
The call in step 3 occurs to the elements of the velocity array lbv. Each new iteration is shifted by 3 elements of the array. Where 3 comes from is clear from the expression lbv [i * 3 + X], to which our memory references are attributed.
Such inconsistent access is not very good for vectorization, because it does not allow to load all the elements into the vector register for one instruction of the type mov (its “packed” version is called differently). But treatment with a constant step can often be converted to sequential access by applying a transformation from an “array of structures” to a “structure of arrays”. Note that after the MAP analysis, the recommendations window advises exactly this (AoS-> SoA) to solve the problem of inefficient memory access - see the screenshot above.
The developers applied this conversion to the lbv array. To do this, the lbv array, initially containing the speeds for X, Y, and Z, was divided into three arrays: lbvx, lbvy, and lbvz.
The developers of DL_MESO say that the transformation of the structure of arrays was laborious compared to padding, but the result justified the efforts - the cycle in fGetEquilibrium became 2 times faster, and similar improvements happened with several more cycles working with the lbv array.
The results of data structure transformation and loop optimization (padding, leveling), along with performance metrics and memory access patterns Advisor XE:

The evolution of the source code of the considered cycle - vectorization directives, alignment, padding, AoS -> SoA transformation, along with the results of the MAP from Advisor XE:


Summary
Using the DL_MESO analysis in Vectorization Advisor and adding a few directives to the code, we managed to reduce the time of the three hottest cycles by 10-19%. All optimizations were based on Advisor recommendations. Work was done on “turning on” vectorization and improving loop performance using “data padding” (padding). By applying similar techniques to several more cycles, the acceleration of the entire application by 18% was obtained.
The following major improvement was obtained when data was transformed: the “array of structures” into the “structure of arrays”. Again, based on the recommendation of Advisor XE.
In addition, the work and tests were originally conducted on servers with Xeon processors (Advisor does not work on the coprocessor). When the same thing was done for the code running on the Xeon Phi coprocessor, about the same gain was obtained - the coprocessor was optimized without additional efforts.
Below is the acceleration obtained on a regular server (labeled AVX) and on a Xeon Phi map (labeled KnC). On the Xeon CPU they accelerated 2.5 times, on the Xeon Phi - 4.1 times:

This is a quote from the DL_MESO developer: “Luke Mason, computational scientists in Daresbury lab).
This post is a translation of an article by Zakhara Matveyev (Intel Corporation).
Source: https://habr.com/ru/post/266685/
All Articles