Good day! We recently started a series of articles on collaborative editing. In the first article I talked about the task of non-blocking editing and possible approaches to its implementation. I recall that in the end we chose Operation Transformation (OT) as the algorithm. A story about its client-server version was also announced, and today I will cover the details of his work. In addition, you will find out why the cancellation in OT works differently and how it faces a collision with harsh reality.

Next you will find a lot of algorithms and diagrams. I think you will be interested.

Client-server model

At the end of the previous article I noted that the difficulties in implementing the OT approach can be circumvented at the expense of the central server. Unlike the peer-to-peer algorithm, using a server allows you to enter a general order of operations — the order of operations on the server. Accordingly, at any moment in time the status of the document on the server is characterized by one number - revision.
')


In this case, the status of the document at any of the clients at any time can be represented as a certain revision on the server and a certain number of local operations that are still not coordinated with the server.

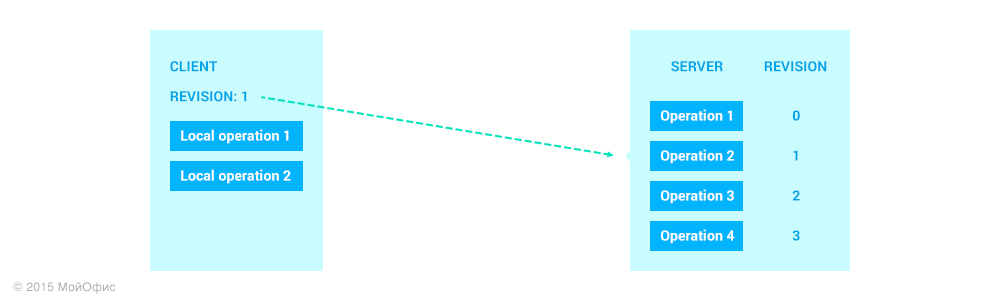
From server to client

To begin with, let's look at what happens when a new operation comes from the server to the client. In this situation, everything is quite clear. It is assumed that all operations come to us in the order in which they are applied on the server. For this reason, the audit of the operation is known to us (audit on the client + 1).



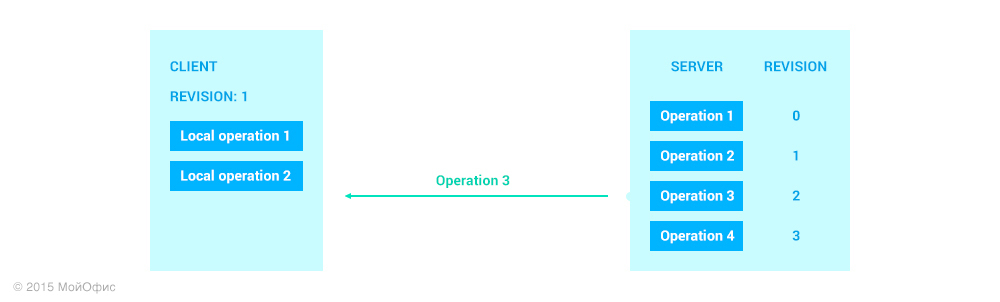
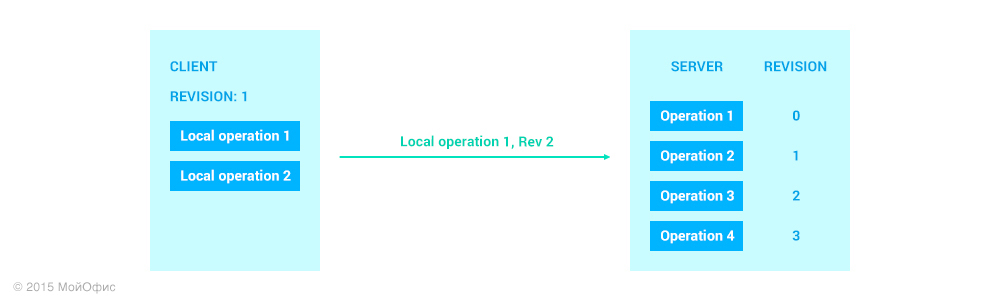
Revision 1 is the most recent overall document state for the server and this client. Recall the transformations that we covered in the previous article. With their help, we can "reduce" various ways of document modifications:



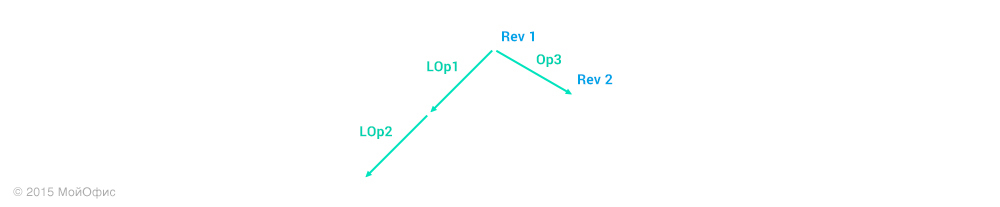
For clarity, in this and the following diagrams I will use abbreviations, where Operation3 is Op3, Local operation 1 is LOp1, and so on. The right shoulder is the actions that are performed on the server. And the left - on the client. We use the transformation property described in the diagram in the last article:



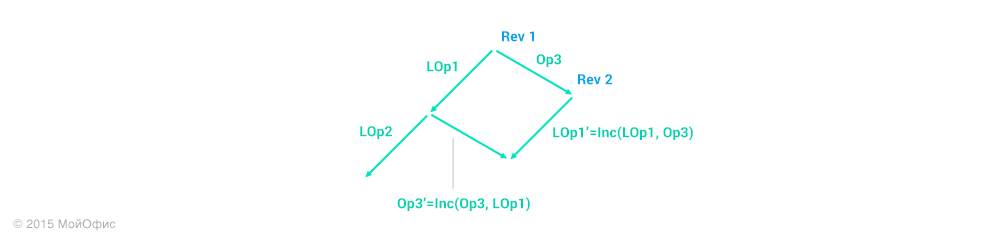
Repeat this action again:



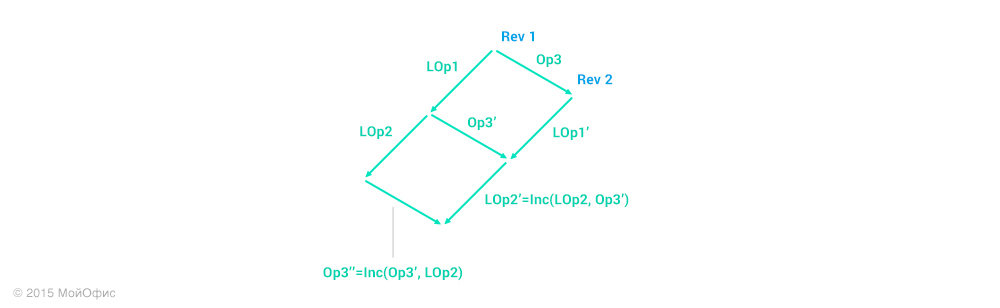
Then we can act in two directions:

1. Apply the operation Op3 '' on the client, increment the revision and replace the local operations (LOp1, LOp2) with (LOp1 ', LOp2' ').
2. Roll back local operations and consistently apply Op3, LOp1 ', LOp2' '.

Whichever option we choose, the result is the client’s state:



Based on all the considerations given at the moment, everything looks like that the results in both variants will be similar. And the first one is preferable for performance reasons. But we use exactly the second method. I will tell you why this is due in one of the following articles. In the meantime, take it as it is and continue.

From client to server

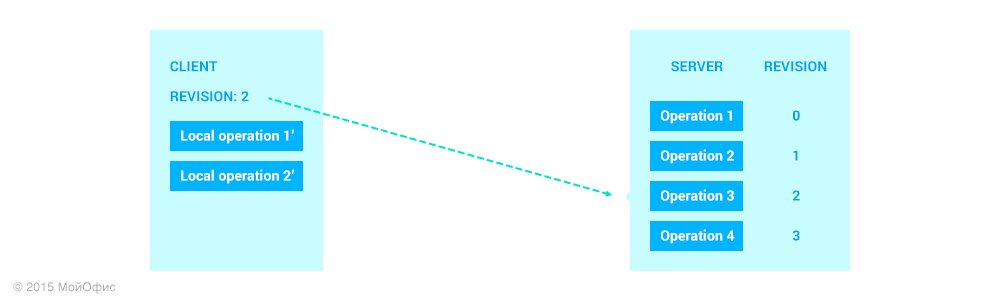
After we have disassembled sending data from the server towards the client, consider the operations in the opposite direction. Let's return to the same state as in the example above:



As you can see, along with the operation itself, the client sends a revision that is common to the client and the server at the moment. This eliminates the need for the server to restore the revision on which the sent operation was based. Reapply the transformation:



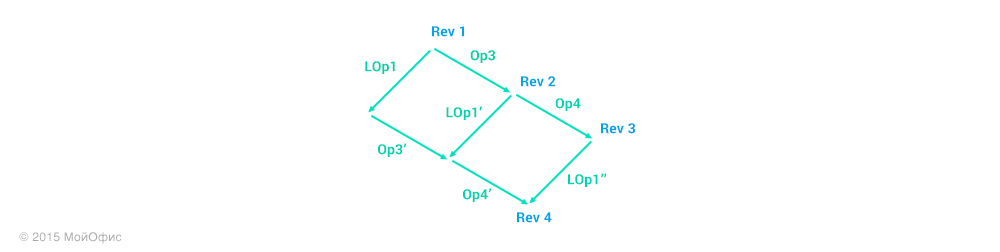
Here we can see that on the server it is necessary to apply the operation LOp1 ′ ′ and, accordingly, to increase the audit. In addition, the transformed operation, we must send to the rest of the clients who work with the document:



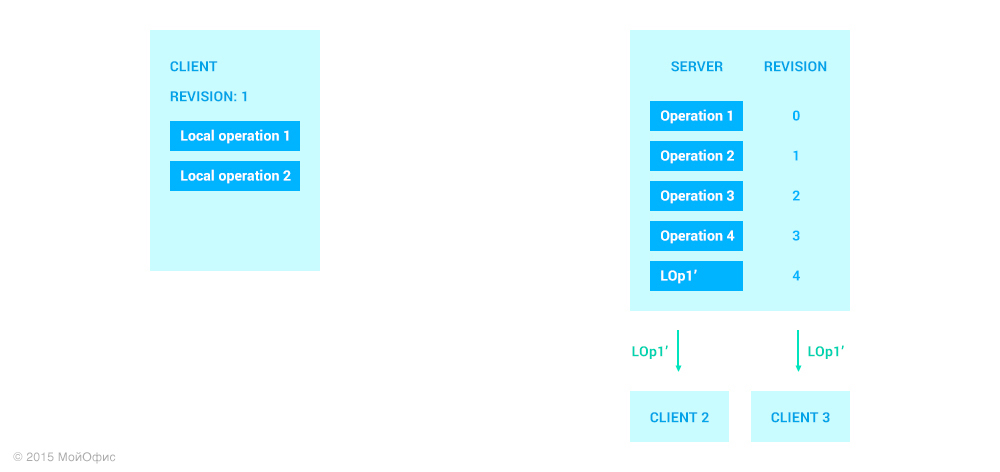
Please note that the client status has not changed. In order for him to be able to increase the audit, the server needs to send him a confirmation. This implies that the communication channel keeps the order of message delivery, which means that all operations with a revision smaller than that of LOp1 ′ will be sent to the client beforehand.

In this case, the procedure for the client to receive operations from the server ensures that after all transformations the first of the local operations will have the value LOp1 ′, the same as the corresponding operation on the server.



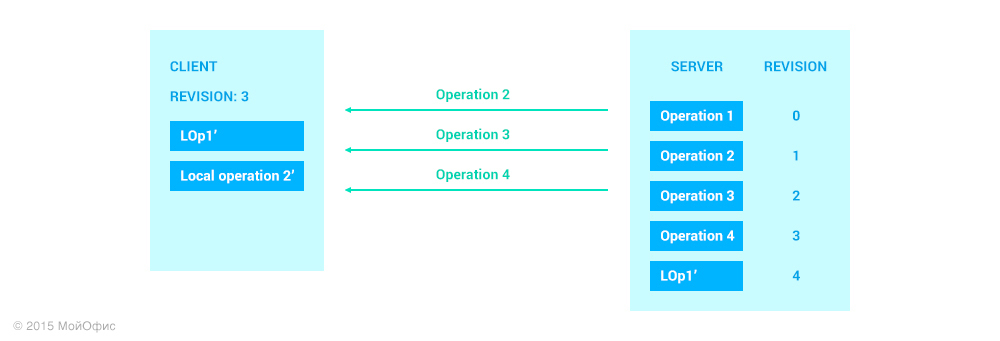
After receiving a confirmation message, the client increases the value of the revision. The value of this revision will be equal to the revision on the server that corresponds to the sent operation. We also remove LOp1 ′ from the list of local client operations, as it is now on the server.

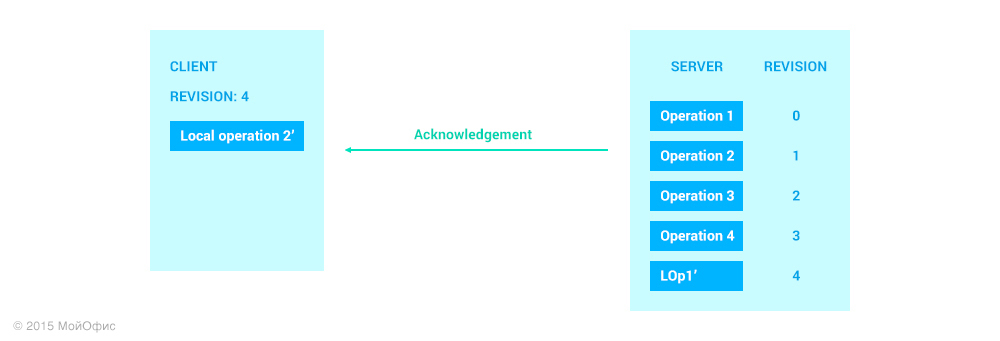
And what happens next with Local Operation 2?

“What happens next with Local Operation 2?” You ask. Everything described above works for the first local operation. Let's see what will happen to the second. Imagine that as soon as a client has added Local Operation 2, we immediately send it to the server. At the same time, it is quite possible that operations between other clients can “wedge in” between these operations on the server:



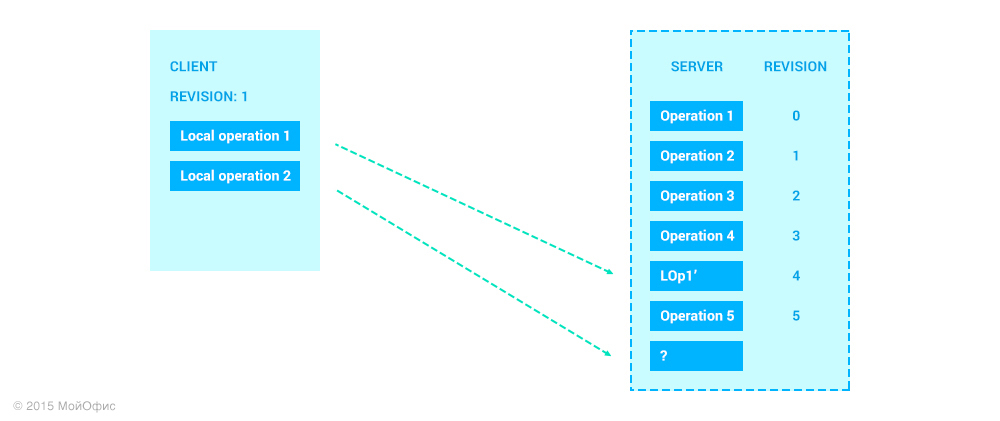
Now, to understand what operation to apply on the server, you need to resolve the following task:



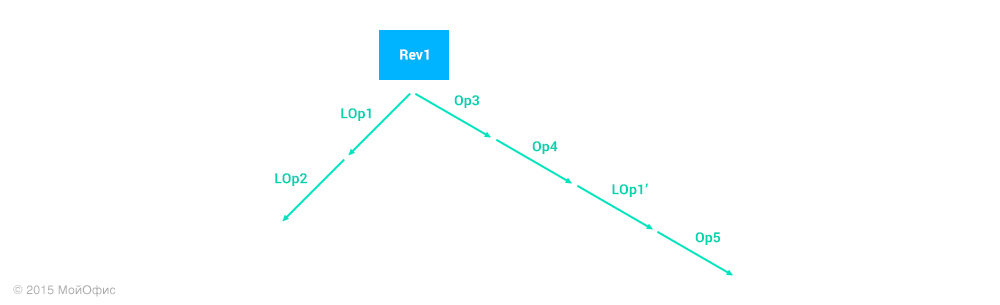
From the point of view of theory, nothing prevents us from doing this. It is enough to apply the transformations mentioned many times to get the necessary operation:



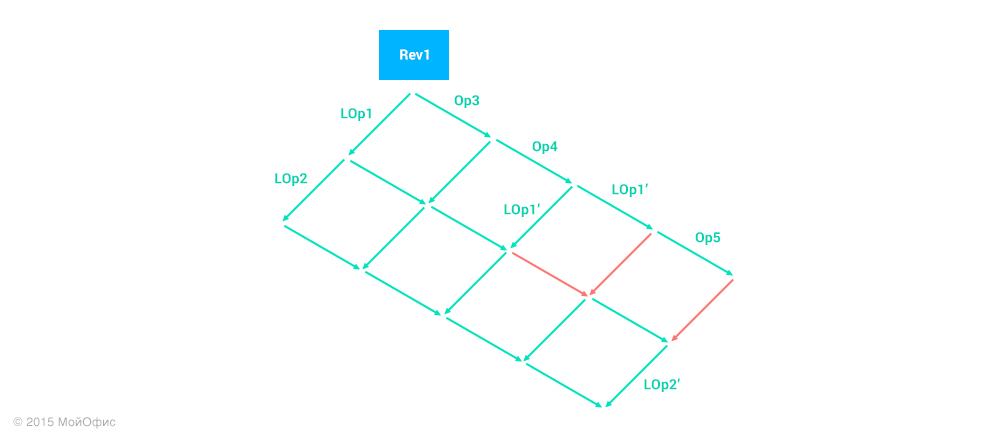
I did not designate all the transformations, otherwise the scheme would be very cumbersome. But It is worth noting that the operations corresponding to the red arrows are empty (identical). This means that the operation LOp2 ′ - these are the changes that we should apply on the server.

Let's look at these calculations from a practical point of view. To perform the transformation data, the server needs to:

1. Know the revision with which the chart starts. There is no difficulty in this, since together with the operation we can send a basic revision.
2. Have information about previous local operations of this client. In the diagram above, this is LOp1, but in general, there can be any number of them. Moreover, it is important to have the status of these operations at the time of sending LOp2, since it was shown above that when the operation comes from the server, local operations will be transformed, which may lead to their change.

The condition “To have information about previous local client operations” means that we need to either send all previous local operations together with LOp2, or restore them using transformations on the server. It is impossible to simply use operations from this client in the history on the server, since they have already undergone transformations. In the first case, network traffic greatly increases, and in the second case, the load on the server increases.

The algorithm, which uses Google Docs and Wave, uses a simple but effective solution that allows you to choose between two evils. The idea is to not send the next local operation until you have received confirmation that the previous one was successfully applied to the server. In our case, this means that LOp2 will be sent only after we received from the server an acknowledgment message related to LOp1:



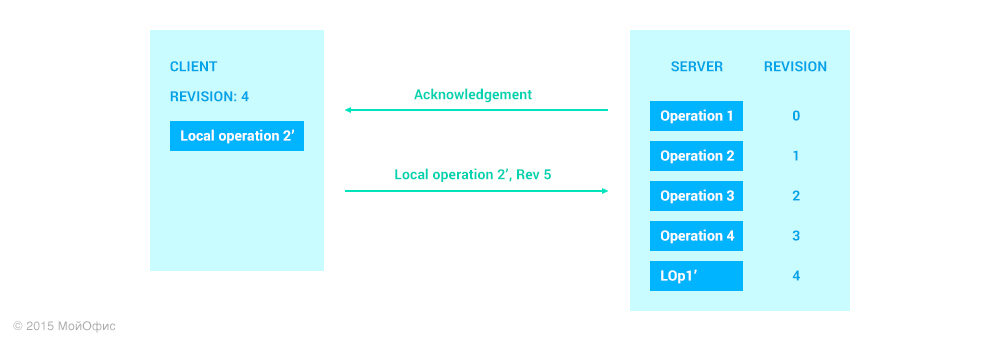
The same approach is used by us.

Total

How these rules work “live” can be seen on the slides.

Undo Editing

The possibility of joint editing makes such an ordinary function, as the cancellation of user actions, very specific. Look at how this should look like from the user.

Suppose we have two people who edit different parts of a document. One of them did not like the last change, and he presses the cancel button. If the system does as the local text editors do — it rolls back the latest change from the history of all edits, then this may well lead to the cancellation of another user’s operation. In this case, both will be confused:

• The one who initiated the cancellation will not see the expected result.
• His colleague will suddenly delete the newly entered text. Well, or appears deleted.

This means that it is appropriate to cancel not the last operation, but the last operation of the user who initiates the cancellation. In this case, the effect will be more expected and close to the usual, which we can observe when editing local documents. Accordingly, each user has its own undo-redo stack.

However, in the history of client operations, the latter may be an operation from another user that he received from the server. Because of this, it becomes impossible to apply the approach to undo-redo, which is used when editing local documents: if you cancel from the stack of operations, the top one gets and rolls back. In our case, we would have to somehow extract the operation from the “middle” of the story and transform all the following:



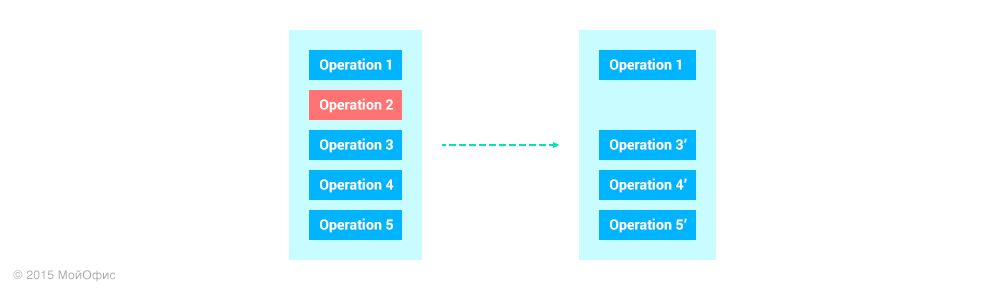
In the algorithm used by us, an important property is that operations that are already coordinated with the server do not change. And if this property is violated, the algorithm will no longer work. So, this principle of cancellation does not suit us.

We need to roll back the operation, which has already plunged into the abyss of history (document operations stack). For this we have only one way: to create a new operation, which will cancel the effect of the original one. We assume that for each operation you can generate the inverse. It is important that the inverse operation can be correctly applied only to the state of the document that occurs immediately after the execution of the original operation.



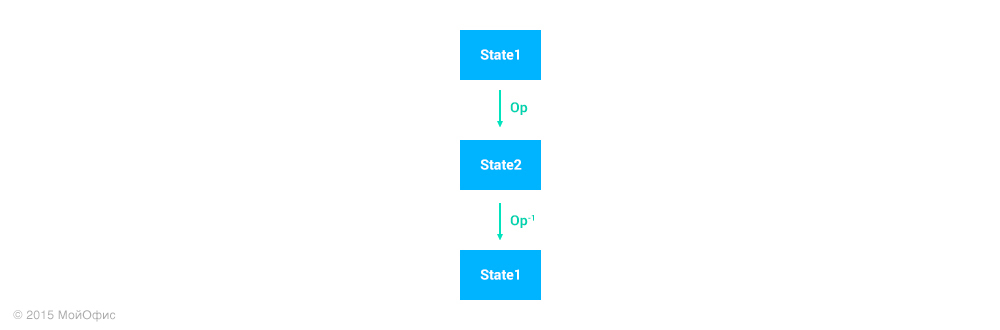
With the help of transformations, we can “transfer” the inverse operation to the current state of the document on the client, as we did before with the corrections:



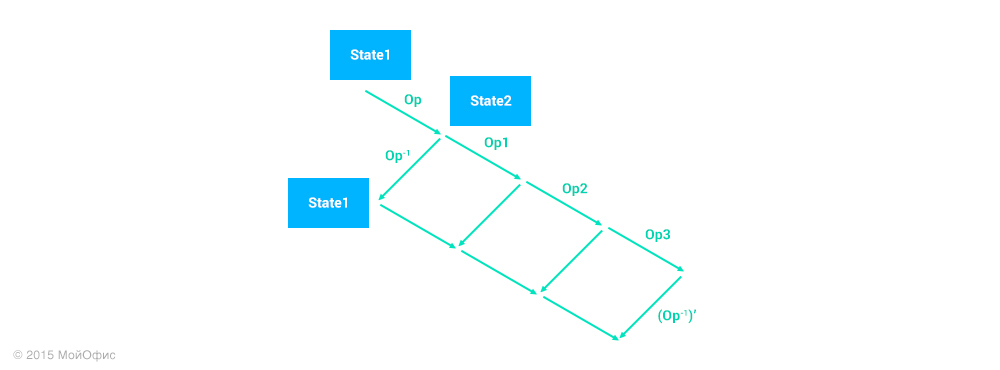
In the diagram (Op ^-1 ) ′, this is just the desired operation. No more changes to the existing algorithm are required: the operation is applied locally and sent to the server like any other. Neither the server nor the other clients can distinguish the undo-operation from the usual one. The information that this was a undo operation is saved only with the user who created it, since it is needed for redo to work correctly.

Practice

In theory, there is no difference between theory and practice.
But, in practice, there is.
Johannes lambertus adriana van de snepscheut

At the moment, we already have an algorithm that allows for non-blocking simultaneous editing with the possibility of canceling operations. At this stage, for the most part theoretical articles it is assumed that the task of constructing an algorithm has been solved. As a “test polygon,” an example is used with editing a single line, where there are only two editing operations: inserting and deleting a character. Sometimes they give an example where a symbol has some property and, accordingly, a third operation appears to change its value. I do not just mention the total number of operations, because we need to be able to transform any of the operations relative to any other, which means for N operations we need to implement N ² transformations. When there are two or three operations, this is not a problem.

To date, the core interface of our product contains more than fifty functions for editing a document. If we represent each of them as a separate operation, then we will have to implement and test more than 2500 transformations, which is simply physically impossible. In addition, we are constantly adding new functionality, so this number continues to grow.

The natural solution in this case is the rejection of a one-to-one correspondence between user actions and operations. The set of operations should be minimal, but so that with the help of a sequence of operations it would be possible to describe any user action. Moreover, if we want to limit the number of operations as much as possible, the operations themselves should be universal. The point is that from the point of view of transformations there is no difference between the operations of setting the font color or its size. Just as there is no difference between inserting a character or inserting a paragraph — everything is inserted into a one-dimensional collection. As a result, it turns out that there will be three fundamentally different operations: inserting an element, deleting and setting an object property.

Products such as CoWord , represent the entire document as a sequential list of different types of elements: letters, carriage translations, pictures, and so on. And for such a model of the document the three proposed operations are enough. But the problem is that this model does not allow to fully present an office document with styles, headers, footers and tables.

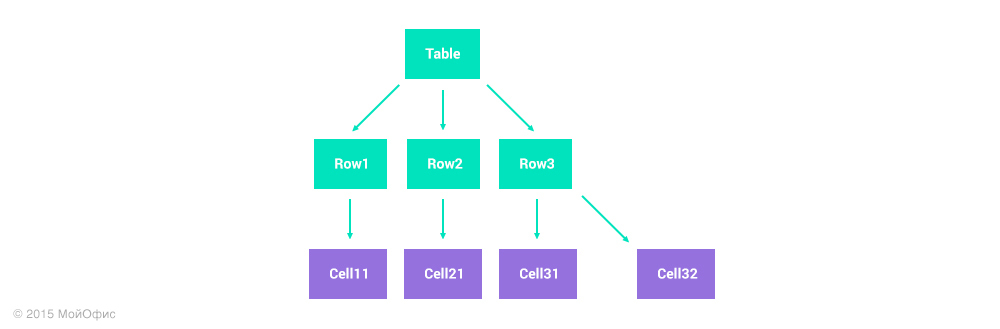
Document as a tree

Instead of a list, it is natural to present the document as a tree, reflecting its hierarchical structure. Simply put, the document in this model looks like this:



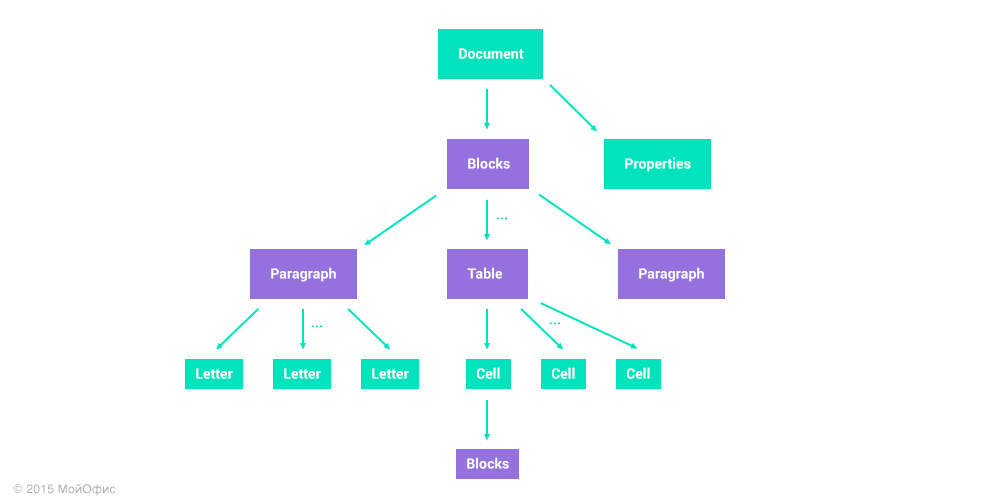
I have deliberately reduced the number of element types to simplify the scheme, but the meaning has been preserved. The document is presented in the form of a tree with two types of nodes:

1. Nodes with a fixed structure are marked in green. As an example, you can take the root element. Any document within this model will always have two child nodes: a list of blocks and a set of properties.
2. Collection nodes that may contain a variable number of child nodes are marked in purple. For example, there may be a different number of blocks (paragraphs or tables) in a document. Similarly, with the letters in the paragraph and the rows and columns in the table.

Having such a document model, you can use the same three primitive operations: insert, delete, and set a property. At the same time, the address of the node in the document tree on which it is executed is added to each operation. For insert or delete operations, this must be the address of the collection; for setting a property, the address of the node for which we want to change this property.

Transformations of tree operations

Addresses of operations help us with transformations. Suppose we have two operations - (Operation1, address1) and (Operation2, address2). We define the effect of the relative position of the nodes on which they are held on the Inc value ((Operation1, address1), (Operation2, address2)). In total there can be four different cases:

1. Nodes are the same, address1 = address2.


.
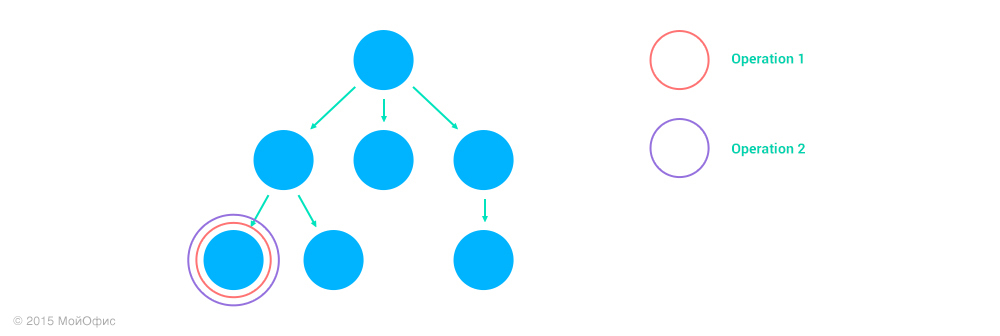
In this case, the transformation takes place as if we had a flat document. The address remains the same:

Inc ((Operation1, address1), (Operation2, address2)) = (Inc (Operation1, Operation2), address1)

2. Operation2 operates on the ancestor of the node Operation1, address2 is the prefix of address1.



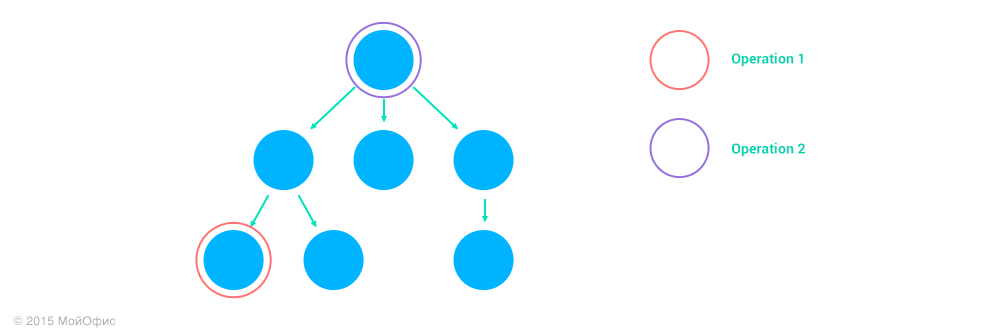
If Operation2 removes the ancestor of the Operation1 node, then as a result we will get an empty operation. If it does not delete, Operation1 itself will not change, but its address may change if Operation2 changes the collection. For example, if Operation1 is the insertion of a character in the second paragraph, and Operation2 is the deletion of the first paragraph, then the result is the insertion of a character with the same index, but in the first paragraph:

Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, Inc (address1, Operation2))

3. Operation1 acts on the ancestor of the node Operation2, address1 is the prefix of address2.



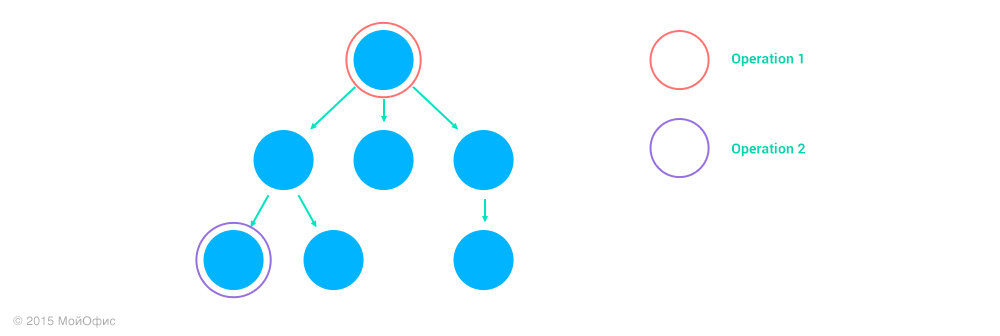
In this case, Operation2 does not affect Operation1:

Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, address1)

4. Operation1 and Operation2 operate on different nodes, none of which is the ancestor of the other.



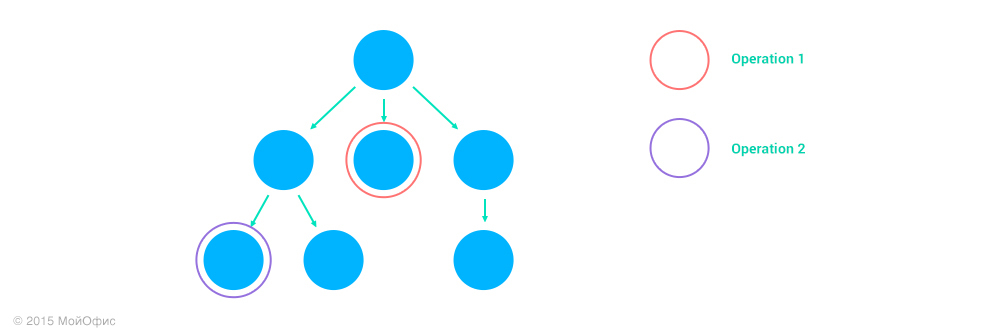
Here, too, the transformation is identical:

Inc ((Operation1, address1), (Operation2, address2)) = (Operation1, address1)

These rules allow us to obtain a transformation for any pair of operations. In addition, operations on various parts of the document will not be transformed, which has a positive effect on performance.

2D collections

Separately worth mentioning the tables. I have seen several publications where authors look at OT above a hierarchical document. However, lists have always been used as collection nodes. When it came to tables, it was said that they can always be defined as a list of rows or columns, which in turn are a list of cells. This approach is fundamentally wrong, since it does not allow for mutually correct transformation of operations on rows and operations on columns. And now I will tell you why.

Imagine that we are storing a 2 by 2 table in the form of a list of rows:



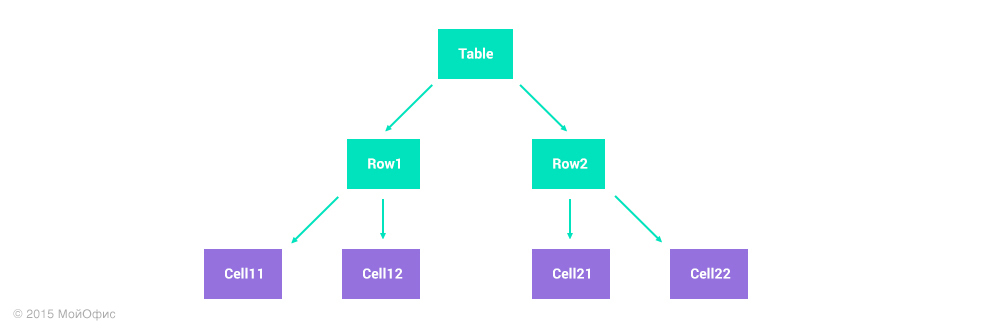
Suppose one user inserts a row at the end of the table, and the second one deletes the right column in parallel. For the first user, its action is described by a single operation: insert (Table, 3, {Cell31, Cell32}). The second will need two operations: remove (Row1, 2), remove (Row2, 2). If we apply all the transformation rules described above, then as a result we will get the following table state:



Either we allow not quite rectangular tables, or we find another approach. We chose the second option. Or rather, they presented the tables as a separate, two-dimensional type of collections. Unlike the list, there may be not two but four operations on them: inserting and deleting columns, and similar for rows. And the address of the child element - the cell - is not a single numerical index, but a pair. This approach allows to correctly represent and transform the operations on rows and columns and prevent situations with the wrong structure of the table.

Conclusion

On this I would like to exhale and write that this is all. For OT, the phrase “the devil is in the details” is incredibly accurate, since the mere trifles turn into the need to solve fundamental problems and complicate the algorithm. Therefore, in the real algorithm of operations on lists, we have not two, but four. And one of them is never satisfied. And the operation can change not only during transformations, but also at the time of execution.

To cover all the nuances in this article is simply not possible, and we will leave them to continue, and we will end the second article.

See you!