We draw on electronic map tiles in MSSQL
I want to tell the readers of the habr community how to use the Microsoft.SqlServer.Types CLR library to create tiles for an electronic map. The article will discuss the generation of a list of cartographic tiles for their further rendering. An algorithm for generating tiles according to the geometry of objects stored in an MS SQL 2008 database will be described. The entire rendering process will be described step by step using the example at the end of the article.

Problem
Initial data
Decision
Tile store
Stages of preparation of tiles
Functions Used
Broken line example
Crossing check
Tile Storage Tables
Placing an icon on a tile
Tile combining
Geometry drawing on tile
Conclusion
When the browser displays a large amount of geo-data in vector graphics (using SVG or CANVAS), sometimes you have to wait not only until the data is uploaded to the client machine, but also until the rendering process takes place, which can take too long.
When displaying a large number of icons on the map in the browser, you can apply clustering, but for complex geometric objects you need to use a different approach.
A set of geometric objects is stored in a Microsoft SQL 2008 database table. Node coordinates are latitude and longitude (EPSG: 4326). The field with geo-data is of type GEOMETRY . Objects should be displayed on the map as an icon for Point geometry. In the form of a broken line of a certain thickness for the geometry of Polyline . Polygon geometry should be displayed as one or more filled polygons with a contour. Tiles must match the projection of the Web Mercator
')
Instead of vector graphics, we will display objects on the map as a raster layer, that is, with the same images (tiles) as the map itself. To do this, it is necessary to prepare a set of map tiles for each scale with the image of objects. For the formation of tiles, we will use the Google Web Mercator projection, that is, the transformation of latitude and longitude to map pixels will be performed using google code, which uses formulas describing the Mercator projection :
Read more about the projection can be read here .
Starting with Sql Server 2008, the GEOMETRY and GEOGRAPHY data types are supported for working with spatial data.
Existing cartographic services from Yandex, Google or OpenStreetMap were provided as cartography in the form of PNG images, of fixed size, usually 256x256 pixels. Although now there are services where tiles are formed using technologies such as SVG or CANVAS. We will consider raster tiles in PNG format (picture network graphic). PNG format supports transparency (indicated in the alpha channel), thanks to which it is possible to overlay the tiles on each other without absolute overlap, when displaying multiple layers.
For each scale a certain set of tiles is stored. For the scale of the 0th level - 1 tile:
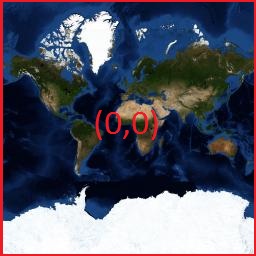
For the scale of the 1st level four tiles 2 * 2:
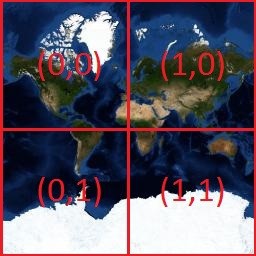
for the scale n, 2n * 2n tiles are stored. The number of tiles with an increase in the scale number increases exponentially.
Tiles are stored in the file system of the Web server and sent to the client’s machine using an http request, for example:
someurl / layer {Z} / {X} / {Y} .png
where Z, X, Y are respectively the scale, X is the position of the tile, Y is the position of the tile. For example, by the following url, a tile with the image of the Trinity Bridge in St. Petersburg is available:
b.tile.openstreetmap.org/15/19144/9524.png
In this url:
15 - scale number;
19144– X tile position;
9524 - Y tile position.
Naturally, in different systems, the URL format of the request is different. Instead of tile numbers and scale, a QUAD-key can be used to request tiles. Tile files can be sent to the client by the server directly from the file system or using http handlers. We will consider the option with X, Y, Z.
To accomplish the task, you will need a function for generating tile geometry by X, Y tile positions and a scale number. The tile geometry in our case is a rectangle covering the tile with the coordinates of the angles expressed in latitude and longitude. The formation of such a geometry can be implemented in the SQL function or in the SQL CLR function. The difference in the runtime of the SQL CLR function and the normal SQL function is not noticeable. The SQL CLR code of the function is implemented in the Coords2PixelConversion class in the attached source codes.
The following geometry is the contour of this tile, that is, passes along its boundaries. The vertex coordinates here are longitude and latitude.
How to use this feature will be discussed later in this article.
Consider the methods of forming a list of tiles. For different geometries, you can choose different approaches to the formation of a list of tiles.
Let us take advantage of this circumstance: If on one scale the object does not intersect with the tile, then on a scale with a large number 4 tiles that overlap the checked tile, they also do not intersect with the object. That is, when going to the next scale, we perform a tile check only if the previous scale tile intersects with the geometry of the object. This eliminates unnecessary checks that are performed in method 2.
In fact, this way - the worst case scenario. For each scale for each object, define a subset of tiles with the GEOMETRY :: STEnvelope () function and check the intersection of the tile from this subset with the object. This method is less effective, especially for objects with a large area or length, since more tiles are checked.
For each object to form the geometry of the tile grid, on the intersection of the grid with the geometry of the object to get a set of points. For each obtained point, define two tiles and add them to the final list of tiles. For example, for a complex geographic line passing through the continent, you can find points of intersection with a grid passing along the borders of the tiles, and from these points you can determine the tiles for rendering. The grid is created within the boundaries of the rectangular area containing the line, and is a set of vertical and horizontal lines. It is much more efficient than checking each tile within the boundaries of a rectangular area of an object.
We describe the first method in more detail. For feature geometries that have an area, a set of tiles for checking intersections with an object can be limited to the extreme tiles of a rectangular area (bbox) that overlaps the object.
According to the geometry of the object (except for the POINT geometry type), a rectangle CLR is formed by the function MSSQL GEOMETRY :: STEnvelope (). For POINT geometry objects, a rectangular area overlapping the object icon on the map is used as the bbox border. The GetImageBound function, which returns a geometry overlapping icon, is implemented in the GoogleProjection class. It also implemented methods for converting latitude and longitude into pixel position numbers. The coordinates of the corner points of a rectangular area are expressed in latitude and longitude. Next we get a subset of tiles covering the resulting rectangle. To do this, we need the function of converting geographic coordinates into a tile number at the appropriate scale. To get the X and Y positions of the tile in longitude and latitude, we can use either the SQL CLR functions, which will be given below, or the SQL functions listed below:
After determining the positions of the corner tiles, all tiles that are in the rectangular area between the corner tiles found are checked for intersection with the geometry of the object in the tile.fn_FetchGeometryTilesZoomDepth () function.
In the tile.fn_FetchGeometryTilesZoomDepth () function, the left upper and right lower tile of the minimum rectangular area covering the geometry is calculated. Then, to determine the intersection of a shape with a tile in a nested loop, we use the tile.fn_GetTilesByTileNumZoomDepth () function for each tile in this area, passing from left to right and from top to bottom from the left top tile to the bottom right one. The function returns a list of tiles for which the intersection with the object's geometry has been defined.
Checking the intersection of the geometry of the tile with the geometry of the object will be a function GEOMETRY :: STIntersects () . If the geometry of the object and the geometry of the tile overlap, then we add an entry to the previously created table tile.TileOverlap and call the same function recursively for the four tiles of the next scale covering the current one, with the @Depth parameter reduced by a unit. The intersection check is implemented in the tile.fn_FetchGeometryTilesZoomDepth () function.
If it is necessary to create tiles for one object, tile numbers can be written directly to the tile.Tile table, since the tile set will be unique. To form a tile with which the geometries of several objects intersect, you need to combine the tiles created for different objects and overlapping each other.
The tile.fn_GetTilesByTileNumZoomDepth () function checks the intersection of object geometry with scale tiles, taking into account the specified depth. The @Depth parameter specifies the check depth, for example, if @Zoom = 2 and @Depth = 1, then a scale 2 tile will be checked, and if there is an intersection, 4 scale tiles 3 will be checked. These tiles must be checked, since they overlap the tile from the previous scale . The intersection check should be performed after converting the GEOMETRY data type to GEOGRAPHY , this is important, since for the GEOGRAPHY data type the check is performed taking into account that all coordinates of geometry points in the 4326 projection, that is, we deal with geometric objects on the sphere.
Suppose we want to get tiles for the broken line connecting the center of St. Petersburg with the center of Moscow. The length of approximately 800 km. Broken will pass through the settlements: Novgorod - Vyshny drap - Tver.
For this geometry from 3 to 17 the scale we get the total of tiles 11076, the distribution of the number of tiles intersecting with the geometry by scales is given in table 1
Tiles obtained for the 3rd and 4th scale are shown in Figure 1:


Figure 1 - Tiles: 3/4/2 and 4/9/4
For each scale, a subset of tiles is formed and each tile is checked without exception. On the 4-5 scale, the number of tiles falling into a rectangular area obtained by the GEOMETRY :: STEnvelope () function on the geometry of the object will be small. The total tiles on the 4 scale are 2 ^ 4 * 2 ^ 4 = 256. But on the 16 and 17 scales it will be necessary to check for many more tiles. The elimination of “extra” checks in the first method will speed up the work. For objects with a point geometry ( POINT ), both methods will have the same efficiency.
The GEOMETRY :: STIntersects () function may not determine the intersection of the object's geometry with the tile geometry, since the STIntersects () function for the GEOMETRY data type works with coordinates on a plane, and the latitude and longitude are not Cartesian coordinates. Therefore, to reliably determine the intersection, we convert the type GEOMETRY into the type GEOGRAPHY . It should be noted that, in contrast to the GEOMETRY data type, the GEOGRAPHY data type requires that the orientation of polygon rings is respected. The coordinates of the outer rings should go counterclockwise. For internal rings (voids), the coordinates should be listed clockwise. To avoid errors in the formation of geography, we use the functions GEOMETRY :: MakeValid () and GEOMETRY :: STUnion () to obtain the correct coordinate sequence, when converting the type GEOMETRY to type GEOGRAPHY. When creating geography, we specify the parameter SRID = 4326, which means that all operations on the coordinates are performed in a spherical system .
At this stage, when the list of tiles is received, that is, a table with three columns: Z, X, Y; Further work can be performed using the mapnik rewriting program , which allows you to create tiles with an image of objects. Organizing mapnik access to a Microsoft SQL Server database requires some effort. Preparation for generating tiles in mapnik includes the following steps:
• Declare the style of objects for rendering;
• Describe the source of data geometry objects;
• Specify a table with a list of tiles for rendering, so as not to generate all the tiles in a row.
We will perform the generation of tiles within the MS SQL Server 2008 database. To do this, you must implement several CLR functions for working with the geometry stored in the database. The main functions that we need are listed below:
Figure 2 shows the structure of the tables, where the list of tiles for rendering is stored. In the Data field in these tables, a PNG image with the image of objects falling on the tile will be saved. Storing and processing a large number of pictures in a table can affect performance. For this task, a more suitable option is to generate tile images outside the database using the list of tiles generated in the table for each object and then saving to the file system.
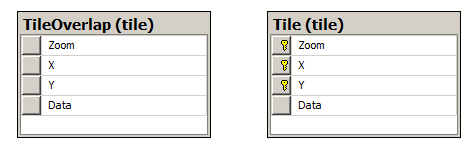
Figure 2 - Tables for storing the list of tiles
Let us analyze the positioning algorithms of the icon on the tile (POINT geometry type).
There is a latitude and longitude of some object, there is a list of tiles of the current scale, on which the icon is superimposed. The formation of the list of tiles was described earlier. The calculation of the position of the icon on the tile consists of the following actions:
1. First, convert latitude and longitude to absolute pixel coordinates;
2. Then, for each tile, from the available list, on the current scale, we calculate the absolute pixel coordinates of the upper left corner. coordinates of the upper left pixel of a tile (pixXtile, pixYtile) are calculated by multiplying the x and y position of the tile by its size, in our case, it is 256 pixels;
3. The difference between the absolute pixel coordinates of the object and the absolute pixel coordinates of the upper-left corner of the tile are defined in the function GetPixelXOnTile () and GetPixelXOnTile (). This difference is the relative pixel coordinates of the center of the icon on the tile;
4. To draw an icon on a tile, you need to get the borders of the drawing area on the tile in pixels, into which the insertion will take place. The relative pixel coordinates of the object on the tile were obtained in the previous step. Now, the size of the icon defines the borders of the rectangular area to be inserted.
5. We draw the icon on the tile.
Icons of several objects can be superimposed on the same tile. To get tiles with all objects, you can first create tiles for each object, then merge them into one. Such a solution can be implemented by grouping rows of a database table; for this purpose, a CLR function has been created to aggregate tile.TileAgg () , which combines tiles into one. This solution has one drawback, since for each object that is intersecting with a tile, we will store a separate record with a BINARY field that stores a tile image, with an election of only this object, which requires a large amount of memory. A better solution is to use one instance of the tile, and consistently display on it all the object icons falling on it. Thus, we spend less memory. In this case, there is simply nothing to group. We want to use grouping.
As the source of the objects we will use the tile.Object table with the coordinates of the objects and the identifier of the image of the icon stored in the tile.Image table in the Binary type field.
For a polyline (POLYLINE, MULTIPOLYLINE), we combine the geometry of the tile with the geometry of the polyline, so part of the polyline is outside the tile area. The algorithm for determining the contour and the region to be painted can be applied to geometries with an area, that is, POLYGON , MULTIPOLYGON , GEOMETRYCOLLECTION containing POLYGON or MULTYPOLYGON . The algorithm is implemented in the ShapeToTileRendering class and includes the following steps:
1. The coordinates (latitude, longitude) of the geometry are converted into pixel coordinates, taking into account the scale by converting the latitude, longitude into PSG3857 pixels (Google projection), and subtracting the coordinates of the upper left pixel of the target tile from each coordinate of the obtained geometry. We obtain the so-called geometry ( A ). These actions are implemented in the function ConvertToZoomedPixelZeroedByTileGeometry (poly, Z, X, Y)
2. The geometry ( B ) of the tile is formed in pixel coordinates, taking into account the scale
3. The geometry ( C ) obtained by the intersection ( STIntersection ) of the pixel geometry of the tile ( B ) with the geometry of the object ( A ) is formed
4. A geometry is formed ( D ) resulting from the intersection of the geometry contour ( C ) and the geometry contour of the tile ( B ), we obtain the lines passing along the border of the tile and bordering with the intended area to be painted over within the tile. Geometry ( E ) resulting from the subtraction is formed using the function .STDifference (other_geometry)
5. Geometry ( E ) is the contour for drawing, which is obtained by subtracting from the contour ( LINESTRING or MULTILINSTRING ) geometry ( C ) geometry ( D ) using the function
6. Filled geometry polygon ( C ) - received filled area
7. The geometry of the ( E ) contour of the polygon is drawn after excluding the intersection with the tile bound
8. Repeat steps 1 through 7 for all tiles of the current object and save them into the tile.TileOverlap table .
3 15- X 19144 Y 9524. T-SQL . , :
:
, . . . , , 6367 . , ( ), , . , . , 360 90 , . , c , . :

, CLR , . .
30.3277587890625, 59.952259717159905 – ;
, :
:
, :
:
( ) 3 , , 4 .
4 –
( D ) , , , 5 , ( ) ( D ), 5.
.
( E ):
5 – ( )
T-SQL PNG Z/X/Y. .
PNG :





DrawPartObjectShapeOnTile() ShapeToTileRendering :
PasteShapeOnTile() .
3-7, , CutPolygonByZoomedPixelZeroTile() , .
GeometryParser «» — X, Y. , :
ShapeToTileRendering CutZoomedPixelPolygonByZeroTile() . . , poly , .
. tile.FillShapeTiles , @GeoData @FolderPath .
CLR :
BitmapFunctions SQL CLR SqlBitmapOperation :
ShapeTile() PNG xTile, yTile:
SqlBitmapOperation TileRendering .
.NET TileRendering .NET :
msdn.microsoft.com/en-us/library/ms345099.aspx
SqlBitmapOperation TileRendering , , :
SqlBitmapOperation nQuant.Core . PNG 8 .
SqlGeometry Microsoft.SqlServer.Types , Microsoft.SqlServer.Types .
System.Drawing – GDI+ c , EXTERNAL_ACCESS , Sytem.Drawing . , EXTERNAL_ACCESS UNSAFE T-SQL :
CLR , , :
ShapeToTileRendering . 4326 . GeometryParser, PSG3857, . PastShapeOnTile , geom . 256 .
tile.FillShapeTiles .
, 100 000 , . . , CLR .
tile.FillShapeTilesIntersection() CLR tile.ShapeTile() .PNG , . CLR . , CLR tile.TileAgg(@Data VARBINARY(MAX)) , .PNG , VABINARY(MAX).
CLR :
tile.FillShapeTilesIntersection tile.Shape. @StartZoom – , @EndZoom — . tile.Shapes.fillArgb tile.Shapes.strokeArgb . : AARRGGBB ,
AA – (), RR – , GG — , BB – . : DDDDFFDD.
, , , . — , . - , SQL Server.
 github
github
3.5

Content
Problem
Initial data
Decision
Tile store
Stages of preparation of tiles
Functions Used
Broken line example
Crossing check
Tile Storage Tables
Placing an icon on a tile
Tile combining
Geometry drawing on tile
Conclusion
Problem
When the browser displays a large amount of geo-data in vector graphics (using SVG or CANVAS), sometimes you have to wait not only until the data is uploaded to the client machine, but also until the rendering process takes place, which can take too long.
When displaying a large number of icons on the map in the browser, you can apply clustering, but for complex geometric objects you need to use a different approach.
Initial data:
A set of geometric objects is stored in a Microsoft SQL 2008 database table. Node coordinates are latitude and longitude (EPSG: 4326). The field with geo-data is of type GEOMETRY . Objects should be displayed on the map as an icon for Point geometry. In the form of a broken line of a certain thickness for the geometry of Polyline . Polygon geometry should be displayed as one or more filled polygons with a contour. Tiles must match the projection of the Web Mercator
')
Decision:
Instead of vector graphics, we will display objects on the map as a raster layer, that is, with the same images (tiles) as the map itself. To do this, it is necessary to prepare a set of map tiles for each scale with the image of objects. For the formation of tiles, we will use the Google Web Mercator projection, that is, the transformation of latitude and longitude to map pixels will be performed using google code, which uses formulas describing the Mercator projection :
Read more about the projection can be read here .
Starting with Sql Server 2008, the GEOMETRY and GEOGRAPHY data types are supported for working with spatial data.
Existing cartographic services from Yandex, Google or OpenStreetMap were provided as cartography in the form of PNG images, of fixed size, usually 256x256 pixels. Although now there are services where tiles are formed using technologies such as SVG or CANVAS. We will consider raster tiles in PNG format (picture network graphic). PNG format supports transparency (indicated in the alpha channel), thanks to which it is possible to overlay the tiles on each other without absolute overlap, when displaying multiple layers.
Tile store
For each scale a certain set of tiles is stored. For the scale of the 0th level - 1 tile:

For the scale of the 1st level four tiles 2 * 2:

for the scale n, 2n * 2n tiles are stored. The number of tiles with an increase in the scale number increases exponentially.
Tiles are stored in the file system of the Web server and sent to the client’s machine using an http request, for example:
someurl / layer {Z} / {X} / {Y} .png
where Z, X, Y are respectively the scale, X is the position of the tile, Y is the position of the tile. For example, by the following url, a tile with the image of the Trinity Bridge in St. Petersburg is available:
b.tile.openstreetmap.org/15/19144/9524.png
In this url:
15 - scale number;
19144– X tile position;
9524 - Y tile position.
Naturally, in different systems, the URL format of the request is different. Instead of tile numbers and scale, a QUAD-key can be used to request tiles. Tile files can be sent to the client by the server directly from the file system or using http handlers. We will consider the option with X, Y, Z.
Stages of preparation of tiles
- Forming a list of tiles by the geometry of each object;
- Generation of tiles for each object;
- Combining tiles to get a unique set;
- Save to file system.
Functions Used
To accomplish the task, you will need a function for generating tile geometry by X, Y tile positions and a scale number. The tile geometry in our case is a rectangle covering the tile with the coordinates of the angles expressed in latitude and longitude. The formation of such a geometry can be implemented in the SQL function or in the SQL CLR function. The difference in the runtime of the SQL CLR function and the normal SQL function is not noticeable. The SQL CLR code of the function is implemented in the Coords2PixelConversion class in the attached source codes.
The following geometry is the contour of this tile, that is, passes along its boundaries. The vertex coordinates here are longitude and latitude.
Tile Border Geometry
'POLYGON ((30.322265625 59.955010262062061, 30.322265625 59.949509172252277, 30.333251953125 59.949509172252277, 30.333251953125 59.955010262062061, 30.322265625 59.955010262062061))' Scalar SQL function code tile.GetTileBounds ()
tile.GetTileBounds(@level int, @x int, @y int) CREATE FUNCTION [tile].[GetTileBounds] (@level int, @x int, @y int) RETURNS geometry AS BEGIN DECLARE @res GEOMETRY = NULL IF @level IS NOT NULL AND @x IS NOT NULL AND @y IS NOT NULL BEGIN DECLARE @n1 FLOAT = PI() - 2.0 * PI() * @y / POWER(2.0, @level); DECLARE @n2 FLOAT = PI() - 2.0 * PI() * (@y + 1) / POWER(2.0, @level); DECLARE @top FLOAT = (180.0 / PI() * ATAN(0.5 * (EXP(@n1) - EXP(-@n1)))); DECLARE @bottom FLOAT = (180.0 / PI() * ATAN(0.5 * (EXP(@n2) - EXP(-@n2)))); DECLARE @tileWidth FLOAT = 360 / CONVERT(float, POWER(2, @level)) DECLARE @left FLOAT = @tileWidth * @x - 180, @right FLOAT = @tileWidth * (@x + 1) - 180 SET @res = geometry::STPolyFromText('POLYGON ((' + LTRIM(STR(@left, 25, 16)) + ' ' + LTRIM(STR(@top, 25, 16)) + ', ' + LTRIM(STR(@left, 25, 16)) + ' ' + LTRIM(STR(@bottom, 25, 16)) + ', ' + LTRIM(STR(@right, 25, 16)) + ' ' + LTRIM(STR(@bottom, 25, 16)) + ', ' + LTRIM(STR(@right, 25, 16)) + ' ' + LTRIM(STR(@top, 25, 16)) + ', ' + LTRIM(STR(@left, 25, 16)) + ' ' + LTRIM(STR(@top, 25, 16)) + '))', 0) END RETURN @res END How to use this feature will be discussed later in this article.
Consider the methods of forming a list of tiles. For different geometries, you can choose different approaches to the formation of a list of tiles.
Method 1:
Let us take advantage of this circumstance: If on one scale the object does not intersect with the tile, then on a scale with a large number 4 tiles that overlap the checked tile, they also do not intersect with the object. That is, when going to the next scale, we perform a tile check only if the previous scale tile intersects with the geometry of the object. This eliminates unnecessary checks that are performed in method 2.
Method 2:
In fact, this way - the worst case scenario. For each scale for each object, define a subset of tiles with the GEOMETRY :: STEnvelope () function and check the intersection of the tile from this subset with the object. This method is less effective, especially for objects with a large area or length, since more tiles are checked.
Method 3:
For each object to form the geometry of the tile grid, on the intersection of the grid with the geometry of the object to get a set of points. For each obtained point, define two tiles and add them to the final list of tiles. For example, for a complex geographic line passing through the continent, you can find points of intersection with a grid passing along the borders of the tiles, and from these points you can determine the tiles for rendering. The grid is created within the boundaries of the rectangular area containing the line, and is a set of vertical and horizontal lines. It is much more efficient than checking each tile within the boundaries of a rectangular area of an object.
We describe the first method in more detail. For feature geometries that have an area, a set of tiles for checking intersections with an object can be limited to the extreme tiles of a rectangular area (bbox) that overlaps the object.
According to the geometry of the object (except for the POINT geometry type), a rectangle CLR is formed by the function MSSQL GEOMETRY :: STEnvelope (). For POINT geometry objects, a rectangular area overlapping the object icon on the map is used as the bbox border. The GetImageBound function, which returns a geometry overlapping icon, is implemented in the GoogleProjection class. It also implemented methods for converting latitude and longitude into pixel position numbers. The coordinates of the corner points of a rectangular area are expressed in latitude and longitude. Next we get a subset of tiles covering the resulting rectangle. To do this, we need the function of converting geographic coordinates into a tile number at the appropriate scale. To get the X and Y positions of the tile in longitude and latitude, we can use either the SQL CLR functions, which will be given below, or the SQL functions listed below:
tile.GetXTilePos((@Longitude FLOAT, @Zoom INT) tile.GetYTilePos((@Latitude FLOAT, @Zoom INT) After determining the positions of the corner tiles, all tiles that are in the rectangular area between the corner tiles found are checked for intersection with the geometry of the object in the tile.fn_FetchGeometryTilesZoomDepth () function.
SQL function to get X tile position for longitude and scale number
CREATE FUNCTION tile.GetXTilePos(@Longitude FLOAT, @Zoom INT) RETURNS INT AS BEGIN DECLARE @D FLOAT,@E FLOAT,@F FLOAT,@G FLOAT, @tileY INT, @tileX INT SET @D = 128 * POWER(2, @Zoom) SET @E = ROUND(@D + @Longitude * 256 / 360 * POWER(2, @Zoom), 0) SET @tileX = Floor(@E / 256); RETURN @tileX END The function of getting the Y position of the tile for latitude and scale number
CREATE FUNCTION tile.GetYTilePos(@Latitude FLOAT, @Zoom INT) RETURNS INT AS BEGIN DECLARE @A FLOAT, @B FLOAT, @C FLOAT, @D FLOAT, @E FLOAT, @F FLOAT, @G FLOAT, @tileY INT SET @D = 128 * POWER(2, @Zoom) SET @A = Sin(PI() / 180 * @Latitude) SET @B = -0.9999 SET @C = 0.9999 IF @A < @B SET @A = @B IF @A > @C SET @A = @C SET @F = @A SET @G = Round(@D + 0.5 * Log((1.0 + @F) / (1.0 - @F)) * (-256) * POWER(2, @Zoom) / (2 * PI()),0) SET @tileY = Floor(@G / 256) RETURN @tileY END In the tile.fn_FetchGeometryTilesZoomDepth () function, the left upper and right lower tile of the minimum rectangular area covering the geometry is calculated. Then, to determine the intersection of a shape with a tile in a nested loop, we use the tile.fn_GetTilesByTileNumZoomDepth () function for each tile in this area, passing from left to right and from top to bottom from the left top tile to the bottom right one. The function returns a list of tiles for which the intersection with the object's geometry has been defined.
The function of getting a set of tiles
CREATE FUNCTION tile.fn_FetchGeometryTilesZoomDepth ( @GeoData GEOMETRY, @Zoom INT, @Depth INT) RETURNS @retTiles TABLE ( Zoom INT, TileX INT, TileY INT) AS BEGIN DECLARE @Left FLOAT, @Right FLOAT, @Top FLOAT, @Bottom FLOAT DECLARE @CurrentXTile INT, @CurrentYTile INT, @Quanttiles INT DECLARE @Envelope GEOMETRY, @RightTop GEOMETRY, @LeftBottom GEOMETRY DECLARE @CurTileGeom GEOMETRY, @res GEOMETRY DECLARE @tiletop FLOAT,@tilebottom FLOAT,@tileleft FLOAT, @tileright FLOAT DECLARE @LeftTilePos INT,@RightTilePos INT,@TopTilePos INT DECLARE @BottomTilePos INT SET @envelope = @GeoData.STEnvelope() SET @RightTop = @envelope.STPointN(3) SET @LeftBottom = @envelope.STPointN(1) SET @Right = @RightTop.STX SET @Left = @LeftBottom.STX SET @Top = @RightTop.STY SET @Bottom = @LeftBottom.STY SET @LeftTilePos = tile.GetXTilePos( @Left,@Zoom) SET @RightTilePos = tile.GetXTilePos( @Right,@Zoom) SET @TopTilePos = tile.GetYTilePos( @Top,@Zoom) SET @BottomTilePos = tile.GetYTilePos( @Bottom,@Zoom) SET @CurrentXTile = @LeftTilePos WHILE @CurrentXTile <= @RightTilePos BEGIN SET @currentYTile = @TopTilePos WHILE @CurrentYTile <= @BottomTilePos BEGIN INSERT INTO @retTiles (Zoom, TileX, TileY) SELECT * FROM tile.fn_GetTilesByTileNumZoomDepth ( @GeoData, @Zoom, @CurrentXTile, @CurrentYTile, @Depth ) SET @CurrentYTile = @CurrentYTile + 1 END SET @CurrentXTile =@CurrentXTile + 1 END RETURN END Checking the intersection of the geometry of the tile with the geometry of the object will be a function GEOMETRY :: STIntersects () . If the geometry of the object and the geometry of the tile overlap, then we add an entry to the previously created table tile.TileOverlap and call the same function recursively for the four tiles of the next scale covering the current one, with the @Depth parameter reduced by a unit. The intersection check is implemented in the tile.fn_FetchGeometryTilesZoomDepth () function.
Retrieving a list of tiles by geometry for the specified tile
CREATE FUNCTION tile.fn_GetTilesByTileNumZoomDepth ( @GeoData GEOMETRY, @Zoom INT, @tileX INT, @tileY INT, @Depth INT) RETURNS @retTiles TABLE ( Zoom INT, X INT, Y INT) AS BEGIN DECLARE @currentTile TABLE ( Zoom INT, X INT, Y INT) IF GEOGRAPHY::STGeomFromWKB([tile].[GetTileBounds](@Zoom, @tileX, @tileY).STAsBinary(),4326).STIntersects(GEOGRAPHY::STGeomFromWKB(@GeoData.MakeValid().STUnion(@GeoData.STStartPoint()).STAsBinary(),4326)) = 1 BEGIN INSERT INTO @currentTile SELECT @Zoom , @tileX , @tileY INSERT INTO @retTiles SELECT d.zoom, dX, dY FROM @currentTile c CROSS APPLY (SELECT * FROM [tile].[fn_GetTilesForObjectByTileNumZoomDepth]( @GeoData , c.Zoom + 1, cX * 2, cY * 2, @Depth - 1) WHERE @Depth > 0) AS d INSERT INTO @retTiles SELECT d.zoom, dX, dY FROM @currentTile c CROSS APPLY (SELECT * FROM [tile].[fn_GetTilesForObjectByTileNumZoomDepth]( @GeoData , c.Zoom + 1, cX * 2 + 1, cY * 2, @Depth - 1) WHERE @Depth > 0) AS d INSERT INTO @retTiles SELECT d.zoom, dX, dY FROM @currentTile c CROSS APPLY (SELECT * FROM [tile].[fn_GetTilesForObjectByTileNumZoomDepth]( @GeoData , c.Zoom + 1, cX * 2, cY * 2 + 1, @Depth - 1) WHERE @Depth > 0) AS d INSERT INTO @retTiles SELECT d.zoom, dX, dY FROM @currentTile c CROSS APPLY (SELECT * FROM [tile].[fn_GetTilesForObjectByTileNumZoomDepth]( @GeoData , c.Zoom + 1, cX * 2 + 1, cY * 2 + 1, @Depth - 1) WHERE @Depth > 0) AS d INSERT INTO @retTiles SELECT * FROM @currentTile END RETURN END If it is necessary to create tiles for one object, tile numbers can be written directly to the tile.Tile table, since the tile set will be unique. To form a tile with which the geometries of several objects intersect, you need to combine the tiles created for different objects and overlapping each other.
The tile.fn_GetTilesByTileNumZoomDepth () function checks the intersection of object geometry with scale tiles, taking into account the specified depth. The @Depth parameter specifies the check depth, for example, if @Zoom = 2 and @Depth = 1, then a scale 2 tile will be checked, and if there is an intersection, 4 scale tiles 3 will be checked. These tiles must be checked, since they overlap the tile from the previous scale . The intersection check should be performed after converting the GEOMETRY data type to GEOGRAPHY , this is important, since for the GEOGRAPHY data type the check is performed taking into account that all coordinates of geometry points in the 4326 projection, that is, we deal with geometric objects on the sphere.
Broken line example
Suppose we want to get tiles for the broken line connecting the center of St. Petersburg with the center of Moscow. The length of approximately 800 km. Broken will pass through the settlements: Novgorod - Vyshny drap - Tver.
Geometry of a broken line from St. Petersburg to Moscow
'LINESTRING( 30.381113 59.971474, 31.26002 58.539215, 34.564158 57.591722, 35.915476 56.876838,37.622242 55.773125)' For this geometry from 3 to 17 the scale we get the total of tiles 11076, the distribution of the number of tiles intersecting with the geometry by scales is given in table 1
Table 1 - Distribution of the number of tiles by scale levels
| Scale | Number of tiles |
|---|---|
| 3 | one |
| four | 2 |
| five | 3 |
| 6 | four |
| 7 | 7 |
| eight | 12 |
| 9 | 23 |
| ten | 45 |
| eleven | 88 |
| 12 | 174 |
| 13 | 347 |
| 14 | 692 |
| 15 | 1383 |
| sixteen | 2766 |
| 17 | 5529 |
Tiles obtained for the 3rd and 4th scale are shown in Figure 1:


Figure 1 - Tiles: 3/4/2 and 4/9/4
For each scale, a subset of tiles is formed and each tile is checked without exception. On the 4-5 scale, the number of tiles falling into a rectangular area obtained by the GEOMETRY :: STEnvelope () function on the geometry of the object will be small. The total tiles on the 4 scale are 2 ^ 4 * 2 ^ 4 = 256. But on the 16 and 17 scales it will be necessary to check for many more tiles. The elimination of “extra” checks in the first method will speed up the work. For objects with a point geometry ( POINT ), both methods will have the same efficiency.
Crossing check
The GEOMETRY :: STIntersects () function may not determine the intersection of the object's geometry with the tile geometry, since the STIntersects () function for the GEOMETRY data type works with coordinates on a plane, and the latitude and longitude are not Cartesian coordinates. Therefore, to reliably determine the intersection, we convert the type GEOMETRY into the type GEOGRAPHY . It should be noted that, in contrast to the GEOMETRY data type, the GEOGRAPHY data type requires that the orientation of polygon rings is respected. The coordinates of the outer rings should go counterclockwise. For internal rings (voids), the coordinates should be listed clockwise. To avoid errors in the formation of geography, we use the functions GEOMETRY :: MakeValid () and GEOMETRY :: STUnion () to obtain the correct coordinate sequence, when converting the type GEOMETRY to type GEOGRAPHY. When creating geography, we specify the parameter SRID = 4326, which means that all operations on the coordinates are performed in a spherical system .
At this stage, when the list of tiles is received, that is, a table with three columns: Z, X, Y; Further work can be performed using the mapnik rewriting program , which allows you to create tiles with an image of objects. Organizing mapnik access to a Microsoft SQL Server database requires some effort. Preparation for generating tiles in mapnik includes the following steps:
• Declare the style of objects for rendering;
• Describe the source of data geometry objects;
• Specify a table with a list of tiles for rendering, so as not to generate all the tiles in a row.
We will perform the generation of tiles within the MS SQL Server 2008 database. To do this, you must implement several CLR functions for working with the geometry stored in the database. The main functions that we need are listed below:
- tile.IconTile (),
- tile.ShapeTile (),
- tile.TileAgg (),
- tile.SaveToFolderByZoomXY ()
Tile Storage Tables
Figure 2 shows the structure of the tables, where the list of tiles for rendering is stored. In the Data field in these tables, a PNG image with the image of objects falling on the tile will be saved. Storing and processing a large number of pictures in a table can affect performance. For this task, a more suitable option is to generate tile images outside the database using the list of tiles generated in the table for each object and then saving to the file system.

Figure 2 - Tables for storing the list of tiles
Placing an icon on a tile
Let us analyze the positioning algorithms of the icon on the tile (POINT geometry type).
There is a latitude and longitude of some object, there is a list of tiles of the current scale, on which the icon is superimposed. The formation of the list of tiles was described earlier. The calculation of the position of the icon on the tile consists of the following actions:
1. First, convert latitude and longitude to absolute pixel coordinates;
2. Then, for each tile, from the available list, on the current scale, we calculate the absolute pixel coordinates of the upper left corner. coordinates of the upper left pixel of a tile (pixXtile, pixYtile) are calculated by multiplying the x and y position of the tile by its size, in our case, it is 256 pixels;
3. The difference between the absolute pixel coordinates of the object and the absolute pixel coordinates of the upper-left corner of the tile are defined in the function GetPixelXOnTile () and GetPixelXOnTile (). This difference is the relative pixel coordinates of the center of the icon on the tile;
4. To draw an icon on a tile, you need to get the borders of the drawing area on the tile in pixels, into which the insertion will take place. The relative pixel coordinates of the object on the tile were obtained in the previous step. Now, the size of the icon defines the borders of the rectangular area to be inserted.
5. We draw the icon on the tile.
CLR SQL function placing the icon on the tile
[Microsoft.SqlServer.Server.SqlFunction] public static SqlBinary IconTile(SqlBinary image, SqlInt32 zoom, SqlDouble Lon, SqlDouble Lat, SqlInt32 xTile, SqlInt32 yTile, SqlDouble scale) { SqlBinary result = null; using (Icon2TileRendering paster = new Icon2TileRendering()) { using (MemoryStream ms = new MemoryStream()) { ms.Write(image.Value, 0, image.Length); SetBeginPosition(ms); paster.PasteFromStreamScaledImageToTile((int)zoom, (double)Lon, (double)Lat, (int)xTile, (int)yTile, (double)scale, ms); result = paster.GetBytes(); } } return result; } Get the bounds of the drawing area
#region [Pixel Position Calculation] Rectangle GetTargetBound(int zoom, double Lon, double Lat, int xTile, int yTile, int width, int height) { int xPix = _conv.FromLongitudeToXPixel(Lon, zoom); int yPix = _conv.FromLatitudeToYPixel(Lat, zoom); int xPos = xPix - xTile * TILE_SIZE; int yPos = yPix - yTile * TILE_SIZE; int halfWidth = width / 2; int halfHeight = height / 2; return new Rectangle(xPos - halfWidth, yPos - halfHeight, width, height } int GetPixelXOnTile(int zoom, double Lon, int xTile) { return _conv.FromLongitudeToXPixel(Lon, zoom) - xTile * TILE_SIZE; } int GetPixelYOnTile(int zoom, double Lat, int yTile) { return _conv.FromLatitudeToYPixel(Lat, zoom) - yTile * TILE_SIZE; } #endregion [Pixel Position Calculation] Copying an icon to a tile
/// <summary> /// /// </summary> /// <param name="zoom"></param> /// <param name="Lon"></param> /// <param name="Lat"></param> /// <param name="xTile"></param> /// <param name="yTile"></param> /// <param name="iconImage"></param> public void PasteImageToTileByLatLon(int zoom, double Lon, double Lat, int xTile, int yTile, Bitmap iconImage) { int width = iconImage.Width; int height = iconImage.Height; CopyRegionIntoImage(iconImage, new Rectangle(0, 0, width, height), GetTargetBound(zoom, Lon, Lat, xTile, yTile, width, height)); } Tile combining
Icons of several objects can be superimposed on the same tile. To get tiles with all objects, you can first create tiles for each object, then merge them into one. Such a solution can be implemented by grouping rows of a database table; for this purpose, a CLR function has been created to aggregate tile.TileAgg () , which combines tiles into one. This solution has one drawback, since for each object that is intersecting with a tile, we will store a separate record with a BINARY field that stores a tile image, with an election of only this object, which requires a large amount of memory. A better solution is to use one instance of the tile, and consistently display on it all the object icons falling on it. Thus, we spend less memory. In this case, there is simply nothing to group. We want to use grouping.
Filling the table with tile positions and tile images with icons drawn on them
CREATE PROC [tile].[FillObjectTilesIntersection]( @StartZoom INT, @EndZoom INT) AS BEGIN DECLARE @CurrentZoom INT SET @CurrentZoom = @StartZoom WHILE @CurrentZoom <= @EndZoom BEGIN INSERT INTO tile.Tile (X,Y,Data,Zoom) SELECT t.TileX,t.TileY, [tile].[TileAgg] (tile.IconTile(i.Data, @CurrentZoom,o.Longitude,o.Latitude,t.tileX,t.tileY, 1.0) ),@CurrentZoom AS Zoom FROM tile.Shape o INNER JOIN tile.[Image] i ON i.ImageID = o.ImageID CROSS APPLY tile.fn_FetchObjectTiles(tile.GetIconBoundForZoom(o.Longitude, o.Latitude, 64, 64, @CurrentZoom, 0),@CurrentZoom) t WHERE o.TypeID = @TypeID GROUP BY t.TileX,t.TileY SET @CurrentZoom = @CurrentZoom + 1 END END As the source of the objects we will use the tile.Object table with the coordinates of the objects and the identifier of the image of the icon stored in the tile.Image table in the Binary type field.
Script of formation of tiles 3/4/2 and 4/9/4 with positioning of the icon at longitude 30.381113 and latitude 59.971474
DECLARE @Image VARBINARY(MAX) SELECT TOP (1) @image = ( SELECT * FROM OPENROWSET(BULK N'd:\media\icons\pin_orange.png', SINGLE_BLOB) As tile) SELECT [tile].[SaveToFolderByZoomXY]([tile].[IconTile](@image, 3,30.381113, 59.971474, 4, 2, 1.0), N'D:\Tiles\',3,4,2) SELECT [tile].[SaveToFolderByZoomXY]([tile].[IconTile](@image, 4,30.381113, 59.971474, 9, 4, 1.0), N'D:\Tiles\',4,9,4) Figure 3 - The resulting tiles with the icon



Geometry drawing on tile
For a polyline (POLYLINE, MULTIPOLYLINE), we combine the geometry of the tile with the geometry of the polyline, so part of the polyline is outside the tile area. The algorithm for determining the contour and the region to be painted can be applied to geometries with an area, that is, POLYGON , MULTIPOLYGON , GEOMETRYCOLLECTION containing POLYGON or MULTYPOLYGON . The algorithm is implemented in the ShapeToTileRendering class and includes the following steps:
1. The coordinates (latitude, longitude) of the geometry are converted into pixel coordinates, taking into account the scale by converting the latitude, longitude into PSG3857 pixels (Google projection), and subtracting the coordinates of the upper left pixel of the target tile from each coordinate of the obtained geometry. We obtain the so-called geometry ( A ). These actions are implemented in the function ConvertToZoomedPixelZeroedByTileGeometry (poly, Z, X, Y)
2. The geometry ( B ) of the tile is formed in pixel coordinates, taking into account the scale
3. The geometry ( C ) obtained by the intersection ( STIntersection ) of the pixel geometry of the tile ( B ) with the geometry of the object ( A ) is formed
4. A geometry is formed ( D ) resulting from the intersection of the geometry contour ( C ) and the geometry contour of the tile ( B ), we obtain the lines passing along the border of the tile and bordering with the intended area to be painted over within the tile. Geometry ( E ) resulting from the subtraction is formed using the function .STDifference (other_geometry)
5. Geometry ( E ) is the contour for drawing, which is obtained by subtracting from the contour ( LINESTRING or MULTILINSTRING ) geometry ( C ) geometry ( D ) using the function
6. Filled geometry polygon ( C ) - received filled area
7. The geometry of the ( E ) contour of the polygon is drawn after excluding the intersection with the tile bound
8. Repeat steps 1 through 7 for all tiles of the current object and save them into the tile.TileOverlap table .
3 15- X 19144 Y 9524. T-SQL . , :
SELECT [tile].[GetTileBounds](15,19144,9524).ToString() :
'POLYGON ((30.322265625 59.955010262062061, 30.322265625 59.949509172252277, 30.333251953125 59.949509172252277, 30.333251953125 59.955010262062061, 30.322265625 59.955010262062061))' , . . . , , 6367 . , ( ), , . , . , 360 90 , . , c , . :
SELECT [tile].[fn_GetCircleSegment](30.3277587890625, 59.952259717159905,0,360,440,90) CREATE FUNCTION [tile].[fn_ GetCircleSegment] (@X float, @Y float, @azimuth float, @angle float, @distance float, @step FLOAT) RETURNS geometry WITH EXEC AS CALLER AS BEGIN IF @X IS NULL OR @Y IS NULL OR @azimuth IS NULL OR ISNULL(@angle, 0) = 0 OR ISNULL(@distance, 0) <= 0 RETURN NULL DECLARE @sectorStepAngle FLOAT SET @sectorStepAngle = @step IF ABS(@angle) > 360 SET @angle = 360 DECLARE @pointsStr VARCHAR(MAX) DECLARE @firstPointsStr VARCHAR(MAX) DECLARE @earthRadius FLOAT DECLARE @lat FLOAT DECLARE @lon FLOAT DECLARE @d FLOAT IF ABS(@angle) < 360 SET @pointsStr = LTRIM(STR(@X, 25, 16)) + ' ' + LTRIM(STR(@Y, 25, 16)) ELSE SET @pointsStr = '' SET @earthRadius = 6367 SET @lat = RADIANS(@Y) SET @lon = RADIANS(@X) SET @d = (@distance / 1000) / @earthRadius DECLARE @angleStart FLOAT DECLARE @angleEnd FLOAT SET @angleStart = @azimuth - @angle / 2; SET @angleEnd = @azimuth + @angle / 2; DECLARE @pointsCount INT SET @pointsCount = FLOOR(@angle / @sectorStepAngle) DECLARE @brng FLOAT DECLARE @latRadians FLOAT DECLARE @lngRadians FLOAT DECLARE @ptX FLOAT DECLARE @ptY FLOAT DECLARE @i INT SET @i = 0 DECLARE @addPrefix TINYINT IF ABS(@angle) < 360 SET @addPrefix = 1 ELSE SET @addPrefix = 0 WHILE @i <= @pointsCount BEGIN SET @brng = RADIANS(@angleStart + @i * @sectorStepAngle); SET @latRadians = ASIN(SIN(@lat) * COS(@d) + COS(@lat) * SIN(@d) * COS(@brng)); SET @lngRadians = @lon + ATN2(SIN(@brng) * SIN(@d) * COS(@lat), COS(@d) - SIN(@lat) * SIN(@latRadians)); SET @ptX = 180.0 * @lngRadians / PI(); SET @ptY = 180.0 * @latRadians / PI(); IF @addPrefix = 1 BEGIN SET @pointsStr += ', ' + LTRIM(STR(@ptX, 25, 16)) + ' ' + LTRIM(STR(@ptY, 25, 16)) END ELSE BEGIN SET @pointsStr += LTRIM(STR(@ptX, 25, 16)) + ' ' + LTRIM(STR(@ptY, 25, 16)) SET @addPrefix = 1 END IF @i = 0 SET @firstPointsStr = LTRIM(STR(@ptX, 25, 16)) + ' ' + LTRIM(STR(@ptY, 25, 16)) IF @i = @pointsCount AND (@angleStart + @pointsCount * @sectorStepAngle) < @angleEnd BEGIN SET @brng = RADIANS(@angleEnd); SET @latRadians = ASIN(SIN(@lat) * COS(@d) + COS(@lat) * SIN(@d) * COS(@brng)); SET @lngRadians = @lon + ATN2(SIN(@brng) * SIN(@d) * COS(@lat), COS(@d) - SIN(@lat) * SIN(@latRadians)); SET @ptX = 180.0 * @lngRadians / PI(); SET @ptY = 180.0 * @latRadians / PI(); SET @pointsStr = @pointsStr + ', ' + LTRIM(STR(@ptX, 25, 16)) + ' ' + LTRIM(STR(@ptY, 25, 16)) END SET @i = @i + 1 END IF ABS(@angle) < 360 SET @pointsStr += ', ' + LTRIM(STR(@X, 25, 16)) + ' ' + LTRIM(STR(@Y, 25, 16)) ELSE SET @pointsStr += ', ' + @firstPointsStr RETURN geometry::STPolyFromText('POLYGON ((' + @pointsStr + '))', 0) END GO , CLR , . .
CLR
/// <summary> /// /// </summary> /// <param name="longitude"></param> /// <param name="latitude"></param> /// <param name="azimuth"></param> /// <param name="angle"></param> /// <param name="radius"></param> /// <returns></returns> [Microsoft.SqlServer.Server.SqlFunction] public static SqlGeometry DrawGeoSpatialSectorVarAngle(SqlDouble longitude, SqlDouble latitude, SqlDouble azimuth, SqlDouble angle, SqlDouble radius, SqlDouble stepAngle) { if (longitude == SqlDouble.Null || latitude == SqlDouble.Null || azimuth == SqlDouble.Null || angle == SqlDouble.Null || radius == SqlDouble.Null || radius == 0 || angle == 0) return SqlGeometry.Parse("GEOMETRYCOLLECTION EMPTY"); SqlGeometryBuilder builder = new SqlGeometryBuilder(); builder.SetSrid(0); builder.BeginGeometry(OpenGisGeometryType.Polygon); double firstPointLon; double firstPointLat; double sectorStepAngle = (double) stepAngle; const double earthRadius = 6367.0; double lat = (double) latitude; double lon = (double) longitude; double azim = (double) azimuth; double ang = (double) angle; double piRad = (Math.PI/180.0); double tLat = piRad*lat; double tLon = piRad*lon; double distkm = ((double) radius/1000)/earthRadius; double angleStart = azim - ang/2; double angleEnd = azim + ang/2; var _angle = Math.Abs(ang); if (_angle > 360.0) { angle = 360.0; } int pointCount = (int) Math.Floor(ang/sectorStepAngle); double brng; double latRadians; double lngRadians; double ptX; double ptY; int i = 0; if (angle < 360.0) { builder.BeginFigure(lon, lat); firstPointLon = lon; firstPointLat = lat; } else { brng = piRad*(angleStart); latRadians = Math.Asin(Math.Sin(tLat)*Math.Cos(distkm) + Math.Cos(tLat)*Math.Sin(distkm)*Math.Cos(brng)); lngRadians = tLon + Math.Atan2(Math.Sin(brng)*Math.Sin(distkm)*Math.Cos(tLat), Math.Cos(distkm) - Math.Sin(tLat)*Math.Sin(latRadians)); ptX = 180.0*lngRadians/Math.PI; ptY = 180.0*latRadians/Math.PI; builder.BeginFigure(ptX, ptY); firstPointLon = ptX; firstPointLat = ptY; } while (i <= pointCount) { brng = piRad*(angleStart + i*sectorStepAngle); latRadians = Math.Asin(Math.Sin(tLat)*Math.Cos(distkm) + Math.Cos(tLat)*Math.Sin(distkm)*Math.Cos(brng)); lngRadians = tLon + Math.Atan2(Math.Sin(brng)*Math.Sin(distkm)*Math.Cos(tLat), Math.Cos(distkm) - Math.Sin(tLat)*Math.Sin(latRadians)); ptX = 180.0*lngRadians/Math.PI; ptY = 180.0*latRadians/Math.PI; builder.AddLine(ptX, ptY); i = i + 1; } if (((angleStart + pointCount * sectorStepAngle) < angleEnd)) { brng = piRad * (angleEnd); latRadians = Math.Asin(Math.Sin(tLat) * Math.Cos(distkm) + Math.Cos(tLat) * Math.Sin(distkm) * Math.Cos(brng)); lngRadians = tLon + Math.Atan2(Math.Sin(brng) * Math.Sin(distkm) * Math.Cos(tLat), Math.Cos(distkm) - Math.Sin(tLat) * Math.Sin(latRadians)); ptX = 180.0 * lngRadians / Math.PI; ptY = 180.0 * latRadians / Math.PI; builder.AddLine(ptX, ptY); } builder.AddLine(firstPointLon, firstPointLat); builder.EndFigure(); builder.EndGeometry(); return builder.ConstructedGeometry; } ()
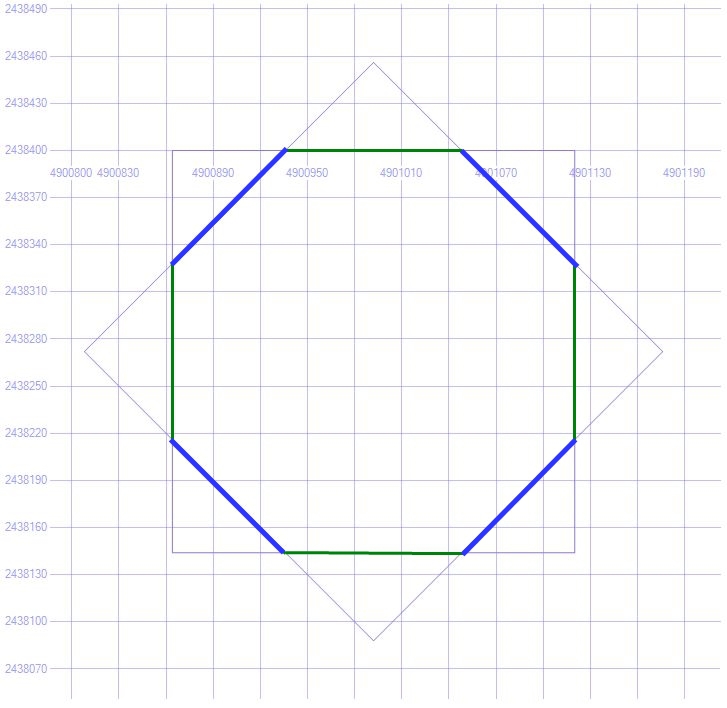
DECLARE @bbox GEOMETRY DECLARE @octagon GEOMETRY SELECT @bbox = [tile].[GetTileBounds](15,19144,9524), @octagon = [tile].[fn_GetCircleSegment](30.3277587890625, 59.952259717159905,0,360,440,90) 30.3277587890625, 59.952259717159905 – ;
, :
SELECT @bbox.STIntersection(@octagon) :
'POLYGON ((30.3253442162734 59.949509172234684, 30.3301733618516 59.949509172234684, 30.333251953125 59.9510505967796, 30.333251953125 59.953468509045528, 30.330173073498937 59.955010262085125, 30.325344504626063 59.955010262085125, 30.322265625 59.953468509045528, 30.322265625 59.9510505967796, 30.3253442162734 59.949509172234684))' , :
X Y
SELECT [tile].[GetPixelXPosFromLongitude](30.3253442162734,15), [tile].[GetPixelYPosFromLatitude](59.949509172234684,15) , [tile].[GetPixelXPosFromLongitude](30.3301733618516,15), [tile].[GetPixelYPosFromLatitude]( 59.949509172234684,15) , [tile].[GetPixelXPosFromLongitude](30.333251953125,15), [tile].[GetPixelYPosFromLatitude]( 59.9510505967796,15) , [tile].[GetPixelXPosFromLongitude](30.333251953125,15), [tile].[GetPixelYPosFromLatitude]( 59.953468509045528,15) , [tile].[GetPixelXPosFromLongitude](30.330173073498937,15), [tile].[GetPixelYPosFromLatitude]( 59.955010262085125,15) , [tile].[GetPixelXPosFromLongitude](30.325344504626063,15), [tile].[GetPixelYPosFromLatitude]( 59.955010262085125,15) ,[tile].[GetPixelXPosFromLongitude](30.322265625,15), [tile].[GetPixelYPosFromLatitude]( 59.953468509045528,15) , [tile].[GetPixelXPosFromLongitude](30.322265625,15), [tile].[GetPixelYPosFromLatitude]( 59.9510505967796,15) , [tile].[GetPixelXPosFromLongitude](30.3253442162734,15), [tile].[GetPixelYPosFromLatitude]( 59.949509172234684,15) | X 15- | Y 15- | ||
|---|---|---|---|
| 30.3253442162734 | 59.949509172234684 | 4900936 | 2438400 |
| 30.3301733618516 | 59.949509172234684 | 4901048 | 2438400 |
| 30.333251953125 | 59.9510505967796 | 4901120 | 2438328 |
| 30.333251953125 | 59.953468509045528 | 4901120 | 2438216 |
| 30.330173073498937 | 59.955010262085125 | 4901048 | 2438144 |
| 30.325344504626063 | 59.955010262085125 | 4900936 | 2438144 |
| 30.322265625 | 59.953468509045528 | 4900864 | 2438216 |
| 30.322265625 | 59.9510505967796 | 4900864 | 2438328 |
| 30.3253442162734 | 59.949509172234684 | 4900936 | 2438400 |
:
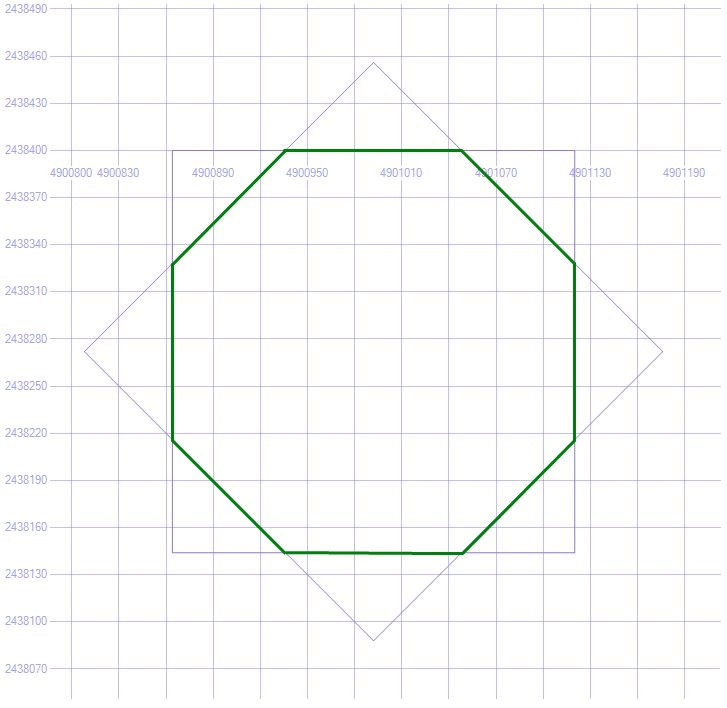
SELECT GEOMETRY::STGeomFromText('LINESTRING(4900936 2438400, 4901048 2438400, 4901120 2438328, 4901120 2438216, 4901048 2438144, 4900936 2438144, 4900864 2438216, 4900864 2438328, 4900936 2438400 )',0) ( ) 3 , , 4 .

4 –
( D ) , , , 5 , ( ) ( D ), 5.
.
( E ):
SELECT GEOMETRY::STGeomFromText('MULTILINESTRING((4901048 2438400, 4901120 2438328),( 4901120 2438216, 4901048 2438144),( 4900936 2438144, 4900864 2438216), (4900864 2438328, 4900936 2438400) )',0) 
5 – ( )
T-SQL PNG Z/X/Y. .
DECLARE @bbox GEOMETRY DECLARE @rhomb GEOMETRY DECLARE @image VARBINARY(MAX) SELECT @bbox = [tile].[GetTileBounds](15,19144,9524), @rhomb = [tile].[fn_GetSector](30.3277587890625, 59.952259717159905,0,360,440,90) SET @image = [tile].[ShapeTile]( @octagon,15,19144,9524,'4400B050','9601B41E',3) SELECT[tile].[SaveToFolderByZoomXY](@image,'d:/tiles',15,19144,9524) SET @image = [tile].[ShapeTile]( @octagon,15,19143,9524,'4400B050','9601B41E',3) SELECT[tile].[SaveToFolderByZoomXY](@image,'d:/tiles',15,19143,9524) SET @image = [tile].[ShapeTile]( @octagon,15,19145,9524,'4400B050','9601B41E',3) SELECT[tile].[SaveToFolderByZoomXY](@image,'d:/tiles',15,19145,9524) SET @image = [tile].[ShapeTile]( @octagon,15,19144,9523,'4400B050','9601B41E',3) SELECT[tile].[SaveToFolderByZoomXY](@image,'d:/tiles',15,19144,9523) SET @image = [tile].[ShapeTile]( @octagon,15,19144,9525,'4400B050','9601B41E',3) SELECT[tile].[SaveToFolderByZoomXY](@image,'d:/tiles',15,19144,9525) PNG :





DrawPartObjectShapeOnTile() ShapeToTileRendering :
/// <summary> /// /// </summary> /// <param name="shape"> </param> /// <param name="X">X </param> /// <param name="Y">Y </param> /// <param name="Zoom"> </param> /// <param name="argbFill"> ARGB</param> /// <param name="argbStroke"> </param> /// <param name="strokeWidth"> </param> public void DrawPartObjectShapeOnTile(SqlGeometry shape, int X, int Y, int Zoom, string argbFill, string argbStroke, int strokeWidth) { PasteShapeOnTile(CreateColor(argbFill), CreateColor(argbStroke), strokeWidth, CutPolygonByZoomedPixelZeroTile(shape, X, Y, Zoom)); } PasteShapeOnTile() .
private void PasteShapeOnTile(Color fillcolor, Color strokecolor, int width, List<SqlGeometry> geom) { SqlGeometry shape = geom[0]; int geomnum = (int) shape.STNumGeometries(); SqlGeometry stroke = null; SqlGeometry ring; int intnum; if (geom != null) switch (GetOpenGisGeometryType(shape)) { case OpenGisGeometryType.LineString: case OpenGisGeometryType.MultiLineString: DrawMultiLineStringBordered2(shape, fillcolor, strokecolor, width, 1); break; case OpenGisGeometryType.Polygon: intnum = (int) shape.STNumInteriorRing(); ring = shape.STExteriorRing(); // 1. FillPolygonOnTile(fillcolor, ring.ToPointsArray()); // 2. if (geomnum >= 1) stroke = geom[1]; for (int i = 1; i <= intnum; i++) { FillTransparentPolygonOnTile(shape.STInteriorRingN(i).ToPointsArray()); } // 3. if (geom.Count > 1) { stroke = geom[1]; DrawContourOnTile(stroke, strokecolor, width); } break; case OpenGisGeometryType.MultiPolygon: break; } } 3-7, , CutPolygonByZoomedPixelZeroTile() , .
/// <summary> /// /// </summary> /// <param name="poly"></param> /// <param name="X"></param> /// <param name="Y"></param> /// <param name="Z"></param> /// <returns> </returns> private List<SqlGeometry> CutPolygonByZoomedPixelZeroTile(SqlGeometry poly, int X, int Y, int Z) { return CutZoomedPixelPolygonByZeroTile(_parser.ConvertToZoomedPixelZeroedByTileGeometry(poly,Z,X,Y); } GeometryParser «» — X, Y. , :
/// <summary /// /// </summary> /// <param name="shape"> </param> /// <param name="zoom"> </param> /// <param name="tileX"> </param> /// <param name="tileY">Y </param> /// <returns> </returns> public SqlGeometry ConvertToZoomedPixelZeroedByTileGeometry(SqlGeometry shape,int zoom, int tileX,int tileY) { return CreateGeometryFromZoomedPixelInfo (ConvertToGeometryZoomedPixelsZeroTileShiftedInfo( GetGeometryInfo(shape), zoom, tileX, tileY)); } /// <summary /// /// </summary> /// <param name="info"> </param> /// <param name="zoom"> </param> /// <param name="x"> </param> /// <param name="y">Y </param> /// <returns> </returns> private GeometryZoomedPixelsInfo ConvertToGeometryZoomedPixelsZeroTileShiftedInfo (GeometryInstanceInfo info, int zoom, int x, int y) { int tilezeroshiftX = x*TILE_SIZE; int tilezeroshiftY = y*TILE_SIZE; var result = new GeometryZoomedPixelsInfo(); var pixelCoordsListList = new List<List<GeometryPixelCoords>>(); var geomPixCoordsList = new List<GeometryPixelCoords>(); var coords = new GeometryPixelCoords {InnerRing = false}; OpenGisGeometryType type = info.ShapeType; result.ShapeType = type; switch (type) { case OpenGisGeometryType.Point: PointF[] geopoints = info.Points[0][0].PointList; coords.PixelCoordList = new[] {new Point{X = _conv.FromLongitudeToXPixel(geopoints[0].X, zoom) - tilezeroshiftX, Y = _conv.FromLatitudeToYPixel(geopoints[0].Y, zoom) - tilezeroshiftY } }; geomPixCoordsList.Add(coords); pixelCoordsListList.Add(geomPixCoordsList); break; case OpenGisGeometryType.LineString: coords.PixelCoordList = GetPixelCoordsShifted( info.Points[0][0].PointList, zoom, tilezeroshiftX, tilezeroshiftY); geomPixCoordsList.Add(coords); pixelCoordsListList.Add(geomPixCoordsList); break; case OpenGisGeometryType.Polygon: foreach (var list in info.Points) foreach (GeometryPointSequence pointseq in list) { coords.PixelCoordList = GetPixelCoordsShifted(pointseq.PointList, zoom, tilezeroshiftX, tilezeroshiftY); coords.InnerRing = pointseq.InnerRing; geomPixCoordsList.Add(coords); } pixelCoordsListList.Add(geomPixCoordsList); break; case OpenGisGeometryType.MultiPoint: case OpenGisGeometryType.MultiLineString: case OpenGisGeometryType.MultiPolygon: pixelCoordsListList = GetGeometryPixelCoordsShifted(info.Points, zoom, tilezeroshiftX, tilezeroshiftY); break; case OpenGisGeometryType.GeometryCollection: GeometryInstanceInfo[] geomColl = info.GeometryInstanceInfoCollection; int n = info.GeometryInstanceInfoCollection.Length; var geomPixZoomInfoCollection = new GeometryZoomedPixelsInfo[n]; for (int i = 0; i < n; i++) { var geom = new GeometryZoomedPixelsInfo(); geom.ShapeType = geomColl[i].ShapeType; geom.Points = GetGeometryPixelCoordsShifted(geomColl[i].Points, zoom, tilezeroshiftX, tilezeroshiftY); geomPixZoomInfoCollection[i] = geom; } result.GeometryInstanceInfoCollection = geomPixZoomInfoCollection; break; } if (type != OpenGisGeometryType.GeometryCollection) result.Points = pixelCoordsListList; return result; } ShapeToTileRendering CutZoomedPixelPolygonByZeroTile() . . , poly , .
private List<SqlGeometry> CutZoomedPixelPolygonByZeroTile(SqlGeometry poly, int X, int Y) { List<SqlGeometry> result = new List<SqlGeometry>(); SqlGeometry stroke = null; SqlGeometry contour; SqlGeometry tileLineString; SqlGeometry tobecut; SqlGeometry tile = _conv.GetTilePixelBound(0, 0, 1); var tiled = poly.STIntersection(tile); result.Add(tiled); switch (GetOpenGisGeometryType(tiled)) { case OpenGisGeometryType.Polygon: // MULTILINESTRING contour = PolygonToMultiLineString(tiled); // tileLineString = tile.ToLineString(); tobecut = contour.STIntersection(tileLineString); stroke = contour.STDifference(tobecut); break; case OpenGisGeometryType.MultiPolygon: // MULTILINESTRING contour = MultiPolygonToMultiLineString(tiled); // tileLineString = tile.ToLineString(); tobecut = contour.STIntersection(tileLineString); stroke = contour.STDifference(tobecut); break; } result.Add(stroke); return result; } . tile.FillShapeTiles , @GeoData @FolderPath .
CLR :
- tile.ShapeTile();
- tile.SaveToFolderByZoomXY()
BitmapFunctions SQL CLR SqlBitmapOperation :
ShapeTile() PNG xTile, yTile:
ShapeTile()
[SqlFunction] public static SqlBinary ShapeTile(SqlGeometry shape, SqlInt32 zoom, SqlInt32 xTile, SqlInt32 yTile, SqlString argbFill,SqlString argbStroke,SqlInt32 strokeWidth) { SqlBinary result = null; using (ShapeToTileRendering paster = new ShapeToTileRendering()) { using (MemoryStream ms = new MemoryStream()) { try { paster.DrawPartObjectShapeOnTile(shape, (int) xTile, (int) yTile, (int) zoom, argbFill.ToString(), argbStroke.ToString(), (int) strokeWidth); result = paster.GetBytes(); } catch (System.Exception ex) { string innerMessage = ex.InnerException.Message; throw new Exception(string.Format("zoom: {1}; X:{2}; Y:{3} {0} , inner: {4}", shape, zoom, xTile,yTile, innerMessage)); } return result; } } } SqlBitmapOperation TileRendering .
.NET TileRendering .NET :
- System
- Microsoft.SqlServer.Types
- System.Drawing
msdn.microsoft.com/en-us/library/ms345099.aspx
SqlBitmapOperation TileRendering , , :
CREATE ASSEMBLY [Microsoft.SqlServer.Types] AUTHORIZATION [dbo] FROM 'd:\SQLCLR\BIN\TileRendering\Microsoft.SqlServer.Types.dll' WITH PERMISSION_SET = UNSAFE GO CREATE ASSEMBLY [System.Drawing] AUTHORIZATION [dbo] FROM 'd:\SQLCLR\BIN\TileRendering\ System.Drawing.dll' WITH PERMISSION_SET = UNSAFE GO CREATE ASSEMBLY [TileRendering] AUTHORIZATION [dbo] FROM 'd:\SQLCLR\BIN\TileRendering\TileRendering.dll' WITH PERMISSION_SET = UNSAFE GO CREATE ASSEMBLY nQuant.Core FROM 'd:\SQLCLR\BIN\TileRendering\ nQuant.Core.dll' WITH PERMISSION_SET = UNSAFE GO CREATE ASSEMBLY SqlBitmapOperation FROM 'd:\SQLCLR\BIN\TileRendering\SqlBitmapOperation.dll' WITH PERMISSION_SET = UNSAFE GO SqlBitmapOperation nQuant.Core . PNG 8 .
SqlGeometry Microsoft.SqlServer.Types , Microsoft.SqlServer.Types .
System.Drawing – GDI+ c , EXTERNAL_ACCESS , Sytem.Drawing . , EXTERNAL_ACCESS UNSAFE T-SQL :
ALTER DATABASE [dataBaseName] SET TRUSTWORTHY ON; CLR , , :
CREATE AGGREGATE [tile].[TileAgg] (@Value [varbinary](max)) RETURNS[varbinary](max) EXTERNAL NAME [SqlBitmapOperation].[TileAgg] GO CREATE AGGREGATE [tile].[IconTileAgg] (@Value [varbinary](max), @PixelX [int], @PixelY [int]) RETURNS[varbinary](max) EXTERNAL NAME [SqlBitmapOperation].[IconTileAgg] GO CREATE FUNCTION [tile].[IconTile](@image [varbinary](max), @zoom [int], @Lon [float], @Lat [float], @xTile [int], @yTile [int], @scale [float]) RETURNS [varbinary](max) WITH EXECUTE AS CALLER AS EXTERNAL NAME [SqlBitmapOperation].[BitmapFunctions].[IconTile] GO --ShapeTile(SqlGeometry shape, SqlInt32 zoom, SqlInt32 xTile, SqlInt32 yTile, SqlString argbFill,SqlString argbStroke,SqlInt32 strokeWidth) CREATE FUNCTION [tile].[ShapeTile](@shape GEOMETRY, @zoom [int], @xTile [int], @yTile [int], @argbFill NVARCHAR(10),@argbStroke NVARCHAR(10), @strokeWidth INT) RETURNS [varbinary](max) WITH EXECUTE AS CALLER AS EXTERNAL NAME [SqlBitmapOperation].[BitmapFunctions].[ShapeTile] GO --SaveToFolderByZoomXY(SqlBinary image, SqlString rootFolderPath, SqlInt32 Zoom, SqlInt32 X,SqlInt32 Y) CREATE FUNCTION tile.SaveToFolderByZoomXY(@image VARBINARY(MAX),@rootFolderPat NVARCHAR(512) , @Zoom [int], @xTile [int], @yTile [int]) RETURNS BIT WITH EXECUTE AS CALLER AS EXTERNAL NAME [SqlBitmapOperation].[BitmapFunctions].[SaveToFolderByZoomXY] GO ShapeToTileRendering . 4326 . GeometryParser, PSG3857, . PastShapeOnTile , geom . 256 .
void PasteShapeOnTile(Color fillcolor,Color strokecolor, int width, List<SqlGeometry> geom) { SqlGeometry shape = geom[0]; int geomnum = (int)shape.STNumGeometries(); SqlGeometry stroke = null; SqlGeometry ring; int intnum; if (geom != null) switch (GetOpenGisGeometryType(shape)) { case OpenGisGeometryType.LineString: case OpenGisGeometryType.MultiLineString: DrawMultiLineStringBordered2(shape, fillcolor, strokecolor, width, 1); break; case OpenGisGeometryType.Polygon: intnum = (int)shape.STNumInteriorRing(); ring = shape.STExteriorRing(); // 1. FillPolygonOnTile(fillcolor, ring.ToPointsArray()); // 2. if (geomnum >= 1) stroke = geom[1]; for (int i = 1; i <= intnum; i++) { FillTransparentPolygonOnTile(shape.STInteriorRingN(i).ToPointsArray()); } // 3. if (geom.Count > 1) { stroke = geom[1]; DrawContourOnTile(stroke, strokecolor, width); } break; case OpenGisGeometryType.MultiPolygon: break; } } tile.FillShapeTiles .
tile.FillShapeTiles
CREATE PROC tile.FillShapeTiles @GeoData GEOMETRY, @fillArgb VARCHAR(20),@strokeArgb VARCHAR(20), @FolderPath NVARCHAR(20), @EndZoom INT = 17, @StartZoom INT = 4, @Thickness INT = 2 AS BEGIN IF @EndZoom < @StartZoom OR @GeoData IS NULL RETURN INSERT INTO tile.tile (Zoom, X,Y,Data) SELECT t.Zoom, t.TileX AS X,t.TileY AS Y, tile.ShapeTile(@GeoData, t.Zoom, t.TileX, t.TileY, @fillArgb, @strokeArgb ,@Thickness) AS Data FROM (SELECT * FROM tile.fn_FetchGeometryTilesZoomDepth(@GeoData,@StartZoom, @EndZoom - @StartZoom)) t SELECT tile.SaveToFolderByZoomXY (Data, @FolderPath ,Zoom,X,Y) FROM tile.Tile END , 100 000 , . . , CLR .
tile.FillShapeTilesIntersection() CLR tile.ShapeTile() .PNG , . CLR . , CLR tile.TileAgg(@Data VARBINARY(MAX)) , .PNG , VABINARY(MAX).
CLR :
- Init();
- Accumulate(value);
- Merge(Agg);
- Terminate()
SQL CLR
//------------------------------------------------------------------------------ // <copyright file="CSSqlAggregate.cs" company="Microsoft"> // Copyright (c) Microsoft Corporation. All rights reserved. // </copyright> //------------------------------------------------------------------------------ using System; using System.Collections.Generic; using System.Data.SqlClient; using System.Data.SqlTypes; using Microsoft.SqlServer.Server; using TileRendering; using System.IO; using System.Drawing; using System.Drawing.Imaging; [Serializable] [SqlUserDefinedAggregate(Format.UserDefined, IsInvariantToDuplicates = true, IsInvariantToNulls = true, IsInvariantToOrder = false, IsNullIfEmpty = false, MaxByteSize = -1)] public struct TileAgg : IBinarySerialize { Bitmap _bitmap; ImageFormat _format; Graphics _graphics; ImageCodecInfo _codecInfo; const int TILE_SIZE = 256; Bitmap GetInitialTile() { Bitmap DrawArea = new Bitmap(TILE_SIZE, TILE_SIZE); using (Graphics xGraph = Graphics.FromImage(DrawArea)) { xGraph.FillRectangle(Brushes.Transparent, 0, 0, TILE_SIZE, TILE_SIZE); _graphics = Graphics.FromImage(DrawArea); return DrawArea; } } #region [Aggregate artifacts] public void Init() { _codecInfo = GetEncoderInfo("image/png"); _bitmap = GetInitialTile(); DetectFormat(); } public void Accumulate(SqlBinary Value) { using (MemoryStream ms = new MemoryStream()) { ms.Write(Value.Value, 0, Value.Length); ms.Seek(0, SeekOrigin.Begin); ms.Position = 0; PasteFromStreamImageToTile( ms); } } public void Merge(TileAgg Group) { PasteGroup(Group.Terminate()); } public SqlBinary Terminate() { return GetBytes(); } #endregion [Aggregate artifacts] void PasteFromStreamImageToTile( Stream stream) { using (Bitmap iconImage = new Bitmap(stream, false)) { DetectFormat(); int width = iconImage.Width; int height = iconImage.Height; var area = new Rectangle(0, 0, width, height); CopyRegionIntoImage(iconImage,area, area); } } void CopyRegionIntoImage(Bitmap srcBitmap, Rectangle srcRegion, Rectangle destRegion) { _graphics.DrawImage(srcBitmap, destRegion, srcRegion, GraphicsUnit.Pixel); srcBitmap.Dispose(); } void PasteGroup(SqlBinary Value) { using (MemoryStream ms = new MemoryStream()) { ms.Write(Value.Value, 0, Value.Length); ms.Seek(0, SeekOrigin.Begin); ms.Position = 0; PasteTile(ms); } } void PasteTile(Stream stream) { Rectangle bounds = new Rectangle(0, 0, TILE_SIZE, TILE_SIZE); CopyRegionIntoImage(new Bitmap(stream), bounds, bounds); } byte[] GetBytes() { return _bitmap.ToByteArray(ImageFormat.Png); } #region [IBinarySerialize] public void Read(BinaryReader reader) { _bitmap = new Bitmap(new MemoryStream(reader.ReadBytes((int)reader.BaseStream.Length))); DetectFormat(); } public void Write(BinaryWriter writer) { EncoderParameters encodeParams = new EncoderParameters(1); encodeParams.Param[0] = new EncoderParameter(System.Drawing.Imaging.Encoder.Quality, 100); _bitmap.Save(writer.BaseStream, _codecInfo, encodeParams); } #endregion [IBinarySerialize] /// <summary> /// /// </summary> void DetectFormat() { _format = _bitmap.GetImageFormat(); } ImageCodecInfo GetEncoderInfo(string mimeType) { // string lookupKey = mimeType.ToLower(); ImageCodecInfo foundCodec = null; Dictionary<string, ImageCodecInfo> encoders = Encoders(); if (encoders.ContainsKey(lookupKey)) { // foundCodec = encoders[lookupKey]; } return foundCodec; } private Dictionary<string, ImageCodecInfo> Encoders() { Dictionary<string, ImageCodecInfo> encoders = new Dictionary<string, ImageCodecInfo>(); foreach (ImageCodecInfo codec in ImageCodecInfo.GetImageEncoders()) { encoders.Add(codec.MimeType.ToLower(), codec); } return encoders; } } tile.FillShapeTilesIntersection tile.Shape. @StartZoom – , @EndZoom — . tile.Shapes.fillArgb tile.Shapes.strokeArgb . : AARRGGBB ,
AA – (), RR – , GG — , BB – . : DDDDFFDD.
CREATE PROC tile.FillShapeTilesIntersection( @StartZoom INT, @EndZoom INT) AS BEGIN DECLARE @Shape GEOMETRY DECLARE @CurrentZoom INT DECLARE @ObjectTypeID INT DECLARE @fillArgb NVARCHAR(10), @strokeArgb NVARCHAR(10) IF @ObjectTypeID IS NOT NULL BEGIN SET @CurrentZoom = @StartZoom DECLARE shape_cursor CURSOR FOR SELECT o.Shape, fillARGB, strokeARGB FROM tile.Shape o OPEN shape_cursor FETCH NEXT FROM shape_cursor INTO @Shape, @fillArgb, @strokeArgb WHILE @@FETCH_STATUS = 0 BEGIN SET @CurrentZoom = @StartZoom WHILE @CurrentZoom <= @EndZoom BEGIN INSERT INTO tile.tileOverlap (Zoom, X,Y,Data) SELECT t.Zoom, t.TileX AS X,t.TileY AS Y, tile.ShapeTile(@Shape, t.Zoom, t.TileX, t.TileY, @fillArgb, @strokeArgb ,2) AS Data FROM (SELECT * FROM tile.fn_FetchGeometryTiles(@Shape,@CurrentZoom)) t SET @CurrentZoom = @CurrentZoom + 1 END FETCH NEXT FROM shape_cursor INTO @Shape, @fillArgb, @strokeArgb END CLOSE shape_cursor; DEALLOCATE shape_cursor; DELETE tile.TileOverlap END END Conclusion
, , , . — , . - , SQL Server.
 github
github3.5
Source: https://habr.com/ru/post/266363/
All Articles