Fourier computations for image comparison
The traditional “entry-level” technique of comparing the current image with the standard is based on considering the images as two-dimensional brightness functions (discrete two-dimensional intensity matrices). In this case, either the distance between the images or the measure of their proximity is measured.
As a rule, to calculate the distances between images, a formula is used which is the sum of the modules or squares of the intensity differences:
If, in addition to simply comparing two images, it is required to solve the problem of finding the position of a fragment of one image in another, then the classical “initial level” method, which consists in enumerating all coordinates and calculating the distance using the specified formula, usually fails due to practical use due to the large number of calculations
One of the methods that can significantly reduce the number of calculations is the use of Fourier transforms and discrete Fourier transforms to calculate the measure of coincidence of two images at different displacements between them. The calculations are performed simultaneously for different combinations of image shifts relative to each other.
')
The presence of a large number of libraries that implement Fourier transforms (in all sorts of variants of the fast versions) makes the implementation of image comparison algorithms not a very difficult task for programming.
For example, find:


According to the definition, the correlation <F, G> of two functions F and G is the value:
This value is well known from the course of mathematics and geometry, devoted to linear spaces, where it is called the scalar product. We will use the formula between the images:
or
This value was obtained from the scalar product operation of vectors (considering images as vectors in multidimensional space). And even more - the same formula is also a standard statistical formula of the criterion for the hypothesis of the coincidence of two probability distributions.
Note:
When calculating the correlation between fragments of images, if one image is smaller than another, we will only divide by the value of the norms of the intersecting parts.
According to the definition, the convolution of two functions F and G is the function FG:
Let G '(t) = G (-t) and F' (t) = F (-t), then, the following equality is obvious:
It is also obvious that FxG '(t) is equal to the correlation of one vector resulting from the shift, relative to the other by step t (this is easy to check by explicit substitution of values in the correlation formula).
The Fourier transform (ℱ) is an operation that associates one function of a real variable with another function, also a real variable. This new function describes the coefficients (“amplitudes”) when decomposing the original function into elementary components — harmonic oscillations with different frequencies.
The Fourier transform of the function f by a real variable is integral and is given by the following formula:
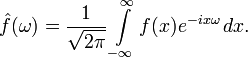
Different sources may give definitions that differ from the above given by choosing the coefficient before the integral, as well as the sign "-" in the exponent. But all the properties will be the same, although the form of some formulas may change.
In addition, there are various generalizations of this concept.
The Fourier transform of functions defined on the space ℝ ^ n is defined by the formula:
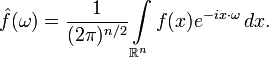
The inverse transformation in this case is given by the formula:
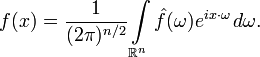
As before, in different sources the definition of a multidimensional Fourier transform may differ by the choice of a constant in front of the integral.
Discrete Fourier transform (in the English-language DFT literature, Discrete Fourier Transform) is one of the Fourier transforms that are widely used in digital signal processing algorithms (its modifications are used in audio compression in MP3, image compression in JPEG, etc.), as well as in other areas associated with the analysis of frequencies in a discrete (for example, digitized analog) signal. The discrete Fourier transform requires a discrete function as an input. Such functions are often created by sampling (sampling values from continuous functions). Discrete Fourier transforms help solve partial differential equations and perform operations such as convolutions. Discrete Fourier transforms are also actively used in statistics when analyzing time series. There are multidimensional discrete Fourier transforms.
Direct conversion:
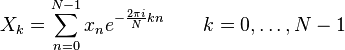
Inverse transform:
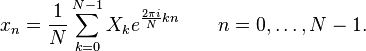
The discrete Fourier transform is a linear transform that translates a vector of time samples into a vector of spectral samples of the same length. Thus, the transformation can be implemented as a multiplication of a symmetric square matrix by a vector:
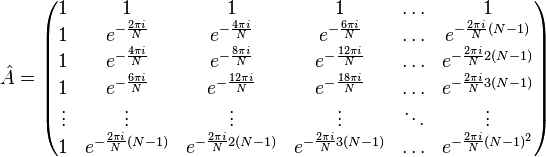
One of the remarkable properties of Fourier transforms is the ability to quickly calculate the correlation of two functions defined, either on a real argument (using the classical formula) or on a finite ring (using discrete transformations).
And although such properties are inherent in many linear transformations, for practical use, to calculate the operation of convolution, according to our definition, the formula is used
Where
It is rather easy to verify the equality of equality by explicitly substituting into formulas of Fourier transforms and reducing the resulting formulas.
Let <F, G> (t) be equal to the correlation of the resulting vector as a result of the shift, relative to the other by step t
Then, as shown earlier,
If implementations of the Fourier transform algorithm through complex numbers are used, such transformations have another remarkable property:
Where CONJUGATE (FFT (G)) is a matrix composed of conjugate elements of the FFT (G) matrix
So we get
When using a formula to estimate the distance between images when shifting (i, j) relative to each other
we get that
Where
When solving a problem for searching for a single sample, the additional rationing of the sample is redundant, and the calculation of the norm for the common part can be replaced by the sum of the pixel brightness in this common part or by the sum of the squares of brightness in this common part
When using a formula to estimate the distance between images when shifting (i, j) relative to each other
we get that
Where
Note:
When using the discrete Fourier transform, the matrix M also contains elements from the cyclic shift of the images between themselves. Therefore, if it is not necessary to analyze the cyclic shift of frames, then the search for the maximum element in the matrix M should be limited to the area (0,0) - (N1-M1, N2-M2).
The implemented algorithms are part of the open source FFTTools library. Internet address: github.com/dprotopopov/FFTTools
Used software
As a rule, to calculate the distances between images, a formula is used which is the sum of the modules or squares of the intensity differences:
d (X, Y) = SUM (X [i, j] - Y [i, j]) ^ 2
If, in addition to simply comparing two images, it is required to solve the problem of finding the position of a fragment of one image in another, then the classical “initial level” method, which consists in enumerating all coordinates and calculating the distance using the specified formula, usually fails due to practical use due to the large number of calculations
One of the methods that can significantly reduce the number of calculations is the use of Fourier transforms and discrete Fourier transforms to calculate the measure of coincidence of two images at different displacements between them. The calculations are performed simultaneously for different combinations of image shifts relative to each other.
')
The presence of a large number of libraries that implement Fourier transforms (in all sorts of variants of the fast versions) makes the implementation of image comparison algorithms not a very difficult task for programming.
Formulation of the problem
- Let two images X and Y be given - an image and a sample, of sizes (N1, N2) and (M1, M2), respectively, and Ni> Mi
- It is required to find the coordinates of the sample Y in the full image X and calculate the estimated value - the measure of proximity.
For example, find:
sample

in the image

Correlation as a measure between images
According to the definition, the correlation <F, G> of two functions F and G is the value:
<F, G> = SUM F (i) * G (i)
This value is well known from the course of mathematics and geometry, devoted to linear spaces, where it is called the scalar product. We will use the formula between the images:
m (X, Y) = SUM (X [i, j] * Y [i, j]) / (SQRT (SUM X [i, j] ^ 2) * SQRT (SUM Y [i, j] ^ 2) )
or
m (X, Y) = <X, Y> / (SQRT (<X, X>) * SQRT (<Y, Y>))
This value was obtained from the scalar product operation of vectors (considering images as vectors in multidimensional space). And even more - the same formula is also a standard statistical formula of the criterion for the hypothesis of the coincidence of two probability distributions.
Note:
When calculating the correlation between fragments of images, if one image is smaller than another, we will only divide by the value of the norms of the intersecting parts.
Convolution of two functions
According to the definition, the convolution of two functions F and G is the function FG:
FxG (t) = SUM F (i) * G (j) | i + j = t
Let G '(t) = G (-t) and F' (t) = F (-t), then, the following equality is obvious:
- FF '(0) = SUM F (i) ^ 2 - scalar product of vector F on itself
- GxG '(0) = SUM G (j) ^ 2– scalar product of vector G on itself
- FxG '(0) = SUM F (i) * G (i) is the scalar product of two vectors F and G
It is also obvious that FxG '(t) is equal to the correlation of one vector resulting from the shift, relative to the other by step t (this is easy to check by explicit substitution of values in the correlation formula).
Fourier transform
The Fourier transform (ℱ) is an operation that associates one function of a real variable with another function, also a real variable. This new function describes the coefficients (“amplitudes”) when decomposing the original function into elementary components — harmonic oscillations with different frequencies.
The Fourier transform of the function f by a real variable is integral and is given by the following formula:
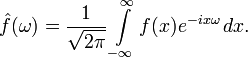
Different sources may give definitions that differ from the above given by choosing the coefficient before the integral, as well as the sign "-" in the exponent. But all the properties will be the same, although the form of some formulas may change.
In addition, there are various generalizations of this concept.
Multidimensional Fourier Transform
The Fourier transform of functions defined on the space ℝ ^ n is defined by the formula:
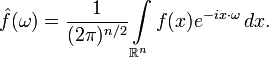
The inverse transformation in this case is given by the formula:
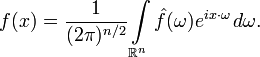
As before, in different sources the definition of a multidimensional Fourier transform may differ by the choice of a constant in front of the integral.
Discrete Fourier Transform
Discrete Fourier transform (in the English-language DFT literature, Discrete Fourier Transform) is one of the Fourier transforms that are widely used in digital signal processing algorithms (its modifications are used in audio compression in MP3, image compression in JPEG, etc.), as well as in other areas associated with the analysis of frequencies in a discrete (for example, digitized analog) signal. The discrete Fourier transform requires a discrete function as an input. Such functions are often created by sampling (sampling values from continuous functions). Discrete Fourier transforms help solve partial differential equations and perform operations such as convolutions. Discrete Fourier transforms are also actively used in statistics when analyzing time series. There are multidimensional discrete Fourier transforms.
Discrete Transform Formulas
Direct conversion:
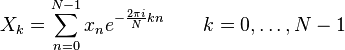
Inverse transform:
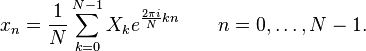
The discrete Fourier transform is a linear transform that translates a vector of time samples into a vector of spectral samples of the same length. Thus, the transformation can be implemented as a multiplication of a symmetric square matrix by a vector:
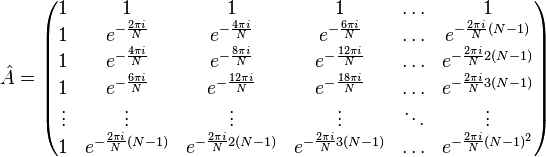
Fourier Transforms for Convolution Calculation
One of the remarkable properties of Fourier transforms is the ability to quickly calculate the correlation of two functions defined, either on a real argument (using the classical formula) or on a finite ring (using discrete transformations).
And although such properties are inherent in many linear transformations, for practical use, to calculate the operation of convolution, according to our definition, the formula is used
FxG = BFT (FFT (F) * FFT (G))
Where
- FFT - direct Fourier transform operation
- BFT is the operation of the inverse Fourier transform
It is rather easy to verify the equality of equality by explicitly substituting into formulas of Fourier transforms and reducing the resulting formulas.
Fourier Transforms for Correlation Calculation
Let <F, G> (t) be equal to the correlation of the resulting vector as a result of the shift, relative to the other by step t
Then, as shown earlier,
<F, G> (t) = FxG '(t) = BFT (FFT (F) * FFT (G'))
If implementations of the Fourier transform algorithm through complex numbers are used, such transformations have another remarkable property:
FFT (G ') = CONJUGATE (FFT (G))
Where CONJUGATE (FFT (G)) is a matrix composed of conjugate elements of the FFT (G) matrix
So we get
<F, G> (t) = BFT (FFT (F) * CONJUGATE (FFT (G)))
Fourier transforms for solving the problem
When using a formula to estimate the distance between images when shifting (i, j) relative to each other
m (X, Y) (i, j) = <X, Y> (i, j) / (| X | (i, j)) * | Y | (i, j)),
we get that
- <X, Y> = XxY '= BFT (FFT (X) * CONJUGATE (FFT (Y)))
- | X | ^ 2 = <X, X> = XxX'xE '= BFT (FFT (X) * CONJUGATE (FFT (X)) * CONJUGATE (FFT (E)) = BFT (SQUAREMAGNITUDE (FFT (X)) * CONJUGATE (FFT (E)))
- | Y | ^ 2 = <Y, Y> = YxY'xE '= BFT (FFT (Y) * CONJUGATE (FFT (Y)) * CONJUGATE (FFT (E)))
Where
- <X, Y> (i, j) is the scalar product of two images obtained by shifting (i, j) relative to each other of images X and Y
- E - image of size equal to the minimum size of X and Y, and filled with single values (that is, the “frame” in which X and Y are compared)
- | X | (i, j) - the norm of the common part of the image X when shifting (i, j)
- | Y | (i, j) - the norm of the common part of the image Y in the shift (i, j)
- FFT is an operation of direct two-dimensional discrete Fourier transform
- BFT is the operation of the inverse two-dimensional discrete Fourier transform
- CONJUGATE - the operation of calculating the matrix of conjugate elements
- SQUAREMAGNITUDE - the operation of calculating the matrix of squares of the amplitudes of the elements
Simplification of formulas for solving the problem
When solving a problem for searching for a single sample, the additional rationing of the sample is redundant, and the calculation of the norm for the common part can be replaced by the sum of the pixel brightness in this common part or by the sum of the squares of brightness in this common part
When using a formula to estimate the distance between images when shifting (i, j) relative to each other
m (X, Y) (i, j) = <X, Y> (i, j) / | X | ^ 2 (i, j),
we get that
- <X, Y> = BFT (FFT (X) * CONJUGATE (FFT (Y)))
- <X, X> = BFT (SQUAREMAGNITUDE (FFT (X)) * CONJUGATE (FFT (E)))
Where
- <X, Y> (i, j) is the scalar product of two images obtained by shifting (i, j) relative to each other of images X and Y
- E - image of size equal to the minimum size of X and Y, and filled with single values (that is, the “frame” in which X and Y are compared)
- <X, X> (i, j) - the norm (the sum of the brightness of the pixels) of the common part of the image X when shifting (i, j)
- FFT is an operation of direct two-dimensional discrete Fourier transform
- BFT is the operation of the inverse two-dimensional discrete Fourier transform
- CONJUGATE - the operation of calculating the matrix of conjugate elements
- SQUAREMAGNITUDE - the operation of calculating the matrix of squares of the amplitudes of the elements
Algorithm for searching a fragment in the full image
- Let two images X and Y be given - an image and a sample, of sizes (N1, N2) and (M1, M2), respectively, and Ni> Mi
- It is required to find the coordinates of the sample Y in the full image X and calculate the estimated value - the measure of proximity.
- Expand the Y image to the size (N1, N2), adding it with zeros
- To form an image E from units of size (M1, M2) and expand to size (N1, N2), adding zeros
- Calculate <X, Y> = BFT (FFT (X) * CONJUGATE (FFT (Y)))
- Calculate <X, X> = BFT (SQUAREMAGNITUDE (FFT (X)) * CONJUGATE (FFT (E)))
- Calculate M [i, j] = (f + <X, Y> [i, j]) / (f + <X, X> [i, j])
- In the matrix M to find the element with the maximum value - the coordinates of this element are the desired position of the sample in the full image, and the value is equal to the evaluation of the measure of comparison.
Note:
When using the discrete Fourier transform, the matrix M also contains elements from the cyclic shift of the images between themselves. Therefore, if it is not necessary to analyze the cyclic shift of frames, then the search for the maximum element in the matrix M should be limited to the area (0,0) - (N1-M1, N2-M2).
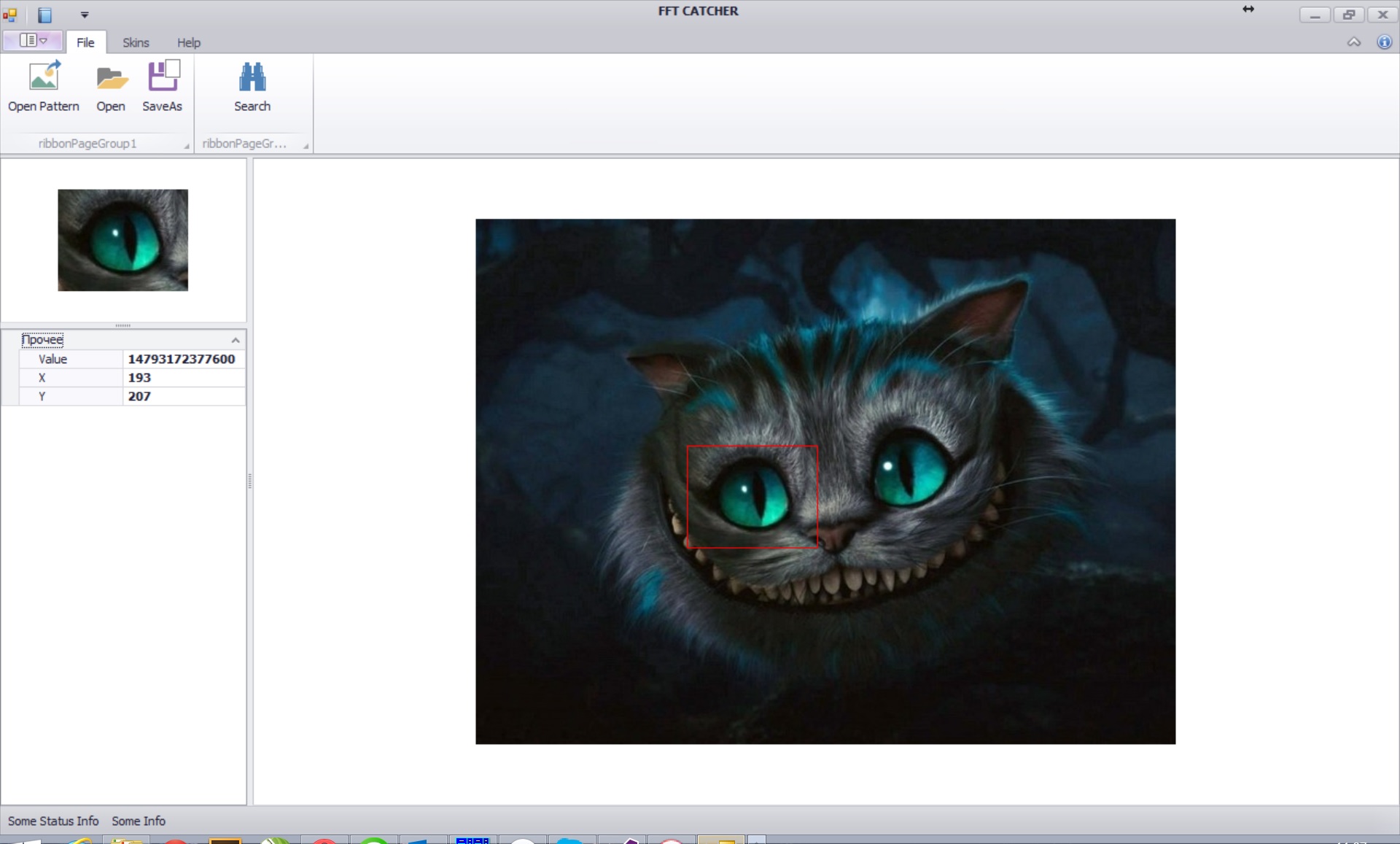
Implementation examples
The implemented algorithms are part of the open source FFTTools library. Internet address: github.com/dprotopopov/FFTTools
Used software
- Microsoft Visual Studio 2013 C # - environment and programming language
- EmguCV / OpenCV - C ++ library of structures and algorithms for image processing
- FFTWSharp / FFTW - C ++ library that implements fast discrete Fourier transform algorithms
/// <summary> /// Catch pattern bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Matrix of values</returns> private Matrix<double> Catch(Image<Gray, double> image) { const double f = 1.0; int length = image.Data.Length; int n0 = image.Data.GetLength(0); int n1 = image.Data.GetLength(1); int n2 = image.Data.GetLength(2); Debug.Assert(n2 == 1); // Allocate FFTW structures var input = new fftw_complexarray(length); var output = new fftw_complexarray(length); fftw_plan forward = fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Forward, fftw_flags.Estimate); fftw_plan backward = fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Backward, fftw_flags.Estimate); var matrix = new Matrix<double>(n0, n1); double[,,] patternData = _patternImage.Data; double[,,] imageData = image.Data; double[,] data = matrix.Data; var doubles = new double[length]; // Calculate Divisor Copy(patternData, data); Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); Complex[] complex = output.GetData_Complex(); Buffer.BlockCopy(imageData, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); input.SetData(output.GetData_Complex().Zip(complex, (x, y) => x*Complex.Conjugate(y)).ToArray()); backward.Execute(); IEnumerable<double> doubles1 = output.GetData_Complex().Select(x => x.Magnitude); if (_fastMode) { // Fast Result Buffer.BlockCopy(doubles1.ToArray(), 0, data, 0, length*sizeof (double)); return matrix; } // Calculate Divider (aka Power) input.SetData(doubles.Select(x => new Complex(x*x, 0)).ToArray()); forward.Execute(); complex = output.GetData_Complex(); CopyAndReplace(_patternImage.Data, data); Buffer.BlockCopy(data, 0, doubles, 0, length*sizeof (double)); input.SetData(doubles.Select(x => new Complex(x, 0)).ToArray()); forward.Execute(); input.SetData(complex.Zip(output.GetData_Complex(), (x, y) => x*Complex.Conjugate(y)).ToArray()); backward.Execute(); IEnumerable<double> doubles2 = output.GetData_Complex().Select(x => x.Magnitude); // Result Buffer.BlockCopy(doubles1.Zip(doubles2, (x, y) => (f + x*x)/(f + y)).ToArray(), 0, data, 0, length*sizeof (double)); return matrix; } /// <summary> /// Copy 3D array to 2D array (sizes can be different) /// Flip copied data /// Reduce last dimension /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> private static void Copy(double[,,] input, double[,] output) { int n0 = output.GetLength(0); int n1 = output.GetLength(1); int m0 = Math.Min(n0, input.GetLength(0)); int m1 = Math.Min(n1, input.GetLength(1)); int m2 = input.GetLength(2); for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] = input[i, j, 0]; for (int k = 1; k < m2; k++) for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] += input[i, j, k]; } /// <summary> /// Copy 3D array to 2D array (sizes can be different) /// Replace items copied by value /// Flip copied data /// Reduce last dimension /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> /// <param name="value">Value to replace copied data</param> private static void CopyAndReplace(double[,,] input, double[,] output, double value = 1.0) { int n0 = output.GetLength(0); int n1 = output.GetLength(1); int m0 = Math.Min(n0, input.GetLength(0)); int m1 = Math.Min(n1, input.GetLength(1)); int m2 = input.GetLength(2); for (int i = 0; i < m0; i++) for (int j = 0; j < m1; j++) output[i, j] = value; } /// <summary> /// Find a maximum element in the matrix /// </summary> /// <param name="matrix">Matrix of values</param> /// <param name="x">Index of maximum element</param> /// <param name="y">Index of maximum element</param> /// <param name="value">Value of maximum element</param> public void Max(Matrix<double> matrix, out int x, out int y, out double value) { double[,] data = matrix.Data; int n0 = data.GetLength(0); int n1 = data.GetLength(1); value = data[0, 0]; x = y = 0; for (int i = 0; i < n0; i++) { for (int j = 0; j < n1; j++) { if (data[i, j] < value) continue; value = data[i, j]; x = j; y = i; } } } /// <summary> /// Catch pattern bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Array of values</returns> public Matrix<double> Catch(Bitmap bitmap) { using (var image = new Image<Gray, Byte>(bitmap)) return Catch(image); } Got that bit

Literature
- A.L. Dmitriev. Optical methods of information processing. Tutorial. SPb. SPUGUITMO 2005. 46 p.
- A.A. Akaev, S..Mayorov “Optical methods of information processing” M.: 1988
- J. Goodman "Introduction to Fourier Optics" M .: Mir 1970
Source: https://habr.com/ru/post/266129/
All Articles