Color Deconvolution at Wolfram Mathematica
I was inspired to write this note by a recent article about monkeys gut . Since the Chukchi is not a reader, the Chukchi is a writer, I decided to try to do this myself. Moreover, the task does not seem complicated and a lot of code is not required.
The simplest algorithm that comes to mind is:
Further, in more detail on each item.
Basic colors are simply the average colors of the image segments. Segmentation algorithms - the sea is bottled, choose to taste, some are implemented in Mathematica . At once I will say that little depends on the choice of the segmentation algorithm, the main thing is that the number of clusters coincide with the desired number of components:
')
Another simple function that we need,
Now the function that returns the basis vectors.
Running ...
And no, wait, not voila. There is no point in decomposing a picture into such basic vectors: the resulting components will more or less repeat the clusters. Here is the moment of truth, i.e. the only inevitable heuristic step. In order for the components of the picture to be more complete, it is necessary to push the base vectors a little bit.
If we want to subtract vector b from vector a and want to keep the components of the vector positive, then the maximum we can do is c = a - min ( a i / b i ) b . In this case, one of the components c will vanish. Naturally, we do not want to push so much. Just subtract the first from the second:
You can, for example, subtract the average vector from all, it does not matter, the main thing is to somehow increase the angle between vectors. Freedom in this step is the inevitable payment for the uncertainty of the task. The coefficient 0 <
The
Base decomposition is a standard procedure. The only subtlety: from the formulation of the problem, it is clear that the coefficients of the decomposition should be positive. The linear span of a set of vectors with positive coefficients is an infinite simplex (a pyramid whose vertex rests on the origin, and the base is carried away to infinity). The edges of this simplex are simplices of smaller dimension. All we need is to project the given vector onto the simplex. If the vector falls inside the simplex (all expansion coefficients over the basis are positive), then the problem is solved, if not, then it is necessary to project on the face.
Here is the whole function:
Checking what works correctly:
Below are comments for those who want to understand the code. The coefficients of the expansion of the vector v in the basis of e (i) are called contravariant coordinates v = v i e (i) . First of all, we calculate the covariant coordinates v i = ( e (i) , v ). If the metric g ij = ( e (i) , e (j) ) is reversible, then the contravariant coordinates are calculated by the inverse metric g ij = ( g −1 ) ij , i.e. v i = g ij v j . That's all. Flag
Although all functions are compiled in C, Mathematica stubbornly does not want to run
First component:
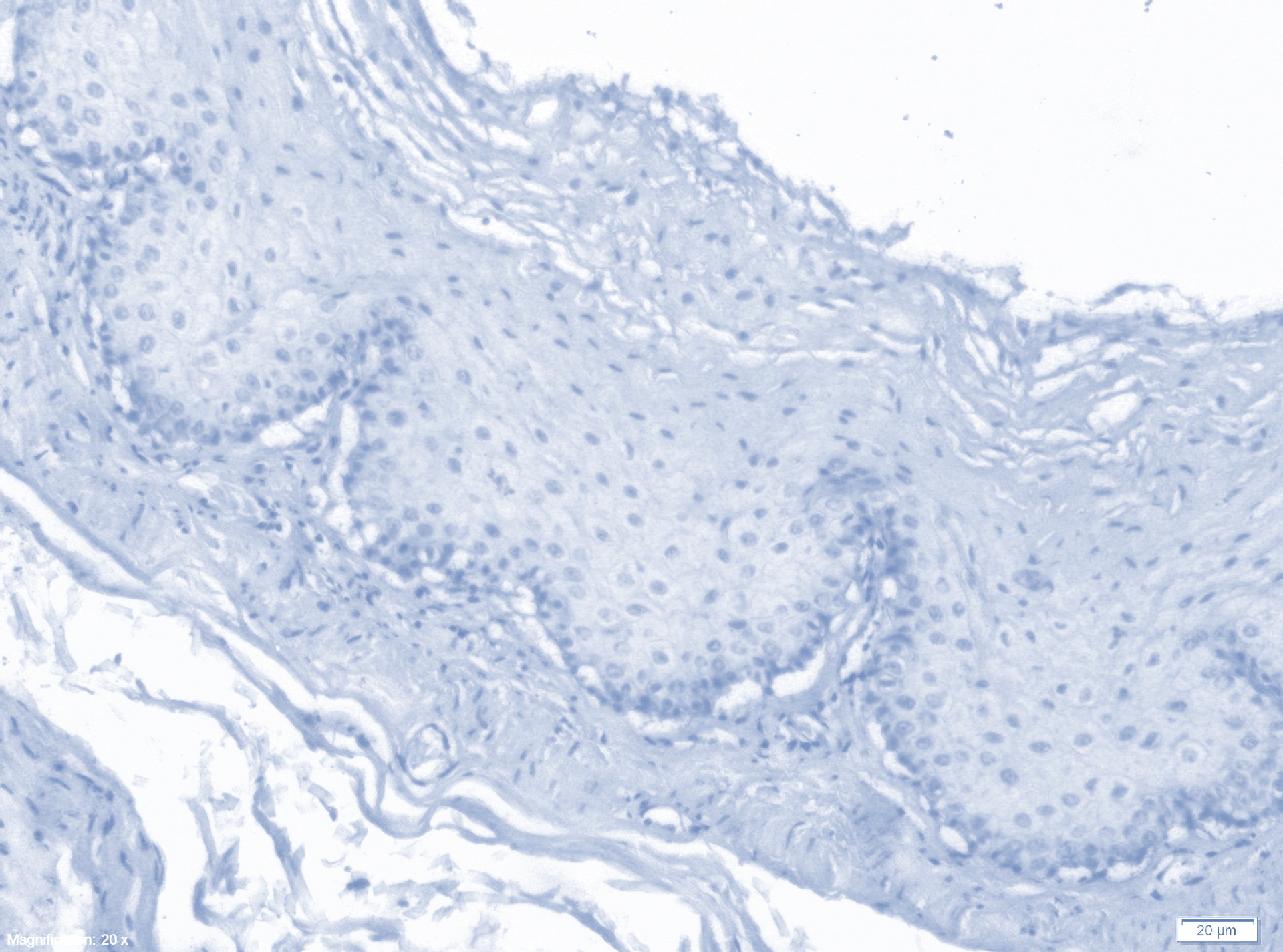
The second component:

Can. Shove in
Download the Mathematica file here .

The simplest algorithm that comes to mind is:
- We define several basic colors of the picture. RGB components of these colors will be used as basis vectors.
- The color of each pixel is decomposed into a linear combination of basic.
- Display an image for each base color.
- Self-esteem automatically rises.
Further, in more detail on each item.
Base colors
Basic colors are simply the average colors of the image segments. Segmentation algorithms - the sea is bottled, choose to taste, some are implemented in Mathematica . At once I will say that little depends on the choice of the segmentation algorithm, the main thing is that the number of clusters coincide with the desired number of components:
')
original = Import["https://hsto.org/files/f42/962/1c5/f429621c55cd46a1beb4d4eb5aefed53.jpg"]; sizeX = First@ImageDimensions[original]; clusters = ClusteringComponents[ original, 3, Method -> "KMeans", DistanceFunction -> CosineDistance ]; Another simple function that we need,
minIndex , returns the position of the minimum element in the list, that is, the compiled substitution Composition[First, Ordering] :not for the sake of truth, but for the sake of truth
minIndex = Compile[ { {list, _Real, 1} }, Module[ { i = 0, min = list[[1]], minPos = 1 }, Do[ If[list[[i]] < min, minPos = i; min = list[[i]]], {i, 1, Length@list} ]; minPos ], CompilationTarget -> "C" ]; Now the function that returns the basis vectors.
removeDarkest removes the darkest color - this is the background, we do not need it: removeDarkest[list_] := Delete[list, minIndex[Norm /@ list]] getBasisColors[image_, clusters_] := Module[ { data = ImageData[image], components = Union[Flatten @ clusters] }, Table[ Median[Join @@ Pick[data, clusters, component]], {component, components} ] ] Running ...
B1 = removeDarkest@getBasisColors[ColorNegate@original, clusters] and voila: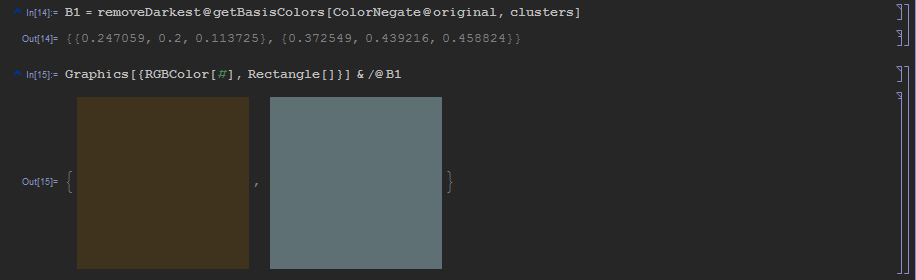
And no, wait, not voila. There is no point in decomposing a picture into such basic vectors: the resulting components will more or less repeat the clusters. Here is the moment of truth, i.e. the only inevitable heuristic step. In order for the components of the picture to be more complete, it is necessary to push the base vectors a little bit.
If we want to subtract vector b from vector a and want to keep the components of the vector positive, then the maximum we can do is c = a - min ( a i / b i ) b . In this case, one of the components c will vanish. Naturally, we do not want to push so much. Just subtract the first from the second:
alpha = 0.5; basis = {B1[[1]], B1[[2]] - alpha Min[B1[[2]]/B1[[1]]] B1[[1]]}; metric = Outer[Dot, basis, basis, 1]; You can, for example, subtract the average vector from all, it does not matter, the main thing is to somehow increase the angle between vectors. Freedom in this step is the inevitable payment for the uncertainty of the task. The coefficient 0 <
alpha <1 is the only fitting parameter of the algorithm. For example, in order to get a picture at the beginning of the post, I had to put alpha = 0.95.The
metric matrix is the metric of the linear envelope of the basis vectors, it is the Gram matrix, which we need in the next section.Basis decomposition
Base decomposition is a standard procedure. The only subtlety: from the formulation of the problem, it is clear that the coefficients of the decomposition should be positive. The linear span of a set of vectors with positive coefficients is an infinite simplex (a pyramid whose vertex rests on the origin, and the base is carried away to infinity). The edges of this simplex are simplices of smaller dimension. All we need is to project the given vector onto the simplex. If the vector falls inside the simplex (all expansion coefficients over the basis are positive), then the problem is solved, if not, then it is necessary to project on the face.
Here is the whole function:
Smooth long only because of my style to write code.
reduceMetric = Compile[ { {metric, _Real, 2}, {index, _Integer} }, Transpose@Delete[Transpose@Delete[metric, index], index], CompilationTarget -> "C" ]; getComponents = Compile[ { {vec, _Real, 1}, {basis, _Real, 2}, {metric, _Real, 2} }, Module[ { covariant, contravariant = Table[0., {Length[basis]}], flag = True, subspace }, covariant = basis.vec; flag = If[ Det[metric] != 0, contravariant = Inverse[metric].covariant; FreeQ[Sign[contravariant], -1], False ]; Chop@If[ flag, contravariant, subspace = Table[ Insert[ getComponents[vec, Delete[basis, i], reduceMetric[metric, i]], 0., i], {i, 1, Length@basis} ]; subspace[[minIndex[-(subspace.covariant)]]] ] ], { {_minIndex, _Integer}, {_reduceMetric, _Real, 2}, {_getComponents, _Real, 1} }, CompilationTarget -> "C", RuntimeAttributes -> {Listable}, Parallelization -> True ] Checking what works correctly:
getComponents[{0.1, 0.9}.basis, basis, metric] {0.1, 0.9} Below are comments for those who want to understand the code. The coefficients of the expansion of the vector v in the basis of e (i) are called contravariant coordinates v = v i e (i) . First of all, we calculate the covariant coordinates v i = ( e (i) , v ). If the metric g ij = ( e (i) , e (j) ) is reversible, then the contravariant coordinates are calculated by the inverse metric g ij = ( g −1 ) ij , i.e. v i = g ij v j . That's all. Flag
flag = False generated in two cases: the metric is irreversible (simplex of a smaller dimension than we thought) or at least one of the contravariant coordinates is negative (did not fall inside the simplex). In these cases, stupidly recursively iterate over all faces, and choose the projection on which is maximum. The projection onto the subspace of the basis e (i) is a convolution of covariant and contravariant coordinates v i v i . Now for sure.results
Although all functions are compiled in C, Mathematica stubbornly does not want to run
getComponents on several cores. Understand laziness, let it remain on the conscience of developers. So just grind all 2736000 pixels: pixels = Join @@ ImageData[ColorNegate@original]; components = Table[ getComponents[pixel, basis, metric], {pixel, pixels} ]; First component:
data1 = (({1, 0} #).basis) & /@ components; ColorNegate[Image@Partition[data1, sizeX]] 
The second component:
data2 = (({0, 1} #).basis) & /@ components; ColorNegate@Image@Partition[data2, sizeX] 
Can I have more?
Can. Shove in
getComponents any, even degenerate / redundant basis, and you will be happy: Module[ { basis = {{1, 0}, {0, 1}, {1, 1}}, metric }, metric = Outer[Dot, basis, basis, 1]; getComponents[{0.1, 0., 0.9}.basis, basis, metric] ] {0.1, 0., 0.9} Download the Mathematica file here .
Source: https://habr.com/ru/post/266101/
All Articles