Error compensation for floating-point operations
The work is devoted to rounding errors that occur when calculating floating-point numbers. The following topics will be briefly discussed here: “Representation of Real Numbers”, “Methods for Finding Round Offsets of Floating Point Numbers” and will give an example of compensation for rounding offsets.
In this paper, examples are given in the programming language C.
Consider the representation of a finite real number in the IEEE 754-2008 standard as an expression, which is characterized by three elements: S (0 or 1), the mantissa M and the order E :
v = -1 S * b (E - BIAS) * M
')
The table below shows the parameters of standard floating-point number formats. Here: w is the width of the bit field to represent the order, t is the width of the bit field to represent the mantissa, k is the full width of the bit string.

The following table shows the ranges of variation and accuracy of standard 32 and 64-bit floating-point real-format formats.
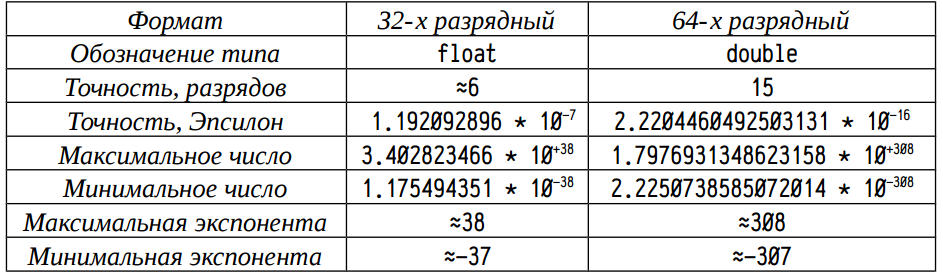
Here "Precision, Epsilon" is the smallest number for which the expression is true:
This Epsilon value characterizes the relative accuracy of the operations of addition and subtraction: if the value added to x or subtracted from x is less than epsilon * x , then the result will remain equal to x . In practice, in some cases, when used in additive operations of quantities approaching in order of epsilon * x , rounding errors of the smaller term begin to affect. About such situations and will be discussed in this work.
Consider the representation of a real number for the float (Binary32) data type.

In this example:
Thus, the number V = 1.01 2 * 2 10 -3 10 = 101 2 * 2 10 -5 10 = 5 10 * 2 10 -5 10 = 0.15625 10
Note that when performing operations with real numbers, often the result will not fit into N-bit Matisses , i.e. rounding will occur. The rounding in one computational operation does not exceed the EPSILON / 2 order, but when we need to do a lot of operations, in order to increase the accuracy of the calculation of the result, we need to learn how to find out exactly how the result of each particular operation is rounded.
For more information about rounding and violation of axiomatics, see makarov_float.pdf (link to the material below).
This problem was investigated by many specialists, the most famous of which are: David Goldberg, William Kakhen, Jonathan Richard Shevchuk.
Below we consider the algorithms for finding rounding errors, given in Shevchuk’s work, using the example of two functions:
For a proper understanding of these algorithms, we will rely on the theorems considered in the work of Shevchuk. Theorems are given without proof.
Saying that the number a is a p -bit number, it means that the length of the Matisse of the number a is represented by p bits.
Theorem: Let the numbers a and b be p- bit floating point numbers, where p > = 3, then following this algorithm we get 2 numbers: x and y , for which the condition is satisfied: a + b = x + y . Moreover, x is an approximation of the sum of a and b , and y is the rounding error of calculating the number x .

In fact, the alogrhythm of finding rounding error when multiplying two real numbers consists of 2 functions: Split — an auxiliary function and TwoProduct function, where we find the error.
Consider the Split function algorithm.
Theorem: the number a is a p -bit floating-point number, where p > = 3. Choose a breakpoint s , where p / 2 <= s <= p -1. Following the algorithm, we obtain ( p - s ) -bit number - the number a_hi and ( s -1) -bit number - a_lo , where | a_hi | > = | a_low | and a = a_hi + a_low .

We now turn to the analysis of the TwoProduct function.
Theorem: Let the numbers a and b be p- bit floating-point numbers, where p > = 6. Then, by performing this algorithm, we get 2 numbers: x and y , for which the condition is satisfied: a * b = x + y . Moreover, x is an approximation of the product of the numbers a and b , and the number y is the rounding error of the calculation of the number x .

It can be seen that the final result is represented by a pair of N-bit real numbers: the result + error. And the second must have an order of no more than EPSILON in relation to the first.
We now turn to practical calculations that are based on Shevchuk's algorithms. Find the rounding errors when adding and multiplying floating-point numbers and analyze how the error accumulates.
Here is an example of the simplest summation program:
As a result of the program, we must get two identical numbers: 2,7892 and 2,7892. But the console was displayed: 2,7892 and 0,0078125. This shows that the error has accumulated very large.
Now we will try to do the same, but using the Shevchuk algorithm, we will accumulate the error in a separate variable, and then we will compensate the result by adding an error to the main variable sum.
As a result, we get 2 numbers: 2,7892 and 0,015625. The result has improved, but the error still makes itself felt. In this example, the error arising in the addition operation was not taken into account in the TwoSum () function:
We will compensate for the result at each iteration of the loop and rewrite the error in the variable that accumulates the rounding error in the summation operation. To do this, we modify the TwoSum () function: we add a isnull variable of the bool type, which indicates whether we should accumulate the error or rewrite it.
As a result, the result will be represented by 2 variables: result - the main variable, error1 - the error of the result operation + = val .
The code will look like this:
The program will display the numbers: 2,7892 and 2,789195.
Note that the rounding error that occurs in the multiplication operation was not taken into account here:
We take this error into account by adding multiplication error accounting functions that were developed by D.R. Shevchuk. In this case, the val variable will be represented by two variables:
Thus, result will be represented by 3 variables: result is the main variable, error1 is the error of the operation result + = val , error2 is the error of the operation of result + = errorMult .
We will also add the error1 and error2 variables , and write the error from this operation into error2 .
As a result, the code:
The following numbers were displayed in the console: 2,7892 and 2,789195.
This suggests that the rounding error of multiplication is small enough to occur even at 10 billion iterations. This result is as close as possible to the original number, if we take into account the errors in the operations of addition and multiplication. To obtain a more accurate result, you can enter additional variables that take into account the errors. Say, add a variable that takes into account the error in the operation of accumulating the main error in the TwoSum () function. Then this error will have the order of EPSILON 2 , in relation to the main result (the first error will have the order of EPSILON ).
We calculate the number 1.0012 101 in the cycle, i.e. do the following:
Note that the exact result, up to the fifteenth decimal place, is 1.128768638496750. We will receive: 1.12876391410828. As you can see, the error was quite large.
Let's output the val variable, casting it to the double data type, and see what is actually written to it:
We get the number 1.00119996070862. This suggests that in programming, even the most accurate constant is neither reliable nor constant. Therefore, our real exact result will be 1.128764164435784, up to the fifteenth decimal place.
Now we will try to improve the result obtained earlier. To do this, we introduce compensation for the result of calculations, by taking into account the rounding error in the multiplication operation. We will also try to add the accumulated error to the result variable at each step.
Code:
The program displays the following number: 1.12876415252686. We got an error of 1.0e-008, which is less than EPSILON / 2 for the float data type . Thus, this result can be considered quite good.
1) In this paper, the presentation of floating-point numbers in the format of IEEE 754-2008 standard was considered.
2) The method of finding rounding errors in the operations of addition and multiplication of floating point numbers was shown.
3) Simple examples of compensation for rounding errors in floating-point numbers were considered.
The work was performed by Victor Fadeev.
Advised Makarov A.The.
PS Thanks for the errors found by users:
xeioex , albom .
In this paper, examples are given in the programming language C.
Representation of real numbers
Consider the representation of a finite real number in the IEEE 754-2008 standard as an expression, which is characterized by three elements: S (0 or 1), the mantissa M and the order E :
v = -1 S * b (E - BIAS) * M
')
- base b (the standard defines three binary formats and two decimal);
- the length of the mantissa p , which determines the accuracy of the representation of a number, is measured in numbers (binary or decimal);
- the maximum value of the order of emax ;
- the minimum value of the order of emin ; The standard requires that the condition be met:
emin = 1-emax - BIAS (offset); order is recorded in the so-called. offset form, i.e.
the real value of the exponent is E-BIAS .
The table below shows the parameters of standard floating-point number formats. Here: w is the width of the bit field to represent the order, t is the width of the bit field to represent the mantissa, k is the full width of the bit string.

The following table shows the ranges of variation and accuracy of standard 32 and 64-bit floating-point real-format formats.

Here "Precision, Epsilon" is the smallest number for which the expression is true:
1 + EPSILON != 1 This Epsilon value characterizes the relative accuracy of the operations of addition and subtraction: if the value added to x or subtracted from x is less than epsilon * x , then the result will remain equal to x . In practice, in some cases, when used in additive operations of quantities approaching in order of epsilon * x , rounding errors of the smaller term begin to affect. About such situations and will be discussed in this work.
Consider the representation of a real number for the float (Binary32) data type.

In this example:
- Number V = 0.15625 10
- The sign S = 0, i.e. +
- Order (E - BIAS) = 01111100 2 - 01111111 2 = 124 10 - 127 10 = -3 10
- Mantissa M = 1.010000000000000000000 2
Thus, the number V = 1.01 2 * 2 10 -3 10 = 101 2 * 2 10 -5 10 = 5 10 * 2 10 -5 10 = 0.15625 10
Note that when performing operations with real numbers, often the result will not fit into N-bit Matisses , i.e. rounding will occur. The rounding in one computational operation does not exceed the EPSILON / 2 order, but when we need to do a lot of operations, in order to increase the accuracy of the calculation of the result, we need to learn how to find out exactly how the result of each particular operation is rounded.
For more information about rounding and violation of axiomatics, see makarov_float.pdf (link to the material below).
Ways of finding rounding errors for floating point numbers
This problem was investigated by many specialists, the most famous of which are: David Goldberg, William Kakhen, Jonathan Richard Shevchuk.
Below we consider the algorithms for finding rounding errors, given in Shevchuk’s work, using the example of two functions:
- TwoSum - the function of finding the rounding error when adding.
- TwoProduct - the function of finding the error of rounding during multiplication.
For a proper understanding of these algorithms, we will rely on the theorems considered in the work of Shevchuk. Theorems are given without proof.
Saying that the number a is a p -bit number, it means that the length of the Matisse of the number a is represented by p bits.
TwoSum
Theorem: Let the numbers a and b be p- bit floating point numbers, where p > = 3, then following this algorithm we get 2 numbers: x and y , for which the condition is satisfied: a + b = x + y . Moreover, x is an approximation of the sum of a and b , and y is the rounding error of calculating the number x .

TwoProduct
In fact, the alogrhythm of finding rounding error when multiplying two real numbers consists of 2 functions: Split — an auxiliary function and TwoProduct function, where we find the error.
Consider the Split function algorithm.
Split
Theorem: the number a is a p -bit floating-point number, where p > = 3. Choose a breakpoint s , where p / 2 <= s <= p -1. Following the algorithm, we obtain ( p - s ) -bit number - the number a_hi and ( s -1) -bit number - a_lo , where | a_hi | > = | a_low | and a = a_hi + a_low .

We now turn to the analysis of the TwoProduct function.
TwoProduct
Theorem: Let the numbers a and b be p- bit floating-point numbers, where p > = 6. Then, by performing this algorithm, we get 2 numbers: x and y , for which the condition is satisfied: a * b = x + y . Moreover, x is an approximation of the product of the numbers a and b , and the number y is the rounding error of the calculation of the number x .

It can be seen that the final result is represented by a pair of N-bit real numbers: the result + error. And the second must have an order of no more than EPSILON in relation to the first.
Example of computation of rounding errors for floating point numbers
We now turn to practical calculations that are based on Shevchuk's algorithms. Find the rounding errors when adding and multiplying floating-point numbers and analyze how the error accumulates.
Amount rounding error
Here is an example of the simplest summation program:
#include <stdio.h> #include <math.h> int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; for (long long i = 0; i < 10000000000; i++) { result += val; } printf("%0.7g \n", result); return 0; } As a result of the program, we must get two identical numbers: 2,7892 and 2,7892. But the console was displayed: 2,7892 and 0,0078125. This shows that the error has accumulated very large.
Now we will try to do the same, but using the Shevchuk algorithm, we will accumulate the error in a separate variable, and then we will compensate the result by adding an error to the main variable sum.
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error) { float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; error += y; return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; float error = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error); } result += error; printf("%0.7g \n", result); return 0; } As a result, we get 2 numbers: 2,7892 and 0,015625. The result has improved, but the error still makes itself felt. In this example, the error arising in the addition operation was not taken into account in the TwoSum () function:
error += y; We will compensate for the result at each iteration of the loop and rewrite the error in the variable that accumulates the rounding error in the summation operation. To do this, we modify the TwoSum () function: we add a isnull variable of the bool type, which indicates whether we should accumulate the error or rewrite it.
As a result, the result will be represented by 2 variables: result - the main variable, error1 - the error of the result operation + = val .
The code will look like this:
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); val = val/10000000000.0; float result = 0.0; float error1 = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error1, false); result = TwoSum(error1, result, error1, true); } printf("%0.7g \n", result); return 0; } The program will display the numbers: 2,7892 and 2,789195.
Note that the rounding error that occurs in the multiplication operation was not taken into account here:
val = val*(1/10000000000.0); We take this error into account by adding multiplication error accounting functions that were developed by D.R. Shevchuk. In this case, the val variable will be represented by two variables:
val_real = val + errorMult Thus, result will be represented by 3 variables: result is the main variable, error1 is the error of the operation result + = val , error2 is the error of the operation of result + = errorMult .
We will also add the error1 and error2 variables , and write the error from this operation into error2 .
As a result, the code:
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { //isNull , // float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } void Split(float a, int s, float& a_hi, float& a_lo) { float c = (pow(2, s) + 1)*a; float a_big = c - a; a_hi = c - a_big; a_lo = a - a_hi; } float TwoProduct(float a, float b, float& err) { float x = a*b; float a_hi, a_low, b_hi, b_low; Split(a, 12, a_hi, a_low); Split(b, 12, b_hi, b_low); float err1, err2, err3; err1 = x - (a_hi*b_hi); err2 = err1 - (a_low*b_hi); err3 = err2 - (a_hi*b_low); err += ((a_low * b_low) - err3); return x; } int main() { float val = 2.7892; printf("%0.7g \n", val); float errorMult = 0;// val = TwoProduct(val, 1.0/10000000000.0, errorMult); float result = 0.0; float error1 = 0.0; float error2 = 0.0; for (long long i = 0; i < 10000000000; i++) { result = TwoSum(result, val, error1, false); result = TwoSum(result, errorMult, error2, false); error1 = TwoSum(error2, error1, error2, true); result = TwoSum(error1, result, error1, true); } printf("%0.7g \n", result); return 0; } The following numbers were displayed in the console: 2,7892 and 2,789195.
This suggests that the rounding error of multiplication is small enough to occur even at 10 billion iterations. This result is as close as possible to the original number, if we take into account the errors in the operations of addition and multiplication. To obtain a more accurate result, you can enter additional variables that take into account the errors. Say, add a variable that takes into account the error in the operation of accumulating the main error in the TwoSum () function. Then this error will have the order of EPSILON 2 , in relation to the main result (the first error will have the order of EPSILON ).
Multiplication rounding error
We calculate the number 1.0012 101 in the cycle, i.e. do the following:
#include <stdio.h> #include <math.h> int main() { float val = 1.0012; float result = 1.0012; for (long long i = 0; i < 100; i++) { result *= val; } printf("%0.15g \n", result); return 0; } Note that the exact result, up to the fifteenth decimal place, is 1.128768638496750. We will receive: 1.12876391410828. As you can see, the error was quite large.
Let's output the val variable, casting it to the double data type, and see what is actually written to it:
printf("%0.15g \n", (double)val); We get the number 1.00119996070862. This suggests that in programming, even the most accurate constant is neither reliable nor constant. Therefore, our real exact result will be 1.128764164435784, up to the fifteenth decimal place.
Now we will try to improve the result obtained earlier. To do this, we introduce compensation for the result of calculations, by taking into account the rounding error in the multiplication operation. We will also try to add the accumulated error to the result variable at each step.
Code:
#include <stdio.h> #include <math.h> float TwoSum(float a, float b, float& error, bool isNull) { //isNull , // float x = a + b; float b_virt = x - a; float a_virt = x - b_virt; float b_roundoff = b - b_virt; float a_roudnoff = a - a_virt; float y = a_roudnoff + b_roundoff; if (isNull) { error = y; } else { error += y; } return x; } void Split(float a, int s, float& a_hi, float& a_lo) { float c = (pow(2, s) + 1)*a; float a_big = c - a; a_hi = c - a_big; a_lo = a - a_hi; } float TwoProduct(float a, float b, float& err) { float x = a*b; float a_hi, a_low, b_hi, b_low; Split(a, 12, a_hi, a_low); Split(b, 12, b_hi, b_low); float err1, err2, err3; err1 = x - (a_hi*b_hi); err2 = err1 - (a_low*b_hi); err3 = err2 - (a_hi*b_low); err += ((a_low * b_low) - err3); return x; } int main() { float val = 1.0012; float result = 1.0012; float errorMain = 0.0; for (long long i = 0; i < 100; i++) { result = TwoProduct(result, val, errorMain); result = TwoSum(errorMain, result, errorMain, true); } printf("%0.15g \n", result); return 0; } The program displays the following number: 1.12876415252686. We got an error of 1.0e-008, which is less than EPSILON / 2 for the float data type . Thus, this result can be considered quite good.
Results
1) In this paper, the presentation of floating-point numbers in the format of IEEE 754-2008 standard was considered.
2) The method of finding rounding errors in the operations of addition and multiplication of floating point numbers was shown.
3) Simple examples of compensation for rounding errors in floating-point numbers were considered.
The work was performed by Victor Fadeev.
Advised Makarov A.The.
PS Thanks for the errors found by users:
xeioex , albom .
References
- Works Makarov Andrei Vladimirovich on the topic "Representation of real numbers." The makarov_float .pdf file shows how rounding errors occur in floating-point numbers.
- Wikipedia . Single precision number.
- Adaptive Precision Floating-Point Arithmetic
and Fast Robust Geometric Predicates
Jonathan richard shewchuk
Source: https://habr.com/ru/post/266023/
All Articles