Deliver voice to mobile network: step 2 - Analog Digital Conversion
In the first part of a series of articles, we looked at the conversion of the human voice into an electrical signal. Now, it would seem, it's time to transmit this signal to the location of the interlocutor and start a conversation! That is exactly what they did originally. However, the more popular the service became and the longer it was necessary to transmit a signal, the clearer it became that the analog signal was not suitable for this.
In order to ensure the transfer of information to any distance without loss of quality, we will need to perform a second conversion from Analog to Digital.
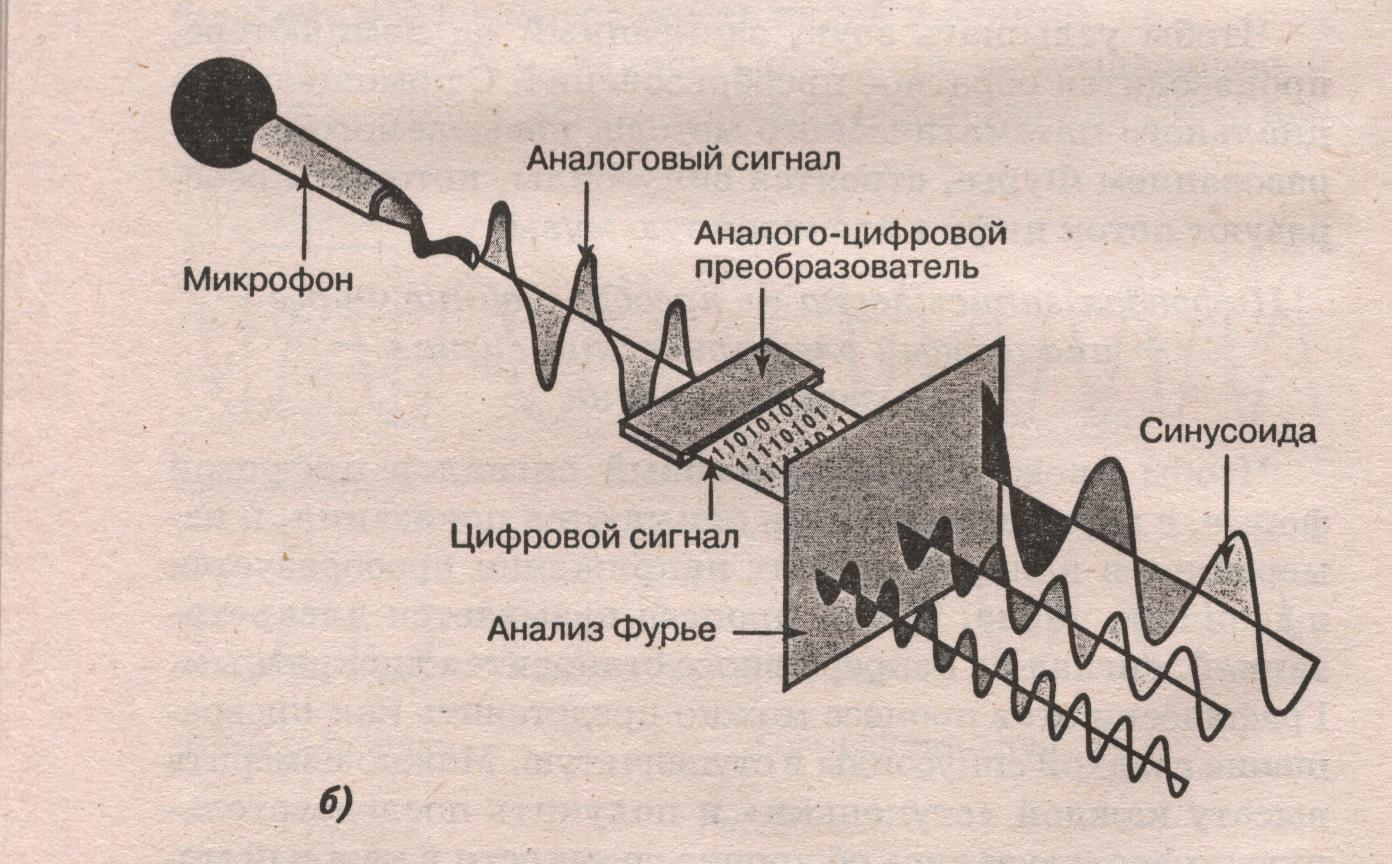
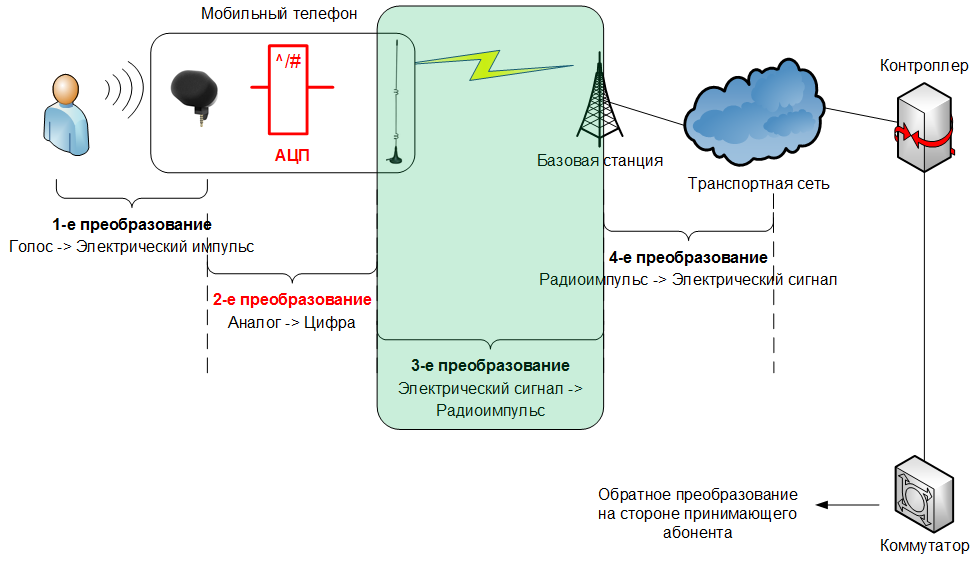
This picture gives the most visual idea of what happens during the Analog Digital Conversion (ADC), and then we look at why this is needed, how the technology has developed, and what requirements are imposed on such a transformation in mobile networks.
')
Those who missed or forgot, what was discussed in the first part, can remember How we received an electrical signal from sound vibrations , and we will continue the description of transformations by moving around the picture, which indicates a new area that interests us at the moment:
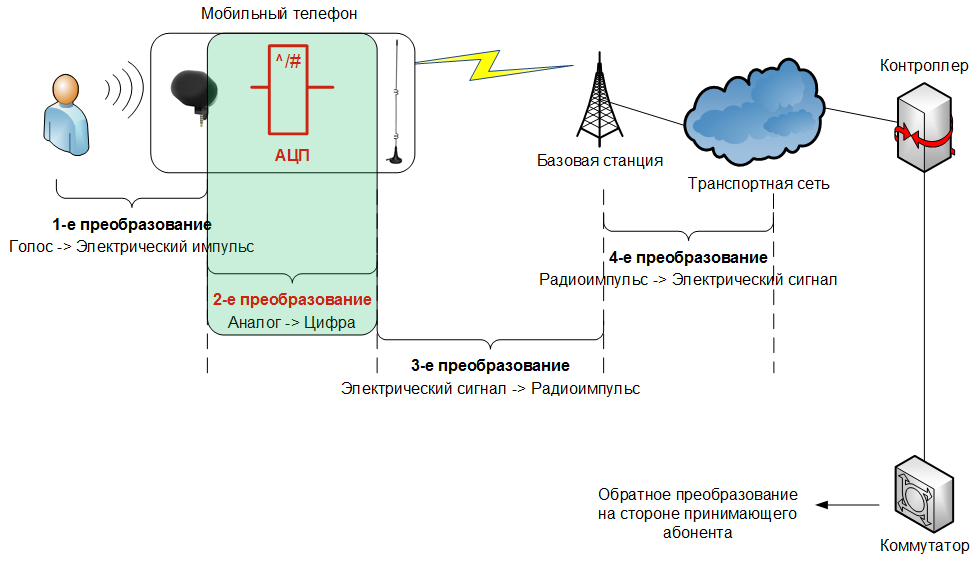
First, let's understand why it is generally necessary to convert an analog signal into some sequence of zeros and ones, which cannot be heard without special knowledge and mathematical transformations.
After the microphone, we have an analog electrical signal, which can be easily “voiced” using a speaker, which, in fact, was done in the first experiments with telephones: the inverse “electrical signal - sound wave” transformation was performed in the same room or at a minimum distance.
Just what is this phone for? In the next room you can bring sound information without any transformations - just by raising your voice. Therefore, the task appears - to hear the interlocutor at the maximum distance from the initiator of the conversation.
And here inexorable laws of nature come into force: the greater the distance, the stronger the electrical signal in the wires fades, and after a certain number of meters / kilometers it will be impossible to recover the sound from it.
Those who found fixed-line telephones working with decade-step PBXs (analog telephone exchanges) remember well what voice quality was sometimes provided with the help of these devices. And someone can remember such forgotten exotic inclusions “through a blocker” / “parallel telephone”, when two telephones in one house were switched on to one telephone line, while, when one subscriber occupied the line, the second one was forced to wait for the end of his conversation . Believe me - it was not easy!
That is, to increase the number of simultaneous calls between two points, using analog lines, we need to lay more and more wires. What this can lead to can be estimated from the urban landscapes of the beginning of the last century:


Therefore, immediately after the invention of the telephone, the best engineers set about solving the problem: how to transmit the voice over long distances with maximum quality preservation and minimal equipment costs.
What do we need in order for a continuous analog electric signal to become discrete, encoded with sequences of zeros and ones, and at the same time transmit information as close as possible to the original?
A bit of theory.
To convert any analog signal to digital, it is necessary at certain intervals (the sampling step in the picture below) to record the signal amplitude with a certain accuracy (quantization step).
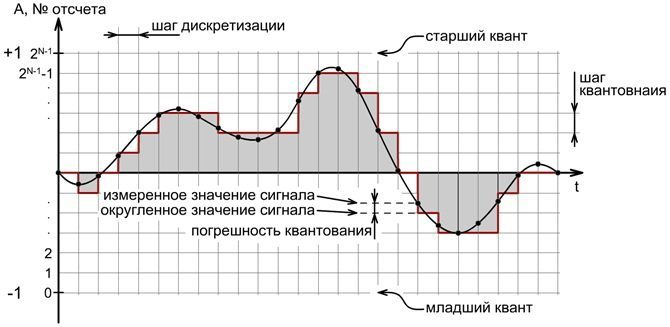
After digitizing, you will get a stepped graph shown in the figure. To get the digitized signal as close as possible to the analog one, the sampling step is necessary and the quantization step should be chosen as small as possible; for infinite values, we will get a perfectly digitized record.
In practice, infinite digitization accuracy is not required, and you need to choose what accuracy can be considered sufficient for voice transmission with the required quality?
Here we will come to the aid of knowledge about the sensitivity of human hearing organs: it is commonly assumed that a person can distinguish sounds with a frequency from 20 Hz to 22 000 Hz. These are the boundary values for discretization that will allow to transmit any sound perceived by a person. If we translate Hz into more familiar seconds, we get 0.000045 seconds, that is, measurements must be taken every 4.5 hundred thousandths of a second! Moreover, this is not enough. The reasons and the required values of the sampling rate will be described below.
Now we will determine the quantization step: the quantization step allows us to assign a certain amplitude value to the measured signal at each time instant.
In the first approximation, you can simply check the presence or absence of a signal, to describe such a number of options, we only need two values: 0 and 1. In computer science, this corresponds to the amount of information: 1 bit and the recording bit will be 1. If you digitize any sound with such bit depth , at the output we get a discontinuous recording, consisting of pauses and the sound of one tone, it can hardly be called a voice recording.
Therefore, it is necessary to increase the number of measured amplitude options, for example, to 4 (that is, up to 2 bits - 2 to the power of 2): 0 - 0.25 mA - 0.5 mA - 0.75 mA.
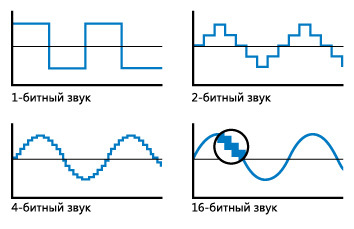
With such values, it will be possible to distinguish some changes in the sound after digitization, and not just its presence or absence. An illustration that perfectly shows what gives us an increase in bit depth (quantization) when digitizing sound is shown in this figure:
Now, having seen the numbers 44 kHz / 16 bits in the properties of the music file, you can immediately understand that the Analog-Digital Conversion was done with a sampling of 1 / 44kHz = 0.000023 seconds and with a quantization depth of 2 to 16 degrees - 65,536 value choices.
The first circuit solutions for performing ADC-DAC transformations were, as always, large and slow:

Now these tasks are performed in the main processor of the mobile phone, which simultaneously copes with a huge number of other tasks:

If you digitize without additional optimization of the obtained digital model, the amount of data received will be very large, it is enough to remember how much space on your disc an audio file can take in uncompressed form. A standard CD, for example, is 780 megabytes of information and only 74 minutes of sound!
After processing such a file using optimization algorithms and data loss compression (for example, mp3), the file size can be reduced 10 or more times.
For our purposes, the amount of data received is of fundamental importance, since it is still necessary to transmit them to your interlocutor, and the resource of the transport channel is very limited.
Again, the challenge for engineers is to maximize the amount of data transferred while maintaining the required quality.
In conversational speech, which sounds during a telephone dialogue, the frequency spectrum is significantly lower than that available for perception, therefore, to transmit a telephone conversation, you can limit yourself to a narrower spectrum: for example, 50..7000 Hz. We wrote about this in sufficient detail in the article on voice codecs in mobile networks.
Now we have the initial data for the start of the conversion - an electrical analog signal, in the range of 50-7000 Hz, and we need to carry out the A-CPU conversion so that the signal distortion during the conversion (those steps on the graph above) does not affect the recording quality . To do this, select the values of the sampling step and quantization step, sufficient for a complete description of the existing analog signal.
Here we come to the aid of one of the fundamental theorems in the field of digital signal processing - the Kotelnikov Theorem .
In it, our compatriot mathematically justified the frequency with which it is necessary to measure the values of a function for its exact numerical representation. For us, the most important consequence of this theorem is as follows: measurements should be carried out twice as often as the highest frequency, which we need to translate into a digital form.
Therefore, the discretization step for digitizing the conversation will be enough to take at the level of 14 kHz, and for high-quality digitization of music - 2 x 22 kHz, here we get the standard 44 kHz, with which now, as a rule, music files are created.
There are a large number of a wide variety of voice codecs that can be used in wired and wireless networks, with codecs for wired networks, in general, encode voice with better quality, and codecs for wireless networks (networks of mobile operators) with slightly worse quality.
But these codecs generate additional data to restore the received signal in case of unsuccessful delivery due to complex radio conditions. This feature is called noise immunity, and the development of codecs for mobile networks occurs in the direction of improving the quality of the transmitted signal while increasing its noise immunity.
Mobile networks use whole classes of voice codecs, which include a set of dynamically selectable encoding rates, depending on the current subscriber position and the quality of radio coverage at this point:
The table lists all codecs used in modern mobile networks, of which codecs with dynamic bitrate (in which the ratio of useful data and redundant data for data recovery changes) are called AMR - Adaptive Multi Rate. FR / HR / EFR codecs are used only in GSM networks.
To visualize how much more data is encoded in high-speed codecs, take a look at the following picture:
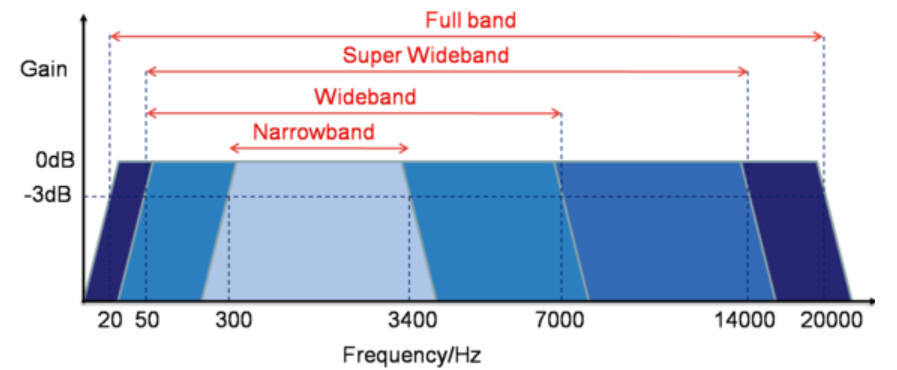
The transition from AMR codecs to AMR-WB almost doubles the amount of data, and AMR-WB + requires another 40-50% more than the width of the transport channel!
That is why in mobile networks, broadband codecs in mobile networks have not yet found wide application, but in the future it is possible to switch to the Super Wide Band (AMR-WB +) and even to the Full Band band, for example, for online broadcasts of concerts.
So - after performing the second stage of voice conversion, instead of sound vibrations, we receive a stream of digital data ready for transmission via the transport network.
Until the moment of the inverse conversion of numbers to an analog signal, this data remains almost unchanged (sometimes in the process of voice delivery transcoding from one codec to another may occur), and further transformations taking place with our voice will affect the physical medium through which the call is transmitted.
In the next article, we will look at what happens between the phone and the base station, and how miraculously the data stream that we form is delivered wirelessly to the operator’s equipment.
PS To everyone who is interested in the topic of digital communication and the history of its development, I highly recommend the book “And the Mysterious World behind the Curtain of Numbers” authors B.I. Kruk, G.N.Popov. From the point of view of modern standards and technologies, it is a bit outdated, but the authors describe the theoretical and historical part perfectly well, diluting the dry theory with living examples and illustrations.
In order to ensure the transfer of information to any distance without loss of quality, we will need to perform a second conversion from Analog to Digital.

This picture gives the most visual idea of what happens during the Analog Digital Conversion (ADC), and then we look at why this is needed, how the technology has developed, and what requirements are imposed on such a transformation in mobile networks.
')
Those who missed or forgot, what was discussed in the first part, can remember How we received an electrical signal from sound vibrations , and we will continue the description of transformations by moving around the picture, which indicates a new area that interests us at the moment:

First, let's understand why it is generally necessary to convert an analog signal into some sequence of zeros and ones, which cannot be heard without special knowledge and mathematical transformations.
After the microphone, we have an analog electrical signal, which can be easily “voiced” using a speaker, which, in fact, was done in the first experiments with telephones: the inverse “electrical signal - sound wave” transformation was performed in the same room or at a minimum distance.
Just what is this phone for? In the next room you can bring sound information without any transformations - just by raising your voice. Therefore, the task appears - to hear the interlocutor at the maximum distance from the initiator of the conversation.
And here inexorable laws of nature come into force: the greater the distance, the stronger the electrical signal in the wires fades, and after a certain number of meters / kilometers it will be impossible to recover the sound from it.
Those who found fixed-line telephones working with decade-step PBXs (analog telephone exchanges) remember well what voice quality was sometimes provided with the help of these devices. And someone can remember such forgotten exotic inclusions “through a blocker” / “parallel telephone”, when two telephones in one house were switched on to one telephone line, while, when one subscriber occupied the line, the second one was forced to wait for the end of his conversation . Believe me - it was not easy!
That is, to increase the number of simultaneous calls between two points, using analog lines, we need to lay more and more wires. What this can lead to can be estimated from the urban landscapes of the beginning of the last century:


Therefore, immediately after the invention of the telephone, the best engineers set about solving the problem: how to transmit the voice over long distances with maximum quality preservation and minimal equipment costs.
What do we need in order for a continuous analog electric signal to become discrete, encoded with sequences of zeros and ones, and at the same time transmit information as close as possible to the original?
A bit of theory.
To convert any analog signal to digital, it is necessary at certain intervals (the sampling step in the picture below) to record the signal amplitude with a certain accuracy (quantization step).

After digitizing, you will get a stepped graph shown in the figure. To get the digitized signal as close as possible to the analog one, the sampling step is necessary and the quantization step should be chosen as small as possible; for infinite values, we will get a perfectly digitized record.
In practice, infinite digitization accuracy is not required, and you need to choose what accuracy can be considered sufficient for voice transmission with the required quality?
Here we will come to the aid of knowledge about the sensitivity of human hearing organs: it is commonly assumed that a person can distinguish sounds with a frequency from 20 Hz to 22 000 Hz. These are the boundary values for discretization that will allow to transmit any sound perceived by a person. If we translate Hz into more familiar seconds, we get 0.000045 seconds, that is, measurements must be taken every 4.5 hundred thousandths of a second! Moreover, this is not enough. The reasons and the required values of the sampling rate will be described below.
Now we will determine the quantization step: the quantization step allows us to assign a certain amplitude value to the measured signal at each time instant.
In the first approximation, you can simply check the presence or absence of a signal, to describe such a number of options, we only need two values: 0 and 1. In computer science, this corresponds to the amount of information: 1 bit and the recording bit will be 1. If you digitize any sound with such bit depth , at the output we get a discontinuous recording, consisting of pauses and the sound of one tone, it can hardly be called a voice recording.
Therefore, it is necessary to increase the number of measured amplitude options, for example, to 4 (that is, up to 2 bits - 2 to the power of 2): 0 - 0.25 mA - 0.5 mA - 0.75 mA.
With such values, it will be possible to distinguish some changes in the sound after digitization, and not just its presence or absence. An illustration that perfectly shows what gives us an increase in bit depth (quantization) when digitizing sound is shown in this figure:

Now, having seen the numbers 44 kHz / 16 bits in the properties of the music file, you can immediately understand that the Analog-Digital Conversion was done with a sampling of 1 / 44kHz = 0.000023 seconds and with a quantization depth of 2 to 16 degrees - 65,536 value choices.
The first circuit solutions for performing ADC-DAC transformations were, as always, large and slow:

Now these tasks are performed in the main processor of the mobile phone, which simultaneously copes with a huge number of other tasks:

If you digitize without additional optimization of the obtained digital model, the amount of data received will be very large, it is enough to remember how much space on your disc an audio file can take in uncompressed form. A standard CD, for example, is 780 megabytes of information and only 74 minutes of sound!
After processing such a file using optimization algorithms and data loss compression (for example, mp3), the file size can be reduced 10 or more times.
For our purposes, the amount of data received is of fundamental importance, since it is still necessary to transmit them to your interlocutor, and the resource of the transport channel is very limited.
Again, the challenge for engineers is to maximize the amount of data transferred while maintaining the required quality.
In conversational speech, which sounds during a telephone dialogue, the frequency spectrum is significantly lower than that available for perception, therefore, to transmit a telephone conversation, you can limit yourself to a narrower spectrum: for example, 50..7000 Hz. We wrote about this in sufficient detail in the article on voice codecs in mobile networks.
Now we have the initial data for the start of the conversion - an electrical analog signal, in the range of 50-7000 Hz, and we need to carry out the A-CPU conversion so that the signal distortion during the conversion (those steps on the graph above) does not affect the recording quality . To do this, select the values of the sampling step and quantization step, sufficient for a complete description of the existing analog signal.
Here we come to the aid of one of the fundamental theorems in the field of digital signal processing - the Kotelnikov Theorem .
In it, our compatriot mathematically justified the frequency with which it is necessary to measure the values of a function for its exact numerical representation. For us, the most important consequence of this theorem is as follows: measurements should be carried out twice as often as the highest frequency, which we need to translate into a digital form.
Therefore, the discretization step for digitizing the conversation will be enough to take at the level of 14 kHz, and for high-quality digitization of music - 2 x 22 kHz, here we get the standard 44 kHz, with which now, as a rule, music files are created.
There are a large number of a wide variety of voice codecs that can be used in wired and wireless networks, with codecs for wired networks, in general, encode voice with better quality, and codecs for wireless networks (networks of mobile operators) with slightly worse quality.
But these codecs generate additional data to restore the received signal in case of unsuccessful delivery due to complex radio conditions. This feature is called noise immunity, and the development of codecs for mobile networks occurs in the direction of improving the quality of the transmitted signal while increasing its noise immunity.
Mobile networks use whole classes of voice codecs, which include a set of dynamically selectable encoding rates, depending on the current subscriber position and the quality of radio coverage at this point:
| Codec | Standard | Year of creation | Compressible frequency range | Generated bitrate |
|---|---|---|---|---|
| Full Rate - FR | GSM 06.10 | 1990 | 200-3400 Hz | FR 13 kbit / s |
| Half Rate - HR | GSM 06.20 | 1990 | 200-3400 Hz | HR 5.6 kbit / s |
| Enhanced Full Rate - EFR | GSM 06.60 | 1995 | 200-3400 Hz | FR 12.2 kbit / s |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR 12.20 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR 10.20 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR / HR 7.95 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR / HR 7.40 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR / HR 6.70 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR / HR 5.90 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR / HR 5.15 |
| Adaptive Multi Rate - AMR | 3GPP TS 26.071 | 1999 | 200-3400 Hz | FR / HR 4.75 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 23.85 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 23.05 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 19.85 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 18.25 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 15.85 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 14.25 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 12.65 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 8.85 |
| Adaptive Multi Rate - WideBand, AMR-WB | 3GPP TS 26.190 | 2001 | 50-7000 Hz | FR 6.60 |
| Adaptive Multi Rate-WideBand +, AMR-WB + | 3GPP TS 26.290 | 2004 | 50-7000 Hz | 6 - 36 kbit / s (mono) |
| Adaptive Multi Rate-WideBand +, AMR-WB + | 3GPP TS 26.290 | 2004 | 50-7000 Hz | 7 - 48 kbit / s (stereo) |
The table lists all codecs used in modern mobile networks, of which codecs with dynamic bitrate (in which the ratio of useful data and redundant data for data recovery changes) are called AMR - Adaptive Multi Rate. FR / HR / EFR codecs are used only in GSM networks.
To visualize how much more data is encoded in high-speed codecs, take a look at the following picture:

The transition from AMR codecs to AMR-WB almost doubles the amount of data, and AMR-WB + requires another 40-50% more than the width of the transport channel!
That is why in mobile networks, broadband codecs in mobile networks have not yet found wide application, but in the future it is possible to switch to the Super Wide Band (AMR-WB +) and even to the Full Band band, for example, for online broadcasts of concerts.
So - after performing the second stage of voice conversion, instead of sound vibrations, we receive a stream of digital data ready for transmission via the transport network.
Until the moment of the inverse conversion of numbers to an analog signal, this data remains almost unchanged (sometimes in the process of voice delivery transcoding from one codec to another may occur), and further transformations taking place with our voice will affect the physical medium through which the call is transmitted.
In the next article, we will look at what happens between the phone and the base station, and how miraculously the data stream that we form is delivered wirelessly to the operator’s equipment.

PS To everyone who is interested in the topic of digital communication and the history of its development, I highly recommend the book “And the Mysterious World behind the Curtain of Numbers” authors B.I. Kruk, G.N.Popov. From the point of view of modern standards and technologies, it is a bit outdated, but the authors describe the theoretical and historical part perfectly well, diluting the dry theory with living examples and illustrations.
Source: https://habr.com/ru/post/265841/
All Articles