Geekly Articles each Day
📜 ⬆️ ⬇️

Fourier processing of digital images

Foreword


A digital photograph or other raster image is an array of numbers recorded by the brightness levels sensors in a two-dimensional plane. Knowing that from a mathematical point of view, a thin lens performs the Fourier transform of images placed in focal planes, it is possible to create image processing algorithms that are analogous to image processing by a classical optical system.

The formula of such algorithms will be as follows:
  1. Z = FFT (X) is the direct two-dimensional Fourier transform
  2. Z ′ = T (Z) - application of the function or transparency to the Fourier transform of the image
  3. Y = BFT (Z) is the inverse two-dimensional Fourier transform

To calculate the Fourier transforms, the Fast Discrete Fourier Transform algorithms are used. Although the optical system of lenses performs the Fourier transform on the continuous range of the argument for the continuous spectrum, but when switching to digital data processing, the Fourier transform formulas can be replaced with the discrete Fourier transform formulas.

Implementation examples



The implemented algorithms are part of the open source FFTTools library. Internet address: github.com/dprotopopov/FFTTools

Image Blur Algorithm


In optical systems, the aperture located in the focal plane is a simple hole in the screen. As a result of the passage of the light flux through the diaphragm, the high-frequency waves (with shorter wavelengths) pass through an obstacle, and the low-frequency waves (with longer wavelengths) are cut off by the screen. This increases the sharpness of the resulting image. If you replace the hole in the screen with an obstacle in the screen, the result will be a blurred image, since it will be formed from the frequencies of waves of great lengths.
')
Algorithm:
  1. Let X (N1, N2) be the array of brightness of the image pixels.
  2. Calculate Px = the mean (root mean square) brightness of the pixels in the array X
  3. Calculate the array Z = FT (X) - direct two-dimensional discrete Fourier transform
  4. Calculate the array Z ′ = T (Z), where T is the zeroing of rows and columns located in the specified internal regions of the matrix argument corresponding to the high frequencies 5. (i.e., the zeroing of the Fourier expansion coefficients corresponding to high frequencies)
  5. Calculate the array Y = RFT (Z ′) - the inverse two-dimensional discrete Fourier transform
  6. Calculate Py = Mean (RMS) Brightness of Pixels in Array Y
  7. Normalize the array Y (N1, N2) on the average level of brightness Px / Py

Image Sharpening Algorithm


In optical systems, the aperture located in the focal plane is a simple hole in the screen. As a result of the passage of the light flux through the diaphragm, the high-frequency waves (with shorter wavelengths) pass through an obstacle, and the low-frequency waves (with longer wavelengths) are cut off by the screen. This increases the sharpness of the resulting image.

Algorithm:
  1. Let X (N1, N2) be the array of brightness of the image pixels.
  2. Calculate Px = the mean (root mean square) brightness of the pixels in the array X
  3. Calculate the array Z = FT (X) - direct two-dimensional discrete Fourier transform
  4. Save value L = Z (0,0) - corresponding to the average brightness of the pixels of the original image
  5. Calculate the array Z ′ = T (Z), where T is the zeroing of rows and columns located in the specified external regions of the matrix argument corresponding to the low 6. frequencies (i.e. zeroing of the Fourier expansion coefficients corresponding to low frequencies)
  6. Restore Z 'value (0,0) = L - corresponding to the average brightness of the pixels of the original image
  7. Calculate the array Y = RFT (Z ′) - the inverse two-dimensional discrete Fourier transform
  8. Calculate Py = Mean (RMS) Brightness of Pixels in Array Y
  9. Normalize the array Y (N1, N2) on the average level of brightness Px / Py

Image scaling algorithm


In optical systems, the light flux in the focal plane of the system is the Fourier transform of the original image. The size of the image obtained at the output of the optical system is determined by the ratio of the focal distances of the lens and the eyepiece.

Algorithm:
  1. Let X (N1, N2) be the array of brightness of the image pixels.
  2. Calculate Px = the mean (root mean square) brightness of the pixels in the array X
  3. Calculate the array Z = FT (X) - direct two-dimensional discrete Fourier transform
  4. Calculate the array Z ′ = T (Z), where T is either adding zero rows and matrix columns corresponding to high frequencies, or removing matrix rows and columns corresponding to high frequencies to obtain the required size of the final image
  5. Calculate the array Y = RFT (Z ′) - the inverse two-dimensional discrete Fourier transform
  6. Calculate Py = Mean (RMS) Brightness of Pixels in Array Y
  7. Normalize the array Y (M1, M2) at the average level of brightness Px / Py

Used software

Image Blur Algorithm


Algorithm Code
/// <summary> /// Clear internal region of array /// </summary> /// <param name="data">Array of values</param> /// <param name="size">Internal blind region size</param> private static void Blind(Complex[,,] data, Size size) { int n0 = data.GetLength(0); int n1 = data.GetLength(1); int n2 = data.GetLength(2); int s0 = Math.Max(0, (n0 - size.Height)/2); int s1 = Math.Max(0, (n1 - size.Width)/2); int e0 = Math.Min((n0 + size.Height)/2, n0); int e1 = Math.Min((n1 + size.Width)/2, n1); for (int i = s0; i < e0; i++) { Array.Clear(data, i*n1*n2, n1*n2); } for (int i = 0; i < s0; i++) { Array.Clear(data, i*n1*n2 + s1*n2, (e1 - s1)*n2); } for (int i = e0; i < n0; i++) { Array.Clear(data, i*n1*n2 + s1*n2, (e1 - s1)*n2); } } /// <summary> /// Blur bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Blured bitmap</returns> public Bitmap Blur(Bitmap bitmap) { using (var image = new Image<Bgr, double>(bitmap)) { int length = image.Data.Length; int n0 = image.Data.GetLength(0); int n1 = image.Data.GetLength(1); int n2 = image.Data.GetLength(2); var doubles = new double[length]; Buffer.BlockCopy(image.Data, 0, doubles, 0, length*sizeof (double)); double power = Math.Sqrt(doubles.Average(x => x*x)); var input = new fftw_complexarray(doubles.Select(x => new Complex(x, 0)).ToArray()); var output = new fftw_complexarray(length); fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Forward, fftw_flags.Estimate).Execute(); Complex[] complex = output.GetData_Complex(); var data = new Complex[n0, n1, n2]; var buffer = new double[length*2]; GCHandle complexHandle = GCHandle.Alloc(complex, GCHandleType.Pinned); GCHandle dataHandle = GCHandle.Alloc(data, GCHandleType.Pinned); IntPtr complexPtr = complexHandle.AddrOfPinnedObject(); IntPtr dataPtr = dataHandle.AddrOfPinnedObject(); Marshal.Copy(complexPtr, buffer, 0, buffer.Length); Marshal.Copy(buffer, 0, dataPtr, buffer.Length); Blind(data, _blinderSize); Marshal.Copy(dataPtr, buffer, 0, buffer.Length); Marshal.Copy(buffer, 0, complexPtr, buffer.Length); complexHandle.Free(); dataHandle.Free(); input.SetData(complex); fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Backward, fftw_flags.Estimate).Execute(); double[] array2 = output.GetData_Complex().Select(x => x.Magnitude).ToArray(); double power2 = Math.Sqrt(array2.Average(x => x*x)); doubles = array2.Select(x => x*power/power2).ToArray(); Buffer.BlockCopy(doubles, 0, image.Data, 0, length*sizeof (double)); return image.Bitmap; } }


Image Sharpening Algorithm


Algorithm Code
  /// <summary> /// Clear external region of array /// </summary> /// <param name="data">Array of values</param> /// <param name="size">External blind region size</param> private static void Blind(Complex[,,] data, Size size) { int n0 = data.GetLength(0); int n1 = data.GetLength(1); int n2 = data.GetLength(2); int s0 = Math.Max(0, (n0 - size.Height)/2); int s1 = Math.Max(0, (n1 - size.Width)/2); int e0 = Math.Min((n0 + size.Height)/2, n0); int e1 = Math.Min((n1 + size.Width)/2, n1); for (int i = 0; i < s0; i++) { Array.Clear(data, i*n1*n2, s1*n2); Array.Clear(data, i*n1*n2 + e1*n2, (n1 - e1)*n2); } for (int i = e0; i < n0; i++) { Array.Clear(data, i*n1*n2, s1*n2); Array.Clear(data, i*n1*n2 + e1*n2, (n1 - e1)*n2); } } /// <summary> /// Sharp bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Sharped bitmap</returns> public Bitmap Sharp(Bitmap bitmap) { using (var image = new Image<Bgr, double>(bitmap)) { int length = image.Data.Length; int n0 = image.Data.GetLength(0); int n1 = image.Data.GetLength(1); int n2 = image.Data.GetLength(2); var doubles = new double[length]; Buffer.BlockCopy(image.Data, 0, doubles, 0, length*sizeof (double)); double power = Math.Sqrt(doubles.Average(x => x*x)); var input = new fftw_complexarray(doubles.Select(x => new Complex(x, 0)).ToArray()); var output = new fftw_complexarray(length); fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Forward, fftw_flags.Estimate).Execute(); Complex[] complex = output.GetData_Complex(); Complex level = complex[0]; var data = new Complex[n0, n1, n2]; var buffer = new double[length*2]; GCHandle complexHandle = GCHandle.Alloc(complex, GCHandleType.Pinned); GCHandle dataHandle = GCHandle.Alloc(data, GCHandleType.Pinned); IntPtr complexPtr = complexHandle.AddrOfPinnedObject(); IntPtr dataPtr = dataHandle.AddrOfPinnedObject(); Marshal.Copy(complexPtr, buffer, 0, buffer.Length); Marshal.Copy(buffer, 0, dataPtr, buffer.Length); Blind(data, _blinderSize); Marshal.Copy(dataPtr, buffer, 0, buffer.Length); Marshal.Copy(buffer, 0, complexPtr, buffer.Length); complexHandle.Free(); dataHandle.Free(); complex[0] = level; input.SetData(complex); fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Backward, fftw_flags.Estimate).Execute(); double[] array2 = output.GetData_Complex().Select(x => x.Magnitude).ToArray(); double power2 = Math.Sqrt(array2.Average(x => x*x)); doubles = array2.Select(x => x*power/power2).ToArray(); Buffer.BlockCopy(doubles, 0, image.Data, 0, length*sizeof (double)); return image.Bitmap; } }


Image scaling algorithm


Algorithm Code
  /// <summary> /// Copy arrays /// </summary> /// <param name="input">Input array</param> /// <param name="output">Output array</param> private static void Copy(Complex[,,] input, Complex[,,] output) { int n0 = input.GetLength(0); int n1 = input.GetLength(1); int n2 = input.GetLength(2); int m0 = output.GetLength(0); int m1 = output.GetLength(1); int m2 = output.GetLength(2); int ex0 = Math.Min(n0, m0)/2; int ex1 = Math.Min(n1, m1)/2; int ex2 = Math.Min(n2, m2); Debug.Assert(n2 == m2); for (int k = 0; k < ex2; k++) { for (int i = 0; i <= ex0; i++) { for (int j = 0; j <= ex1; j++) { int ni = n0 - i - 1; int nj = n1 - j - 1; int mi = m0 - i - 1; int mj = m1 - j - 1; output[i, j, k] = input[i, j, k]; output[mi, j, k] = input[ni, j, k]; output[i, mj, k] = input[i, nj, k]; output[mi, mj, k] = input[ni, nj, k]; } } } } /// <summary> /// Resize bitmap with the Fastest Fourier Transform /// </summary> /// <returns>Resized bitmap</returns> public Bitmap Stretch(Bitmap bitmap) { using (var image = new Image<Bgr, double>(bitmap)) { int length = image.Data.Length; int n0 = image.Data.GetLength(0); int n1 = image.Data.GetLength(1); int n2 = image.Data.GetLength(2); var doubles = new double[length]; Buffer.BlockCopy(image.Data, 0, doubles, 0, length*sizeof (double)); double power = Math.Sqrt(doubles.Average(x => x*x)); var input = new fftw_complexarray(doubles.Select(x => new Complex(x, 0)).ToArray()); var output = new fftw_complexarray(length); fftw_plan.dft_3d(n0, n1, n2, input, output, fftw_direction.Forward, fftw_flags.Estimate).Execute(); Complex[] complex = output.GetData_Complex(); using (var image2 = new Image<Bgr, double>(_newSize)) { int length2 = image2.Data.Length; int m0 = image2.Data.GetLength(0); int m1 = image2.Data.GetLength(1); int m2 = image2.Data.GetLength(2); var complex2 = new Complex[length2]; var data = new Complex[n0, n1, n2]; var data2 = new Complex[m0, m1, m2]; var buffer = new double[length*2]; GCHandle complexHandle = GCHandle.Alloc(complex, GCHandleType.Pinned); GCHandle dataHandle = GCHandle.Alloc(data, GCHandleType.Pinned); IntPtr complexPtr = complexHandle.AddrOfPinnedObject(); IntPtr dataPtr = dataHandle.AddrOfPinnedObject(); Marshal.Copy(complexPtr, buffer, 0, buffer.Length); Marshal.Copy(buffer, 0, dataPtr, buffer.Length); complexHandle.Free(); dataHandle.Free(); Copy(data, data2); buffer = new double[length2*2]; complexHandle = GCHandle.Alloc(complex2, GCHandleType.Pinned); dataHandle = GCHandle.Alloc(data2, GCHandleType.Pinned); complexPtr = complexHandle.AddrOfPinnedObject(); dataPtr = dataHandle.AddrOfPinnedObject(); Marshal.Copy(dataPtr, buffer, 0, buffer.Length); Marshal.Copy(buffer, 0, complexPtr, buffer.Length); complexHandle.Free(); dataHandle.Free(); var input2 = new fftw_complexarray(complex2); var output2 = new fftw_complexarray(length2); fftw_plan.dft_3d(m0, m1, m2, input2, output2, fftw_direction.Backward, fftw_flags.Estimate).Execute(); double[] array2 = output2.GetData_Complex().Select(x => x.Magnitude).ToArray(); double power2 = Math.Sqrt(array2.Average(x => x*x)); double[] doubles2 = array2.Select(x => x*power/power2).ToArray(); Buffer.BlockCopy(doubles2, 0, image2.Data, 0, length2*sizeof (double)); return image2.Bitmap; } } }



Screenshots of programs


Blur image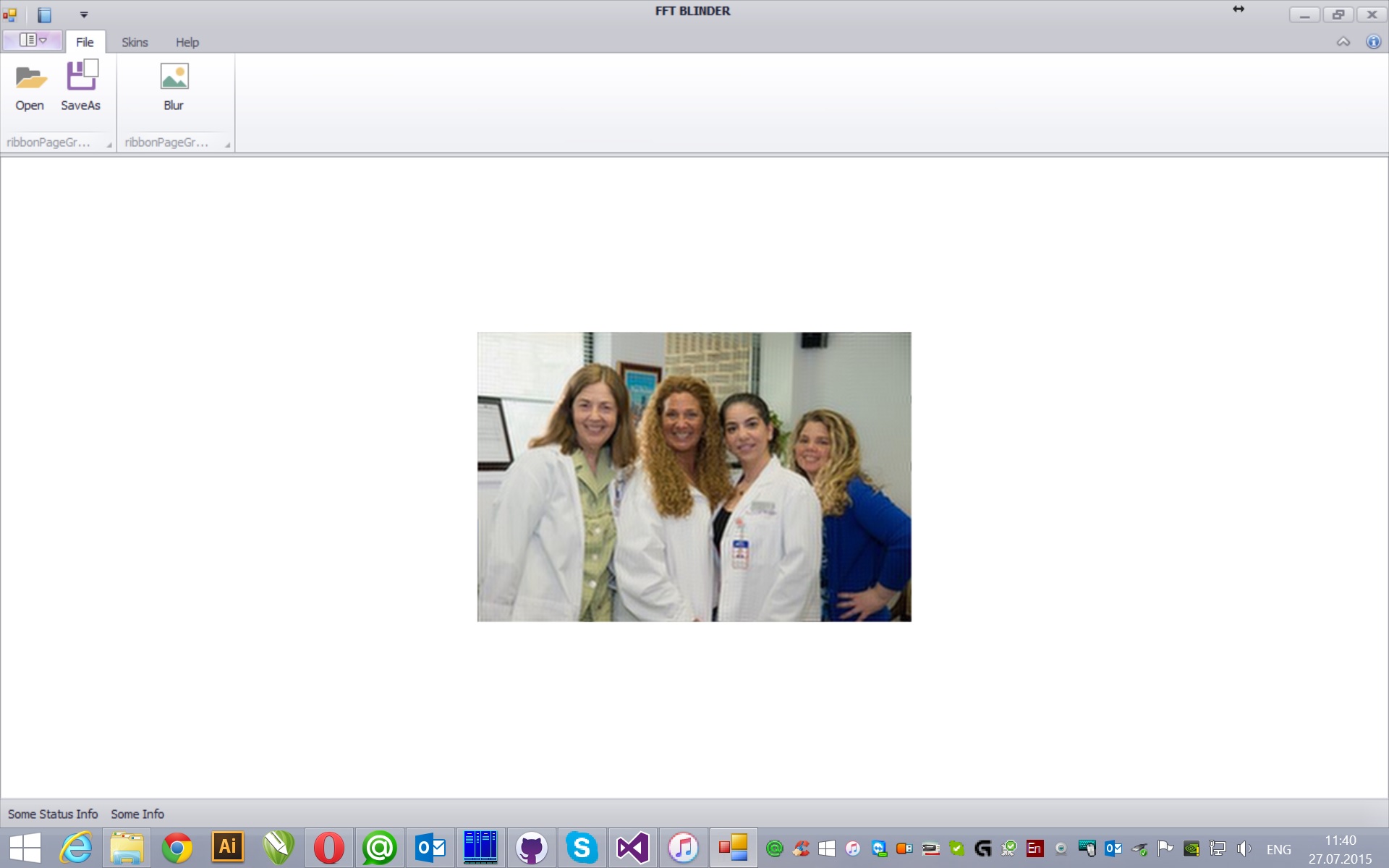
image


Image scaling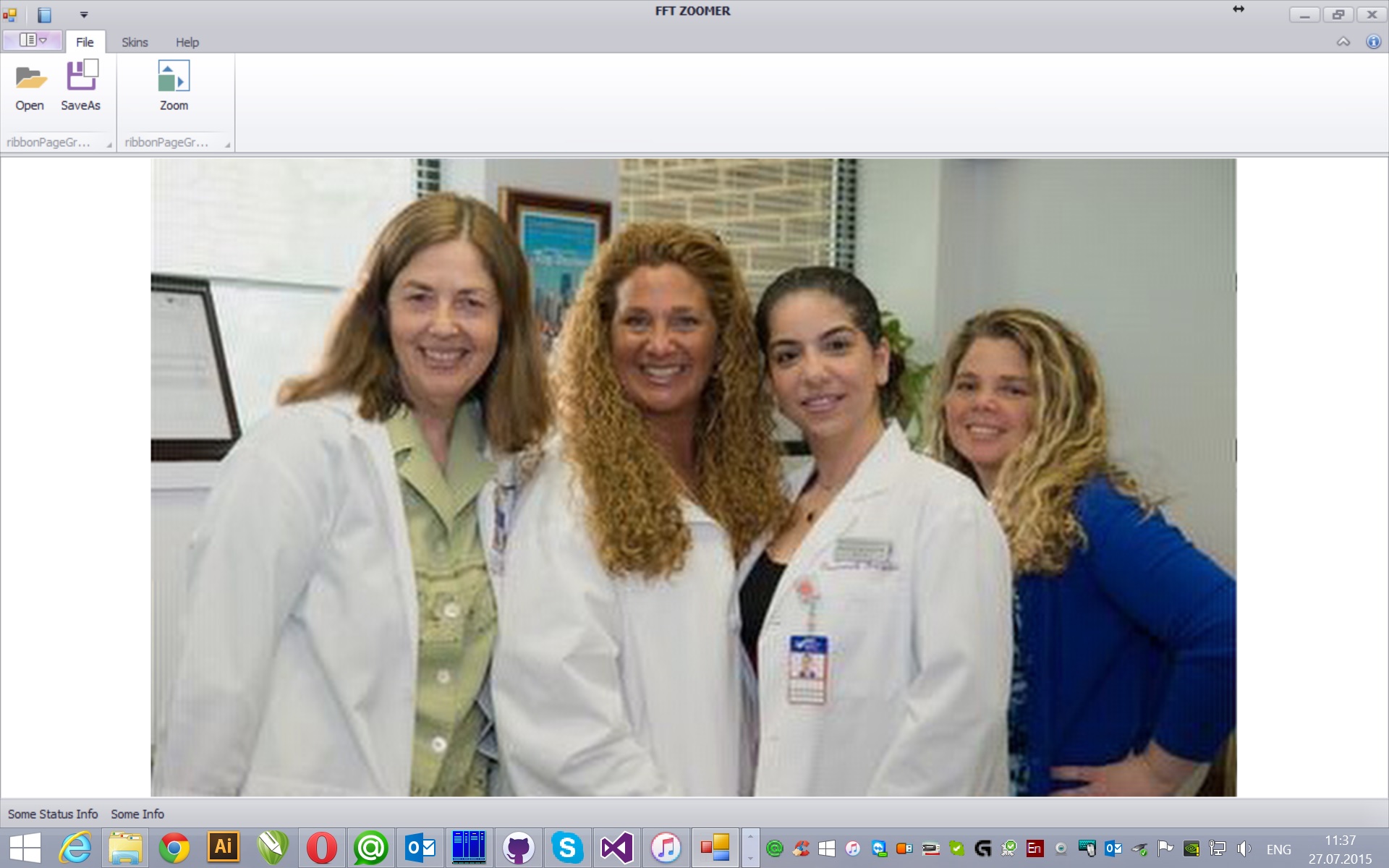
image


Literature


  1. A.L. Dmitriev. Optical methods of information processing. Tutorial. SPb. SPUGUITMO 2005. 46 p.
  2. A.A. Akaev, S..Mayorov “Optical methods of information processing” M.: 1988
  3. J. Goodman "Introduction to Fourier Optics" M .: Mir 1970

Source: https://habr.com/ru/post/265781/

More articles:


All Articles