We write the real noise of Perlin
According to the search query, the noise of the pearl immediately comes across this transfer to Habré. As rightly noted in the comments to the publication, this is not at all the noise of Perlin. Perhaps the author of the translation himself was not in the know.
What is the difference between the noise of Perlin, you caneasily notice if you compare the pictures.
Normal noise (from the same article):

')
Perlin's noise:

And by increasing the number of octaves, you can’t bring the first picture to the second. I will not describe the advantages of Perlin noise and its area of application (because the article is about programming, and not about application), but I will try to explain how it is implemented. I think this will be useful to many programmers, because the hacker sources of Ken Perlin do not explain much, even with comments.
Amazingly, judging by the reviews in PM and in the comments, it turned out that not everyone is able to see any difference at all between the simple smoothed noise in the grayscale and the Perlin noise. But, probably, because of this paradox, the very article appeared and raped.
I'll try to give a tip:
The first picture consists of distinct pixels (enlarged) in different shades of gray:

The second one (Perlin noise) looks like black and white blurry worms.
Here is what happens after simple operations in the graphical editor (search for boundaries, inversion, posterization):
Perlin:

Picture from the article (exactly the same operations are applied):

Yes, in fractal noise, if there are a lot of octaves, then it’s hard to understand what’s in the original - Perlin or not. But this is not a reason to call fractal noise Perlin noise.
On it I will finish with the description of a difference.
The end of the retreat.
Consider the two-dimensional option. For the time being, we will only write a blank class. The incoming data is a two-dimensional vector or two floating-point numbers: x, y.
The return value is a number from -1.0 to 1.0:
The idea of the usual smoothed noise is that there is a discrete pseudo-random grid of values, and for the requested point there is an interpolation between the grid nodes (the closer the point is to some grid node, the more its value corresponds to the node value).
Here in the third conventional square, the point in the very center after interpolation will have the value 3:
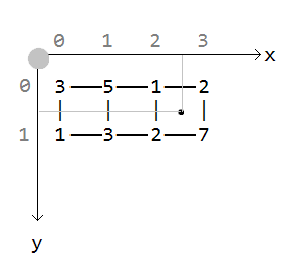
Consider in more detail how it turns out the three. Point coordinates:
The integer coordinates of the point (the upper left corner of the square):
are obtained by rounding down (floor function).
The local coordinates of a point inside a square are obtained by subtracting:
Take the value of the upper left corner of the square (1) and the upper right (2). Interpolate the top edge using the local x coordinate (0.5). Linear interpolation looks like this:
Take the value of the lower left corner of the square (2) and lower right (7). Interpolate the lower bound using the same local x coordinate (0.5).
Results:
Now there is an interpolation of the upper and lower using the local y coordinate (also 0.5):
Bilinear interpolation is the easiest but the result is not the most attractive.
Other interpolation options involve modifying the local coordinate (parameter t) before interpolation. Smoother transitions near the boundary values (0 and 1) are obtained.

The first variant is involved in Perlin’s noise; it gives a rather strong curvature.
Everything is very simple:
1. At the grid nodes, pseudo-random vectors (two-dimensional for two-dimensional noise, three-dimensional for three-dimensional, and so on), and not pseudo-random numbers .
2. Interpolate between the scalar products a) vectors from the vertices of a square to a point inside the square (a three-dimensional cube) and b) pseudo-random vectors (when describing Perlin noise, they are called gradient vectors).
In his improved version of the noise Ken Perlin uses a total of 12 gradient vectors. For the two-dimensional version, only 4 are required - by the number of faces (there are 4 in a square). The vectors are directed (conditionally from the center of the cube / square) towards each of the faces and are not normalized.
Here they are:

So, each of the grid nodes corresponds to one of the four vectors. Let the vector be an array of floats.
We need the scalar product of vectors:
Main method:
As a bonus:
And the last - use of the table with random numbers. In the Ken Pearl code, such a table is registered manually and the values obtained from there are quite different. Here you can experiment and the uniformity of noise and the absence of obvious patterns in it depend on this.
I did
Result:

What is the difference between the noise of Perlin, you can
Normal noise (from the same article):

')
Perlin's noise:

And by increasing the number of octaves, you can’t bring the first picture to the second. I will not describe the advantages of Perlin noise and its area of application (because the article is about programming, and not about application), but I will try to explain how it is implemented. I think this will be useful to many programmers, because the hacker sources of Ken Perlin do not explain much, even with comments.
Retreat
Amazingly, judging by the reviews in PM and in the comments, it turned out that not everyone is able to see any difference at all between the simple smoothed noise in the grayscale and the Perlin noise. But, probably, because of this paradox, the very article appeared and raped.
I'll try to give a tip:
The first picture consists of distinct pixels (enlarged) in different shades of gray:

The second one (Perlin noise) looks like black and white blurry worms.
Here is what happens after simple operations in the graphical editor (search for boundaries, inversion, posterization):
Perlin:

Picture from the article (exactly the same operations are applied):

Yes, in fractal noise, if there are a lot of octaves, then it’s hard to understand what’s in the original - Perlin or not. But this is not a reason to call fractal noise Perlin noise.
On it I will finish with the description of a difference.
The end of the retreat.
Consider the two-dimensional option. For the time being, we will only write a blank class. The incoming data is a two-dimensional vector or two floating-point numbers: x, y.
The return value is a number from -1.0 to 1.0:
public class Perlin2d { public float Noise(float x, float y) { throw new NotImplementedException(); } } Couple of words about interpolation
The idea of the usual smoothed noise is that there is a discrete pseudo-random grid of values, and for the requested point there is an interpolation between the grid nodes (the closer the point is to some grid node, the more its value corresponds to the node value).
Here in the third conventional square, the point in the very center after interpolation will have the value 3:

Consider in more detail how it turns out the three. Point coordinates:
x:2.5,
y:0.5
The integer coordinates of the point (the upper left corner of the square):
x:2,
y:0
are obtained by rounding down (floor function).
The local coordinates of a point inside a square are obtained by subtracting:
x = 2.5 – 2 = 0.5,
y = 0.5 – 0 = 0.5
Take the value of the upper left corner of the square (1) and the upper right (2). Interpolate the top edge using the local x coordinate (0.5). Linear interpolation looks like this:
static float Lerp(float a, float b, float t) { // return a * (t - 1) + b * t; ( , ): return a + (b - a) * t; } Take the value of the lower left corner of the square (2) and lower right (7). Interpolate the lower bound using the same local x coordinate (0.5).
Results:
: 1.5
: 4.5
Now there is an interpolation of the upper and lower using the local y coordinate (also 0.5):
1.5 * 0.5 + 4.5 * (1 – 0.5) = 3
Bilinear interpolation is the easiest but the result is not the most attractive.
Other interpolation options involve modifying the local coordinate (parameter t) before interpolation. Smoother transitions near the boundary values (0 and 1) are obtained.

The first variant is involved in Perlin’s noise; it gives a rather strong curvature.
static float QunticCurve(float t) { return t * t * t * (t * (t * 6 - 15) + 10); } ... // : Lerp(a, b, QuinticCurve(t)) The main idea and difference noise Perlin
Everything is very simple:
1. At the grid nodes, pseudo-random vectors (two-dimensional for two-dimensional noise, three-dimensional for three-dimensional, and so on), and not pseudo-random numbers .
2. Interpolate between the scalar products a) vectors from the vertices of a square to a point inside the square (a three-dimensional cube) and b) pseudo-random vectors (when describing Perlin noise, they are called gradient vectors).
In his improved version of the noise Ken Perlin uses a total of 12 gradient vectors. For the two-dimensional version, only 4 are required - by the number of faces (there are 4 in a square). The vectors are directed (conditionally from the center of the cube / square) towards each of the faces and are not normalized.
Here they are:
{ 1, 0 } { -1, 0 } { 0, 1 } { 0,-1 } 
So, each of the grid nodes corresponds to one of the four vectors. Let the vector be an array of floats.
float[] GetPseudoRandomGradientVector(int x, int y) { int v = // - 0 3 x y switch (v) { case 0: return new float[]{ 1, 0 }; case 1: return new float[]{ -1, 0 }; case 2: return new float[]{ 0, 1 }; default: return new float[]{ 0,-1 }; } } Implementation
We need the scalar product of vectors:
static float Dot(float[] a, float[] b) { return a[0] * b[0] + a[1] * b[1]; } Main method:
public float Noise(float fx, float fy) { // int left = (int)System.Math.Floor(fx); int top = (int)System.Math.Floor(fy); // float pointInQuadX = fx - left; float pointInQuadY = fy - top; // : float[] topLeftGradient = GetPseudoRandomGradientVector(left, top ); float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top ); float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1); float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1); // : float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY }; float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY }; float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 }; float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 }; // /* tx1--tx2 | | bx1--bx2 */ float tx1 = Dot(distanceToTopLeft, topLeftGradient); float tx2 = Dot(distanceToTopRight, topRightGradient); float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient); float bx2 = Dot(distanceToBottomRight, bottomRightGradient); // , : pointInQuadX = QunticCurve(pointInQuadX); pointInQuadY = QunticCurve(pointInQuadY); // , : float tx = Lerp(tx1, tx2, pointInQuadX); float bx = Lerp(bx1, bx2, pointInQuadX); float tb = Lerp(tx, bx, pointInQuadY); // : return tb; } As a bonus:
multi octave noise
public float Noise(float fx, float fy, int octaves, float persistence = 0.5f) { float amplitude = 1; // , "" // - persistence float max = 0; // float result = 0; // while (octaves-- > 0) { max += amplitude; result += Noise(fx, fy) * amplitude; amplitude *= persistence; fx *= 2; // ( ) fy *= 2; } return result/max; } And the last - use of the table with random numbers. In the Ken Pearl code, such a table is registered manually and the values obtained from there are quite different. Here you can experiment and the uniformity of noise and the absence of obvious patterns in it depend on this.
I did
So
& 3 here cuts off any int32 number to 3, read about AND operation on wikipedia
An operation like % 3 would also work, but much slower.
class Perlin2D { byte[] permutationTable; public Perlin2D(int seed = 0) { var rand = new System.Random(seed); permutationTable = new byte[1024]; rand.NextBytes(permutationTable); // } private float[] GetPseudoRandomGradientVector(int x, int y) { // - , int v = (int)(((x * 1836311903) ^ (y * 2971215073) + 4807526976) & 1023); v = permutationTable[v]&3; switch (v) { ... & 3 here cuts off any int32 number to 3, read about AND operation on wikipedia
An operation like % 3 would also work, but much slower.
The entire source code (no comments)
class Perlin2D { byte[] permutationTable; public Perlin2D(int seed = 0) { var rand = new System.Random(seed); permutationTable = new byte[1024]; rand.NextBytes(permutationTable); } private float[] GetPseudoRandomGradientVector(int x, int y) { int v = (int)(((x * 1836311903) ^ (y * 2971215073) + 4807526976) & 1023); v = permutationTable[v]&3; switch (v) { case 0: return new float[]{ 1, 0 }; case 1: return new float[]{ -1, 0 }; case 2: return new float[]{ 0, 1 }; default: return new float[]{ 0,-1 }; } } static float QunticCurve(float t) { return t * t * t * (t * (t * 6 - 15) + 10); } static float Lerp(float a, float b, float t) { return a + (b - a) * t; } static float Dot(float[] a, float[] b) { return a[0] * b[0] + a[1] * b[1]; } public float Noise(float fx, float fy) { int left = (int)System.Math.Floor(fx); int top = (int)System.Math.Floor(fy); float pointInQuadX = fx - left; float pointInQuadY = fy - top; float[] topLeftGradient = GetPseudoRandomGradientVector(left, top ); float[] topRightGradient = GetPseudoRandomGradientVector(left+1, top ); float[] bottomLeftGradient = GetPseudoRandomGradientVector(left, top+1); float[] bottomRightGradient = GetPseudoRandomGradientVector(left+1, top+1); float[] distanceToTopLeft = new float[]{ pointInQuadX, pointInQuadY }; float[] distanceToTopRight = new float[]{ pointInQuadX-1, pointInQuadY }; float[] distanceToBottomLeft = new float[]{ pointInQuadX, pointInQuadY-1 }; float[] distanceToBottomRight = new float[]{ pointInQuadX-1, pointInQuadY-1 }; float tx1 = Dot(distanceToTopLeft, topLeftGradient); float tx2 = Dot(distanceToTopRight, topRightGradient); float bx1 = Dot(distanceToBottomLeft, bottomLeftGradient); float bx2 = Dot(distanceToBottomRight, bottomRightGradient); pointInQuadX = QunticCurve(pointInQuadX); pointInQuadY = QunticCurve(pointInQuadY); float tx = Lerp(tx1, tx2, pointInQuadX); float bx = Lerp(bx1, bx2, pointInQuadX); float tb = Lerp(tx, bx, pointInQuadY); return tb; } public float Noise(float fx, float fy, int octaves, float persistence = 0.5f) { float amplitude = 1; float max = 0; float result = 0; while (octaves-- > 0) { max += amplitude; result += Noise(fx, fy) * amplitude; amplitude *= persistence; fx *= 2; fy *= 2; } return result/max; } } Result:

Source: https://habr.com/ru/post/265775/
All Articles