Intervals in C ++, part 4: to infinity and beyond
In the last part, I talked about the concept of incremental (Iterable) and showed how they solve many problems inherent in standard intervals. Now I will expand this concept to make infinite interval programming more secure and efficient.
Disclaimer : ideas in this post are more speculative than in previous ones. I will be glad to discuss .
In addition to the solved problems, which I mentioned in previous posts, there are still two. It:
iota_range is an infinite interval of integers, starting with some value and lasting forever. This is a sorted direct interval. Here are the algorithms of binary search, working with sorted direct intervals, will not work with him. It is impossible to conquer infinity by dividing (a good phrase turned out)
')
Is it possible to fix the STL algorithms so that they do not break when receiving an infinite interval? In their current form, no - it is impossible at the compilation stage to transmit information that any of the iterators denotes an infinite interval. Think about this: the following code will work:
but this will work "forever":
If rng.begin () has the same type as rng.end (), the two calls return the same instance of lower_bound. The function will not be able to determine whether it will work forever or not. But if it is possible to allow the signal iterator to be of a different type, we will be able to carry out this check at the compilation stage.
Suppose we have a type function (metafunction) called DenotesInfiniteSequence, which takes a pair of types (BeginType, EndType) and tells whether the sequence will be infinite. We have already determined that if BeginType and EndType are the same, then the DenotesInfiniteSequence should return false, since it will not be able to verify this in any way. But if they are different - for example, EndType will be of type unreachable_sentinel or something like that, then we will know at the compilation stage that the sequence is infinite.
Some intervals, by definition, will be infinite, even having an initial and final iterator of the same type.
I would like to immediately catch such errors, but, obviously, the binary function DenotesInfiniteSequence cannot cope with this. For zeros, the BeginType and EndType types will be the same, so the DenotesInfiniteSequence will return false.
Therefore, it is necessary to construct a unary function of the IsInfinite types that takes an interval type.
It can be used to define the concept of FiniteIterable.
Each FiniteIterable is iterable. There is a parallel hierarchy of refinements:
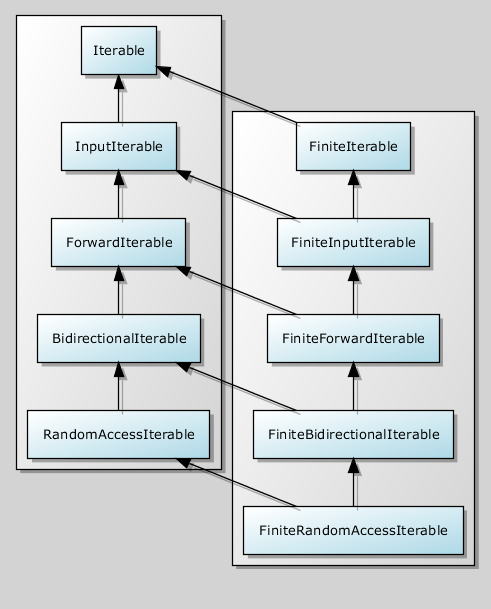
And all these concepts, by analogy with Range, do not need to be defined in the code. The finiteness is orthogonal to the Iterable hierarchy, and it can be queried separately.
But why FiniteIterable, and not InfiniteIterable? It's all about the algorithms and their requirements. There are no algorithms that require their interval arguments to be infinite. Therefore, it would be useless to be able to write InfiniteIterable. But an algorithm like lower_bound would like the interval to be finite. From this and FiniteIterable.
This means that all iterators model FiniteIterable by default, and the type must somehow learn to be infinite. How? You can specialize is_infinite. Fortunately, tools for creating incrementors and spacing accept the optional parameter IsInfinite, so this is easy to do. This is what the zeroes class now looks like:
By adding the FiniteIterable concept, we give algorithms that need a limb to test this at the compilation stage.
Now we need to divide the intervals into categories. In theory, either it is infinite or finite - is not it? Actually, no. Take istream. It may be finite, it may not be. Normally the flow stops, but sometimes ...
The situation is complicated. Is it necessary to prohibit the transfer of istream to the algorithm only because it can be infinite?
With infinite intervals, there is such a difficulty: all iterators and all incrementors have a related difference_type. Alexander Stepanov writes about this:
It turns out that we need a whole type of infinite size. Is there a solution to this problem?
I, of course, do not like everything that slows down the work of the algorithms, so std :: ptrdiff_t can be left as the default difference_type. In addition, you need to develop interval interfaces so that users can specify a different difference_type if they care about overflow. Therefore, I like options 4 and 5. Other library types like bigint or safe_int with certain restrictions would be nice to be able to apply - if the user could specify their use, changing the speed to security when he needs it.
Perhaps, reading the previous posts, you were too optimistic: everything seemed to be starting to turn out, and now you are confused. But it seems to me that we have made good progress compared to where we started from. I described 5 problems with intervals using a couple of iterators. The new concept of incrementors solves 3 of them, the 4th problem (infinite intervals) can theoretically be solved by improving this concept. And there are several options for working with the 5th (overflow). At least, a start.
Some ask if I plan to bring my ideas to the C ++ Standardization Committee. Of course. When we get support for concepts in a language, there will be a need for a conceptualized version of STL, possibly operating in a different namespace.
In the meantime, I will discuss the issue on the SG9 (Ranges) mailing list (http://www.open-std.org/mailman/listinfo/ranges). This controversial issue will certainly be able to generate new ideas. Interested urge to join the discussion.
The author brought his ideas to the committee and is now engaged in their implementation.
Other articles of the cycle
Intervals in C ++, part 1: Intervals with limiters
Intervals in C ++, part 2: Infinite intervals
Intervals in C ++, part 3: we represent incrementors (Iterable)
Disclaimer : ideas in this post are more speculative than in previous ones. I will be glad to discuss .
In addition to the solved problems, which I mentioned in previous posts, there are still two. It:
- Some STL algorithms do not work at infinite intervals.
- Infinite or perhaps infinite intervals cause the difference_type to overflow
Infinite iterators
iota_range is an infinite interval of integers, starting with some value and lasting forever. This is a sorted direct interval. Here are the algorithms of binary search, working with sorted direct intervals, will not work with him. It is impossible to conquer infinity by dividing (a good phrase turned out)
')
Is it possible to fix the STL algorithms so that they do not break when receiving an infinite interval? In their current form, no - it is impossible at the compilation stage to transmit information that any of the iterators denotes an infinite interval. Think about this: the following code will work:
// : iota_range<bigint> rng; auto i = std::lower_bound(rng.begin(), std::next(rng.begin(), 10), 5); but this will work "forever":
// «» :'-( iota_range<bigint> rng; auto i = std::lower_bound(rng.begin(), rng.end(), 5); If rng.begin () has the same type as rng.end (), the two calls return the same instance of lower_bound. The function will not be able to determine whether it will work forever or not. But if it is possible to allow the signal iterator to be of a different type, we will be able to carry out this check at the compilation stage.
Suppose we have a type function (metafunction) called DenotesInfiniteSequence, which takes a pair of types (BeginType, EndType) and tells whether the sequence will be infinite. We have already determined that if BeginType and EndType are the same, then the DenotesInfiniteSequence should return false, since it will not be able to verify this in any way. But if they are different - for example, EndType will be of type unreachable_sentinel or something like that, then we will know at the compilation stage that the sequence is infinite.
Infinite intervals
Some intervals, by definition, will be infinite, even having an initial and final iterator of the same type.
// class zeros : public range_facade<zeros> { friend range_core_access; struct impl { bool sentinel; int current() const { return 0; } void next() {} bool equal(impl that) const { return sentinel == that.sentinel; } }; // begin() end() range_facade // begin_impl end_impl. impl begin_impl() const { return {false}; } impl end_impl() const { return {true}; } }; // Range CONCEPT_ASSERT(Range<zeros>()); int main() { // for_each(zeros(), [](int i) {/*...*/}); } I would like to immediately catch such errors, but, obviously, the binary function DenotesInfiniteSequence cannot cope with this. For zeros, the BeginType and EndType types will be the same, so the DenotesInfiniteSequence will return false.
Therefore, it is necessary to construct a unary function of the IsInfinite types that takes an interval type.
// , Iterable template<typename Iterable> struct is_infinite : std::integral_constant<bool, true-or-false> {}; It can be used to define the concept of FiniteIterable.
// Concept Lite template<typename T> concept bool FiniteIterable = Iterable<T> && !is_infinite<T>::value; Each FiniteIterable is iterable. There is a parallel hierarchy of refinements:

And all these concepts, by analogy with Range, do not need to be defined in the code. The finiteness is orthogonal to the Iterable hierarchy, and it can be queried separately.
But why FiniteIterable, and not InfiniteIterable? It's all about the algorithms and their requirements. There are no algorithms that require their interval arguments to be infinite. Therefore, it would be useless to be able to write InfiniteIterable. But an algorithm like lower_bound would like the interval to be finite. From this and FiniteIterable.
This means that all iterators model FiniteIterable by default, and the type must somehow learn to be infinite. How? You can specialize is_infinite. Fortunately, tools for creating incrementors and spacing accept the optional parameter IsInfinite, so this is easy to do. This is what the zeroes class now looks like:
// class zeros : public range_facade<zeros, true> { // ... IsInfinite ...................^^^^ // ... , ... }; // zeros – Range, Finite CONCEPT_ASSERT(Range<zeros>()); CONCEPT_ASSERT(!FiniteIterable<zeros>()); By adding the FiniteIterable concept, we give algorithms that need a limb to test this at the compilation stage.
Perhaps infinite intervals
Now we need to divide the intervals into categories. In theory, either it is infinite or finite - is not it? Actually, no. Take istream. It may be finite, it may not be. Normally the flow stops, but sometimes ...
The situation is complicated. Is it necessary to prohibit the transfer of istream to the algorithm only because it can be infinite?
We count the uncountable
With infinite intervals, there is such a difficulty: all iterators and all incrementors have a related difference_type. Alexander Stepanov writes about this:
DistanceType returns an integer type large enough to measure any sequence of successor applications that are valid for the type.
It turns out that we need a whole type of infinite size. Is there a solution to this problem?
- In C ++, a bigint is required - an integer type with infinite precision. In other languages it is. C ++ is an excellent language for creating libraries, and the library is simply asking for this topic. If there was such a type, it could be taken as the difference_type.
- Infinite intervals can use safe_int as difference_type. safe_int behaves like an int, but can represent infinity. It does not overflow. The two most difficult problems with overflow are the difference_type - indefinite behavior and the inability to say after the fact what went wrong. With safe_int, uncertainties can be avoided and subsequently find out what happened.
- You can offer an alternative implementation of safe_int, in which it throws an exception during an overflow.
- You could also see where the library uses the difference_type and allow the user to specify that another type will be used there. For example, the distance calculation algorithm API may take an interval and an optional initial value. It would by default work with difference_type {0}, but if you gave bigint to it, you would work with it differently, slower, but safer.
- You can ignore the problem. And those who care about overflow can use the counting interval adapter (https://github.com/ericniebler/range-v3/blob/master/include/range/v3/view/counted.hpp) to make sure that the iterations stop before the difference_type overflows.
- Something else that did not occur to me.
I, of course, do not like everything that slows down the work of the algorithms, so std :: ptrdiff_t can be left as the default difference_type. In addition, you need to develop interval interfaces so that users can specify a different difference_type if they care about overflow. Therefore, I like options 4 and 5. Other library types like bigint or safe_int with certain restrictions would be nice to be able to apply - if the user could specify their use, changing the speed to security when he needs it.
The result, and what to do next
Perhaps, reading the previous posts, you were too optimistic: everything seemed to be starting to turn out, and now you are confused. But it seems to me that we have made good progress compared to where we started from. I described 5 problems with intervals using a couple of iterators. The new concept of incrementors solves 3 of them, the 4th problem (infinite intervals) can theoretically be solved by improving this concept. And there are several options for working with the 5th (overflow). At least, a start.
Some ask if I plan to bring my ideas to the C ++ Standardization Committee. Of course. When we get support for concepts in a language, there will be a need for a conceptualized version of STL, possibly operating in a different namespace.
In the meantime, I will discuss the issue on the SG9 (Ranges) mailing list (http://www.open-std.org/mailman/listinfo/ranges). This controversial issue will certainly be able to generate new ideas. Interested urge to join the discussion.
The author brought his ideas to the committee and is now engaged in their implementation.
Other articles of the cycle
Intervals in C ++, part 1: Intervals with limiters
Intervals in C ++, part 2: Infinite intervals
Intervals in C ++, part 3: we represent incrementors (Iterable)
Source: https://habr.com/ru/post/265355/
All Articles