Single-layer perceptron for beginners
Recently, more and more articles began to appear on machine learning and neural networks. “Neural network wrote classical music”, “Neural network recognized interior style”, neural networks learned a lot, and on the wave of growing interest in this topic I decided to write at least a small neural network without having special knowledge and skills.
To my great surprise, I did not find the simplest and transparent examples à la "Hello world". Yes, there is a coursera and a terrific Andrew Ng, there are articles about neural networks on Habré (I advise you to stop here and read if you don’t know the basics), but there is no simple example with a code. I decided to create a perceptron for recognizing “AND” or “OR” in my favorite C ++ language. If it is interesting to you, welcome under kat.
So, what do we need to create such a network:
1) Basic knowledge of C ++.
2) Armadillo library of linear algebra.
In ArchLinux it is put simply:
Create two files: CMakeLists.txt and Main.cpp.
CMakeLists.txt is responsible for the configuration of the project and contains the following code:
Main.cpp:
This is a test case to check if everything is properly configured.
If everything works, then continue!
')
How does the neural network work and understand what is AND and what is OR? So it looks like:
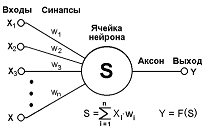
Strictly speaking, this is only a neuron, but at the same time it is the main concept of the network. First things first:
x1 and x2 and x ... are our inputs. Take the logical "AND"

Our input is A and B, that is, a 4 x 2 matrix, since it is more convenient to work with matrices.
w1 and w2 - “weights”, this is what the neural network will train. Usually there are one more scales than inputs, in our case there are 3 (+ bass).
Again the matrix: 3x1.
Y - output, this is our result, it will completely coincide with Q. Matrix 4x1. Matrices are very convenient to use with vectorization .
A neuron cell is a neuron that will learn w1 and w2. In our case, this will be a logistic regression . For learning w1 and w2, we will use the gradient descent algorithm.
Why logistic regression and gradient descent? Logistic regression is used because it is a logical task 0 / 1. Logistic regression (sigmoid) builds a smooth monotone non-linear function, having the shape of the letter "S":
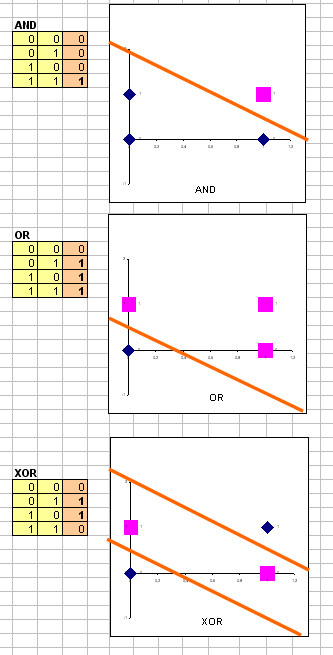
Linear regression is also widely known, but it is mainly used to classify large amounts of data. Gradient descent is the most common way of learning, it finds a local extremum by moving along the gradient (it just goes down).

This theoretical part ends, let's move on to practice!
So, the algorithm is as follows:
1) Set the input data
2) While the number of epochs has not come to an end (an alternative way: compare the prepared answers with those obtained and stop at the first match), multiply the weights by the input data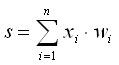 , apply logistic regression (sigmoid - sig),
, apply logistic regression (sigmoid - sig), 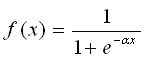 adjust weight using gradient descent.
adjust weight using gradient descent.
3) At the end, we launch the activation function (Axon), round off the matrix and display the result.
Perceptron is ready. Change Y to “OR” and make sure everything works correctly.
If you liked the article, then I will definitely write out how the multilayer perceptron works using the XOR example, explain the regularization, and we will add to the existing code.
Link to Main.cpp gist.github.com/Warezovvv/0c1e25723be1e600d8f2
Reference to the source of illustrations: robocraft.ru/blog/algorithm/558.html
To my great surprise, I did not find the simplest and transparent examples à la "Hello world". Yes, there is a coursera and a terrific Andrew Ng, there are articles about neural networks on Habré (I advise you to stop here and read if you don’t know the basics), but there is no simple example with a code. I decided to create a perceptron for recognizing “AND” or “OR” in my favorite C ++ language. If it is interesting to you, welcome under kat.
So, what do we need to create such a network:
1) Basic knowledge of C ++.
2) Armadillo library of linear algebra.
In ArchLinux it is put simply:
yaourt -S armadillo Create two files: CMakeLists.txt and Main.cpp.
CMakeLists.txt is responsible for the configuration of the project and contains the following code:
project(Perc) cmake_minimum_required(VERSION 3.2) set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11") set(CMAKE_BUILD_TYPE Debug) set(EXECUTABLE_NAME "Perc") file(GLOB SRC "*.h" "*.cpp" ) #Subdirectories option(USE_CLANG "build application with clang" ON) find_package(Armadillo REQUIRED) include_directories(${ARMADILLO_INCLUDE_DIRS}) set(CMAKE_RUNTIME_OUTPUT_DIRECTORY "${CMAKE_CURRENT_SOURCE_DIR}/bin") add_executable(${EXECUTABLE_NAME} ${SRC} ) TARGET_LINK_LIBRARIES( ${EXECUTABLE_NAME} ${ARMADILLO_LIBRARIES} ) Main.cpp:
#include <iostream> #include <armadillo> using namespace std; using namespace arma; int main(int argc, char** argv) { mat A = randu<mat>(4,5); mat B = randu<mat>(4,5); cout << A*Bt() << endl; return 0; } This is a test case to check if everything is properly configured.
cmake make ./bin/NeuroBot If everything works, then continue!
')
How does the neural network work and understand what is AND and what is OR? So it looks like:

Strictly speaking, this is only a neuron, but at the same time it is the main concept of the network. First things first:
x1 and x2 and x ... are our inputs. Take the logical "AND"

Our input is A and B, that is, a 4 x 2 matrix, since it is more convenient to work with matrices.
w1 and w2 - “weights”, this is what the neural network will train. Usually there are one more scales than inputs, in our case there are 3 (+ bass).
Again the matrix: 3x1.
Y - output, this is our result, it will completely coincide with Q. Matrix 4x1. Matrices are very convenient to use with vectorization .
A neuron cell is a neuron that will learn w1 and w2. In our case, this will be a logistic regression . For learning w1 and w2, we will use the gradient descent algorithm.
Why logistic regression and gradient descent? Logistic regression is used because it is a logical task 0 / 1. Logistic regression (sigmoid) builds a smooth monotone non-linear function, having the shape of the letter "S":

Linear regression is also widely known, but it is mainly used to classify large amounts of data. Gradient descent is the most common way of learning, it finds a local extremum by moving along the gradient (it just goes down).

This theoretical part ends, let's move on to practice!
So, the algorithm is as follows:
1) Set the input data
const int n = 2; // const int epoches = 100; // , "" w1 w2 double lr = 1.0; // mat samples({ 0.0, 0.0, 1.0, 1.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0 }); samples.set_size(4, 3); // mat targets{0.0, 0.0, 0.0, 1.0}; targets.set_size(4, 1); mat w; w.set_size(3,1); // -1 1 w.transform([](double val) { double f = (double)rand() / RAND_MAX; val= 1.0 + f * (-1.0 - 1.0); return val; }); 2) While the number of epochs has not come to an end (an alternative way: compare the prepared answers with those obtained and stop at the first match), multiply the weights by the input data
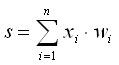 , apply logistic regression (sigmoid - sig),
, apply logistic regression (sigmoid - sig), 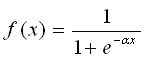 adjust weight using gradient descent.
adjust weight using gradient descent. for(int i = 0; i < epoches; i++) { mat z = samples * w; //Summator auto outputs = sig(z); //Gradient Descend w -= (lr*((outputs - targets) % sig_der(outputs)).t() * (samples) / samples.size ()).t(); std::cout << outputs << std::endl << std::endl; } 3) At the end, we launch the activation function (Axon), round off the matrix and display the result.
//Activate function mat a = samples * w; mat result = round(sig(a)); std::cout << result; Perceptron is ready. Change Y to “OR” and make sure everything works correctly.
If you liked the article, then I will definitely write out how the multilayer perceptron works using the XOR example, explain the regularization, and we will add to the existing code.
Link to Main.cpp gist.github.com/Warezovvv/0c1e25723be1e600d8f2
Reference to the source of illustrations: robocraft.ru/blog/algorithm/558.html
Source: https://habr.com/ru/post/265301/
All Articles