How the computer itself improved its code, or we program the programming process.
On the nose was inventing a topic for a diploma, the department was popular with various versions of ideas related to genetic algorithms, but I myself wanted to do something like that. And so the idea was born that gave rise to this project, namely the genetic optimizer of the program code.
The goal was quite ambitious - ideally, to make such a thing, which the program receives at the entrance, and then it turns it this way and that and tries to speed up its individual fragments in every possible way without human intervention, simultaneously gathering the basis for subsequent optimizations. I’ll say right away that although on the whole the task was solved, I couldn’t extract any practical benefits from it. However, some of the results obtained in the process seemed to me interesting enough to share.
')
For example, there is such a funny optimization of a set of arithmetic instructions (taken from some mathematical library that has come to hand) corresponding to the formulas: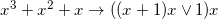
which gave me about 10% of acceleration on java with JIT turned off, at the same time, at first glance it’s not even obvious that these formulas are equivalent (WHERE IS HERE OR? THIS IS ALWAYS LEGAL!), although it is. Under the cut, I'll tell you exactly how such results were obtained and how the computer came up with a better code than the one that I myself could write.
I decided not to do anyhow what optimization, but the so-called “local” or peephole optimization. As a rule, this is the last stage through which modern optimizing compilers run programs, and in fact it is very simple - they search for given small linear sequences of instructions and change them to others that are optimal from their point of view. That is, here is some notorious replacement mov eax, 0 to xor eax eax - this is precisely the local optimization. The most interesting thing here is exactly how these replacement rules are constructed. They can be made by hand by specially trained and verbose assembler people, or searched by enumeration of instruction sets. Obviously, the first option is quite expensive (specially trained people will certainly want a lot of money) and ineffective (well, how many such sets can a person come up with and think of?), And the second is long, especially if you try to sort out long sequences.
This is where genetic algorithms come on the scene, which significantly reduces the search process.
About the genetic algorithms themselves, I will not tell here, I hope everyone at least in general terms represents what it is, and who does not represent - there are enough articles on this topic on Habré, for example, here . I’ll dwell only on how I applied them.
It is quite obvious that individuals in our case are code fragments, crossover operators and mutations must somehow modify the instructions included in them, and the fitness function selects the fastest options (since we’ll optimize the speed of execution). But how exactly this crossing should work?
Crossing and mutation of code fragments
From the idea to change arbitrary fragments, I refused very quickly. In this case, the probability of receiving an invalid code is very high, one that simply cannot be run. I chose JVM as my target architecture (because of the simplicity of both the bytecode itself and the means of manipulating it, although later I realized that it was not the most successful solution), but it has a fairly strict validator that simply will not allow the curve code to load. (eg causing stack emptying). Accordingly, the value of the fitness function for him to count will not work.
Therefore it was necessary to build a rather complicated system, almost a sort of mini-emulator JVM. For each instruction and each sequence, the initial and final states were determined. Specific values ​​were not calculated, only the types of operands were determined. That is, it was always possible to tell how many values ​​and which types were removed and put on the stack as a result of executing an arbitrary code fragment. Then, on the basis of this information, there was another set that could be replaced with this (in the case of mutation, it was created randomly, in the case of crossing, it was searched for in the second specimen), in order to preserve the correctness of the code, it had to be equivalent in terms of handling the state of the JVM — that is, removing from the stack and put back exactly the same number and types of values.
This does not apply to intermediate computations, that is, a fragment inside itself can do anything with the stack, but it should leave exactly the same state behind it.
Example:
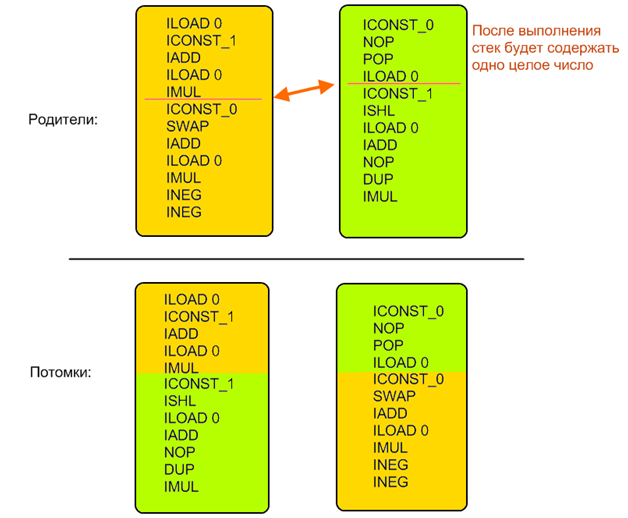
The initial generation was created according to the same rules - it had to change the state of the JVM in the same way as the original sequence of instructions. Thus, the correctness of individuals and their comparability were always maintained: since all individuals after their work always left the same state (values ​​of the same types on the stack in the same order), it was easy to compare the similarity of the obtained results with the reference ones: it was enough just to count the difference of two multidimensional vectors in which each value is a single register or a stack element (I occasionally use both Javas and non-Javas terminology here since, in principle, the algorithm is applicable to any bomu mind of the computer, and I myself checked it for several purposes).
Fitness function
What do we need from our individuals? And we need them to firstly consider the same results, and secondly - to do it faster than the original. And to check this - we need to run them.
We already have counted VM states at every step of the execution of our individuals. In particular, this gives us the necessary set of input data - that is, what registers must be filled and how many and what elements should be put on the stack so that everything works as it should. Well, we add the same code to the beginning of each individual, which will create this data, and by the end - which will record the results where we need it. The final value of the fitness function is made up of the distance between the result vectors and the acceleration factor compared to the original.
In the course of the research, it turned out that the “frontal” implementation leads to a rapid degeneration of the population, which is clogged with very short (and very fast) individuals that do not do anything useful (that is, instead of computing, for example, they simply empty the stack to the desired depth). gain due to length and speed. Therefore, we had to make it so that the speed starts to be taken into account only after the calculated results become sufficiently close to the reference ones.
In addition to the speed of work and equivalence of results, it was necessary to additionally control the length of individuals. Without such control in the population, the growth of the average length of an individual, up to 10–20 lengths of the initial code fragment, begins fairly quickly (approximately 50 generations). The appearance of such long individuals greatly slows down the genetic process, because, firstly, the code analysis time required for validation checks increases (the time of each iteration increases), and secondly, to obtain a solution, it is necessary to get rid of a large number of unnecessary instructions in the individual, which can take a significant number of generations (the total number of iterations is growing).
Since this work examines the optimization of execution speed, and not the size of the instruction set, the length ratio is used only for screening out too long candidates and applies to the formula only if the individual for which the fitness function is calculated is longer than the original one.
The final form of the fitness function:
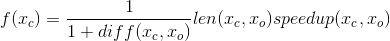
Here Xc is the tested individual, Xo is the original fragment, diff is the difference of the results vectors, len is the ratio is long, speedup is the ratio of the runtime.
A speedup is equal to one if diff is greater than a certain constant, that is, the speed starts to be taken into account only for an individual that considers almost correct values.
It is easy to verify that this function has the following properties:
Verification
In the course of the algorithm, each individual was tested for compliance with the results by giving the original fragment in several dozen test examples. This is a quick and fairly effective test, but it is clearly insufficient for rigorous proof of the equivalence of the resulting optimized sequence and the original one. To obtain such evidence, formal verification was used.
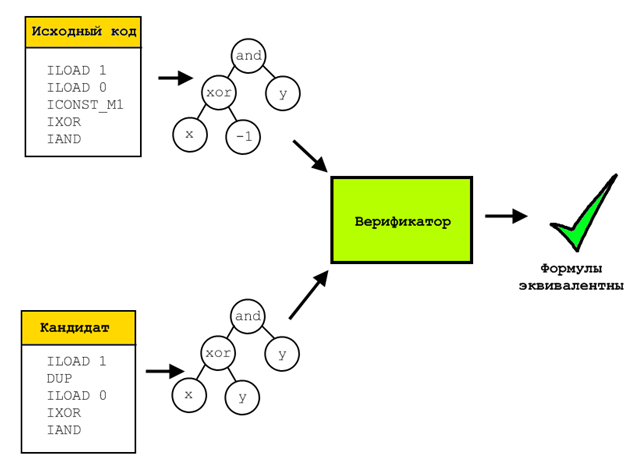
For this, for the verified and initial individuals, all their operations were represented in symbolic form, that is, after running through a special emulator, in each register / cell of the stack lay a symbolic representation of the formula calculated and written into it. Then all these formulas were compared using the Z3 SMT expression solver. Such a solver is able to prove that there is no set of input parameters on which the two formulas to be tested will give different results. If such a set exists, it will be built and presented.
Since this verification is quite a long process (it could take tens of minutes for one individual and a couple of simple mathematical expressions) only candidates for the final decision, that is, individuals with a fitness function greater than 1, were subjected to it.
However, it should be noted that in the course of the research, not a single candidate met, who would calculate everything correctly on test datasets but would be eliminated at the verification stage.
Examples
Genetic algorithms, like any other branch of machine learning, is an amazing thing, periodically forcing the programmer to clutch his head and shout “how, how did he do it?”. The piquancy here was added by the fact that in my case, with my help, the computer actually improves its programs itself in some unknown way, by inventing such things that I myself would not have thought of at once.
In general, I sometimes felt like a hero of this and similar comics:
Well, we drove our individuals through crosses and emulations, verified the equivalence of the results and what did we get? I will give a couple of examples of the optimizations I found.
Minimizing constants and other standard things.
First, the algorithm quite well finds all sorts of standard things on synthetic tests, such as removing unused calculations or folding constants, although I didn’t sharpen it specifically for this. For example, he quickly realized that x + 1 - 2 can be reduced to x - 1 :
It was:
It became:
All other examples are taken from real code, a special tool was written that parsed the compiled classes and looked for suitable sequences for optimization (that is, not containing branches and unsupported instructions).
Simplify Mathematical Expressions and Brackets
The example from the beginning of the article was reduced from 11 to 9 instructions: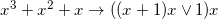 . At first glance, the expression is generally wrong, and having received it, I rushed to look for an error in the emulator code. But no, that's right, because the expression (x + 1) x is always even and non-negative, that is, the low-order bit is always zero, and in this case addition with the unit is equivalent to xor with it, and apparently works for some faster. The truth is only in the absence of JIT, if you turn it on then the quite expected ((x + 1) x + 1) x comes out on top. I don’t know why the OR (or XOR) version worked faster, but this result was regularly reproduced, including on different versions of Java and on different computers
In general, JIT in the case of Java brought a lot of headaches, and I even regretted that I chose this platform. It was never possible to be sure for one hundred percent, is it your optimization that has increased the speed, or is it a damn java-machine inside of you that turned something there? Of course, I studied all kinds of useful articles like Anatomy of incorrect micro-tests for performance evaluation , but I still had a lot of trouble with it. Very annoying is the sequential improvement in the code, depending on the number of launches. I started the fragment a hundred times - it works in the interpreter mode and gives one result, launched a thousand - turned on the JIT, translated it into a native code but didn’t optimize it much, launched ten thousand - JIT started picking something in this native code, as a result, the execution speeds change on orders and all this has to be taken into account.
Logical operators
However, in some places I even managed to jump. For example, the expression (x XOR -1) AND y The obvious enough optimization for it will be ! X and y , and this is exactly what the C ++ compiler will generate for you. But in Java's bytecode there is no bitwise single-operand operation, so the best option here would be (x XOR y) AND y . At the same time, the JIT is not thought out to this (it was checked by including the debug output on the JVM 1.6 server), which allows us to gain a little in speed.
Sly left shift feature
There was another fun result with the shift operator. Somewhere in the depths of BigInteger, the expression 1 << (x & 31) was found , the optimized version of which gave the algorithm 1 << x .
Again, grabbing the head, again looking for a bug - obviously, the algorithm took and threw out a whole significant piece of code. Until I thought of rereading the specification of operators more closely, in particular, it turned out that the << operator uses only 5 low bits of its second operand. Therefore, an explicit & 31 is not needed in general, the operator will do it for you (I understand that the library classes in the baytkod are forced & left for compatibility with older versions, since this feature did not appear in the very first java).
Problems and conclusion
Having received my results, I began to think what to do with them further. And it was here that nothing was invented. In the case of Java, my optimizations are too small and unnoticeable to have a significant impact on the speed of the program as a whole, at least for those programs on which I could test all this (maybe some deep scientific calculations and will benefit significantly from replacing a couple of instructions and cuts the time of one cycle for a couple of nanoseconds). In addition, the effect is significantly eaten by the structure of the java machine itself, virtuality and JIT.
I tried to switch to other architectures. At first on x86, I got the first working version, but the assembler is too complicated there and I couldn’t write the code required for its verification. Then I tried to stick in the direction of the shaders, since then I worked in game dev, and added support for the pixel shader assembler. But there I just could not find a single suitable shader containing a good example of a sequence of instructions.
In general, I did not think of where to screw this thing. Although the feeling of when the computer turns out to be smarter than you and finds such optimization that you don’t even immediately understand how it works, I remembered for a long time.
The goal was quite ambitious - ideally, to make such a thing, which the program receives at the entrance, and then it turns it this way and that and tries to speed up its individual fragments in every possible way without human intervention, simultaneously gathering the basis for subsequent optimizations. I’ll say right away that although on the whole the task was solved, I couldn’t extract any practical benefits from it. However, some of the results obtained in the process seemed to me interesting enough to share.
')
For example, there is such a funny optimization of a set of arithmetic instructions (taken from some mathematical library that has come to hand) corresponding to the formulas:
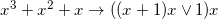which gave me about 10% of acceleration on java with JIT turned off, at the same time, at first glance it’s not even obvious that these formulas are equivalent (WHERE IS HERE OR? THIS IS ALWAYS LEGAL!), although it is. Under the cut, I'll tell you exactly how such results were obtained and how the computer came up with a better code than the one that I myself could write.I decided not to do anyhow what optimization, but the so-called “local” or peephole optimization. As a rule, this is the last stage through which modern optimizing compilers run programs, and in fact it is very simple - they search for given small linear sequences of instructions and change them to others that are optimal from their point of view. That is, here is some notorious replacement mov eax, 0 to xor eax eax - this is precisely the local optimization. The most interesting thing here is exactly how these replacement rules are constructed. They can be made by hand by specially trained and verbose assembler people, or searched by enumeration of instruction sets. Obviously, the first option is quite expensive (specially trained people will certainly want a lot of money) and ineffective (well, how many such sets can a person come up with and think of?), And the second is long, especially if you try to sort out long sequences.
This is where genetic algorithms come on the scene, which significantly reduces the search process.
About the genetic algorithms themselves, I will not tell here, I hope everyone at least in general terms represents what it is, and who does not represent - there are enough articles on this topic on Habré, for example, here . I’ll dwell only on how I applied them.
It is quite obvious that individuals in our case are code fragments, crossover operators and mutations must somehow modify the instructions included in them, and the fitness function selects the fastest options (since we’ll optimize the speed of execution). But how exactly this crossing should work?
Crossing and mutation of code fragments
From the idea to change arbitrary fragments, I refused very quickly. In this case, the probability of receiving an invalid code is very high, one that simply cannot be run. I chose JVM as my target architecture (because of the simplicity of both the bytecode itself and the means of manipulating it, although later I realized that it was not the most successful solution), but it has a fairly strict validator that simply will not allow the curve code to load. (eg causing stack emptying). Accordingly, the value of the fitness function for him to count will not work.
Therefore it was necessary to build a rather complicated system, almost a sort of mini-emulator JVM. For each instruction and each sequence, the initial and final states were determined. Specific values ​​were not calculated, only the types of operands were determined. That is, it was always possible to tell how many values ​​and which types were removed and put on the stack as a result of executing an arbitrary code fragment. Then, on the basis of this information, there was another set that could be replaced with this (in the case of mutation, it was created randomly, in the case of crossing, it was searched for in the second specimen), in order to preserve the correctness of the code, it had to be equivalent in terms of handling the state of the JVM — that is, removing from the stack and put back exactly the same number and types of values.
This does not apply to intermediate computations, that is, a fragment inside itself can do anything with the stack, but it should leave exactly the same state behind it.
Example:
The initial generation was created according to the same rules - it had to change the state of the JVM in the same way as the original sequence of instructions. Thus, the correctness of individuals and their comparability were always maintained: since all individuals after their work always left the same state (values ​​of the same types on the stack in the same order), it was easy to compare the similarity of the obtained results with the reference ones: it was enough just to count the difference of two multidimensional vectors in which each value is a single register or a stack element (I occasionally use both Javas and non-Javas terminology here since, in principle, the algorithm is applicable to any bomu mind of the computer, and I myself checked it for several purposes).
Fitness function
What do we need from our individuals? And we need them to firstly consider the same results, and secondly - to do it faster than the original. And to check this - we need to run them.
We already have counted VM states at every step of the execution of our individuals. In particular, this gives us the necessary set of input data - that is, what registers must be filled and how many and what elements should be put on the stack so that everything works as it should. Well, we add the same code to the beginning of each individual, which will create this data, and by the end - which will record the results where we need it. The final value of the fitness function is made up of the distance between the result vectors and the acceleration factor compared to the original.
In the course of the research, it turned out that the “frontal” implementation leads to a rapid degeneration of the population, which is clogged with very short (and very fast) individuals that do not do anything useful (that is, instead of computing, for example, they simply empty the stack to the desired depth). gain due to length and speed. Therefore, we had to make it so that the speed starts to be taken into account only after the calculated results become sufficiently close to the reference ones.
In addition to the speed of work and equivalence of results, it was necessary to additionally control the length of individuals. Without such control in the population, the growth of the average length of an individual, up to 10–20 lengths of the initial code fragment, begins fairly quickly (approximately 50 generations). The appearance of such long individuals greatly slows down the genetic process, because, firstly, the code analysis time required for validation checks increases (the time of each iteration increases), and secondly, to obtain a solution, it is necessary to get rid of a large number of unnecessary instructions in the individual, which can take a significant number of generations (the total number of iterations is growing).
Since this work examines the optimization of execution speed, and not the size of the instruction set, the length ratio is used only for screening out too long candidates and applies to the formula only if the individual for which the fitness function is calculated is longer than the original one.
The final form of the fitness function:
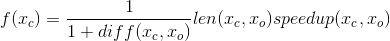
Here Xc is the tested individual, Xo is the original fragment, diff is the difference of the results vectors, len is the ratio is long, speedup is the ratio of the runtime.
A speedup is equal to one if diff is greater than a certain constant, that is, the speed starts to be taken into account only for an individual that considers almost correct values.
It is easy to verify that this function has the following properties:
- It is close to zero for initial random code fragments (the difference is large)
- It approaches unity as the calculated results converge with the reference ones.
- It is equal to one for the original fragment.
- All options with a fitness function of a larger unit are the potential results of the work of our algorithm, these are individuals who believe that it is necessary and at the same time faster / shorter
Verification
In the course of the algorithm, each individual was tested for compliance with the results by giving the original fragment in several dozen test examples. This is a quick and fairly effective test, but it is clearly insufficient for rigorous proof of the equivalence of the resulting optimized sequence and the original one. To obtain such evidence, formal verification was used.
For this, for the verified and initial individuals, all their operations were represented in symbolic form, that is, after running through a special emulator, in each register / cell of the stack lay a symbolic representation of the formula calculated and written into it. Then all these formulas were compared using the Z3 SMT expression solver. Such a solver is able to prove that there is no set of input parameters on which the two formulas to be tested will give different results. If such a set exists, it will be built and presented.
Since this verification is quite a long process (it could take tens of minutes for one individual and a couple of simple mathematical expressions) only candidates for the final decision, that is, individuals with a fitness function greater than 1, were subjected to it.
However, it should be noted that in the course of the research, not a single candidate met, who would calculate everything correctly on test datasets but would be eliminated at the verification stage.
Examples
Genetic algorithms, like any other branch of machine learning, is an amazing thing, periodically forcing the programmer to clutch his head and shout “how, how did he do it?”. The piquancy here was added by the fact that in my case, with my help, the computer actually improves its programs itself in some unknown way, by inventing such things that I myself would not have thought of at once.
In general, I sometimes felt like a hero of this and similar comics:
Well, we drove our individuals through crosses and emulations, verified the equivalence of the results and what did we get? I will give a couple of examples of the optimizations I found.
Minimizing constants and other standard things.
First, the algorithm quite well finds all sorts of standard things on synthetic tests, such as removing unused calculations or folding constants, although I didn’t sharpen it specifically for this. For example, he quickly realized that x + 1 - 2 can be reduced to x - 1 :
It was:
ILOAD 0 ICONST_1 IADD ICONST_2 ICONST_M1 IMUL IADD It became:
ILOAD 0 ICONST_1 ISUB All other examples are taken from real code, a special tool was written that parsed the compiled classes and looked for suitable sequences for optimization (that is, not containing branches and unsupported instructions).
Simplify Mathematical Expressions and Brackets
The example from the beginning of the article was reduced from 11 to 9 instructions:
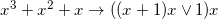. At first glance, the expression is generally wrong, and having received it, I rushed to look for an error in the emulator code. But no, that's right, because the expression (x + 1) x is always even and non-negative, that is, the low-order bit is always zero, and in this case addition with the unit is equivalent to xor with it, and apparently works for some faster. The truth is only in the absence of JIT, if you turn it on then the quite expected ((x + 1) x + 1) x comes out on top. I don’t know why the OR (or XOR) version worked faster, but this result was regularly reproduced, including on different versions of Java and on different computersIn general, JIT in the case of Java brought a lot of headaches, and I even regretted that I chose this platform. It was never possible to be sure for one hundred percent, is it your optimization that has increased the speed, or is it a damn java-machine inside of you that turned something there? Of course, I studied all kinds of useful articles like Anatomy of incorrect micro-tests for performance evaluation , but I still had a lot of trouble with it. Very annoying is the sequential improvement in the code, depending on the number of launches. I started the fragment a hundred times - it works in the interpreter mode and gives one result, launched a thousand - turned on the JIT, translated it into a native code but didn’t optimize it much, launched ten thousand - JIT started picking something in this native code, as a result, the execution speeds change on orders and all this has to be taken into account.
Logical operators
However, in some places I even managed to jump. For example, the expression (x XOR -1) AND y The obvious enough optimization for it will be ! X and y , and this is exactly what the C ++ compiler will generate for you. But in Java's bytecode there is no bitwise single-operand operation, so the best option here would be (x XOR y) AND y . At the same time, the JIT is not thought out to this (it was checked by including the debug output on the JVM 1.6 server), which allows us to gain a little in speed.
Sly left shift feature
There was another fun result with the shift operator. Somewhere in the depths of BigInteger, the expression 1 << (x & 31) was found , the optimized version of which gave the algorithm 1 << x .
Again, grabbing the head, again looking for a bug - obviously, the algorithm took and threw out a whole significant piece of code. Until I thought of rereading the specification of operators more closely, in particular, it turned out that the << operator uses only 5 low bits of its second operand. Therefore, an explicit & 31 is not needed in general, the operator will do it for you (I understand that the library classes in the baytkod are forced & left for compatibility with older versions, since this feature did not appear in the very first java).
Problems and conclusion
Having received my results, I began to think what to do with them further. And it was here that nothing was invented. In the case of Java, my optimizations are too small and unnoticeable to have a significant impact on the speed of the program as a whole, at least for those programs on which I could test all this (maybe some deep scientific calculations and will benefit significantly from replacing a couple of instructions and cuts the time of one cycle for a couple of nanoseconds). In addition, the effect is significantly eaten by the structure of the java machine itself, virtuality and JIT.
I tried to switch to other architectures. At first on x86, I got the first working version, but the assembler is too complicated there and I couldn’t write the code required for its verification. Then I tried to stick in the direction of the shaders, since then I worked in game dev, and added support for the pixel shader assembler. But there I just could not find a single suitable shader containing a good example of a sequence of instructions.
In general, I did not think of where to screw this thing. Although the feeling of when the computer turns out to be smarter than you and finds such optimization that you don’t even immediately understand how it works, I remembered for a long time.
Source: https://habr.com/ru/post/265195/
All Articles