About really BIG numbers (part 1)

The idea to write popularly about large numbers came while reading this article . It was about numbers, giants, having at least some physical meaning. And it ends with a reference to the Graham number. The number that will be the starting point of today's article. To imagine the scale of the disaster, I strongly recommend that you first read this article , which explains the number of Graham on the fingers of ^_TM - there the author very colorfully and consistently talks about the boundaries of perception, into which we pinch ourselves when talking about large numbers.To begin with, in order to prevent possible comments in the style of “but what for it is necessary, it still doesn’t have any practical sense at all” - the answer isIn general, as IngvarrT said in the discussion of an article about the number-giants, all the rest of the text comes down to the phrase “think about the mathematics”.

To begin with, it is necessary to clarify that when we speak of large numbers (not even BIG, but just big ones), we usually mean not a sequence of numbers forming this number, but a method (or method) with which this number is obtained. Of course, we can write the sextillion as 10000000000000000000000, but still it’s more usual to see 10 ²¹ . In this case, the method of describing the number will be the exponentiation operation (which looks like the number is written in superscript). The use of such methods makes it possible to reduce the recording of a number, leaving only the way of its formation (which, of course, is quite enough for performing mathematical operations on it). So we logically came to the conclusion that all conversations in BIG numbers come down to finding the most compact record of the largest possible number. So, "sho came up with these mathematicians."

We all know three basic arithmetic operations: addition ( a + b ), multiplication ( a × b ), exponentiation ( a ^b ). Have you ever thought that all these operations consistently flow from one another? And if so:
')






Generally, these operations are called hyperoperators. For addition, multiplication and exponentiation - 1st, 2nd and 3rd order respectively. The continuation of this series to higher orders suggests itself: a 4th order hyperoperator (tetration) is called sequential exponentiation:



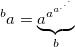
But for hyperoperators of higher orders, using such a system of designations will not work any more - it will be too cumbersome and confusing power-law towers. Therefore, to designate large numbers, other notation systems are used.

One of the most common is the Donald Knuth switch notation proposed in 1976. The principle of writing numbers follows from the sequence of hyperoperators and by and large is an explicit indication of the order of the hyperoperator. The usual exponentiation (3 order hyperoperator) is indicated by one arrow: a ↑ b , tetration - by two arrows a ↑↑ b, and so on. Here is how tetration is calculated:



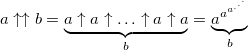
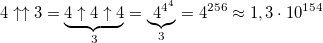
By changing just one digit, we get a huge increase in the value of a number:

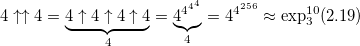- in this number more than 10 ¹⁵³ digits.

Adding another arrow we get a 4th order hyperoperator - pentation:




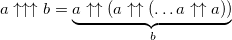
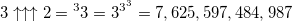
The change of one digit here leads to such a large increase in the value, that the epithets can and should not be chosen:
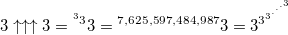- the height of the power tower is 7,625,597,484,987 elements ...
(this number is called tritri , and it will come in handy to us)
In order not to draw many arrows, an abbreviated notation is used: a ↑ ^_n b to designate a ↑↑ ... ↑ b with n arrows.

Here, you need to be extremely careful in estimating the growth rate of the function as the order of the hyperoperator increases (you obviously make a mistake in the lower direction) - if you don't pent three and hex three (well, just increase n by one), then we have to pent 3 times three, that is, three pent in three 7,625,597,484,987 times ... (but do not relax, all this is only the beginning, the very beginning).
By the way, you guessed it, what is the weakest point of Knut's switch notation? Yes, exactly n is the number of arrows. But what if it is so large that a regular number is no longer able to transmit it? A short digression: if three, pentirovanny in two, gives in to at least some understanding, then already three, pentirovannoe in three, it is impossible to imagine or realize. Not even stammering about the following orders of hyperoperators. This is a field of pure, uncomplicated abstract mathematics and, hell, it's fucking awesome!

The solution to Knut's notation is the Conway chain . They are used when even the Knut notation becomes too bulky to write the number. Remember the Graham number mentioned at the very beginning? Mark it with the whip arrows is simply impossible. The definition of the chain and its relationship with the Knut's arrows:



It seems to be the same thing. But the problem of the “number of arrows” in Conway’s chains is solved easily and gracefully: by adding another arrow. And each arrow draws the entire previous chain towards itself. Let's try to understand by example: take the tetration 3 → 3 → 2 (what it is: take the first two numbers and perform the exponentiation operation three times), add to the right → 2.
3 → 3 → 2 → 2 = 3 → 3 → (3 → 3 → 1 → 2) → 1 = 3 → 3 → (3 → 3) = 3 → 3 → 27
Adding just one arrow, we immediately went to the 27 order hyperoperator. And the Graham's number, which cannot be represented in Knut's switch notation, is written very concisely by Conway's chains: 3 → 3 → 64 → 2. But you can continue to add arrows and move on to increasingly unimaginable orders of numbers.

Ha! But is it right to draw as many arrows? And the numbers are growing too much ... In general, Jonathan Bowers introduced a massive notation (array notation), which in its maximally extended form is called BEAF (Bowers Exploding Array Function , explosive massive Bowers function, word game with English beaf - beef. It should be noted that Bowers, even in his scientific writings, has a special sense of humor). Its recording is very simple and resembles the already considered notations: 3 ↑↑↑ 3 = 3 → 3 → 3 = {3,3,3}. Another system of massive notation is also used, when the last element designating the order of the hyperoperator is transferred to the middle of the record, i.e. {3,3,2} = 3 {2} 3 (the logic is this - take two digits along the edges and do with them what is indicated in the middle).
At this stage, there are no differences between massive notation and Conway chains. But adding the fourth element of the array has a fundamentally different meaning, namely, the number of parentheses: {3,3,3} = {3,3,3,1}, {3,3,3,2} = {{3,3, 3}}.
{a, b, 1,2} = a {{1}} b = a {a {a .... a {a {a} a} a ... a} a} a, where b is the number of a, divergent from the center.

For clarity, let's see what happens when an element changes inside the central brackets “by one unit only”:
{3,3,1,2} = 3 {{1}} 3 = 3 {3 {3} 3} 3 = {3, 3, {3, 3, 3}} = {3, 3, tritri}
{3,3,2,2} = 3 {{2}} 3 = 3 {{1}} 3 {{1}} 3 = {3, {3, 3, tritri}, 1, 2} = 3 { 3 {3 ... 3 {3 {3} 3} 3 ... 3} 3} 3, where the number of triples diverging from the center to the edges is {3.3, tritri}.

In comparison with Conway's chains, the explosive growth in the number occurs at a stage earlier - if Conway has only the fourth number, he draws all the previous operations on himself, then Bowers has the third. A striking example of the above numbers:
in Conway, the third unit “eats” the remainder of the chain 3 → 3 → 1 → 2 = 3 → 3 = 27, then in Bowers it just “works” for its further growth: {3,3,1,2} = {3, 3, tritri}.

By the way, it was just an array of 4 elements. Add madness? It is not interesting to simply increase the number of array elements separated by commas, following the rules already formulated for working with them. Therefore, Bowers comes up with modified “brackets” in order to at least minimally visually “present” the numbers in massive notation. The fourth number in the array still remains with curly brackets, and then the uniform disgrace begins: the fifth - square brackets rotated 90 degrees, the sixth - rings around the previous design, the seventh - reverse angle brackets, the eighth - as three-dimensional square brackets ... In short, it is easier to show :

(even these pictures can be viewed here )

Do you think Bowers stopped there? As if not so. Well, what else can I think of in writing arrays? And you can note that there are commas ... Let them denote the elements of a one-dimensional array. And if you put between the numbers (1), then this is the transition to the next line, (2) - the transition to the next plane.
The square of the triples (“Dutritri”) is written as {3.3.3 (1) 3.3.3 (1) 3.3.3}.
Cube of triples ("Dimetry") - {3.3.3 (1) 3.3.3 (1) 3.3.3 (2) 3.3.3 (1) 3.3.3 (1) 3.3.3 (2) 3.3.3 (1) 3.3.3 (1) 3.3.3}.

This is how we simply moved from planar arrays to bulky ones (and notice, this is just a record of a certain number, which, because of its scale, required you to leave the plane simply in your writing!). Of course, later we introduce new notation for four-dimensional, five-dimensional “objects” (sorry, it’s already difficult to call these monstrous contractions). For example, & means “array from”: {10,100,2} & 10. That is, {10,100,2} is a tens array, or 10 ↑↑ 100 is an array of tens. Well, that is, you need to build ten to the tenth degree 100 times, build a grid with so many cells (and it will be in quantifying, that is, measuring measurements ... measurements (the word is repeated a hundred times)), then fill all the tens cells - and only then You can decide to solve this array.

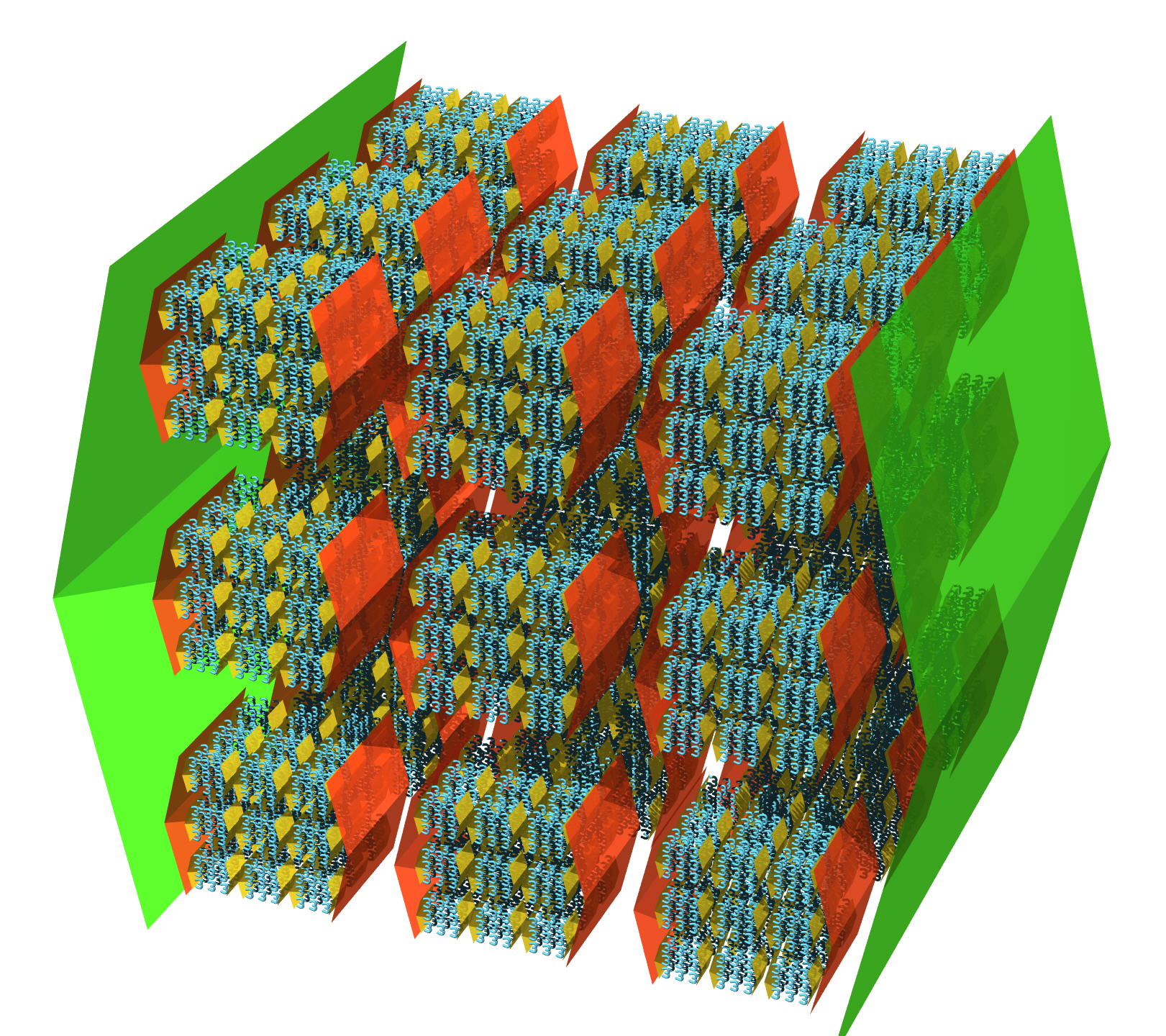
Think at least that's all? Nope Denote “legion” by forward slash (/). In the array {a, b, c, ... / 2}, the two is in the second legion. First we have to solve the first legion (to the left of the slash), and then take the number of elements in the chain “an array of ... an array of ... an array of ...", which turned out at the solution: {3.3 / 2} = 3 & 3 & 3 = {3,3,3} & 3. But if you take {3,3,3 / 3} = {3 & 3 & 3/2}. This time, tritri is not the number of elements in the array, but the number of elements in the chain 3 & 3 & ... & 3 & 3.
One more extension Bowers made by adding the symbol @ (a @ b stands for "a legion array of size a from b") and a backslash \ (l in gion). Well, everything is already clear here: {a, b \ 2} = a @ a @ a ... a @ a @ a (where a is repeated b times).

It is clear that the process of inventing new names for some operations cannot be infinite (lagions, legeons and ligions follow the legions and lugions, but it is obvious that this is nothing, given our scope), so Bowers made it easier - defined L as a progression from legions, lugions, lagions, legions and ligions: L1, L2, L3 ... And then the number is ahead of indices.
For example, for “computation” (it’s ridiculous, of course, to talk about computations on such scales) {L100,10} _10,10 you need to take the one-hundredth member in the progression “legions, lugions, lagions ...” and make an array of it in 10 dimensions. Then you need to remove one member, each time adding a chain from “10% 10% ...% 10” (where% is the L100-gion array from the number of tens that came out at the previous stage. And only after all the hundredth members (as well as L99, L98 and others like them, right up to \ and /) end, we can actually start solving the first array in a crazy array progression.

By the way, for 340 large numbers, Bowers introduced his own names, many of which by their insanity completely correspond to the calculation algorithms. Meet the UEMP MEAMEMEALOKKAPUVA: {{L100,10} _10.10 & L, 10} _10.10 .

<sup>Note for nerds:
Of course, Bowers defined a strict set of rules for performing operations on arrays.
Definitions:
- the first entry in the array is called “base” (base) - b;
- the second entry in the array is called “initial” (prime) - p;
- the first non-unit record after the initial one is called a “pilot”;
- the record of the array that immediately follows the pilot is called the “co-pilot”. It does not exist if the pilot is the first entry in his series;
- a structure is a part of an array, which consists of groups of lower dimension. It can be a record (X 0 ), a row (X 1 ), a plane (X 2 ), a region (X 3 ), etc., not to mention structures of higher dimension (X 5 , X 6 , etc. ) and tetration structures, for example, X ↑↑ 3. You can also continue with pentatation, hexation, etc. structures.
- “previous entry” (previous entry) is the entry that is formed in front of the pilot, but in the same row as the other previous entries. The “previous row” is the row that appears in front of the pilot row, but in the same plane as all the other previous rows, etc.
- The “prime block” (prime block) of the structure S is calculated by replacing all occurrences of X with p. For example, if S = X 3 , then the initial block will be p 3 or a cube with a side of length p. The initial block of the X x -structure will be a p p , p-hypercube with side length p.
- “airplane” includes the pilot, all previous entries, as well as the initial block of all previous structures;
- “passengers” are records in an airplane that are not a pilot or co-pilot;
- the value of the array is written as v (A) , where A is the array.
Calculation rules:
1. If p = 1, v (A) = b
2. If there is no pilot, then v (A) = b p
3. If the first and second does not apply, then:
- the pilot decreases by 1;
- the co-pilot receives the value of the original array with an initial value reduced by 1;
- each passenger becomes b;
- the rest of the array does not change
All the examples described above are subject to these simple rules.</sup>

As mentioned above, BEAF is far more powerful than Conway’s chains in its power, not to mention Knut's notation ... I wonder what's next?

And further we enter the field of philosophy rather than mathematics proper. All the notations described above are computable functions or functions that can be implemented on a Turing machine.

In the second part, we will look at non-computable functions : the zealous beavers problem, the Rado sigma function Σ (n), the Rayo number, BIG FOOT, and others, as well as the fast-growing hierarchy to see if there is a limit to this mathematical insanity.

Used materials:
1. The main site on googologiya: http://googology.wikia.com/wiki/Googology_Wiki
2. Jonathan Bowers Infinite Scratches
3. Exploding Array Function