How to easily understand logistic regression
Logistic regression is one of the statistical classification methods using the linear Fisher discriminant. It also ranks among the top frequently used algorithms in data science. In this article, the essence of logistic regression is described so that it will become clear even to people who are not very close to statistics.

Unlike conventional regression, the logistic regression method does not predict the value of a numeric variable based on a sample of initial values. Instead, the value of a function is the probability that a given initial value belongs to a particular class. For simplicity, let's assume that we have only two classes (see Multiple Logistic Regression for problems with a large number of classes ) and the probability that we will determine the likelihood that some value belongs to the class "+". And of course
the likelihood that some value belongs to the class "+". And of course  . Thus, the result of the logistic regression is always in the interval [0, 1].
. Thus, the result of the logistic regression is always in the interval [0, 1].
')
The basic idea of logistic regression is that the source value space can be divided by a linear border (ie, a straight line) into two areas corresponding to the classes. So, what is meant by a linear boundary? In the case of two dimensions, this is simply a straight line without bends. In the case of three, a plane, and so on. This limit is set depending on the available source data and the learning algorithm. For everything to work, the source data points must be divided by the linear boundary into the two areas mentioned above. If the source data points satisfy this requirement, then they can be called linearly separable. Look at the image.

This separating plane is called a linear discriminant, since it is linear in terms of its function, and allows the model to produce separation, discrimination of points into different classes.
But how is the linear border used in the logistic regression method for quantifying the probability of data points belonging to a certain class?
First, let's try to understand the geometric subtext of “dividing” the original space into two areas. Take for simplicity (as opposed to the 3-dimensional graph shown above) two source variables -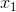 and
and 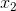 , then the function corresponding to the boundary takes the form:
, then the function corresponding to the boundary takes the form:
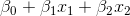
Consider the point . Substituting values
. Substituting values 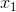 and
and 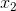 to the boundary function, we get the result
to the boundary function, we get the result 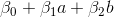 . Now, depending on the position
. Now, depending on the position  Three options should be considered:
Three options should be considered:
So, we have a function with the help of which it is possible to get a value within (-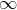 ,
, 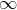 ) having a source data point. But how to convert the resulting value into the probability
) having a source data point. But how to convert the resulting value into the probability  whose limits are [0, 1]? The answer is using the odds ratio (OR) function.
whose limits are [0, 1]? The answer is using the odds ratio (OR) function.
Denote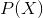 probability of an event occurring
probability of an event occurring 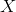 . Then, the odds ratio (
. Then, the odds ratio ( 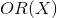 ) is determined from
) is determined from 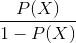 , and this is the ratio of the probabilities of whether an event will occur or not. It is obvious that probability and odds ratio contain the same information. But, while
, and this is the ratio of the probabilities of whether an event will occur or not. It is obvious that probability and odds ratio contain the same information. But, while 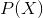 ranges from 0 to 1,
ranges from 0 to 1, 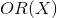 ranges from 0 to
ranges from 0 to 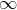 .
.
This means that another action is needed, since the boundary function we use produces values from -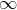 before
before 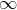 . Next, calculate the logarithm
. Next, calculate the logarithm 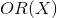 what is called the logarithm of the odds ratio. In the mathematical sense,
what is called the logarithm of the odds ratio. In the mathematical sense, 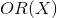 has limits from 0 to
has limits from 0 to 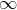 , but
, but  - from -
- from - 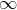 before
before 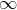 .
.
Thus, we have obtained a method for interpreting the results substituted into the boundary function of the original values. In the model used by us, the boundary function determines the logarithm of the odds ratio of the class "+". In essence, in our two-dimensional example, if there is a point , the logistic regression algorithm will look as follows:
, the logistic regression algorithm will look as follows:
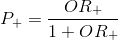
Getting value in step 1, you can combine steps 2 and 3:
in step 1, you can combine steps 2 and 3:
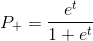
The right side of the equation above is called the logistic function. Hence the name given to this learning model.
The question remained unanswered: “How is the boundary function being studied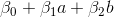 ? ”The mathematical basis of this is beyond the scope of the article, but the general idea is this:
? ”The mathematical basis of this is beyond the scope of the article, but the general idea is this:
Consider the function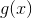 where
where  - data point of the training set. In simple form
- data point of the training set. In simple form 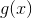 can be described as:
can be described as:
Function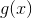 quantifies the likelihood that a training sample point is classified by the model in the correct way. Therefore, the average value for the entire training sample shows the probability that a random data point will be correctly classified by the system, regardless of the possible class.
quantifies the likelihood that a training sample point is classified by the model in the correct way. Therefore, the average value for the entire training sample shows the probability that a random data point will be correctly classified by the system, regardless of the possible class.
Let's just say - the logistic regression learning mechanism tries to maximize the average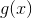 . And the name of this method is the maximum likelihood method. If you are not a mathematician, then you will be able to understand how optimization occurs, only if you have a good idea of what is being optimized.
. And the name of this method is the maximum likelihood method. If you are not a mathematician, then you will be able to understand how optimization occurs, only if you have a good idea of what is being optimized.

The basic idea of logistic regression
Unlike conventional regression, the logistic regression method does not predict the value of a numeric variable based on a sample of initial values. Instead, the value of a function is the probability that a given initial value belongs to a particular class. For simplicity, let's assume that we have only two classes (see Multiple Logistic Regression for problems with a large number of classes ) and the probability that we will determine
 the likelihood that some value belongs to the class "+". And of course
the likelihood that some value belongs to the class "+". And of course  . Thus, the result of the logistic regression is always in the interval [0, 1].
. Thus, the result of the logistic regression is always in the interval [0, 1].')
The basic idea of logistic regression is that the source value space can be divided by a linear border (ie, a straight line) into two areas corresponding to the classes. So, what is meant by a linear boundary? In the case of two dimensions, this is simply a straight line without bends. In the case of three, a plane, and so on. This limit is set depending on the available source data and the learning algorithm. For everything to work, the source data points must be divided by the linear boundary into the two areas mentioned above. If the source data points satisfy this requirement, then they can be called linearly separable. Look at the image.

This separating plane is called a linear discriminant, since it is linear in terms of its function, and allows the model to produce separation, discrimination of points into different classes.
If it is impossible to produce a linear separation of points in the original space, it is worth trying to convert the feature vectors into a space with a large number of dimensions, adding additional interaction effects, higher degree terms, etc. Using a linear algorithm in such a space provides certain advantages for learning a non-linear function, since the boundary becomes non-linear when it returns to the original space.
But how is the linear border used in the logistic regression method for quantifying the probability of data points belonging to a certain class?
How is the separation
First, let's try to understand the geometric subtext of “dividing” the original space into two areas. Take for simplicity (as opposed to the 3-dimensional graph shown above) two source variables -
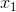 and
and 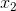 , then the function corresponding to the boundary takes the form:
, then the function corresponding to the boundary takes the form: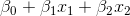
It is important to note thatand
are source variables, and the output variable is not part of the source space, unlike the linear regression method.
Consider the point
 . Substituting values
. Substituting values 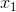 and
and 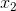 to the boundary function, we get the result
to the boundary function, we get the result 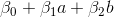 . Now, depending on the position
. Now, depending on the position  Three options should be considered:
Three options should be considered: lies in the area bounded by the points of the class "+". Then
lies in the area bounded by the points of the class "+". Then 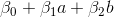 , will be positive, being somewhere within (0,
, will be positive, being somewhere within (0, 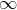 ). From a mathematical point of view, the larger the value of this value, the greater the distance between the point and the border. And this means a greater likelihood that
). From a mathematical point of view, the larger the value of this value, the greater the distance between the point and the border. And this means a greater likelihood that  belongs to the class "+". Consequently,
belongs to the class "+". Consequently,  will be within (0.5, 1].
will be within (0.5, 1]. lies in the area bounded by the dots of the class "-". Now,
lies in the area bounded by the dots of the class "-". Now, 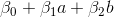 will be negative, being within (-
will be negative, being within (- 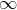 , 0). But, as in the case of a positive value, the greater the magnitude of the output value in the module, the greater the likelihood that
, 0). But, as in the case of a positive value, the greater the magnitude of the output value in the module, the greater the likelihood that  belongs to the class "-", and
belongs to the class "-", and  is in the interval [0, 0.5).
is in the interval [0, 0.5). lies on the border itself. In this case,
lies on the border itself. In this case, 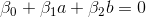 . This means that the model really cannot determine whether
. This means that the model really cannot determine whether  to the class "+" or to the class "-". And as a result,
to the class "+" or to the class "-". And as a result,  will be equal to 0.5.
will be equal to 0.5.
So, we have a function with the help of which it is possible to get a value within (-
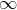 ,
, 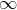 ) having a source data point. But how to convert the resulting value into the probability
) having a source data point. But how to convert the resulting value into the probability  whose limits are [0, 1]? The answer is using the odds ratio (OR) function.
whose limits are [0, 1]? The answer is using the odds ratio (OR) function.Denote
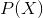 probability of an event occurring
probability of an event occurring 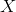 . Then, the odds ratio (
. Then, the odds ratio ( 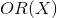 ) is determined from
) is determined from 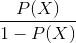 , and this is the ratio of the probabilities of whether an event will occur or not. It is obvious that probability and odds ratio contain the same information. But, while
, and this is the ratio of the probabilities of whether an event will occur or not. It is obvious that probability and odds ratio contain the same information. But, while 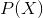 ranges from 0 to 1,
ranges from 0 to 1, 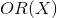 ranges from 0 to
ranges from 0 to 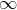 .
.This means that another action is needed, since the boundary function we use produces values from -
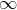 before
before 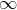 . Next, calculate the logarithm
. Next, calculate the logarithm 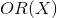 what is called the logarithm of the odds ratio. In the mathematical sense,
what is called the logarithm of the odds ratio. In the mathematical sense, 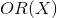 has limits from 0 to
has limits from 0 to 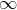 , but
, but  - from -
- from - 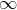 before
before 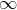 .
.Thus, we have obtained a method for interpreting the results substituted into the boundary function of the original values. In the model used by us, the boundary function determines the logarithm of the odds ratio of the class "+". In essence, in our two-dimensional example, if there is a point
 , the logistic regression algorithm will look as follows:
, the logistic regression algorithm will look as follows:- Step 1. Calculate the value.
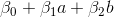 the boundary function (or, alternatively, the odds ratio function). For simplicity, we denote this value.
the boundary function (or, alternatively, the odds ratio function). For simplicity, we denote this value.  .
. - Step 2. Calculate the odds ratio:
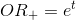 . (because
. (because  is the logarithm).
is the logarithm). - Step 3. Having value
 compute
compute  using simple dependencies.
using simple dependencies.
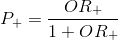
Getting value
 in step 1, you can combine steps 2 and 3:
in step 1, you can combine steps 2 and 3: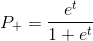
The right side of the equation above is called the logistic function. Hence the name given to this learning model.
How the function learns
The question remained unanswered: “How is the boundary function being studied
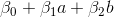 ? ”The mathematical basis of this is beyond the scope of the article, but the general idea is this:
? ”The mathematical basis of this is beyond the scope of the article, but the general idea is this:Consider the function
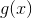 where
where  - data point of the training set. In simple form
- data point of the training set. In simple form 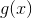 can be described as:
can be described as:if ais part of the "+" class,
(here
- output value obtained from the logistic regression model). If a
is part of the "-" class,
.
Function
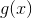 quantifies the likelihood that a training sample point is classified by the model in the correct way. Therefore, the average value for the entire training sample shows the probability that a random data point will be correctly classified by the system, regardless of the possible class.
quantifies the likelihood that a training sample point is classified by the model in the correct way. Therefore, the average value for the entire training sample shows the probability that a random data point will be correctly classified by the system, regardless of the possible class.Let's just say - the logistic regression learning mechanism tries to maximize the average
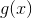 . And the name of this method is the maximum likelihood method. If you are not a mathematician, then you will be able to understand how optimization occurs, only if you have a good idea of what is being optimized.
. And the name of this method is the maximum likelihood method. If you are not a mathematician, then you will be able to understand how optimization occurs, only if you have a good idea of what is being optimized.Abstract
- Logistic regression is one of the statistical classification methods using the linear Fisher discriminant.
- The value of a function is the probability that a given initial value belongs to a particular class.
- logistic regression learning mechanism tries to maximize the mean
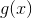 .
.
Source: https://habr.com/ru/post/265007/
All Articles