Finite models of reactions and shock forces in problems on the motion of systems with non-holding coupling

Introduction

In this article, we propose to consider an unconventional approach to solving problems on the motion of a mechanical system with a non-retaining bond. When solving such problems, it is necessary to analyze the conditions under which the system is released from communication, as well as to solve the issue of changing the nature of the system's movement when returning to communication, which is closely related to the concept of mechanical shock. For an example of how to formalize such a movement, consider the simple problem.

1. Statement of the problem

Inside a fixed smooth horizontal steel cylinder with a length of $L = 0.5$ , m is a smooth steel piston weight $m = 2.0$ , kg The piston is at rest and is pressed against the left end of the cylinder with a cylindrical spring of stiffness $c = 50$ N / m

')

Fig. 1. The design scheme for the problem of the movement of the piston

Spring has pre-tightening force $F_0 = 50$ , N. At the moment of time $t = 0$ horizontal force begins to act on the piston $\ vec P$ whose module is changed according to the law $P (t) = b \, t$ where $b = 25$ N / s. When the piston passes the first half of the cylinder force $\ vec P$ ceases to act.

Required to find the law of motion of the piston $x (t)$ . Coefficient of recovery when the piston hits the left end of the cylinder $k = \ frac {5} {9}$ .

2. Numerical and analytical solution of the problem

2.1. Determining the time of the beginning of the movement of the piston

We make the differential equation of motion of the piston

$m \, \ ddot x = P - F_e + N$

Where $F_e$ - the force of elasticity acting from the spring and equal to $F_e = c \, x + F_0$ ; $N \ ge 0$ - the reaction acting from the end of the cylinder. We come to the equation

$m \, \ ddot x = b \, t - c \, x - F_0 + N$

Obviously, the movement of the piston will begin only at that moment in time when the force $\ vec P$ will reach a value greater than the force of the initial tightening of the spring. Find this moment in time, putting the piston at rest

$x = 0$

Equation (2) describes a constraint constraining the motion of a cylinder. Substituting (2) into (1), we find the magnitude of the bond reaction

$N (t) = F_0 - b \, t$

Piston movement will start at time $t_1$ when it ceases to press on the end of the cylinder, that is, when $N (t_1) = 0$ . From here we receive the moment of the beginning of movement

$t_1 = \ frac {F_0} {b}$

2.2. The law of motion of the piston under the force of P ( t )

Given the task data $t_1 = 2$ c. With $t & gt; t_1$ we introduce a new countdown $\ tau$ such that $t = \ tau + t_1$ equation (1) takes the form

$\ ddot x + \ omega_0 ^ 2 \, x = \ frac {b} {m} \, \ tau + \ frac {b} {m} \, t_1 - \ frac {F_0} {m}$

Where $\ omega_0 = \ sqrt {\ frac {c} {m}}$ - natural frequency of oscillation of the piston. Taking into account the expression (3), we obtain some simplification.

$\ ddot x + \ omega_0 ^ 2 \, x = \ frac {b} {m} \, \ tau$

The general solution of this linear equation is

$x (\ tau) = x_0 (\ tau) + x_p (\ tau)$

Where $x_0 (\ tau) = C_1 \, \ cos \ omega_0 \ tau + C_2 \, \ sin \ omega_0 \ tau$ - the general solution of a homogeneous equation; $x_p (\ tau)$ partial solution of an inhomogeneous equation, which will be sought as a linear function

$x_p = A \, \ tau + B$

Substituting (5) into (4), we obtain the equations for the unknown coefficients A and B (5)

$\ begin {align *} & amp; B = 0, \\ & amp; \ omega_0 ^ 2 \, A = \ frac {b} {m} \ end {align *}$

Taking into account (6), we obtain the general solution of equation (4)

$x (\ tau) = C_1 \, \ cos \ omega_0 \ tau + C_2 \, \ sin \ omega_0 \ tau + \ frac {b} {m \, \ omega_0 ^ 2} \, \ tau$

With $\ tau = 0$ we have zero initial conditions, on the basis of which we determine the values of the integration constants in (7)

$C_1 = 0, \ quad C_2 = - \ frac {b} {m \, \ omega_0 ^ 3}$

We finally get for $t & gt; t_1$

$x_1 (t) = \ frac {b} {m \, \ omega_0 ^ 2} \, \ left [t - t_1 - \ frac {1} {\ omega_0} \, \ sin \ left (\ omega_0 \, (t - t_1) \ right) \ right]$

Solving a numerically transcendental equation

$\ frac {L} {2} = \ frac {b} {m \, \ omega_0 ^ 2} \, \ left [t_2 - t_1 - \ frac {1} {\ omega_0} \, \ sin \ left (\ omega_0 \, (t_2 - t_1) \ right) \ right]$

Find a moment in time $t_2$ when the piston reaches the middle of the cylinder.

$t_2 = 2.564, \, \ rm c$

2.3. Piston movement after the termination of the action P ( t ) before the collision

At the moment of time $t_2$ strength $\ vec P$ stops, and the equation of motion of the piston takes the form

$\ ddot x + \ omega_0 ^ 2 \, x = - \ frac {F_0} {m}$

Solving it under initial conditions $x_1 (t_2) = \ frac {L} {2} = 0.25, \ quad \ dot x_1 (t_2) = v_2 = 0.974$ get solution for $t & gt; t_2$

$x_2 (t) = \ left (\ frac {L} {2} + \ frac {F_0} {m \, \ omega_0 ^ 2} \ right) \, \ cos \ left (\ omega_0 (t - t_2) \ right ) + \ frac {v_2} {\ omega_0} \, \ sin \ left (\ omega_0 (t - t_2) \ right) - \ frac {F_0} {m \, \ omega_0 ^ 2}$

From (9) we find that the piston will move forward a distance $x _ {\ max} = 0.265$ , m, and then begins to move in the opposite direction, hitting the left end of the cylinder at the moment of time $t_3 = 2.726 c$ with speed $v_3 = \ dot x_2 (t_3) = -3.874$ , m / s

2.4. Piston movement after collision with cylinder

In accordance with the classical theory of impact, with a collinear impact of the body on a fixed barrier, the equation for the recovery coefficient

$k = - \ frac {u_n} {v_n}$

Where $k$ - coefficient of recovery; $v_n$ - the projection of the rate of penetration of the body into an obstacle on the normal to its surface; $u_n$ - projection of the speed of rebound of a body from an obstacle to the normal to its surface. Thus, after the first collision, the piston will gain speed

$u_1 = -k \, v_3$

and in accordance with equation (8), with $t & gt; t_3$ will move by the law

$x_3 (t) = \ frac {F_0} {m \, \ omega_0 ^ 2} \, \ left (\ cos \ left (\ omega_0 (t - t_3) \ right) - 1 \ right) - \ frac {k \ , v_3} {\ omega_0} \, \ sin \ left (\ omega_0 (t - t_3) \ right)$

At some point in time $t_4$ the next collision will occur after which the piston will move according to the law.

$x_4 (t) = \ frac {F_0} {m \, \ omega_0 ^ 2} \, \ left (\ cos \ left (\ omega_0 (t - t_4) \ right) - 1 \ right) - \ frac {k ^ 2 \, v_3} {\ omega_0} \, \ sin \ left (\ omega_0 (t - t_4) \ right)$

After the n-th collision, the piston will move according to the law.

$x_ {n + 2} (t) = \ frac {F_0} {m \, \ omega_0 ^ 2} \, \ left (\ cos \ left (\ omega_0 (t - t_ {n + 2}) \ right) - 1 \ right) - \ frac {k ^ n \, v_3} {\ omega_0} \, \ sin \ left (\ omega_0 (t - t_ {n + 2}) \ right)$

Where $t_ {n + 2}$ - moment of impact, determined from the equation $x_ {n + 1} (t_ {n + 2}) = 0$ .

2.5. Piston Motion Graph

The obtained analytical dependencies, taking into account the initial data of the problem, give a graph of the dependence of the piston coordinate on time

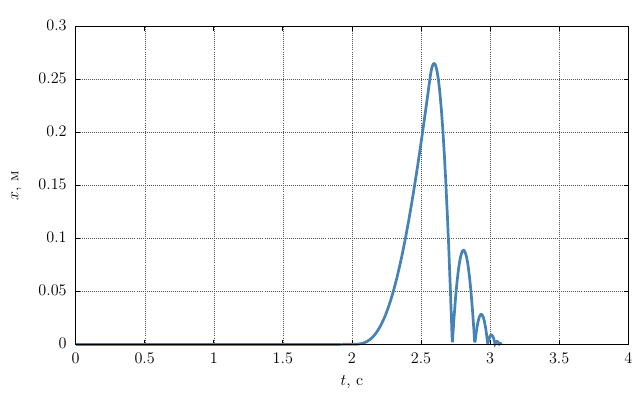
In the process of solving the problem, it can be seen that it is divided into several stages, for each of which several different differential equations are used. In addition, the algebraic equation (10) is used to calculate the piston speed after impact.

We consider a fairly simple system, in which only one detail is freed from communication and experiences periodic collisions with it. And if such details will be more, and the differential equations of their movement and the nature of the interaction more difficult? Is it possible to replace the differential-algebraic system of equations given above with a single differential equation that works in all cases? Can.

3. Nonlinear elastic-viscous shock force model

In our task, the coupling reaction is essentially an elastic force that prevents the piston from penetrating the barrier. The same applies to collisions. The literature describes an approach based on the assumption that when an impact body collides, only an insignificant part of them is subjected to elastic deformation. Such an approach allows one to describe the impact and contact interaction with the connection occurring through the mediation of a non-inertial, generally non-linear, power element, as shown in the figure below.

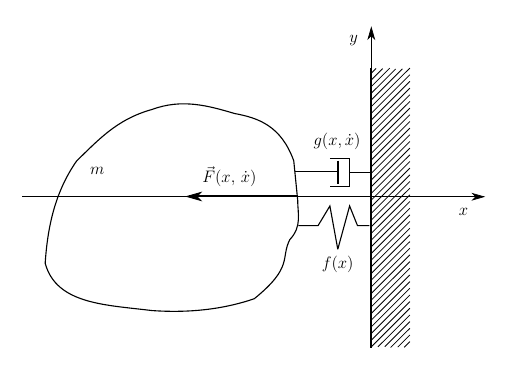
In this case, the collision process can be described by the following differential equation

$m \, \ ddot x = -F (x, \, \ dot x)$

where the impact force is described by the dependency type

$F (x, \, \ dot x) = \ begin {cases} & amp; 0, \ quad x \ le 0 \\ & amp; S (x, \, \ dot x), \ quad x & gt; 0 \ end {cases}$

at the same time, in the process of impact, the origin of coordinates is placed on the surface of the obstacle. The behavior of the system upon impact is largely determined by the type of dependence $S (x, \, \ dot x)$ which search at different times was carried out by different researchers. The Kelvin-Focht linear model, which gives expression, is widely known.

$S (x, \, \ dot x) = c_k \, x + \ beta \, \ dot x$

Where $c_k$ - contact stiffness at the point of impact; $\ beta$ - dissipation coefficient, taking into account the viscosity of the material. However, in this model, with all its flaws, the recovery coefficient on impact (10) does not depend on the impact velocity, which contradicts the experimental data.

In the work, G. Borovin, R.V. Dyaghel, V.V. Lapshin. A nonlinear viscoelastic model of a collinear impact is proposed a model in accordance with which the modulus of the impact force is calculated by the formula

$S (x, \, \ dot x) = f (x) \, (1 + \ beta \, \ dot x)$

Where $f (x)$ - elastic component; $\ beta$ - dissipation coefficient, taking into account the viscosity of the material. The elastic component in (11) may linearly depend on the strain

$f (x) = c_k \, x$

for the case when the surfaces in the impact zone are flat and non-linear, in accordance with the Hertz quasistatic model

$f (x) = c_k \, x ^ {\ frac {3} {2}}$

for convex surfaces. Model (11) is called the non-linear elastic-viscous Hanta-Crossley model. In the work of G. Borovin, R. V. Dyagelya and V. V. Lapshin, a detailed analytical study of the impact process using the Hunt-Crossley model is given. I will confine myself to mentioning the fact that using model (11), we obtain the dependence of the recovery coefficient on the impact velocity, which is in good agreement with the experimental data. The figure below shows the dependence of the recovery coefficient on the impact velocity and the coefficient $\ beta$ .

Fig. 2. Dependence of the coefficient of recovery on the velocity of collision at different coefficients of dissipation

Let's try to use this model when solving our problem.

4. The solution of the problem numerically, using the model of Hunt-Crossley

If the reaction of the cylinder end face is translated into the category of active forces, then, based on the expression (11), we obtain the differential equation of motion

$m \, \ ddot x = P (t, x) - c \, x - F_0 + N (x, \, \ dot x)$

Considering that when a cylinder interacts with a bond $x \ le 0$ write the expression for the reaction of the end face of the cylinder

$N (x, \, \ dot x) = \ begin {cases} 0, \ quad x & gt; 0 \\ -c_k \, x \, \ left (1 - \ beta \, \ dot x \ right), \ quad x \ le 0 \ end {cases}$

Such a model well reflects the nature of the interaction of the piston and the cylinder with a static contact - the equality to zero of the speed in (13) gives an expression for the elastic force, which is essentially a support reaction.

According to the condition of the task effort $\ vec P (t)$ ceases to act when the piston passes through the middle of the cylinder; therefore, we define this dependence with the following function

$P (t, x) = \ begin {cases} b \, t \ quad x & lt; \ cfrac {L} {2}, \\ 0, \ quad x \ ge \ cfrac {L} {2} \ end {cases}$

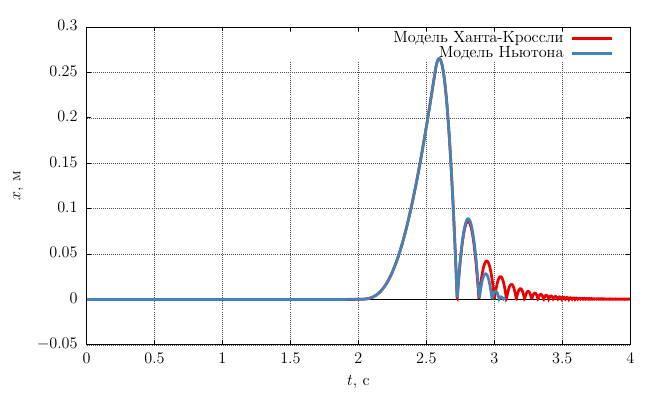
We take the following parameter values: contact stiffness $c_k = 1 \ cdot 10 ^ {10}$ N / m; dissipation coefficient is selected based on the recovery factor specified in the task $k = \ frac {5} {9}$ and estimates of the velocity of the first impact (3.8 m / s) obtained by us in the analytical solution of the problem - $\ beta = 0.31$ (according to the diagram in Figure 2). Numerical integration with zero initial conditions gives a result that we immediately compare with the analytical

And we see that the numerical solution of the problem using a continuous impact force model (13) gives a solution that coincides with the analytical one up to the second collision. After the second collision, the dependence of the recovery coefficient on the impact velocity, which is not taken into account by the classical Newton impact model that we used in the analytical solution of the problem, affects. Based on the graph in Figure 2, it can be said that the reduction coefficient increases with decreasing speed, which means the amplitude of the piston “bounces” from the end of the cylinder will be slightly larger than in the case of an analytical solution.

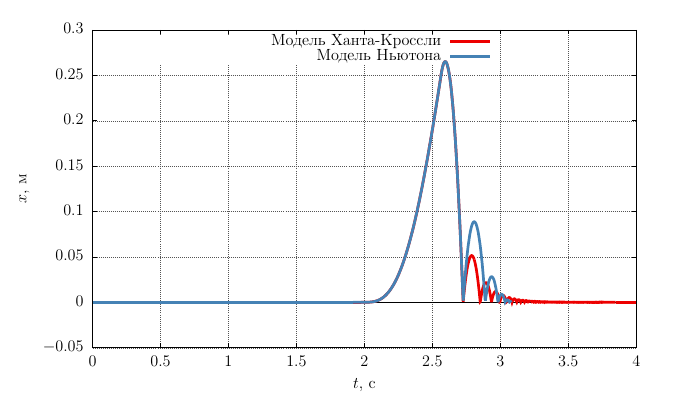
When the ratio $\ beta = 0.5$ we get faster damping of piston oscillations

Note that the result obtained is fully consistent with the analytical solution, and to study the motion of this system, only one differential equation is used (12)

findings

The approach considered by us, which consists in replacing reactions of a non-holding bond with active force (13), has an indisputable advantage: the motion is described by differential equations. We are spared the need to break the movement of the system into intervals, analyze the conditions for a return to communication, and “fit” the initial conditions. The solution of the problem is the continuous integration of this system of equations of motion over the entire time interval. This is especially true for the analysis of the movement of more complex mechanisms.

The disadvantage of the approach is the rigidity of equation (12). You probably noticed the great importance of contact stiffness. This forces us to use special methods for the numerical integration of ODE systems, in particular, in this case, the author used the Runge-Kutta-Fellberg method of order 5. This method has a variable integration step, the dependence of which on time looks like

Comparing this graph with the solution graph, it can be seen that the return of the piston to the link causes a decrease in the pitch.

In any case, this approach has the right to exist, and further research will show how justified its use is.

Thank you for attention!

Source: https://habr.com/ru/post/264867/

All Articles