On limitations in the applicability of the Minkowski metric in digital data processing
Once upon a time I came across an article on Habré in which people write how cool everything is and how well the Minkowski metric works. Time went on and on, and I wanted and wanted. Finally, the task to which I wanted to apply this miracle turned up, and this is what happened:

No-no-no, if I do it now, then you will not read the article. It will be. but later. And before that I want to describe the task that started it all:
')
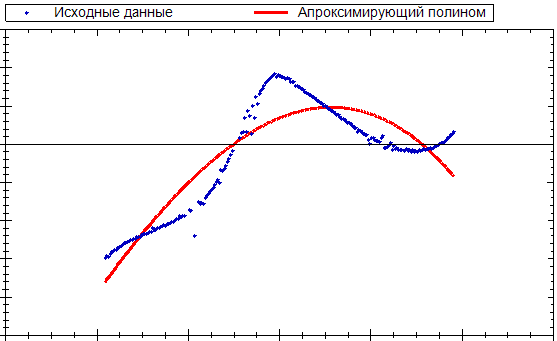

Right before you, there is a sufficiently high-quality approximation in the opinion of the algorithm. There is nothing to blame him: convergence to the resulting polynomial is extremely slow, the standard deviation changes reluctantly, and due to the small number of starting points (only about two hundred), the distribution of residuals in the first approximation looks like normal.
And so, in search of a universal criterion. which would allow me to distinguish a random sequence from a regular sequence (I know that this is a whole problem, but still), the idea came to use fractals. The fact is that the dimension of a random walk = 1.5. It is hoped that by calculating the dimension of the discrepancy curve, we get 1.5 + - reasonable values.
To calculate the Hausdorff dimension is still an idea, but with Minkowski everything is much simpler, although I had to sweat with it.
Let us apply the approach used in the starting article: changing the scale, we will count the number of rectangles N through which the curve passes. Having obtained the dependence log (N (e)) / log (e), we approximate directly with the help of the OLS. The metric we seek is the slope coefficient.
Unlike the original article, I do not scale up exponentially, but in arithmetic, there is too little data for the first. m_linearApproximator is a wrapper over the OLS, nothing clever and complex, and the OLS itself can be found either in the original article. either in MathNet.Numerics. The line if (count == 0) count = 1 arose due to the implementation. It covers the case when we have only one point.
All magic is in the fillBoxes method, this is where the squares are filled:
The raw data for me is a collection of points. The only thing that is known is that the process being measured is continuous, but the process itself is completely arbitrary: to random interference of different powers, interference can arise and disappear. In this case, the only way out is linear interpolation. As a consequence of the smallness of the input data, errors associated with the passage of a straight line through a lattice site are unacceptable.
Given these conditions, a universal solution that allows extension to any dimension is a step-by-step transition from square to square. (Immediately I warn you, the code shown does not take into account cases when the straight line is vertical or horizontal)
Let's test it on all possible lines:
It works and it is good. Let's take a square now. Argh, ran into what I warned about. But it does not matter, let's turn the square upside down, and then add degenerate cases:
Result 1.1 . Brr, what a strange thing. But no, of course, 2 is for a flat figure, for a rectangle, and not for its contour. Well, it is clear. Let's add a number of scales; 1.05; add more; aim for the unit.
It turns out that for a finite union of sets, the Minkowski dimension is the maximum for the dimension of each of the sets. Those. for a collection of direct dimensionality 1 . In other words, our result is absolutely correct.
Well, now you can prove that Popes is no different from the square. Since we represent the contour straight, then our area is divided either into a triangle or a square. about the square, we all know. What is the dimension of Minkowski at the square, we know - 2. And the triangle?
}{\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln&space;0.5&space;a-\ln\epsilon^2}{-\ln\epsilon}=2)
It is not strange, but also two. This, by the way, breaks the assumption in the original article that the fractal dimension reflects the non-smoothness of the curve. But this is by the way, the main thing is that in the end, the digitized pop Popes has the maximum dimension of 2 and 2.
Another interesting example. What is the dimension of the circle?
}{\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln&space;\pi&space;a-\ln\epsilon^2}{-\ln\epsilon}=2)
Too two. And the circle?
}{\ln(\epsilon)}=\lim\limits_{\epsilon\to0}\frac{\ln&space;\pi&space;a-\ln\epsilon}{-\ln\epsilon}=1)
Total: a circle, a square and a triangle (and Pope Lopez) are indistinguishable in us, this introduces serious difficulties in the model interpretation for the fractal dimension. Classical interpolation between the data on a straight line results in that the dimensions of the contour tend to 1, and the area to two. From this it is obvious that without some knowledge of a priori, its calculation loses its meaning. Well, our small test also showed that the orientation of a complex curve introduces strong perturbations in our calculations, and their evaluation is extremely difficult without understanding what the parameter itself shows.

No-no-no, if I do it now, then you will not read the article. It will be. but later. And before that I want to describe the task that started it all:
')


Right before you, there is a sufficiently high-quality approximation in the opinion of the algorithm. There is nothing to blame him: convergence to the resulting polynomial is extremely slow, the standard deviation changes reluctantly, and due to the small number of starting points (only about two hundred), the distribution of residuals in the first approximation looks like normal.
And so, in search of a universal criterion. which would allow me to distinguish a random sequence from a regular sequence (I know that this is a whole problem, but still), the idea came to use fractals. The fact is that the dimension of a random walk = 1.5. It is hoped that by calculating the dimension of the discrepancy curve, we get 1.5 + - reasonable values.
To calculate the Hausdorff dimension is still an idea, but with Minkowski everything is much simpler, although I had to sweat with it.
Let us apply the approach used in the starting article: changing the scale, we will count the number of rectangles N through which the curve passes. Having obtained the dependence log (N (e)) / log (e), we approximate directly with the help of the OLS. The metric we seek is the slope coefficient.
public double calculate(IEnumerable<KeyValuePair<double, double>> dataList) { double minY = Double.MaxValue, maxY = Double.MinValue; double minX = minY, maxX = maxY; foreach (var pair in dataList) { if (minY > pair.Value) minY = pair.Value; if (maxY < pair.Value) maxY = pair.Value; if (minX > pair.Key) minX = pair.Key; if (maxX < pair.Key) maxX = pair.Key; } m_bottomLeftY = minY; m_bottomLeftX = minX; return calculate(dataList, maxX, maxY); } public double calculate(IEnumerable<KeyValuePair<double, double>> dataList, double maxX, double maxY) { if( dataList.Count() < 2) return 0; for(int scaleNumber = StartSize; scaleNumber !=FinishSize; ++scaleNumber){ double XScale = (maxX - m_bottomLeftX) / scaleNumber; double YScale = (maxY - m_bottomLeftY) / scaleNumber; var enumerator = dataList.GetEnumerator(); fillBoxes( (ref double x, ref double y) => { var res = enumerator.MoveNext(); if (res) { x = enumerator.Current.Key; y = enumerator.Current.Value; } return res; }, XScale, YScale); int count = calculatedNumberBoxesAndReset(scaleNumber); if (count == 0) count = 1; m_boxesNumber[scaleNumber - StartSize] = Math.Log(count); } m_linearApproximator.approximate(m_scaleArgument, m_boxesNumber); return m_linearApproximator.resultPolinomal.a[1]; } double m_bottomLeftX, m_bottomLeftY; Unlike the original article, I do not scale up exponentially, but in arithmetic, there is too little data for the first. m_linearApproximator is a wrapper over the OLS, nothing clever and complex, and the OLS itself can be found either in the original article. either in MathNet.Numerics. The line if (count == 0) count = 1 arose due to the implementation. It covers the case when we have only one point.
All magic is in the fillBoxes method, this is where the squares are filled:
void fillBoxes(GetDataDelegate dataIterator, double stepX, double stepY) { double prevX=0, prevY=0, targetX=0, targetY=0; dataIterator(ref prevX, ref prevY); int indexY = FinishSize, indexX = FinishSize; int currentIndexX= calculateIndex(m_bottomLeftX, stepX, prevX), currentIndexY =calculateIndex(m_bottomLeftY, stepY, prevY) ; m_Boxes[currentIndexY, currentIndexX] = true; double[] CrossPosition = new double[2]; while (dataIterator(ref targetX, ref targetY)) { if(prevX == targetX && prevY == targetY) continue; bool isBottom = targetY - prevY < 0; bool isLeft = targetX - prevX < 0; double a = (targetY - prevY) / (targetX - prevX), fracA=1/a; double b = targetY - a * targetX; double leftBorder = m_bottomLeftX + currentIndexX * stepX, bottomBorder = m_bottomLeftY + currentIndexY * stepY; CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b; CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA; while ( (targetY < CrossPosition[0] == isBottom && Math.Abs(targetY - CrossPosition[0]) / stepY > 1E-9) || (targetX < CrossPosition[1] == isLeft && Math.Abs(targetX - CrossPosition[1]) / stepX > 1E-9) )// ? { if ( (bottomBorder - CrossPosition[0])/stepY <= 1E-9 && (CrossPosition[0] - bottomBorder - stepY)/stepY <= 1E-9) currentIndexX += isLeft ? -1 : 1; if ( (leftBorder-CrossPosition[1])/stepX <= 1E-9 && (CrossPosition[1] -leftBorder - stepX)/stepX <= 1E-9 ) currentIndexY += isBottom ? -1 : 1; m_Boxes[currentIndexY, currentIndexX] = true; leftBorder = m_bottomLeftX + currentIndexX * stepX; bottomBorder = m_bottomLeftY + currentIndexY * stepY; CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b; CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA; } prevY = targetY; prevX = targetX; } } The raw data for me is a collection of points. The only thing that is known is that the process being measured is continuous, but the process itself is completely arbitrary: to random interference of different powers, interference can arise and disappear. In this case, the only way out is linear interpolation. As a consequence of the smallness of the input data, errors associated with the passage of a straight line through a lattice site are unacceptable.
Given these conditions, a universal solution that allows extension to any dimension is a step-by-step transition from square to square. (Immediately I warn you, the code shown does not take into account cases when the straight line is vertical or horizontal)
Whole class
public class MinkowskiDimension { public MinkowskiDimension(int startSize, int finishSzie) { StartSize = startSize; FinishSize = finishSzie; } public MinkowskiDimension() { } public int StartSize { get { return m_startSize; } set { m_startSize = value; if (m_startSize < m_finishSize) { m_scaleArgument = new double[m_finishSize - m_startSize]; for (int i = 0; i != m_scaleArgument.Count(); ++i) m_scaleArgument[i] = - Math.Log(m_startSize + i); m_boxesNumber = new double[m_scaleArgument.Count()]; } } } int m_startSize; public int FinishSize { get { return m_finishSize; } set { m_finishSize = value; m_Boxes = new bool[value, value]; if (m_startSize < m_finishSize) { m_scaleArgument = new double[m_finishSize - m_startSize]; for (int i = 0; i != m_scaleArgument.Count(); ++i) m_scaleArgument[i] = Math.Log(m_startSize + i); m_boxesNumber = new double[m_scaleArgument.Count()]; } } } int m_finishSize; double[] m_scaleArgument; double[] m_boxesNumber; public double calculate(IEnumerable<KeyValuePair<double, double>> dataList) { double minY = Double.MaxValue, maxY = Double.MinValue; double minX = minY, maxX = maxY; foreach (var pair in dataList) { if (minY > pair.Value) minY = pair.Value; if (maxY < pair.Value) maxY = pair.Value; if (minX > pair.Key) minX = pair.Key; if (maxX < pair.Key) maxX = pair.Key; } m_bottomLeftY = minY; m_bottomLeftX = minX; return calculate(dataList, maxX, maxY); } public double calculate(IEnumerable<KeyValuePair<double, double>> dataList, double maxX, double maxY) { if( dataList.Count() < 2) return 0; for(int scaleNumber = StartSize; scaleNumber !=FinishSize; ++scaleNumber){ double XScale = (maxX - m_bottomLeftX) / scaleNumber; double YScale = (maxY - m_bottomLeftY) / scaleNumber; var enumerator = dataList.GetEnumerator(); fillBoxes( (ref double x, ref double y) => { var res = enumerator.MoveNext(); if (res) { x = enumerator.Current.Key; y = enumerator.Current.Value; } return res; }, XScale, YScale); int count = calculatedNumberBoxesAndIbit(scaleNumber); if (count == 0) count = 1; m_boxesNumber[scaleNumber - StartSize] = Math.Log(count); } m_linearApproximator.approximate(m_scaleArgument, m_boxesNumber); return m_linearApproximator.resultPolinomal.a[1]; } double m_bottomLeftX, m_bottomLeftY; void fillBoxes(GetDataDelegate dataIterator, double stepX, double stepY) { double prevX=0, prevY=0, targetX=0, targetY=0; dataIterator(ref prevX, ref prevY); int indexY = FinishSize, indexX = FinishSize; int currentIndexX= calculateIndex(m_bottomLeftX, stepX, prevX), currentIndexY =calculateIndex(m_bottomLeftY, stepY, prevY) ; m_Boxes[currentIndexY, currentIndexX] = true; double[] CrossPosition = new double[2]; while (dataIterator(ref targetX, ref targetY)) { if(prevX == targetX && prevY == targetY) continue; bool isBottom = targetY - prevY < 0; bool isLeft = targetX - prevX < 0; double a = (targetY - prevY) / (targetX - prevX), fracA=1/a; double b = targetY - a * targetX; double leftBorder = m_bottomLeftX + currentIndexX * stepX, bottomBorder = m_bottomLeftY + currentIndexY * stepY; CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b; CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA; while ( (targetY < CrossPosition[0] == isBottom && Math.Abs(targetY - CrossPosition[0]) / stepY > 1E-9) || (targetX < CrossPosition[1] == isLeft && Math.Abs(targetX - CrossPosition[1]) / stepX > 1E-9) )// ? { if ( (bottomBorder - CrossPosition[0])/stepY <= 1E-9 && (CrossPosition[0] - bottomBorder - stepY)/stepY <= 1E-9) currentIndexX += isLeft ? -1 : 1; if ( (leftBorder-CrossPosition[1])/stepX <= 1E-9 && (CrossPosition[1] -leftBorder - stepX)/stepX <= 1E-9 ) currentIndexY += isBottom ? -1 : 1; m_Boxes[currentIndexY, currentIndexX] = true; leftBorder = m_bottomLeftX + currentIndexX * stepX; bottomBorder = m_bottomLeftY + currentIndexY * stepY; CrossPosition[0] = (leftBorder + (isLeft ? 0 : stepX)) * a + b; CrossPosition[1] = (bottomBorder + (isBottom ? 0 : stepY) - b) * fracA; } prevY = targetY; prevX = targetX; } } int calculateIndex(double startvalue, double scale, double value) { double index = (value - startvalue) / scale; int intIndex = (int) index; return Math.Abs(index - intIndex) > 1E-9 || intIndex ==0 ? intIndex: intIndex -1; } int calculatedNumberBoxesAndIbit(int currentScaleSize) { int result=0; for (int i = 0; i != currentScaleSize; ++i) { for (int j = 0; j != currentScaleSize; ++j) { if (m_Boxes[i, j]){ ++result; m_Boxes[i, j] = false; } } } return result; } bool[,] m_Boxes; PolinomApproximation m_linearApproximator = new PolinomApproximation(1); } Let's test it on all possible lines:
[TestMethod] public void lineDimensionTest() { var m_calculator = new MinkowskiDimension(3, 10); var data = new List <KeyValuePair<double, double>>(); data.Add(new KeyValuePair<double, double>(0, 1)); data.Add(new KeyValuePair<double, double>(1, 5)); double result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); data.Add(new KeyValuePair<double, double>(2, 9)); result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); data.Clear(); data.Add(new KeyValuePair<double, double>(0, -1)); data.Add(new KeyValuePair<double, double>(1, -5)); data.Add(new KeyValuePair<double, double>(2, -9)); result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); data.Clear(); data.Add(new KeyValuePair<double, double>(0, -1)); data.Add(new KeyValuePair<double, double>(0.5, -3)); data.Add(new KeyValuePair<double, double>(2, -9)); result = m_calculator.calculate(data); if (Math.Abs(result - 1) > 1E-9) Assert.Fail(); } It works and it is good. Let's take a square now. Argh, ran into what I warned about. But it does not matter, let's turn the square upside down, and then add degenerate cases:
[TestMethod] public void squareDimensiontest() { var m_calculator = new MinkowskiDimension(3, 15); var data = new List<KeyValuePair<double, double>>(); data.Add(new KeyValuePair<double, double>(0, 1)); data.Add(new KeyValuePair<double, double>(1, 0)); data.Add(new KeyValuePair<double, double>(0, -1)); data.Add(new KeyValuePair<double, double>(-1, 0)); data.Add(new KeyValuePair<double, double>(0, 1)); double result = m_calculator.calculate(data); if (Math.Abs(result - 2) > 1E-9) Assert.Fail(); } Result 1.1 . Brr, what a strange thing. But no, of course, 2 is for a flat figure, for a rectangle, and not for its contour. Well, it is clear. Let's add a number of scales; 1.05; add more; aim for the unit.
It turns out that for a finite union of sets, the Minkowski dimension is the maximum for the dimension of each of the sets. Those. for a collection of direct dimensionality 1 . In other words, our result is absolutely correct.
Well, now you can prove that Popes is no different from the square. Since we represent the contour straight, then our area is divided either into a triangle or a square. about the square, we all know. What is the dimension of Minkowski at the square, we know - 2. And the triangle?
It is not strange, but also two. This, by the way, breaks the assumption in the original article that the fractal dimension reflects the non-smoothness of the curve. But this is by the way, the main thing is that in the end, the digitized pop Popes has the maximum dimension of 2 and 2.
Another interesting example. What is the dimension of the circle?
Too two. And the circle?
Total: a circle, a square and a triangle (and Pope Lopez) are indistinguishable in us, this introduces serious difficulties in the model interpretation for the fractal dimension. Classical interpolation between the data on a straight line results in that the dimensions of the contour tend to 1, and the area to two. From this it is obvious that without some knowledge of a priori, its calculation loses its meaning. Well, our small test also showed that the orientation of a complex curve introduces strong perturbations in our calculations, and their evaluation is extremely difficult without understanding what the parameter itself shows.
Source: https://habr.com/ru/post/264451/
All Articles