Magic of tensor algebra: Part 18 - Mathematical modeling of the Janibekov effect

Content

Introduction

The last article was supposed to be about the numerical simulation of the Janibekov effect, but I suddenly had the idea that this effect can be investigated qualitatively, even if it is rather approximate by the first Lyapunov method. However, numerical simulation is also a very interesting question, especially lying in the plane of my research tasks. Therefore, today we

Finally we will decide on how to use the Rodrig-Hamilton parameters to describe the orientation of the body in space.
Let us consider the forms of representation of the equations of motion of a free body: we will show how tensor equations can be turned into matrix and component ones.
Let us perform a simulation of the motion of a free solid at different ratios between the main moments of inertia and show how the Janibekov effect manifests itself.

1. Differential equations of free motion in tensor form

We have repeatedly considered these equations in vector form.

$\ begin {align *} & amp; m \, \ vec a_ {c} = \ sum \ vec F_k ^ {\, e} \\ & amp; \ mathbf I_c \, \ vec \ epsilon + \ vec \ omega \ times \ left (\ mathbf I_c \, \ vec \ omega \ right) = \ sum \ vec M_ {c} (\ vec F_k ^ {\, e}) \ end {align *}$

The vector form of the record is convenient for a general analysis of the nature of dependencies, it is customary and it shows what the specific term means. However, for the further transformation of equations into a form convenient for modeling, we turn to the tensor notation
')

$\ begin {align *} & amp; m \, \ left (\ ddot x ^ {\, i} + \ Gamma _ {\, kl} ^ {\, i} \, \ dot x ^ {\, k} \, \ dot x ^ {\, l} \ right) = X ^ {\, i} \\ & amp; I _ {\, j} ^ {\, i} \, \ dot \ omega ^ {j} + \ varepsilon ^ {\, ijk} \, \ omega _ {\, j} \, g _ {\, kl} \, I _ {\, p} ^ {\, l} \, \ omega ^ {\, p} = M ^ { i} \ end {align *}$

Where $x ^ {\, i}$ - contravariant coordinates of the center of mass of the body; $X ^ {\, i}$ - contravariant components of the main vector of external forces applied to the body; $M ^ {\, i}$ - contravariant components of the main moment of external forces applied to the body.

The system of equations (2) is already closed, integrating it can get the law of motion of the center of mass and the dependence of the angular velocity of the body on time. But, we will still be interested in the orientation of the body, so we supplement this system of equations

$2 \, \ varepsilon ^ {\, ijk} \, \ lambda _ {\, j} \, \ dot \ lambda _ {\, k} + 2 \, \ lambda_0 \, \ dot \ lambda ^ {\, i} - 2 \, \ lambda ^ {\, i} \, \ dot \ lambda_0 = \ omega ^ {\, i}$

Equation (3) is nothing more than the representation of the components of the angular velocity in terms of the orientation parameters of Rodrigues-Hamilton. We have already received this expression in previous articles . Now we will consider it as a differential equation relating the orientation parameters to the components of the angular velocity.

However, the Rodrigues-Hamilton parameters are redundant - there are four of them, and three coordinates are enough to describe the orientation of the body in space. And the number of unknowns in system (2), (3) exceeds the number of equations by one. So we have to supplement equations (2) and (3) with the equation of relation between the orientation parameters. In the article on the parameters of Rodrigues-Hamilton, we showed that it is convenient to describe the rotation of the body as a single quaternion, which is

$\ lambda_0 ^ 2 + \ lambda_1 ^ 2 + \ lambda_2 ^ 2 + \ lambda_3 ^ 2 = 1$

or, in tensor form

$\ lambda_0 ^ 2 + \ lambda _ {\, i} \, \ lambda ^ {\, i} = 1$

Differentiate (4) by time

$2 \, \ lambda_0 \, \ dot \ lambda_0 + \ dot \ lambda _ {\, i} \, \ lambda ^ {\, i} + \ lambda _ {\, i} \, \ dot \ lambda ^ {\, i } = 0$

Given the commutativity of the scalar product, we assume $\ dot \ lambda _ {\, i} \, \ lambda ^ {\, i} = \ lambda _ {\, i} \, \ dot \ lambda ^ {\, i}$ then

$\ lambda_0 \, \ dot \ lambda_0 + \ lambda _ {\, i} \, \ dot \ lambda ^ {\, i} = 0$

and there is a desired equation of communication. The complete system of equations for the motion of a free rigid body in tensor form will be

$\ begin {align *} & amp; \ dot x ^ {\, i} - v ^ {\, i} = 0 \\ & amp; m \, \ left (\ dot v ^ {\, i} + \ Gamma_ { \, kl} ^ {\, i} \, v ^ {\, k} \, v ^ {\, l} \ right) = X ^ {\, i} \\ & 2 \, \ varepsilon ^ { \, ijk} \, \ lambda _ {\, j} \, \ dot \ lambda _ {\, k} + 2 \, \ lambda_0 \, \ dot \ lambda ^ {\, i} - 2 \, \ lambda ^ { \, i} \, \ dot \ lambda_0 - \ omega ^ {\, i} = 0 \\ & amp; \ lambda_0 \, \ dot \ lambda_0 + \ lambda _ {\, i} \, \ dot \ lambda ^ {\ , i} = 0 \\ & amp; I _ {\, j} ^ {\, i} \, \ dot \ omega ^ {j} + \ varepsilon ^ {\, ijk} \, \ omega _ {\, j} \ , g _ {\, kl} \, I _ {\, p} ^ {\, l} \, \ omega ^ {\, p} = M ^ {i} \ end {align *}$

Pretty scary - (6) contains 13 nonlinear differential equations of the first order with 13 unknowns. It looks scary because of the general tensor notation, but when moving to specific coordinates, in our case Cartesian, the system (6) is much simpler.

2. The matrix form of the differential equations of motion of a rigid body in the Cartesian basis

We introduce the column vector of the phase coordinates of the body

$\ mathbf y = \ begin {bmatrix} \ mathbf x ^ T & amp; & amp; \ mathbf q ^ T & amp; & amp; \ mathbf v ^ T & amp; & amp; \ mathbf \ omega ^ T \ end {bmatrix} ^ T$

Where $\ mathbf x = \ begin {bmatrix} x_c & amp; & amp; y_c & amp; & amp; z_c \ end {bmatrix} ^ T$ and $\ mathbf v = \ begin {bmatrix} v_ {cx} & &; v_ {cy} & amp; & amp; v_ {cz} \ end {bmatrix} ^ T$ - position and speed of the center of mass of the body; $\ mathbf q = \ begin {bmatrix} \ lambda_0 & amp; & amp; \ lambda_1 & amp; & amp; \ lambda_2 & amp; & amp; \ lambda_3 \ end {bmatrix} ^ T$ and $\ mathbf \ omega = \ begin {bmatrix} \ omega_x & amp; & amp; \ omega_y & amp; & amp; \ omega_z \ end {bmatrix} ^ T$ - orientation and angular velocity of the body.

In the Cartesian basis, the metric tensor is represented by the unit matrix and the Christoffel symbols are zero, therefore the system of equations (6) is written in matrix form as

$\ begin {align *} & amp; \ mathbf {\ dot x} - \ mathbf v = \ mathbf 0 \\ & amp; 2 \, \ mathbf B \, \ mathbf {\ dot q} - \ mathbf D \, \ mathbf \ omega = \ mathbf 0 \\ & amp; m \ mathbf {\ dot v} = \ mathbf X \\ & amp; \ mathbf I_c \, \ mathbf {\ dot \ omega} + \ mathbf \ Omega \, \ mathbf I_c \, \ mathbf \ omega = \ mathbf M_c \ end {align *}$

where matrices are entered

$\ mathbf B = \ begin {bmatrix} \ lambda_0 & amp; & amp; \ lambda_1 & amp; & amp; \ lambda_2 & amp; & amp; \ lambda_3 \\ - \ lambda_1 & amp; & amp; \ lambda_0 & amp; & amp; - \ lambda_3 & amp; & amp; \ lambda_2 \\ - \ lambda_2 & amp; & amp; \ lambda_3 & amp; & amp; \ lambda_0 & amp; & amp; - \ lambda_1 \\ - \ lambda_3 & amp; & amp; - \ lambda_2 & amp; & amp; \ lambda_1 & amp; & amp; \ lambda_0 \\ {end {bmatrix}, \ quad \ mathbf D = \ begin {bmatrix} \ mathbf 0 ^ T \\ \ mathbf E \ end {bmatrix}, \ quad \ mathbf \ Omega = \ begin {bmatrix} 0 & amp; & amp; - \ omega_z & amp; & amp; \ omega_y \\ \ omega_z & amp; & amp; 0 & amp; & amp; - \ omega_x \\ - \ omega_y & amp; & amp; \ omega_z & amp; & amp; 0 \ end {bmatrix}$

Solving the system (7) with respect to the first derivatives, we obtain

$\ begin {align *} & amp; \ mathbf {\ dot x} = \ mathbf v \\ & amp; \ mathbf {\ dot q} = \ frac {1} {2} \, \ mathbf B ^ {- 1} \, \ mathbf D \, \ mathbf \ omega \\ & amp; \ mathbf {\ dot v} = \ frac {1} {m} \, \ mathbf X \\ & amp; \ mathbf {\ dot \ omega} = \ mathbf I_c ^ {- 1} \, \ left (\ mathbf M_c - \ mathbf \ Omega \, \ mathbf I_c \, \ mathbf \ omega \ right) \ end {align *}$

system of equations of motion in the form of Cauchy.

3. Simulation of the Janibekov effect

In the absence of external force factors, the right side of system (8) is zero, and the equation of motion of the center of mass is easily integrated, taking into account the initial conditions

$\ mathbf x (t) = \ mathbf x_0 + \ mathbf v_0 \, t$

The rotation of the nut is described by a system of seven first-order equations, which we obtain from (8), introducing the dimensionless moments of inertia $i_y = \ frac {I_y} {I_x}$ and $i_z = \ frac {I_z} {I_x}$

$\ begin {align *} & amp; \ dot \ lambda_0 = - \ frac {1} {2} \, \ left (\ lambda_1 \, \ omega_x + \ lambda_2 \, \ omega_y + \ lambda_3 \, \ omega_z \ right) \\ & amp; \ dot \ lambda_1 = \ frac {1} {2} \, \ left (\ lambda_0 \, \ omega_x + \ lambda_3 \, \ omega_y - \ lambda_2 \, \ omega_z \ right) \\ & amp; \ dot \ lambda_2 = - \ frac {1} {2} \, \ left (\ lambda_3 \, \ omega_x - \ lambda_0 \, \ omega_y - \ lambda_1 \, \ omega_z \ right) \\ & amp; \ dot \ lambda_3 = \ frac {1} {2} \, \ left (\ lambda_2 \, \ omega_x - \ lambda_1 \, \ omega_y + \ lambda_0 \, \ omega_z \ right) \\ & amp; \ dot \ omega_x = \ left (i_y - i_z) \, \ omega_y \, \ omega_z \\ & amp; \ dot \ omega_y = \ frac {i_z - 1} {i_y} \, \ omega_x \, \ omega_z \\ & amp; \ dot \ omega_z = \ frac {1 - i_y} {i_z} \, \ omega_x \, \ omega_y \ end {align *}$

For the numerical integration of system (9), we define the initial conditions

$\ begin {align *} & amp; \ lambda_0 (0) = 1, \ quad \ lambda_1 (0) = \ lambda_2 (0) = \ lambda_3 (0) = 0 \\ & amp; \ omega_x (0) = \ omega_0, \ quad \ omega_y (0) = \ Delta \ omega_y, \ quad \ omega_z (0) = 0 \ end {align *}$

Where $\ omega_0$ - the angular velocity of the nut after descending from the thread; $\ Delta \ omega_y$ - the initial perturbation of the angular velocity

With the values of the parameters $i_y = 2.0, \, i_z = 0.5, \, \ omega_0 = 1.0$ , glad / s $\ Delta \ omega_y = 1 \ cdot 10 ^ {- 10}$ , rad / s, the movement of the nut is as follows

Rodrigues-Hamilton orientation options

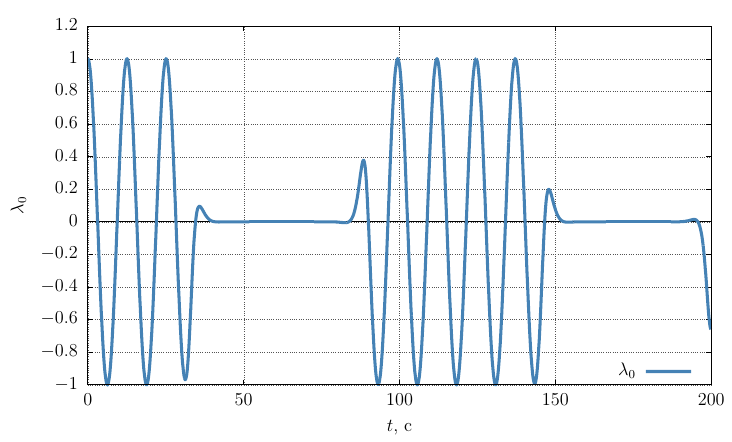
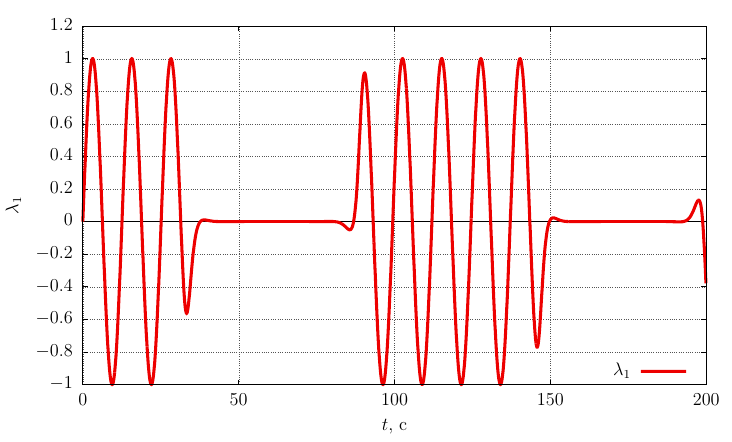
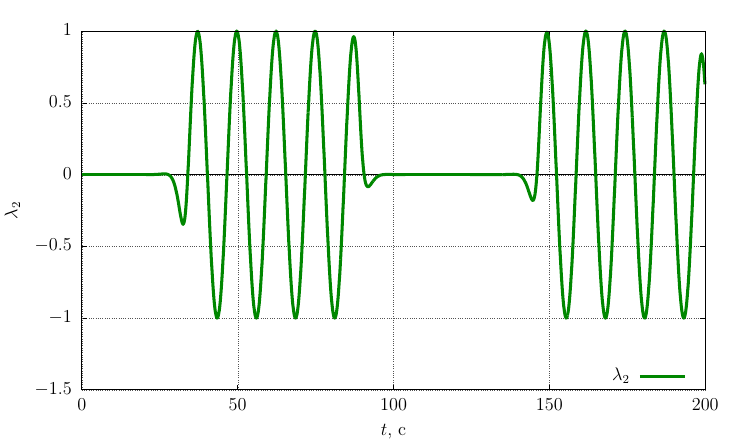
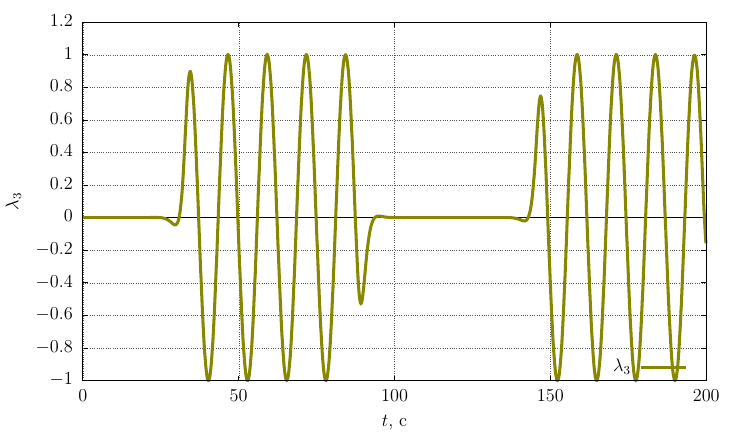
The projections of the angular velocity on its own axis

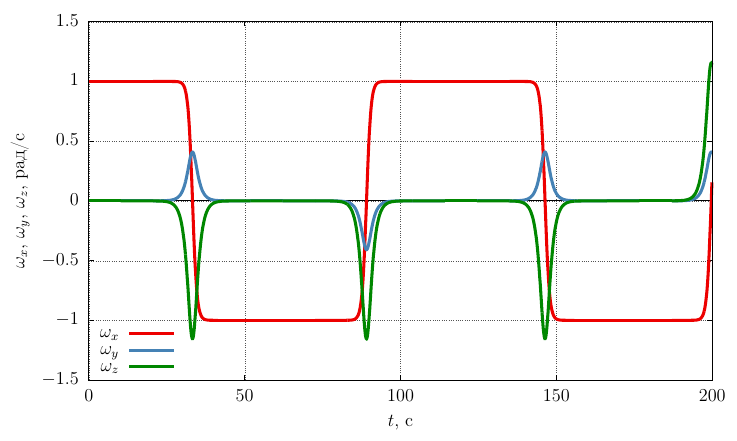
From the graphs it is clear that when $I_y & gt; I_x & gt; I_z$ , a very slight perturbation of the vector of angular velocity leads to a periodic avalanche-like change in the orientation of the nut in space.

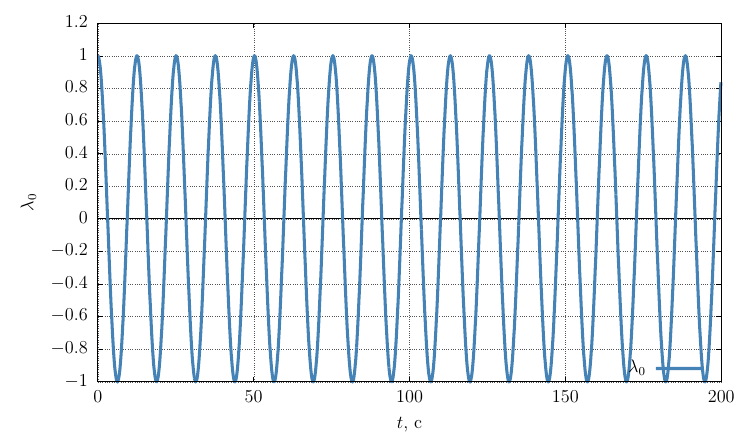
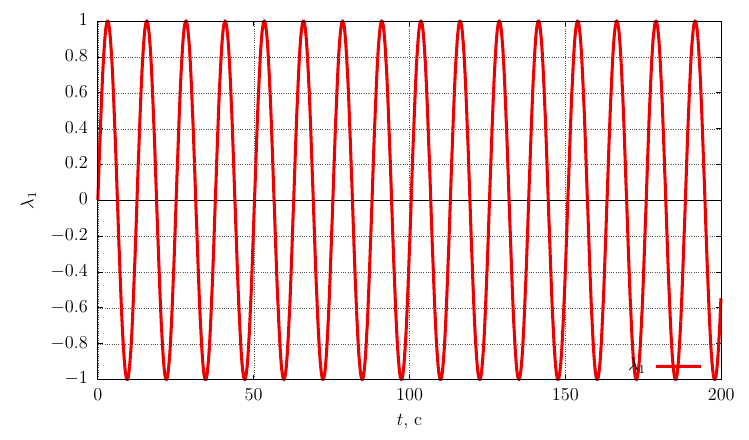
Let us compare the result obtained with the body motion twisted around the axis with the maximum moment of inertia, that is, we set $I_x & gt; I_y = I_z$ by setting the following parameter values $i_y = 0.5, \, i_z = 0.5, \, \ omega_0 = 1.0$ , glad / s $\ Delta \ omega_y = 1 \ cdot 10 ^ {- 2}$ , glad / s

Rodrigues-Hamilton orientation options

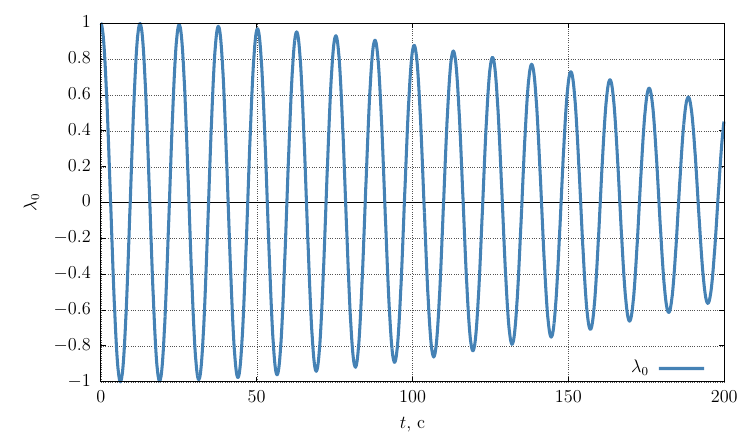
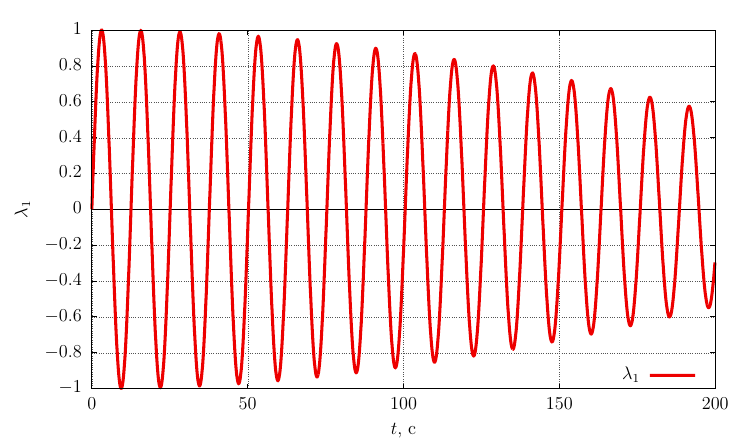
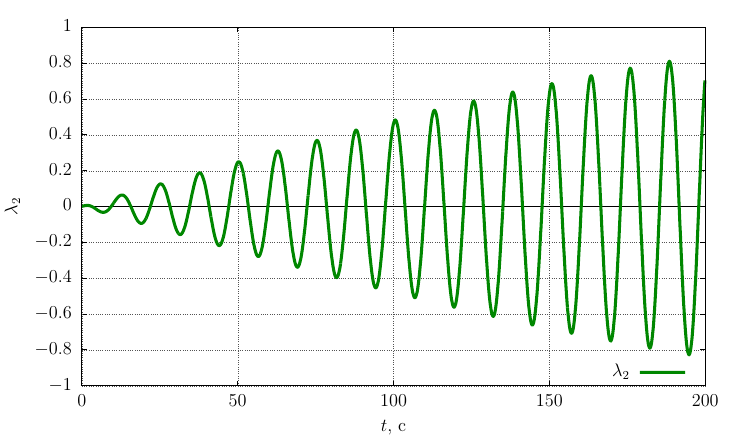
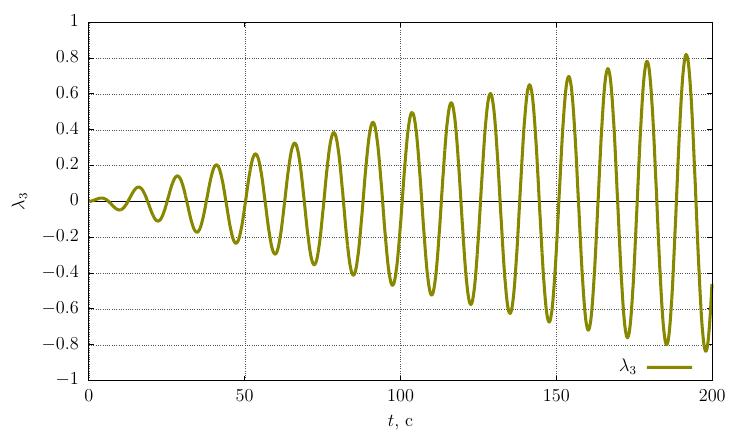
The projections of the angular velocity on its own axis

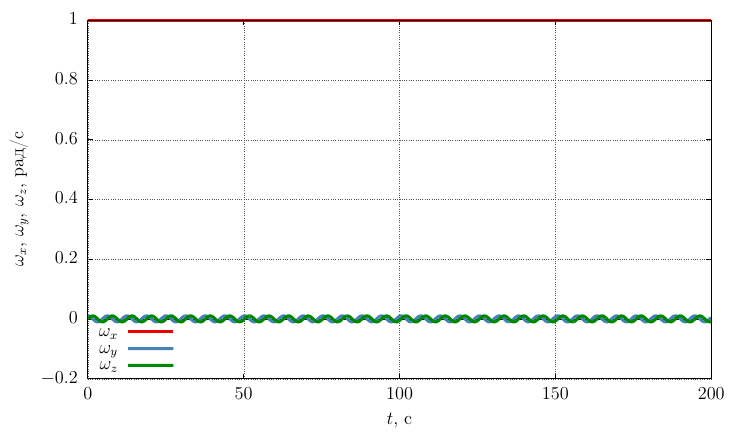
It is seen that with a sufficiently significant perturbation of the angular velocity, the motion remains stable rotation around the axis $x$ with a little precession.

A similar picture is observed for a body twisted around an axis with a minimum moment of inertia ( $I_x & lt; I_y = I_z$ ) $i_y = 1.5, \, i_z = 1.5, \, \ omega_0 = 1.0$ , glad / s $\ Delta \ omega_y = 1 \ cdot 10 ^ {- 2}$ , glad / s

Rodrigues-Hamilton orientation options

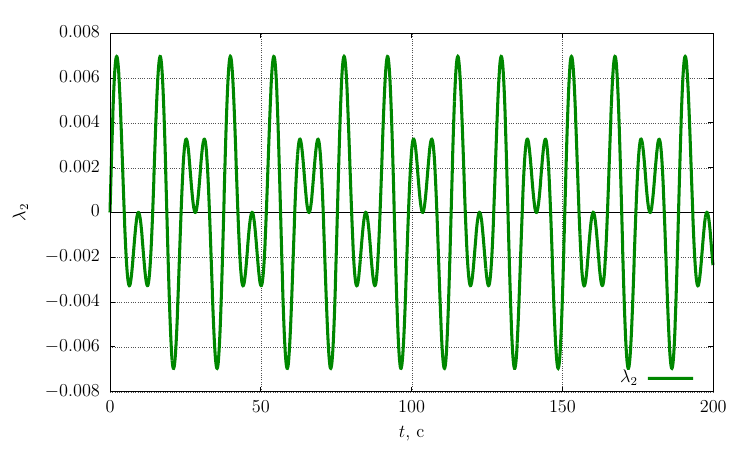
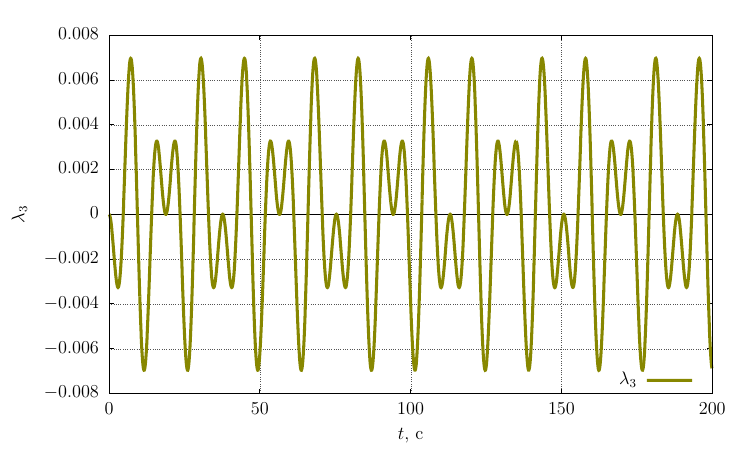
The projections of the angular velocity on its own axis

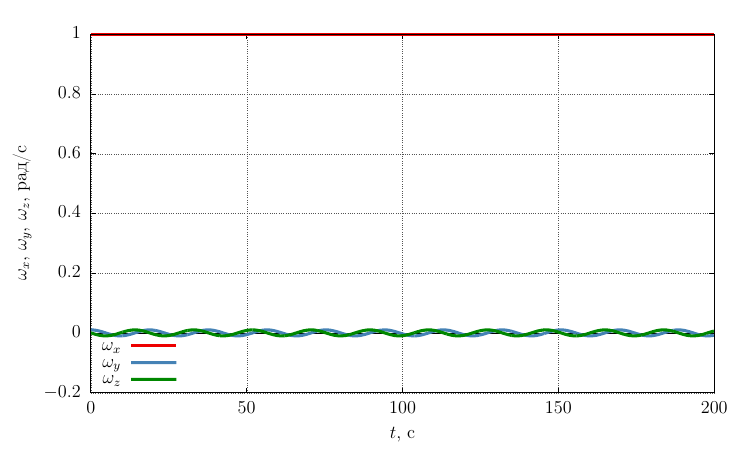
The precession frequency is significantly less than with a twist around an axis with a maximum moment of inertia, which is logical, since oscillations occur around an axis with a larger moment of inertia than in the case $I_x & gt; I_y = I_z$ .

Conclusion

All calculations were made by the author in SKA Maple 18. Charts are constructed from the calculation log with the Kile + LaTeX + gnuplot bundle.

I would also like to do the animation, but the author’s experience in this matter is extremely small. Therefore, I would like to ask a question to readers - is there software (for Linux / Windows), with which, having a set of values for orientation quaternion parameters depending on time, make an animated video illustrating body movement? I suspect that this can be done with Blender 3D, but not sure.

In the meantime, thank you for your attention!

Upd :

Thanks

However, I completely forgot to write that this article (and the previous one) was prepared using the Markdown & LaTeX Editor web application developed by the user parpalak . This system allows you to type texts of articles in Makdown and LaTeX and generates code suitable for direct insertion into the habra editor. I am grateful to the author for participating in the testing of the product. With his permission, I recommend this system for use in the preparation of mathematized texts of articles

To be continued…

Source: https://habr.com/ru/post/264381/

All Articles

Magic of tensor algebra: Part 18 - Mathematical modeling of the Janibekov effect

Content

Introduction

1. Differential equations of free motion in tensor form

2. The matrix form of the differential equations of motion of a rigid body in the Cartesian basis

3. Simulation of the Janibekov effect

Conclusion

Thanks

More articles: