Contingency tables and factorization of non-negative matrices
The factorization of non-negative matrices (NMF) is the representation of the matrix V as a product of the matrices W and H , in which all the elements of the three matrices are non-negative. This decomposition is used in various fields of knowledge, for example, in biology, computer vision, recommender systems. This publication will discuss the tables of the sociological and marketing data contingency, the factorization of which helps to understand the structure of the data in these tables.

Surprisingly, but on Habré, apparently, have not yet written about the NMF. The history of this method and general information are available on Wikipedia (eng) . But first, we will answer the question of why in general how to convert contingency tables.
')
If the number of rows and columns in the table is small, then a simple chart with columns or stacked bar graph is enough to have an idea of the table data. For example, a table obtained by intersecting the variables “gender” and “frequency of visiting sports or fitness clubs over the past month (4 categories)” of size 2x4 can be easily analyzed. Another thing, if the size of the table grows, say up to 20x30 or more. It will be impossible or extremely difficult to detect patterns in the jungle numbers of the table and in the forest of graph columns. In this case, the alternative is NMF, which lowers the dimension of the contingency table and displays the result in the form of heat maps. This gives a highly visual and easily interpretable view of the table.
Historically, one of the first methods of graphical representation of the structure of a transformed table is the analysis of correspondences (CA). It goes back to the principal component method, and is based on the singular matrix decomposition (SVD). About SVD can be read in this article on Habré. An excellent video with the definition of SVD and an example of building a correspondence analysis is also mentioned there. Matching analysis is a popular method, but factoring non-negative matrices, in my opinion, has several advantages. Considerations on this subject will be presented at the end of this article.
Further, only those definitions of factorization are given that are necessary for the analysis of contingency tables. Let table V be of size mxn . Denote by r the rank of matrices W and H , as a rule, r << min (n, m) . In contrast to the exact representation of the matrix in SVD, in the NMF we only have an approximate equality
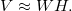
The matrices W and H are chosen in such a way as to minimize the loss function: D (V, WH) -> min. In our case, D is set on the basis of Kullback-Leibler divergence.
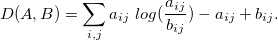
The question remains with the choice of rank r. There are several methods for estimating r (as, for example, in the case of the parameter k in the method k- average). But it is better to leave the question of choosing r to the discretion of the researcher / user, the rank at which the structure of the tables is most understandable, simple, relevant, and optimal.
In the environment of R there is a package nmf [1], in which several algorithms of factorization of non-negative matrices, decomposition visualization and its diagnostics are implemented. The capabilities of the NMF will be demonstrated on data from the 6th round of European Social Research (ESS) . In a previous publication , it was shown how you can load this data into R.
In the 2012 ESS project, 29 countries participated. The questionnaire, in particular, included 21 questions about the degree of importance of human values with a scale of six values: from “Very much like me” to “Not like me at all”. We transform each of these 21 single response variables into a logical variable. True value this variable takes for those respondents to whom this value is important - “Very much like me” and “Like me”; for all other respondents - doubters, for those who do not share this value or did not respond, the variable takes the value False.
We define the general population as "Men age 20-45 years." We build a table of intersections of these logical variables with each of the 29 countries of the study, taking into account the weights of the respondents. We get a table of size 29x21.
Notice that the contingency table is perceived in the extended sense; it contains a multiple response variable about human values. In addition, the size of the gene. aggregates in each country are different. Because of these two features of the table, it is important to normalize its rows to the size of a gene. sets of countries. That is, the table consists of weighted averages of the support values in each country of the ESS study. This is her fragment

Now we build the heat maps of the matrices W and H. They determine the decomposition of the studied characteristics in the space of 5 latent variables. The darker the cell, the more pronounced the correspondence between the latent variable and the value or country. I omit the mathematical details of the exact definition; details can be found in [1].
Next, we select only those human.values variables that are expressed only on one of the axes in this space. The names of the axes are given by me independently.

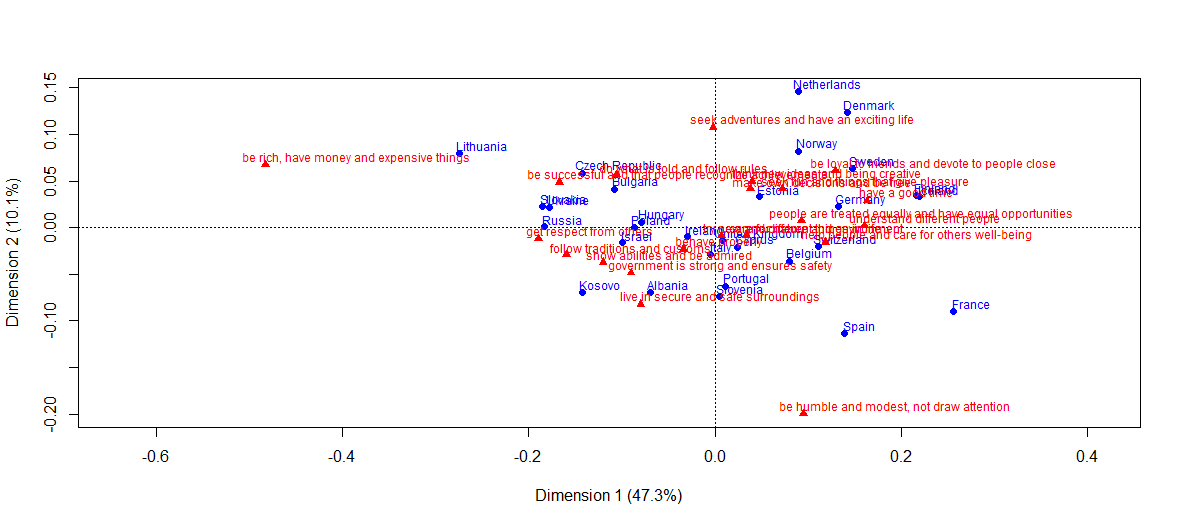
Below is the final result - the presentation of all 29 countries. Color expressed by the degree of compliance variables. In addition, countries are grouped following hierarchical clustering with a Euclidean metric in a 5-dimensional space of latent variables.
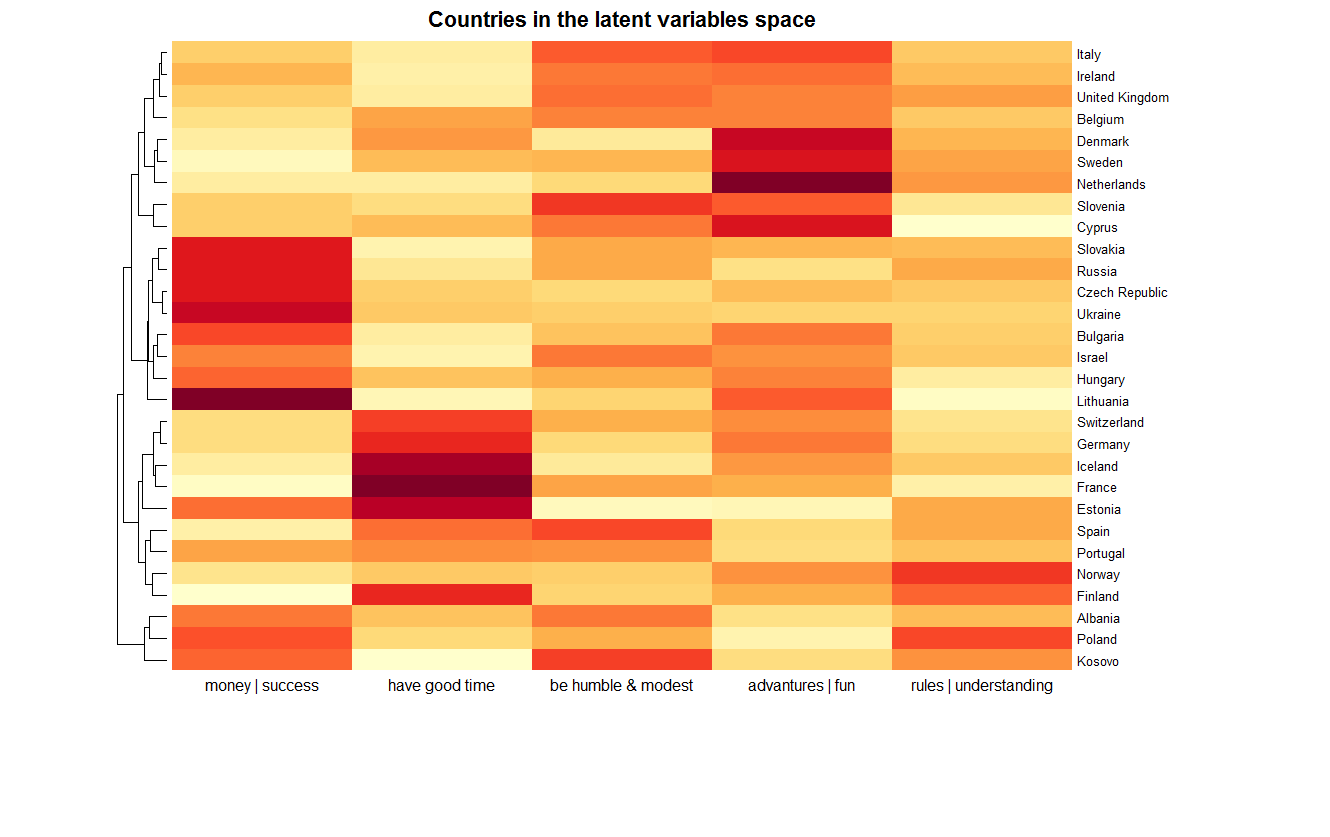
We see that in this space the closest country to Russia is Slovakia. These countries, in particular, are distinguished by expressiveness along the first axis, which cannot be said, for example, of France. In more detail this moment will be considered in the following part of article. The diagram also shows which countries make up the clusters, depending on the required details. For example, a cluster of Eastern European countries (Slovakia, Russia, Czech Republic, Ukraine, Bulgaria, Hungary, Lithuania) and Israel. Curious cluster from Albania, Kosovo and ... Poland. And Norway and Finland are quite far from Denmark and Sweden.
The use of NMF for a marketing contingency table can be found in this publication . It considers an example of the perception analysis of 14 car brands.
NMF diagrams, how good they would not be, in general, do not give grounds for making evidential conclusions about the similarities and differences of different countries regarding the concepts of values. This task will be considered in the next part of the article.
Literature:
[1] Renaud Gaujoux et al. A flexible R package for nonnegative matrix factorization. In: BMC Bioinformatics 11.1 (2010), p. 367.

Surprisingly, but on Habré, apparently, have not yet written about the NMF. The history of this method and general information are available on Wikipedia (eng) . But first, we will answer the question of why in general how to convert contingency tables.
')
If the number of rows and columns in the table is small, then a simple chart with columns or stacked bar graph is enough to have an idea of the table data. For example, a table obtained by intersecting the variables “gender” and “frequency of visiting sports or fitness clubs over the past month (4 categories)” of size 2x4 can be easily analyzed. Another thing, if the size of the table grows, say up to 20x30 or more. It will be impossible or extremely difficult to detect patterns in the jungle numbers of the table and in the forest of graph columns. In this case, the alternative is NMF, which lowers the dimension of the contingency table and displays the result in the form of heat maps. This gives a highly visual and easily interpretable view of the table.
Historically, one of the first methods of graphical representation of the structure of a transformed table is the analysis of correspondences (CA). It goes back to the principal component method, and is based on the singular matrix decomposition (SVD). About SVD can be read in this article on Habré. An excellent video with the definition of SVD and an example of building a correspondence analysis is also mentioned there. Matching analysis is a popular method, but factoring non-negative matrices, in my opinion, has several advantages. Considerations on this subject will be presented at the end of this article.
Further, only those definitions of factorization are given that are necessary for the analysis of contingency tables. Let table V be of size mxn . Denote by r the rank of matrices W and H , as a rule, r << min (n, m) . In contrast to the exact representation of the matrix in SVD, in the NMF we only have an approximate equality
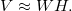
The matrices W and H are chosen in such a way as to minimize the loss function: D (V, WH) -> min. In our case, D is set on the basis of Kullback-Leibler divergence.
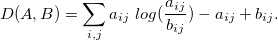
The question remains with the choice of rank r. There are several methods for estimating r (as, for example, in the case of the parameter k in the method k- average). But it is better to leave the question of choosing r to the discretion of the researcher / user, the rank at which the structure of the tables is most understandable, simple, relevant, and optimal.
In the environment of R there is a package nmf [1], in which several algorithms of factorization of non-negative matrices, decomposition visualization and its diagnostics are implemented. The capabilities of the NMF will be demonstrated on data from the 6th round of European Social Research (ESS) . In a previous publication , it was shown how you can load this data into R.
In the 2012 ESS project, 29 countries participated. The questionnaire, in particular, included 21 questions about the degree of importance of human values with a scale of six values: from “Very much like me” to “Not like me at all”. We transform each of these 21 single response variables into a logical variable. True value this variable takes for those respondents to whom this value is important - “Very much like me” and “Like me”; for all other respondents - doubters, for those who do not share this value or did not respond, the variable takes the value False.
We define the general population as "Men age 20-45 years." We build a table of intersections of these logical variables with each of the 29 countries of the study, taking into account the weights of the respondents. We get a table of size 29x21.
Notice that the contingency table is perceived in the extended sense; it contains a multiple response variable about human values. In addition, the size of the gene. aggregates in each country are different. Because of these two features of the table, it is important to normalize its rows to the size of a gene. sets of countries. That is, the table consists of weighted averages of the support values in each country of the ESS study. This is her fragment

The code for building the table and finding its factorization rank 5.
These studies have already been loaded, the names of the objects remained unchanged.
We list the variable names in the database of the study relevant questions about human values.
Add to the database logical variables converted to numeric type and multiplied by the weights of the respondents
Build the required table (denoted by cntry.human.values)
And we perform factorization of non-negative matrices of rank 5
We list the variable names in the database of the study relevant questions about human values.
human.values <- c("ipcrtiv", "imprich", "ipeqopt", "ipshabt", "impsafe", "impdiff", "ipfrule", "ipudrst", "ipmodst", "ipgdtim", "impfree", "iphlppl", "ipsuces", "ipstrgv", "ipadvnt", "ipbhprp", "iprspot", "iplylfr", "impenv", "imptrad", "impfun") Add to the database logical variables converted to numeric type and multiplied by the weights of the respondents
weighted.human.values<-paste(human.values,"w",sep="_") add.binary.human.values<-function(){ adding.variables<-paste("srv.data[,c('", paste(weighted.human.values, collapse = "','"), "'):=list(", paste("as.numeric(",human.values, " %in% c( 'Very much like me', 'Like me' )) *dweight", collapse = ", " ), ")]", sep="") eval(parse(text=adding.variables)) return(T) } add.binary.human.values() Build the required table (denoted by cntry.human.values)
target.audience.data <- srv.data[gndr == 'Male' & agea >= 25 & agea<=40, c(weighted.human.values,'dweight', 'cntry'), with=FALSE] cntry.human.values <- t(sapply(unique(target.audience.data[,cntry]), function(x) colSums(target.audience.data[J(x)][,weighted.human.values,with=FALSE]))) cntry.pop.sizes <- target.audience.data[,list(W.Total=sum(dweight)),by=cntry] cntry.human.values <- cntry.human.values/cntry.pop.sizes[,W.Total]*100 rownames(cntry.human.values) <- c("Albania", "Belgium", "Bulgaria", "Switzerland", "Cyprus", "Czech Republic", "Germany", "Denmark", "Estonia", "Spain", "Finland", "France", "United Kingdom", "Hungary", "Ireland", "Israel", "Iceland", "Italy", "Lithuania", "Netherlands", "Norway", "Poland", "Portugal", "Russia", "Sweden", "Slovenia", "Slovakia", "Ukraine", "Kosovo") colnames(cntry.human.values) <- sub(srv.variables[J(human.values)][,title], pattern = "Important to |Important that ", replacement = "") And we perform factorization of non-negative matrices of rank 5
nmf.fit <- nmf(cntry.human.values, 5, method = "brunet", seed=123456, nrun=100) Now we build the heat maps of the matrices W and H. They determine the decomposition of the studied characteristics in the space of 5 latent variables. The darker the cell, the more pronounced the correspondence between the latent variable and the value or country. I omit the mathematical details of the exact definition; details can be found in [1].
Next, we select only those human.values variables that are expressed only on one of the axes in this space. The names of the axes are given by me independently.
Profile mapping
nmf.selected <- nmf.fit[, c(2, 7:10, 13, 15, 21)] basismap(t(nmf.selected), tracks=NA, main="Latent variables: Profiles explanation", scale = "r1", legend = NA, Rowv=TRUE, labCol = c("money | success", "have good time", "be humble & modest", "advantures | fun", "rules | understanding")) 
Below is the final result - the presentation of all 29 countries. Color expressed by the degree of compliance variables. In addition, countries are grouped following hierarchical clustering with a Euclidean metric in a 5-dimensional space of latent variables.
Hidden text
basismap (nmf.selected, tracks = NA, main = "Countries in the latent variables space",
legend = NA, labCol = c ("money | success", "have good time", "be humble & modest",
«Advantures | fun ”,“ rules | understanding ”))
legend = NA, labCol = c ("money | success", "have good time", "be humble & modest",
«Advantures | fun ”,“ rules | understanding ”))

We see that in this space the closest country to Russia is Slovakia. These countries, in particular, are distinguished by expressiveness along the first axis, which cannot be said, for example, of France. In more detail this moment will be considered in the following part of article. The diagram also shows which countries make up the clusters, depending on the required details. For example, a cluster of Eastern European countries (Slovakia, Russia, Czech Republic, Ukraine, Bulgaria, Hungary, Lithuania) and Israel. Curious cluster from Albania, Kosovo and ... Poland. And Norway and Finland are quite far from Denmark and Sweden.
Comparison with matching results
What are the advantages of NMF?
- Unlike NMF, in the graphical representation of the classical correspondence analysis, only two eigenvalues are used (in the graph above, the cumulative inertia of the CA axes is 57.4%). In NMF, visualization is visual and for a rank greater than two.
- Secondly, the heat maps provide information in a more structured and clear way than the CA plane.
library(ca) plot(ca(cntry.human.values), what=c("all", "active")) 
What are the advantages of NMF?
- Unlike NMF, in the graphical representation of the classical correspondence analysis, only two eigenvalues are used (in the graph above, the cumulative inertia of the CA axes is 57.4%). In NMF, visualization is visual and for a rank greater than two.
- Secondly, the heat maps provide information in a more structured and clear way than the CA plane.
The use of NMF for a marketing contingency table can be found in this publication . It considers an example of the perception analysis of 14 car brands.
NMF diagrams, how good they would not be, in general, do not give grounds for making evidential conclusions about the similarities and differences of different countries regarding the concepts of values. This task will be considered in the next part of the article.
Literature:
[1] Renaud Gaujoux et al. A flexible R package for nonnegative matrix factorization. In: BMC Bioinformatics 11.1 (2010), p. 367.
Source: https://habr.com/ru/post/264375/
All Articles