How to find out the year of release of the song on the set of audio characteristics?
The Scalable Machine Learning course on Apache Spark recently completed, covering the use of MLlib for machine learning. The course consisted of video lectures and practical tasks. Laboratory work needed to be done at PySpark, and since I’d more often come across scala in my work, I decided to resolve the main labs in this language, and at the same time learn the material better. Of course, there are no big differences. Basically, this is what PySpark actively uses NumPy , and in the version with scala Breeze is used.
The first two workshops covered the study of the basic operations of linear algebra in NumPy and familiarity with the apache spark, respectively. Actually machine learning began with the third laboratory work, it is disassembled below.
This laboratory work is aimed at studying the linear regression method (one of the teaching methods with the teacher). We will use part of the data from the Million Song Dataset . Our goal is to find the best model that predicts the year of a song based on a set of audio characteristics using the linear regression method.
This laboratory work includes the following steps:
1. Reading, parsing and data processing
2. Creating and evaluating the base model
3. Implementation of the basic linear regression algorithm, training and model evaluation
4. Finding a model using MLlib, setting up hyper parameters
5. Add dependencies between characteristics
')
Raw data is currently stored in a text file and consists of lines of this type:
Each line starts with a label (year of release of the song), and then the audio characteristics of the recording are separated by a comma.
The first thing we start with is: present the data in the form of RDD:
Let's see how many records we have:
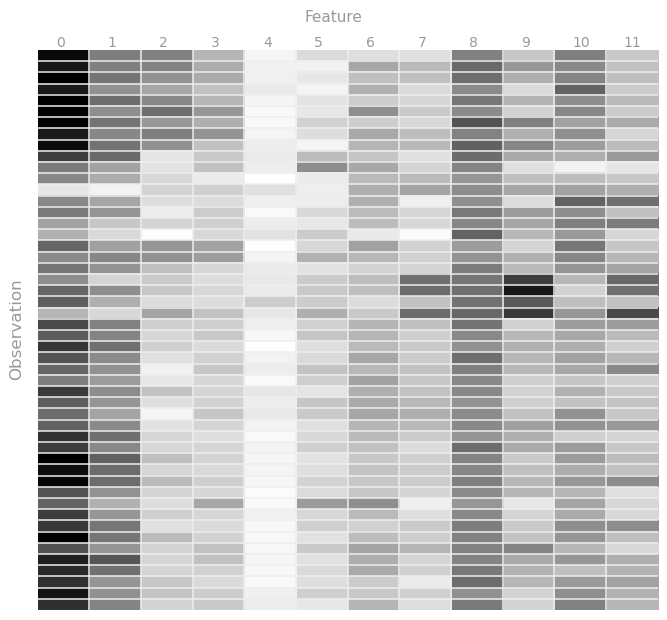
To better understand the data provided to us, let's visualize them by building a heat map for at least some of the observations. Since characteristics range from 0 to 1, then let the closer the value is to one, the darker the shade of gray will be, and vice versa.
In MLlib, a training sample (more precisely, its elements) should be stored in a special LabeledPoint object, which consists of a label (label) and a set of characteristics (features) belonging to this label. In our case, the label will be the year, and the characteristics will be the audio data of the recording.
We write a function that, at the input, will receive one line from our data set and return the finished labeledPoint.
Let's translate our data into a working version:
Now let's examine the labels and find the range of years in which our data fit; To do this, you need to find the maximum and minimum year.
As we can see, the labels are located between 1922 and 2011. In learning tasks, it is often natural to shift the values so that they start from scratch. Let's create a new RDD that will contain objects with labels offset by 1922.0.
We have almost finished preparing the data, and all we have to do is split the data into 3 subsets:
For this purpose, spark has a randomSplit method:
Let's try to come up with a simple model with which we could compare the accuracy of the models obtained in the future. In the simplest case, the model can predict the average value of the year, regardless of the incoming data. Let's calculate this value:
To evaluate how well our model works, let's use the square root of the root-mean-square error ( RMSE ) as an estimate
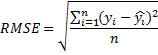 .
.
In our case, y i is the label-year, and y i with a cap is the year predicted by the model. First, we implement a function that calculates the square of the difference between the label and prediction and the function that will calculate the RMSE:
Now we can calculate the RMSE of our data based on the predictions of the base model. To do this, we prepare new RDD containing tuples with observed and forecast years.
Note that each RMSE received can be interpreted as an average prediction error for a given set (in terms of number of years)
Now that we have a base model and its evaluation, we can check whether the linear regression method can offer us a better result than the previous one.
Recall the gradient descent step formula for linear regression:
w i + 1 = w i - α i * ∑ (w i T * x j - y j ) * x j .
Where i is the iteration number and j is the observation ID.
First, let's implement a function that calculates the term for this update (w T * x - y) * x:
Go ahead: we need to implement a function that will take the calculated weights of the model and the observed values, and give the tuple (the observed value, the predicted value).
It’s time to implement the Gradient descent method:
Well, everything is ready! It now remains to train our linear regression model on the entire training sample and evaluate its accuracy on a test sample:
At each iteration, we considered the RMSE for the training sample and now we can track how the algorithm behaved: for this we construct two graphs. The first is the logarithm of the error from the iteration number for all 50 iterations, and the second is the actual error value for the last 44 iterations.

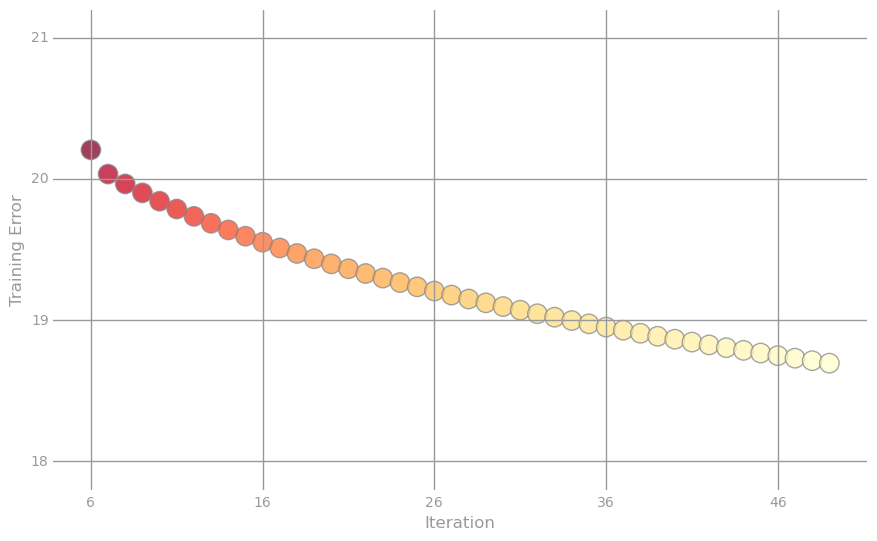
We clearly achieved improvements: now our predictions are wrong, on average, not by 21 years, but only by 18. It should be noted that if the number of iterations is increased to 500, then the error will be 16,403.
Well, now it looks much better. However, let's see if we can improve the situation using the free term (constant, intercept) and regularization. To do this, we will use the ready-made class LinearRegressionWithSGD, which essentially implements the same algorithm as we implemented, but more efficiently, with various additional functionality, such as stochastic gradient descent, the ability to add a free member, as well as L1 and L2 regularization.
To begin with, we will implement a function that will help configure the model:
We used RidgeRegressionWithSGD, because this is a wrapper with an already specified type of L2 regularization, just as we could use LinearRegressionWithSGD, but then we would have to add one more line
Run the algorithm:
The result is comparable to our implementation (and if we recall that with an equal number of iterations, we got 16.4, then the result is not so good), but we can probably improve the result by trying different values of the regularization. Let's see what happens if the regularization parameter is taken 1e-10, 1e-5 and 1.
It remains to check how the model behaves if you change the step value (alpha) and the number of iterations. We will take the regularization parameter for the one that gave the best value, let the step be 1e-5, 10, and the number of iterations 500 and 5.
So, we can conclude that with a small step, the algorithm very slowly approaches the minimum, and with a large one it diverges altogether, and very quickly.
So far, we have used only those characteristics that were provided to us. For example, if we only had 2 x 1 and x 2 characteristics, then the model would be:
w 0 + w 1 x 1 + w 2 x 2 .
However, nothing prevents us from creating additional characteristics: returning to our example, we could come up with a more complex model:
w 0 + w 1 x 1 + w 2 x 2 + w 3 x 1 x 2 + w 4 x 2 x 1 + w 5 x 1 2 + w 6 x 2 2
Let's do it; for this we need to implement a function that would multiply in pairs the values of the characteristics and return a new set combined with the original one.
Now let's create a new model, for this we need to apply the function described above to our datasets:
Well, then we must repeat the search for hyper parameters for the new model, since the settings found earlier may not give the best result. But we will not repeat this here, but we will immediately substitute the optimal ones.
And finally, let's evaluate our new model on test data. Please note that we did not use test data to select the best model. Therefore, our estimate gives an unbiased estimate of how the resulting model will work on new data. Now we can see how the new model is better than the base one.
Well, that's all, the final assessment certainly does not look particularly good, but definitely better than the one we started with.
The first two workshops covered the study of the basic operations of linear algebra in NumPy and familiarity with the apache spark, respectively. Actually machine learning began with the third laboratory work, it is disassembled below.
This laboratory work is aimed at studying the linear regression method (one of the teaching methods with the teacher). We will use part of the data from the Million Song Dataset . Our goal is to find the best model that predicts the year of a song based on a set of audio characteristics using the linear regression method.
This laboratory work includes the following steps:
1. Reading, parsing and data processing
2. Creating and evaluating the base model
3. Implementation of the basic linear regression algorithm, training and model evaluation
4. Finding a model using MLlib, setting up hyper parameters
5. Add dependencies between characteristics
')
1. Reading, parsing and data processing
Raw data is currently stored in a text file and consists of lines of this type:
2001.0,0.884123733793,0.610454259079,0.600498416968,0.474669212493,0.247232680947,0.357306088914,0.344136412234,0.339641227335,0.600858840135,0.425704689024,0.60491501652,0.419193351817 Each line starts with a label (year of release of the song), and then the audio characteristics of the recording are separated by a comma.
The first thing we start with is: present the data in the form of RDD:
val sc = new SparkContext("local[*]", "week3") val rawData: RDD[String] = sc.textFile("millionsong.txt") Let's see how many records we have:
val numPoints = rawData.count() println(numPoints) > 6724 To better understand the data provided to us, let's visualize them by building a heat map for at least some of the observations. Since characteristics range from 0 to 1, then let the closer the value is to one, the darker the shade of gray will be, and vice versa.

In MLlib, a training sample (more precisely, its elements) should be stored in a special LabeledPoint object, which consists of a label (label) and a set of characteristics (features) belonging to this label. In our case, the label will be the year, and the characteristics will be the audio data of the recording.
We write a function that, at the input, will receive one line from our data set and return the finished labeledPoint.
import org.apache.spark.mllib.regression.LabeledPoint import org.apache.spark.mllib.linalg.Vectors def parsePoint(line: String) = { val sp = line.split(',') LabeledPoint(sp.head.toDouble, Vectors.dense(sp.tail.map(_.toDouble))) } Let's translate our data into a working version:
val parsedDataInit: RDD[LabeledPoint] = rawData.map(parsePoint) Now let's examine the labels and find the range of years in which our data fit; To do this, you need to find the maximum and minimum year.
val onlyLabels = parsedDataInit.map(_.label) val minYear = onlyLabels.min() val maxYear = onlyLabels.max() println(s"max: $maxYear, min: $minYear") > max: 2011.0, min: 1922.0 As we can see, the labels are located between 1922 and 2011. In learning tasks, it is often natural to shift the values so that they start from scratch. Let's create a new RDD that will contain objects with labels offset by 1922.0.
val parsedData = parsedDataInit.map(x => LabeledPoint(x.label - minYear, x.features)) We have almost finished preparing the data, and all we have to do is split the data into 3 subsets:
- training sample - it is on it that we will train our model
- test sample - on this data we will check how well the trained model predicts the result
- test sample - this set will simulate new data and help us truthfully evaluate the best model
For this purpose, spark has a randomSplit method:
val weights = Array(0.8, 0.1, 0.1) val seed = 42 val splitData: Array[RDD[LabeledPoint]] = parsedData.randomSplit(weights, seed).map(_.cache()) val parsedTrainData = splitData(0) val parsedValData = splitData(1) val parsedTestData = splitData(2) val nTrain = parsedTrainData.count() val nVal = parsedValData.count() val nTest = parsedTestData.count() println(nTrain, nVal, nTest, nTrain + nVal + nTest) println(parsedData.count()) >(5402,622,700,6724) > 6724 2. Creating and evaluating the base model
Let's try to come up with a simple model with which we could compare the accuracy of the models obtained in the future. In the simplest case, the model can predict the average value of the year, regardless of the incoming data. Let's calculate this value:
val averageTrainYear = parsedTrainData.map(_.label).mean() println(averageTrainYear) > 53.68659755646054 To evaluate how well our model works, let's use the square root of the root-mean-square error ( RMSE ) as an estimate
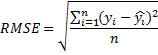 .
.In our case, y i is the label-year, and y i with a cap is the year predicted by the model. First, we implement a function that calculates the square of the difference between the label and prediction and the function that will calculate the RMSE:
def squaredError(label: Double, prediction: Double) = math.pow(label - prediction, 2) def calcRMSE(labelsAndPreds: RDD[(Double, Double)]) = math.sqrt(labelsAndPreds.map(x => squaredError(x._1, x._2)).sum() / labelsAndPreds.count()) Now we can calculate the RMSE of our data based on the predictions of the base model. To do this, we prepare new RDD containing tuples with observed and forecast years.
val labelsAndPredsTrain = parsedTrainData.map(x => x.label -> averageTrainYear) val rmseTrainBase = calcRMSE(labelsAndPredsTrain) val labelsAndPredsVal = parsedValData.map(x => x.label -> averageTrainYear) val rmseValBase = calcRMSE(labelsAndPredsVal) val labelsAndPredsTest = parsedTestData.map(x => x.label -> averageTrainYear) val rmseTestBase = calcRMSE(labelsAndPredsTest) > Base model: Baseline Train RMSE = 21,496 Baseline Validation RMSE = 21,100 Baseline Test RMSE = 21,100 Note that each RMSE received can be interpreted as an average prediction error for a given set (in terms of number of years)
3. Implementation of the basic linear regression algorithm, training and model evaluation
Now that we have a base model and its evaluation, we can check whether the linear regression method can offer us a better result than the previous one.
Recall the gradient descent step formula for linear regression:
w i + 1 = w i - α i * ∑ (w i T * x j - y j ) * x j .
Where i is the iteration number and j is the observation ID.
First, let's implement a function that calculates the term for this update (w T * x - y) * x:
import breeze.linalg.{ DenseVector => BreezeDenseVector } def gradientSummand(weights: BreezeDenseVector[Double], lp: LabeledPoint): BreezeDenseVector[Double] = { val x = BreezeDenseVector(lp.features.toArray) val y = lp.label val wx: Double = weights.t * x (wx - y) * x } Go ahead: we need to implement a function that will take the calculated weights of the model and the observed values, and give the tuple (the observed value, the predicted value).
def getLabeledPrediction(weights: BreezeDenseVector[Double], observation: LabeledPoint): (Double, Double) = { val x = BreezeDenseVector(observation.features.toArray) val y = observation.label val prediction: Double = weights.t * x (y, prediction) } It’s time to implement the Gradient descent method:
def linregGradientDescent(trainData: RDD[LabeledPoint], numIters: Int) = { // val n = trainData.count() // - val d = trainData.first().features.size // ( d ) val w = BreezeDenseVector.zeros[Double](d) val alpha = 1.0 val errorTrain = BreezeDenseVector.zeros[Double](numIters) for (i <- 0 until numIters) { val labelsAndPredsTrain = trainData.map(x => getLabeledPrediction(w, x)) errorTrain(i) = calcRMSE(labelsAndPredsTrain) val gradient: BreezeDenseVector[Double] = trainData.map(x => gradientSummand(w, x)).reduce((dv1, dv2) => dv1 + dv2) val alpha_i = alpha / ( n * math.sqrt(i+1) ) w -= alpha_i * gradient } (w, errorTrain) } Well, everything is ready! It now remains to train our linear regression model on the entire training sample and evaluate its accuracy on a test sample:
val numIters = 50 val (weightsCustom, errorTrainCustom) = linregGradientDescent(parsedTrainData, numIters = numIters) val labelsAndPreds = parsedValData.map(lp => getLabeledPrediction(weightsCustom, lp)) val rmseValLRCustom = calcRMSE(labelsAndPreds) > Custom Linear regression algorithm Weights = DenseVector(22.429559050840954, 20.57848949803509, -0.38069311013701224, 8.286892767462648, 5.725188813272974, -4.547779089973534, 15.494323154076804, 3.7888305696294986, 10.205862111138764, 5.877745123091225, 11.13061973187094, 3.6849419014146703) Baseline = 21,100 CustomLR = 18,341 At each iteration, we considered the RMSE for the training sample and now we can track how the algorithm behaved: for this we construct two graphs. The first is the logarithm of the error from the iteration number for all 50 iterations, and the second is the actual error value for the last 44 iterations.


We clearly achieved improvements: now our predictions are wrong, on average, not by 21 years, but only by 18. It should be noted that if the number of iterations is increased to 500, then the error will be 16,403.
4. Finding a model using MLlib, setting up hyper parameters
Well, now it looks much better. However, let's see if we can improve the situation using the free term (constant, intercept) and regularization. To do this, we will use the ready-made class LinearRegressionWithSGD, which essentially implements the same algorithm as we implemented, but more efficiently, with various additional functionality, such as stochastic gradient descent, the ability to add a free member, as well as L1 and L2 regularization.
To begin with, we will implement a function that will help configure the model:
import org.apache.spark.mllib.regression.RidgeRegressionWithSGD def tuneModel(numIterations: Int = 500, stepSize: Double = 1.0, regParam: Double = 1e-1) = { val model = new RidgeRegressionWithSGD() model.optimizer .setStepSize(stepSize) .setNumIterations(numIterations) .setRegParam(regParam) model.setIntercept(true) } We used RidgeRegressionWithSGD, because this is a wrapper with an already specified type of L2 regularization, just as we could use LinearRegressionWithSGD, but then we would have to add one more line
model.optimizer.setUpdater(new SquaredL2Updater)Run the algorithm:
val ridgeModel = tuneModel(numIterations = 500, stepSize = 1.0, regParam = 1e-1).run(parsedTrainData) val weightsRidge = ridgeModel.weights val interceptRidge = ridgeModel.intercept val rmseValRidge = calcError(ridgeModel, parsedValData) > RidgeRegressionWithSGD weights = [16.49707401343799,15.090143596016913,-0.33882414671890876,6.21399054657087,3.9399959912276765,-3.326873353072514,11.219894673155363,2.605614334247694,7.368594539065305,4.352602095699236,7.936294197372791,2.597979499976716] intercept = 13.40151357030002 > RidgeRegressionWithSGD validation RMSE Baseline = 21,100 CustomLR = 18,341 RidgeLR = 18,924 The result is comparable to our implementation (and if we recall that with an equal number of iterations, we got 16.4, then the result is not so good), but we can probably improve the result by trying different values of the regularization. Let's see what happens if the regularization parameter is taken 1e-10, 1e-5 and 1.
var bestRMSE = rmseValRidge var bestRegParam = 1.0 var bestModel = ridgeModel for (regParam <- Array(1e-10, 1e-5, 1)) { val model = tuneModel(regParam = regParam).run(parsedTrainData) val rmseVal = calcError(model, parsedValData) println(f"regParam = $regParam%.0e, RMSE = $rmseVal%.3f") if (rmseVal < bestRMSE) { bestRMSE = rmseVal bestRegParam = regParam bestModel = model } } > regParam = 1e-10, RMSE = 16,292 regParam = 1e-05, RMSE = 16,292 regParam = 1e+00, RMSE = 23,179 > Best model weights = [29.417184432817606,31.186800575308965,-17.37215928935944,8.288971260120093,5.111705048981693,-22.61199371516979,25.231243109503467,-4.989933439427709,6.709806469376133,-0.08589332350175394,9.958713420381914,-6.252319073419468] intercept = 16.170147238736043 regParam = 1.0E-10 > Grid validation RMSE Baseline = 21,100 LR0 = 18,341 LR1 = 18,924 LRGrid = 16,292 It remains to check how the model behaves if you change the step value (alpha) and the number of iterations. We will take the regularization parameter for the one that gave the best value, let the step be 1e-5, 10, and the number of iterations 500 and 5.
for (alpha <- Array(1e-5, 10)) { for (numIter <- Array(5, 500)) { val model = tuneModel(numIterations = numIter, stepSize = alpha, regParam = bestRegParam).run(parsedTrainData) val rmseVal = calcError(model, parsedValData) println(f"alpha = $alpha%.0e, numIters = $numIter, RMSE = $rmseVal%.3f") } } > alpha = 1e-05, numIters = 5, RMSE = 56,912 alpha = 1e-05, numIters = 500, RMSE = 56,835 alpha = 1e+01, numIters = 5, RMSE = 351471078,741 alpha = 1e+01, numIters = 500, RMSE = 3696615731186115000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000,000 So, we can conclude that with a small step, the algorithm very slowly approaches the minimum, and with a large one it diverges altogether, and very quickly.
5. Add dependencies between characteristics
So far, we have used only those characteristics that were provided to us. For example, if we only had 2 x 1 and x 2 characteristics, then the model would be:
w 0 + w 1 x 1 + w 2 x 2 .
However, nothing prevents us from creating additional characteristics: returning to our example, we could come up with a more complex model:
w 0 + w 1 x 1 + w 2 x 2 + w 3 x 1 x 2 + w 4 x 2 x 1 + w 5 x 1 2 + w 6 x 2 2
Let's do it; for this we need to implement a function that would multiply in pairs the values of the characteristics and return a new set combined with the original one.
def twoWayInteractions(lp: LabeledPoint) = { val features: List[Double] = lp.features.toArray.toList val two = (for (x <- features; y <- features) yield (x,y)).map(x => x._1 * x._2) val inter = two ::: features LabeledPoint(lp.label, Vectors.dense(inter.toArray)) } Now let's create a new model, for this we need to apply the function described above to our datasets:
val trainDataInteract = parsedTrainData.map(twoWayInteractions) val valDataInteract = parsedValData.map(twoWayInteractions) val testDataInteract = parsedTestData.map(twoWayInteractions) Well, then we must repeat the search for hyper parameters for the new model, since the settings found earlier may not give the best result. But we will not repeat this here, but we will immediately substitute the optimal ones.
val modelInteract = tuneModel(regParam = bestRegParam).run(trainDataInteract) val rmseValLRInteract = calcError(modelInteract, valDataInteract) > Interact validation RMSE Baseline = 21,100 LR0 = 18,341 LR1 = 18,924 LRGrid = 16,292 LRInteract = 15,225 And finally, let's evaluate our new model on test data. Please note that we did not use test data to select the best model. Therefore, our estimate gives an unbiased estimate of how the resulting model will work on new data. Now we can see how the new model is better than the base one.
> Test validation RMSE Baseline = 21,100 LRInteract = 15,905 Well, that's all, the final assessment certainly does not look particularly good, but definitely better than the one we started with.
Source: https://habr.com/ru/post/264193/
All Articles