Open Data Analysis in R, Part 1

Introduction

At the time of this writing, most applications based on open data (on official data.mos.ru/apps and data.gov.ru ) are interactive guides on the infrastructure of a city or settlement with visual visualization and often with the option of choosing the best route. The purpose of this and subsequent publications is to draw the attention of the community to the discussion of strategies for analyzing open data, including aimed at forecasting, building statistical models and extracting information not presented explicitly. The toolkit uses the R language and the RStudio development environment.

As an illustration of the ease of use of R, we consider a small example and visualize on a map the register of the attraction of the Criminal Code, Homeowners Association for 2013 in Ulyanovsk . This data set contains information about the fines of various management companies. For visualization, the number of oral remarks, the number of fines and fines in rubles for all time presented in dataset were selected. This data (as well as all others from open sources that I came across) tends to have a lot of omissions, typos, etc. therefore, pre-processed data is loaded into R:

ulyanovsk.data <- read.csv('./data/formated_tsj.csv')


For visualization, an interface to google maps and the ggplot2 library are used; for organizing graphs on an output device, use gridExtra:
')

In dataset there are lat and lon columns, which contain information about latitude and longitude. We need a map not of the whole Ulyanovsk but only its parts, the coordinates of which are in the sample:


Apply to the map penalties in rubles (column penalties_rub_total):


The number of fines in units:


Number of oral remarks in pieces:


Building it all together:

grid.arrange(p0, p1, p2, p3, ncol=2)




The size of the point and the value of red monotonously increase with the parameter (for example, the more penalties, the more and red the point). The graphs show that in the surveyed dataset, management companies from the right bank of Ulyanovsk have more fines and comments than from the left bank.

Research statistics crash

This section uses data from a single interdepartmental information and statistical system . Dataset contains the death rate from traffic accidents per 100 thousand people by regions of the Russian Federation for 2011-2014:





Average for each year by regions:

apply(accidents[,2:5],2,FUN = mean)


## y2011 y2012 y2013 y2014
## 21.36942 21.55694 20.18582 20.34727

Histograms:





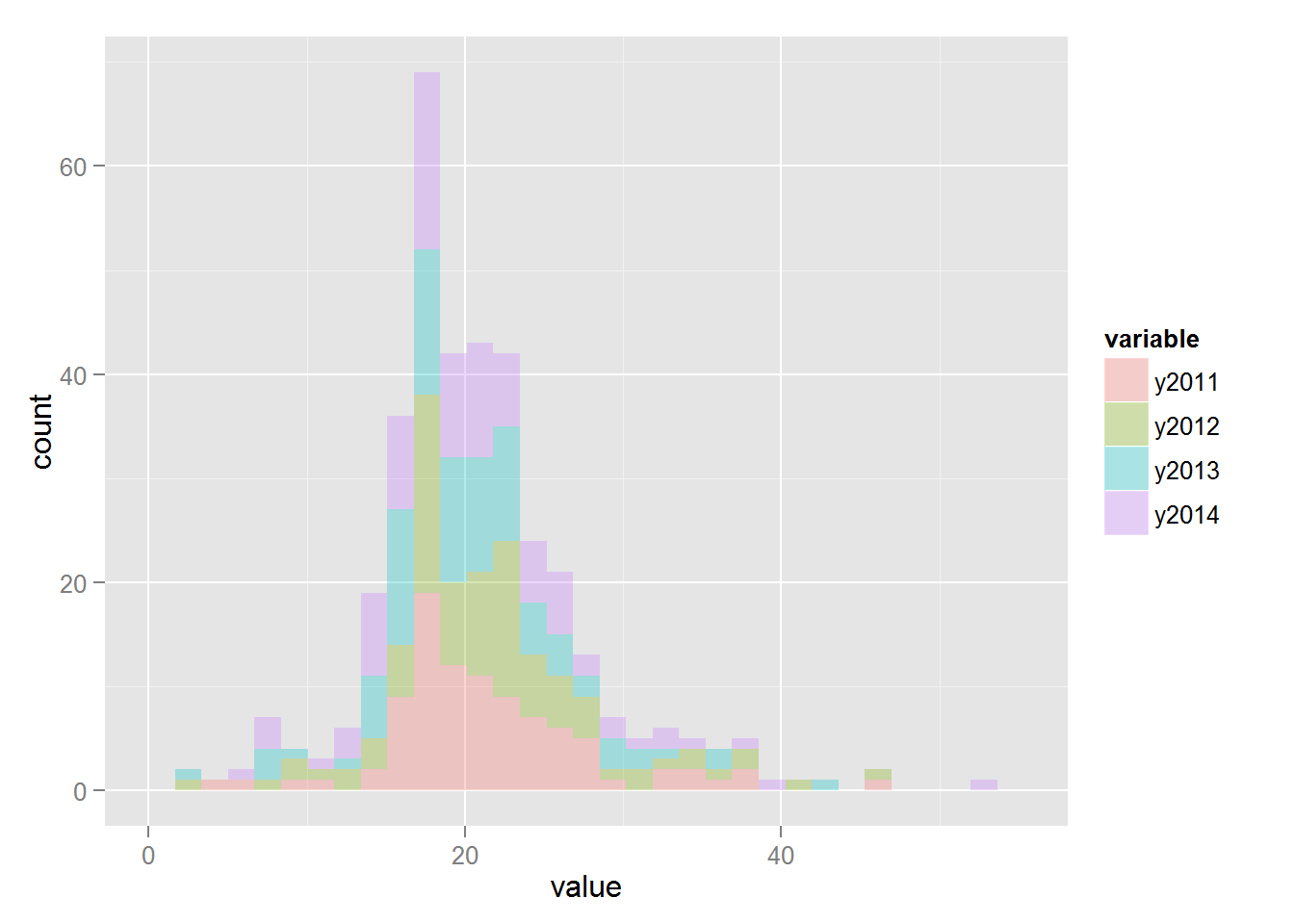
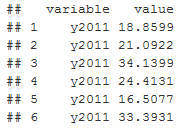
The melt function reorganizes datasets in such a way that the value column stores the value of the indicator, in the variable column the year for which the indicator was obtained:

head(accidents.melt)




It is interesting to compare whether the difference in indicators for different years is statistically significant. The following model assumptions are accepted:

1) The value of the indicator is a random variable obeying the student's distribution
2) Each year has its own distribution parameters, nu is the normality parameter, sigma is the variance, mu is the average
3) The parameters nu, sigma, mu are also random variables with their own year-independent distributions.

Formal statement of the problem: using data to establish whether the distribution parameter mu is different for different years. If we write out the Bayes formula for our case (which I will not give here, in order not to overload the article), then we get a hierarchical model:

1) death rate (field value in accidents.melt) ~ t (mu, sigma, nu)
2) mu | group_id ~ N (mu_hyp, sigma_hyp)
3) sigma | group_id ~ Unif (a_hyp, b_hyp | group_id)
4) nu | group_id ~ Exp (lambda_hyp)

Where mu | group_id ~ N (mu_hyp, sigma_hyp) indicates that the mu parameter for the group_id group has a normal distribution with hyper parameters mu_hyp, sigma_hyp.
The variable group_id takes a value depending on the year, 1 for 2011, 2 for 2012, etc .:

accidents.melt$group_id <- as.numeric(accidents.melt$variable)


For modeling, R uses an interface to the Jags language and the auxiliary function plotPost from the file DBDA2E-utilities.R, which can be found here (by John Kruschke):



The description of the model takes place in the jags language, therefore, first a file or a string variable is created inside R with the model:



After the model is specified, it is passed to the jags along with the data:



Jags uses MCMC and implements a random walk model in our parameter space mu, sigma, nu. Moreover, the probability that the parameters will take a specific value is proportional to their joint probability, although the joint probability is not considered explicitly. Thus, jags returns a list of mu, sigma, nu values, so you can estimate their probabilities using histograms. The following lines launch our model and return the result:



To answer our question about the value of the mu parameter for different years, we consider histograms of the difference between the values ​​of the parameters:










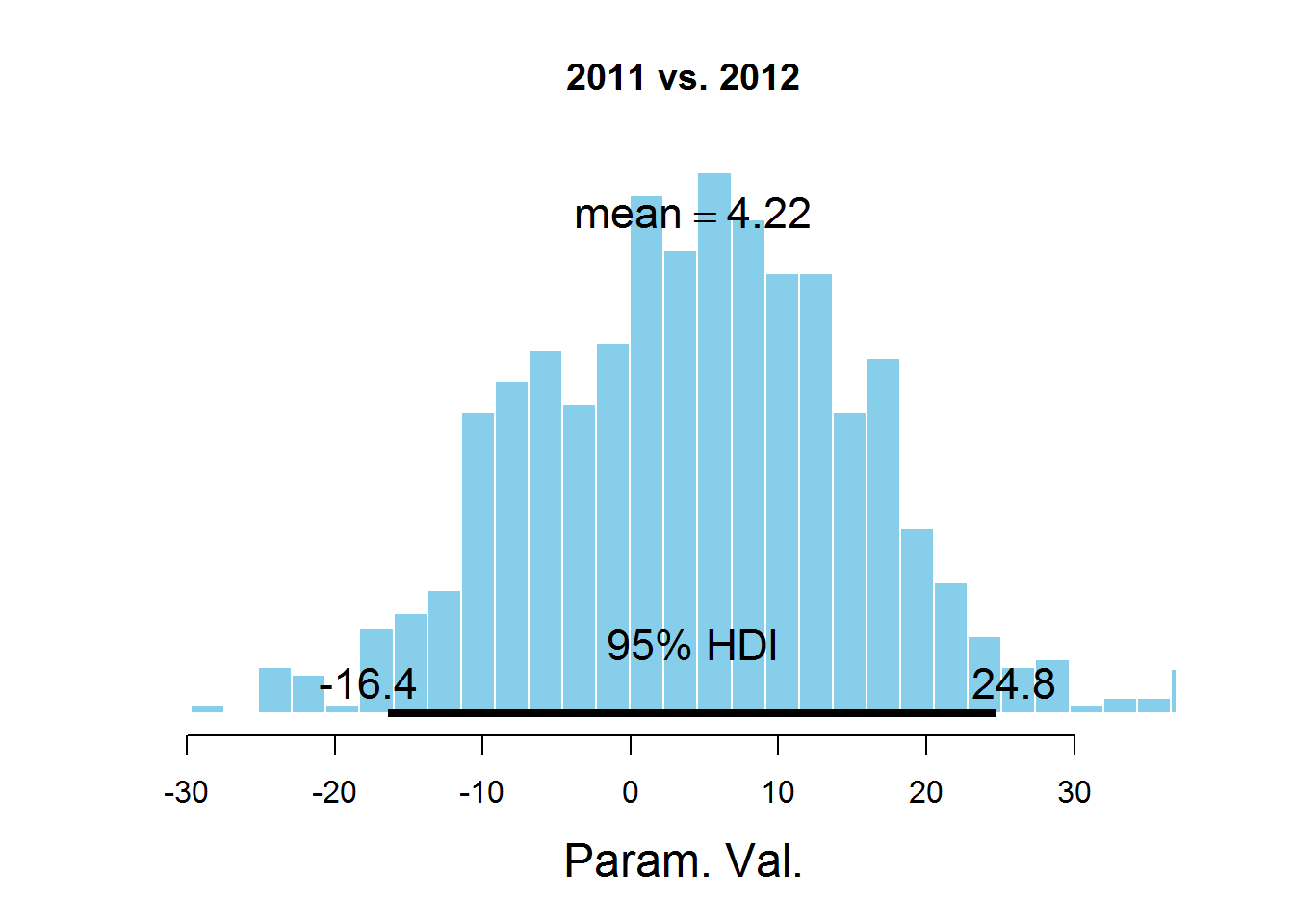
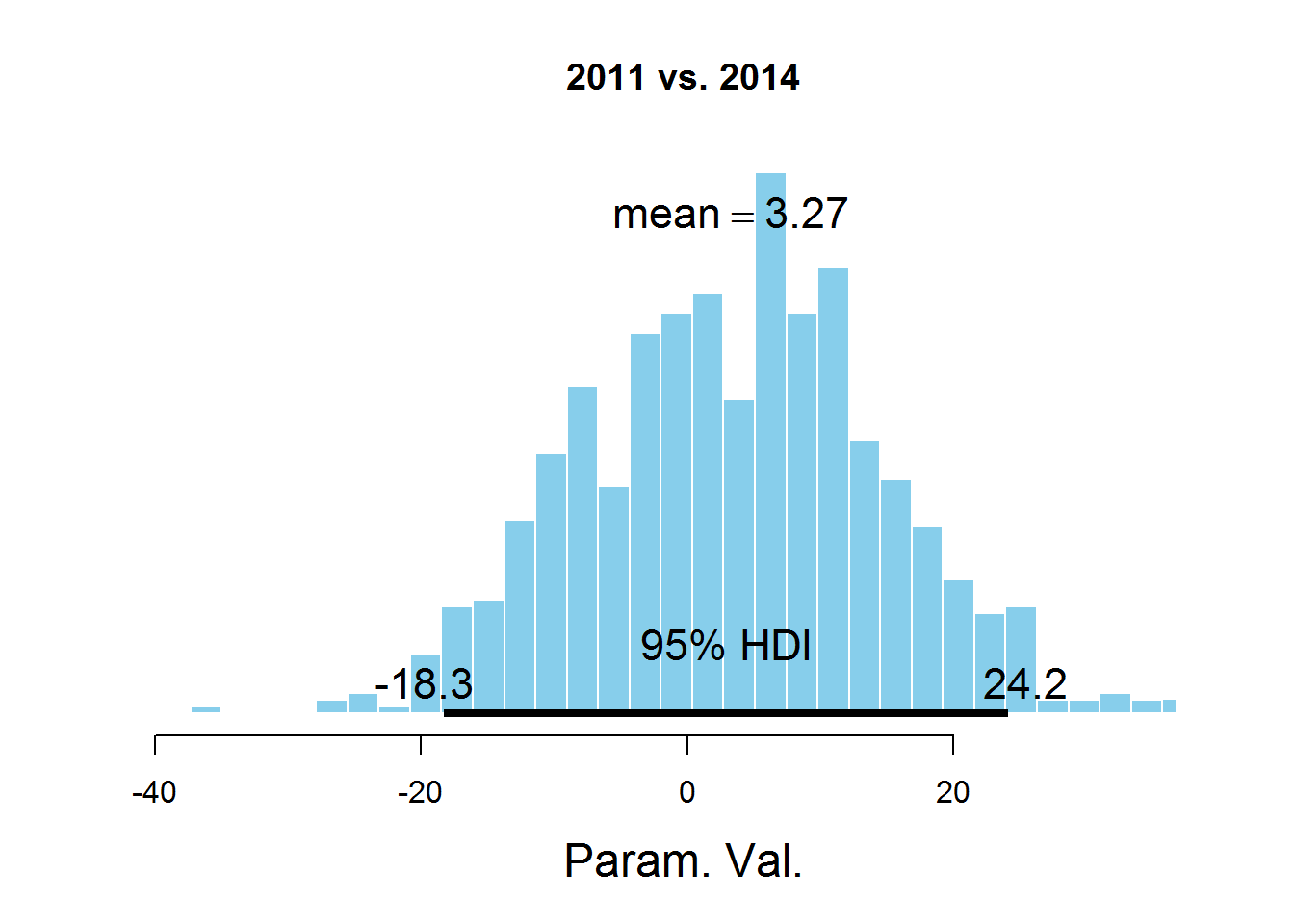
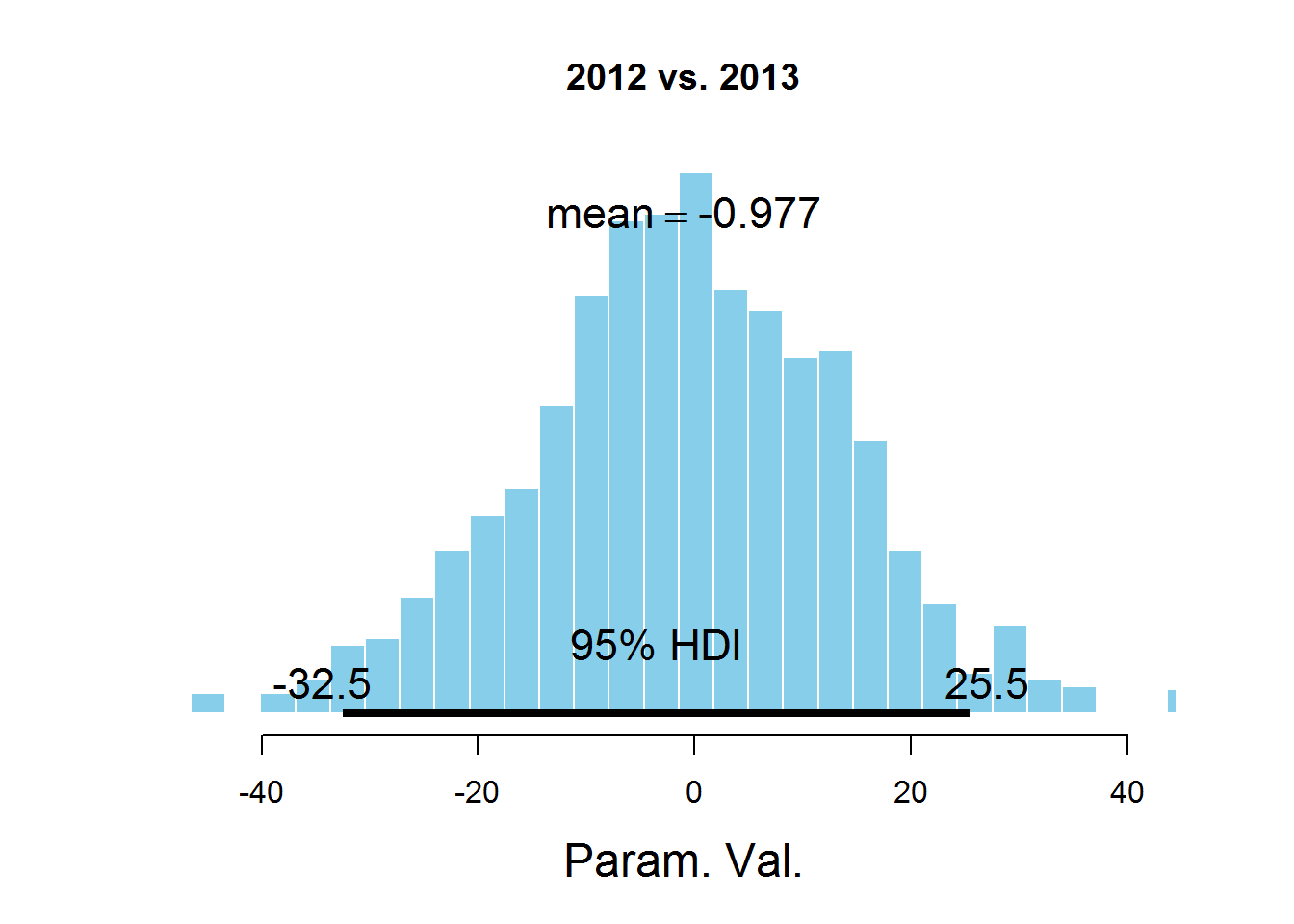
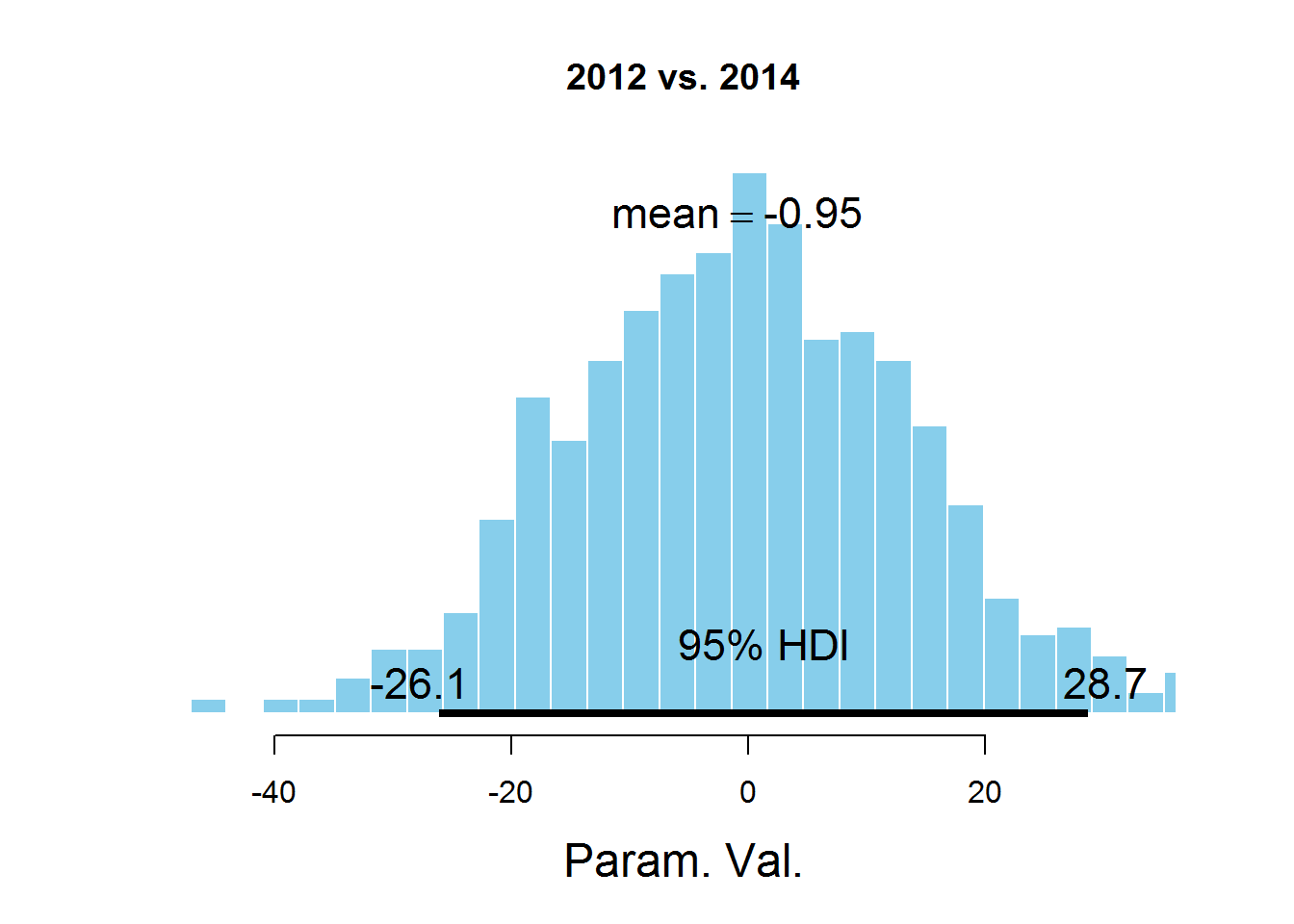
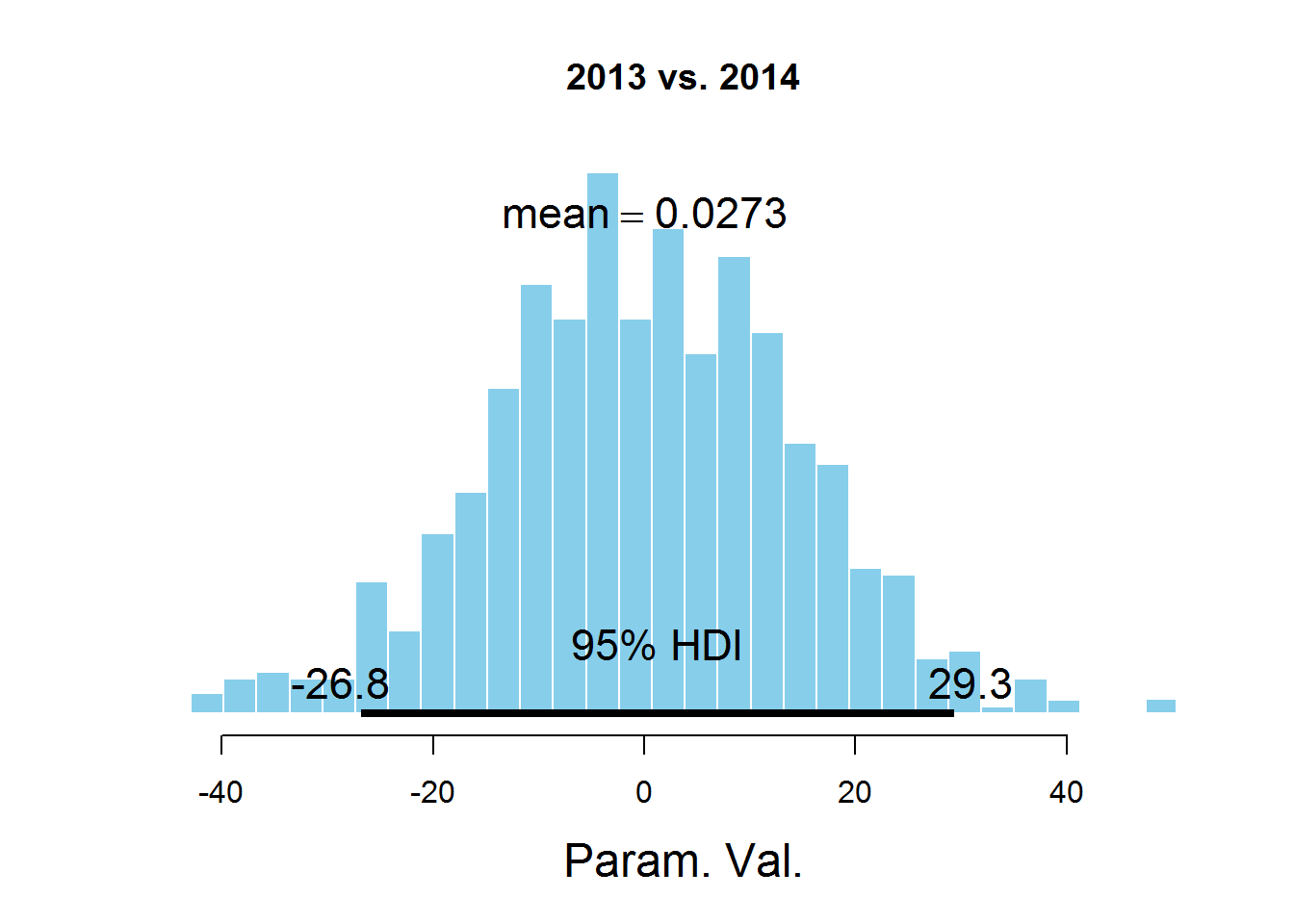
The graphs indicate the HDI interval, the values ​​in which have a greater probability than the values ​​outside the interval, and the sum of the probabilities of these values ​​is 0.95. It can be seen that the value 0 falls in HDI, which suggests that the mu parameter is the same for all the years represented in the dataset. There is a controversial point here - the HDI value is selected according to the knowledge of the subject area, i.e. perhaps for this task a value of 95% is not the most suitable.