The magic of tensor algebra: Part 17 - Sketch of nut Janibekova
This article is dedicated to the blessed memory of my teacher, Doctor of Technical Sciences, Professor Alexander N. Kabelkov, founder and first dean of the Faculty of Physics and Mathematics of the South Russian State Technical University (NPI)
This video illustrates a repeated experiment - instead of “lamb” some self-made nonsense is used.
')
It happened in 1985, at the Salyut-7 orbital station, during a visit by its crew of the Soyuz T-13 spacecraft, composed of astronauts Dzhanibekov V.A. and Savinykh V.P. I will not describe in my own words, quoting one of multiple network sources
I think that for the seed this is enough. In fact, there is nothing extraordinary in the “Janibekov effect” (although he is credited with a possible change of the Earth’s poles every 12,000 years, and other global cataclysms). Using the apparatus of tensor algebra and the theory of stability of mechanical motion, we will try to understand what happens to the mysterious nut.
The figure shows the object of our study. Surely every reader has seen such a nut at least once in their life. I can not vouch for the similarity with the original, the artist from me is still, but nonetheless.
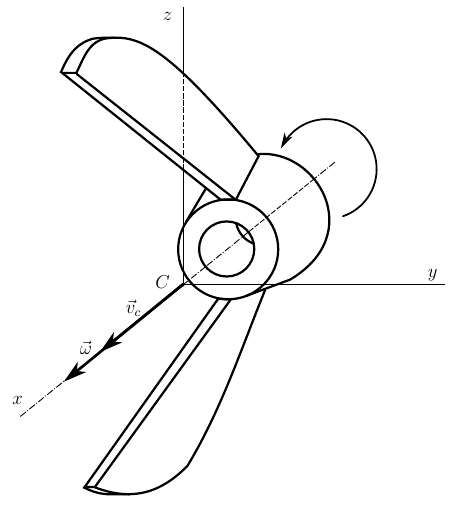
Firstly, we will study the movement of the nut (for now, although there is a simulation in the plans) qualitatively. Therefore, we will not be interested in the specific dimensions of this product. The shape of this nut is important to us, from which we, practically calculating nothing, can draw some conclusions.
The nut makes a free movement, so it is convenient to choose its center of mass as a pole. In addition, let the own coordinate system (associated with the body) be Cartesian, and let its axes coincide with the main axes of inertia. Such axes can always be found, and they will be orthogonal, as we strictly argued in the previous article . So we can assume that the central inertia tensor of the nut will be represented by a diagonal matrix
)

Obviously, the greatest major axial moment of inertia will be - the nut has the longest form in the plane perpendicular to the axis
- the nut has the longest form in the plane perpendicular to the axis  . About moments of inertia
. About moments of inertia  and
and  one can argue - it all depends on the ratio of the thickness of the central part to its diameter and the distance of the center of mass from the threaded hole, but let us assume that the shape of the nut is such that
one can argue - it all depends on the ratio of the thickness of the central part to its diameter and the distance of the center of mass from the threaded hole, but let us assume that the shape of the nut is such that  . Then we introduce the dimensionless moments of inertia.
. Then we introduce the dimensionless moments of inertia.
)

and since
)

In this case, the central inertia tensor takes the form
)

Since the nut moves as a free body after the thread is removed, the form of writing the equations of motion is obvious
)
%20%3D%20%5Csum%20%5Cvec%20M_%7Bc%7D(%5Cvec%20F_k%5E%7B%5C%2Ce%7D)%20%0A%5Cend%7Balign*%7D%20%0A)
Since the nut moves in a non-inertial reference system, which freely falls to Earth (spacecraft cabin, weightlessness), assuming the insignificance of air resistance and neglecting other perturbations, we will consider the right parts of system (5) to be zero
)
%20%3D%200%0A%5Cend%7Balign*%7D%20%0A)
Taking into account the initial conditions, the equation of motion of the pole is easily integrated, and we get uniform and rectilinear motion of the center of mass. All the salt in the second equation, which is also easy to integrate, because its left side is an absolute derivative of the moment of the nut movement relative to the center of mass
%20%3D%20%5Cfrac%7B%5Ctilde%20d%5Cvec%20L_c%7D%7Bdt%7D%20%2B%20%5Cvec%5Comega%20%5Ctimes%20%5Cvec%20L_c%20%3D%20%5Cfrac%7Bd%5Cvec%20L_c%7D%7Bdt%7D%0A)
Where - the local derivative of the MCD, taken in a related coordinate system, and the formula itself is called the Boer formula .
- the local derivative of the MCD, taken in a related coordinate system, and the formula itself is called the Boer formula .
Thus, the second equation gives the integral

which speaks of the immutability of the MKD. Considering that at the beginning the angular velocity is directed strictly along the axis MCD will also be directed along the same axis, because the asymmetry of the body in this case will have no effect, the MCD will have a projection on the axis
MCD will also be directed along the same axis, because the asymmetry of the body in this case will have no effect, the MCD will have a projection on the axis  and it will be equal
and it will be equal  . Where does the evolution described in the experience of Janibekov come from?
. Where does the evolution described in the experience of Janibekov come from?
Suppose that under the action of a short small perturbation, the angular velocity of the nut deviated from the law, which is given by equation (6) by a small value . Then the angular velocity of the nut will be equal to
. Then the angular velocity of the nut will be equal to
)

Rewrite the second equation (6) in the tensor form

and substitute there (7)
)
%20%2B%20%5Cvarepsilon%5E%7B%5C%2Crkm%7D%20%5C%2C%20%5Cleft(%5Comega_%7B%5C%2Ck%7D%20%2B%20%5CDelta%20%5Comega_%7B%5C%2Ck%7D%5Cright)%20%5C%2C%20g_%7B%5C%2Cms%7D%20%5C%2C%20I_%7B%5C%2Cp%7D%5E%7B%5C%2Cs%7D%20%5C%2C%20%5Cleft(%5Comega%5E%7B%5C%2Cp%7D%20%2B%20%5CDelta%20%5Comega%5E%7B%5C%2Cp%7D%5Cright)%20%3D%200%0A)
We open in (8) brackets
)

But, that corresponds to the steady state of motion. The last term (9) is rejected as a small 2nd order, reducing equation (9) to the form
that corresponds to the steady state of motion. The last term (9) is rejected as a small 2nd order, reducing equation (9) to the form

Recalculate the components of the angular velocity formulas
)

Substitute (10) into (9) and factor out the common factors
%20%5C%2C%20%5CDelta%5Comega%5E%7B%5C%2Cl%7D%20%3D%200%0A)
Using the properties of the Kronecker delta and omitting the indices of the inertia tensor, we obtain
%20%5C%2C%20%5CDelta%5Comega%5E%7B%5C%2Cl%7D%20%3D%200%0A)
or
)

Where) - rank tensor
- rank tensor ) .
.
The resulting system of equations (11) is called the linearized system of equations of perturbed motion and serves to study the stability of steady-state motion in the first approximation.
Pay attention, using the tensors, we completely forgot that there is a terrible matrix multiplication in equation (6) and a vector product. Another illustration of the power of the tensor approach to the transformation of vector-matrix forms.
Let us turn again to the matrix form in equation (11), allowing it relative to the derivative of the angular velocity deviations
)

The first Lyapunov method, which we will use to assess the stability of the movement of the nut, involves the study of the eigenvalues of the matrix . In order for steady motion to be stable, the eigenvalues (of which there will be three) of the matrix
. In order for steady motion to be stable, the eigenvalues (of which there will be three) of the matrix  must have negative real parts.
must have negative real parts.
However, first we need to get the matrix whose elements satisfy the tensor relation
whose elements satisfy the tensor relation
)
%0A)
To begin with, we recall that we work in Cartesian coordinates, which means the metric tensor is represented by the unit matrix, the Levi-Civita tensor is the Weblen symbols, which we have already mentioned, and the inertia tensor) coincides with the rank inertia tensor
coincides with the rank inertia tensor ) .
.
For convolution of expression (13), one can use SKA, but since I have not yet figured out component-wise work with tensors in Maxima and Maple, I quickly sketched the following code in Maple using its linear algebra tools
Passing the original data through Maple, we get a matrix at the output
%20%5C%5C%0A0%20%26%26%20%5Comega%20%5C%2C%20I_x%20%5C%2C%20%5Cleft(i_y%20-%201%5Cright)%20%26%26%200%0A%5Cend%7Bbmatrix%7D%0A)
Where - the angular velocity of rotation of the nut immediately after the descent from the thread on the steady-state part of the movement, before the roll. This angular velocity can be considered constant.
- the angular velocity of rotation of the nut immediately after the descent from the thread on the steady-state part of the movement, before the roll. This angular velocity can be considered constant.
It is easy to get the matrix

The characteristic equation for calculating the eigenvalues of this matrix is
(1%20-%20i_z)%7D%7Bi_y%20%5C%2C%20i_z%7D%20%5C%2C%20%5Clambda%20%3D%200%0A)
Solving it we get own numbers
)
(1%20-%20i_z)%7D%7Bi_y%20%5C%2C%20i_z%7D%7D%2C%20%5Cquad%20%5C%2C%20%5Clambda_3%20%3D%20-%5Comega%20%5C%2C%20%5Csqrt%7B%5Cfrac%7B(i_y%20-%201)(1%20-%20i_z)%7D%7Bi_y%20%5C%2C%20i_z%7D%7D%0A)
Eigenvalues take real values if the dimensionless moments of inertia satisfy the condition
)

Otherwise, two proper numbers will be purely imaginary. If we build graphs of eigenvalues and
and  from the dimensionless moments of inertia, then we will see that if the condition (15) is violated, the graphs fail in the complex area.
from the dimensionless moments of inertia, then we will see that if the condition (15) is violated, the graphs fail in the complex area.
Positive root of characteristic polynomial

Negative root of characteristic polynomial
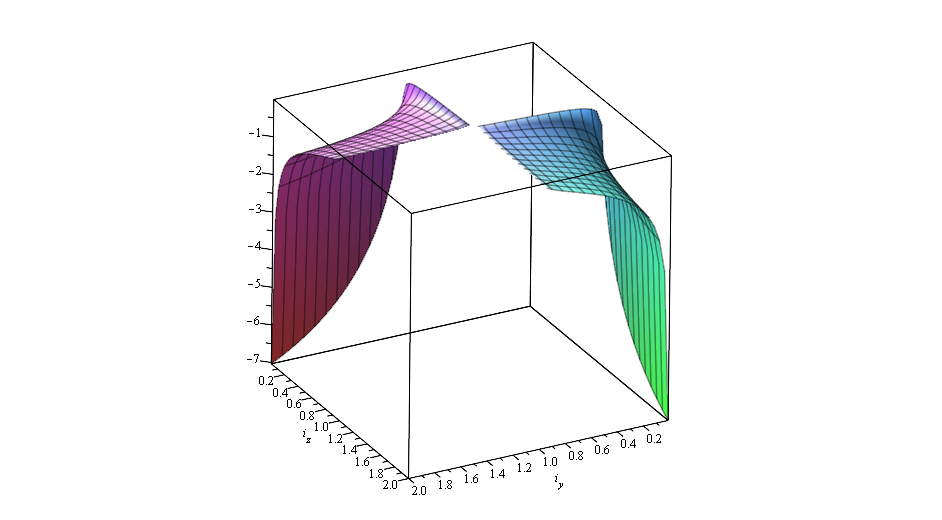
At least one eigenvalue with a positive real part speaks of the instability of the steady state of motion.
Now let's see, because condition (15) satisfies condition (3) that we adopted at the beginning. When the ratio between the moments of inertia, when

that is, being initially twisted around an axis with an intermediate between the maximum and minimum value of the moment of inertia, the nut behaves unstably, performs a revolution, and then again tries to find a stable position, and again performs a revolution. It is known that stable rotations of a free body are possible only around axes with maximum and minimum inertia moments.
If a
)

then we get the purely imaginary roots of the characteristic equation, and the first Lyapunov method does not unambiguously answer the question whether the motion will be stable in this case. But based on what the mechanics do not know today and on the oscillatory nature of solving linear equations with imaginary roots of the characteristic equation, one can assume periodic oscillations of the angular velocity vector around the steady state, which corresponds to the processes of precession and nutation.
In this regard, our planet, satisfying condition (16) will not experience the effect of Janibekov. So the global catastrophe with the change of poles does not threaten us.
This article was some warm-up. Perhaps we will come back to the “lamb nut”, but for now - thank my readers for their attention!
> To be continued ...
Introduction
This video illustrates a repeated experiment - instead of “lamb” some self-made nonsense is used.
')
It happened in 1985, at the Salyut-7 orbital station, during a visit by its crew of the Soyuz T-13 spacecraft, composed of astronauts Dzhanibekov V.A. and Savinykh V.P. I will not describe in my own words, quoting one of multiple network sources
When the astronauts unpacked the cargo delivered to orbit, they had to unscrew the so-called "lambs" - nuts and ears. It is necessary to hit the ear of the "lamb", and he spins himself. Then, unwinding to the end and jumping off the threaded rod, the nut continues, rotating, to fly by inertia in weightlessness (approximately like a flying rotating propeller). So, Vladimir Aleksandrovich noticed that having flown about 40 centimeters ears forward, the nut suddenly makes a sudden 180-degree turn and continues to fly in the same direction, but already with ears back and spinning in the other direction. Then, again flying 40 centimeters, the nut again makes a 180-degree roll and continues to fly forward again, like the first time, and so on. Janibekov repeatedly repeated the experiment, and the result was invariably repeated. In general, a rotating nut, flying in zero gravity, makes sharp 180-degree periodic coups every 43 centimeters. He also tried to use other objects instead of a nut, for example, a plasticine ball with a conventional nut stuck to it, which, having flown some distance, made the same sudden coups.
I think that for the seed this is enough. In fact, there is nothing extraordinary in the “Janibekov effect” (although he is credited with a possible change of the Earth’s poles every 12,000 years, and other global cataclysms). Using the apparatus of tensor algebra and the theory of stability of mechanical motion, we will try to understand what happens to the mysterious nut.
1. Nut "lamb" - mass-inertial characteristics
The figure shows the object of our study. Surely every reader has seen such a nut at least once in their life. I can not vouch for the similarity with the original, the artist from me is still, but nonetheless.

Firstly, we will study the movement of the nut (for now, although there is a simulation in the plans) qualitatively. Therefore, we will not be interested in the specific dimensions of this product. The shape of this nut is important to us, from which we, practically calculating nothing, can draw some conclusions.
The nut makes a free movement, so it is convenient to choose its center of mass as a pole. In addition, let the own coordinate system (associated with the body) be Cartesian, and let its axes coincide with the main axes of inertia. Such axes can always be found, and they will be orthogonal, as we strictly argued in the previous article . So we can assume that the central inertia tensor of the nut will be represented by a diagonal matrix
Obviously, the greatest major axial moment of inertia will be
and since
In this case, the central inertia tensor takes the form
2. Differential equations of steady motion of the nut
Since the nut moves as a free body after the thread is removed, the form of writing the equations of motion is obvious
Since the nut moves in a non-inertial reference system, which freely falls to Earth (spacecraft cabin, weightlessness), assuming the insignificance of air resistance and neglecting other perturbations, we will consider the right parts of system (5) to be zero
Taking into account the initial conditions, the equation of motion of the pole is easily integrated, and we get uniform and rectilinear motion of the center of mass. All the salt in the second equation, which is also easy to integrate, because its left side is an absolute derivative of the moment of the nut movement relative to the center of mass
Where
Thus, the second equation gives the integral
which speaks of the immutability of the MKD. Considering that at the beginning the angular velocity is directed strictly along the axis
3. Differential equations of the perturbed motion of the nut
Suppose that under the action of a short small perturbation, the angular velocity of the nut deviated from the law, which is given by equation (6) by a small value
Rewrite the second equation (6) in the tensor form
and substitute there (7)
We open in (8) brackets
But,
Recalculate the components of the angular velocity formulas
Substitute (10) into (9) and factor out the common factors
Using the properties of the Kronecker delta and omitting the indices of the inertia tensor, we obtain
or
Where
The resulting system of equations (11) is called the linearized system of equations of perturbed motion and serves to study the stability of steady-state motion in the first approximation.
Pay attention, using the tensors, we completely forgot that there is a terrible matrix multiplication in equation (6) and a vector product. Another illustration of the power of the tensor approach to the transformation of vector-matrix forms.
4. The study of the stability of the movement of the nut Dzhanibekov on the first approximation (the first Lyapunov method)
Let us turn again to the matrix form in equation (11), allowing it relative to the derivative of the angular velocity deviations
The first Lyapunov method, which we will use to assess the stability of the movement of the nut, involves the study of the eigenvalues of the matrix
However, first we need to get the matrix
To begin with, we recall that we work in Cartesian coordinates, which means the metric tensor is represented by the unit matrix, the Levi-Civita tensor is the Weblen symbols, which we have already mentioned, and the inertia tensor
For convolution of expression (13), one can use SKA, but since I have not yet figured out component-wise work with tensors in Maxima and Maple, I quickly sketched the following code in Maple using its linear algebra tools
restart; with(LinearAlgebra): # - levi_civita := proc(i, j, k) local E := IdentityMatrix(3,3); local A := Matrix(3, 3); local i1 := 0; A[1] := E[i]; A[2] := E[j]; A[3] := E[k]; return Determinant(Transpose(A)); end proc: # J := Matrix( [ [I[xx], 0, 0], [0, a*I[xx], 0], [0, 0, b*I[xx]] ]); g := IdentityMatrix(3, 3); Omega := Vector([omega, 0, 0]); L := J . Omega; # G G := Matrix(3, 3); for r from 1 to 3 do for l from 1 to 3 do G[r, l] := 0; for k from 1 to 3 do summ := 0; for m from 1 to 3 do summ := summ + levi_civita(r, k, m)*Omega[k]*J[m, l] + levi_civita(r,k,m)*g[k,l]*L[m]; end do: G[r, l] := G[r, l] + summ; end do: end do: end do: Passing the original data through Maple, we get a matrix at the output
Where
It is easy to get the matrix
The characteristic equation for calculating the eigenvalues of this matrix is
Solving it we get own numbers
Eigenvalues take real values if the dimensionless moments of inertia satisfy the condition
Otherwise, two proper numbers will be purely imaginary. If we build graphs of eigenvalues
Positive root of characteristic polynomial

Negative root of characteristic polynomial

findings
At least one eigenvalue with a positive real part speaks of the instability of the steady state of motion.
Now let's see, because condition (15) satisfies condition (3) that we adopted at the beginning. When the ratio between the moments of inertia, when
that is, being initially twisted around an axis with an intermediate between the maximum and minimum value of the moment of inertia, the nut behaves unstably, performs a revolution, and then again tries to find a stable position, and again performs a revolution. It is known that stable rotations of a free body are possible only around axes with maximum and minimum inertia moments.
If a
then we get the purely imaginary roots of the characteristic equation, and the first Lyapunov method does not unambiguously answer the question whether the motion will be stable in this case. But based on what the mechanics do not know today and on the oscillatory nature of solving linear equations with imaginary roots of the characteristic equation, one can assume periodic oscillations of the angular velocity vector around the steady state, which corresponds to the processes of precession and nutation.
In this regard, our planet, satisfying condition (16) will not experience the effect of Janibekov. So the global catastrophe with the change of poles does not threaten us.
This article was some warm-up. Perhaps we will come back to the “lamb nut”, but for now - thank my readers for their attention!
> To be continued ...
Source: https://habr.com/ru/post/264099/
All Articles