Accelerated course on notations in the theory of programming languages
Programmers are often faced with the problems of reading mathematical notations when they try to understand the theoretical foundations of a programming language. I also pushed with them in my theoretical research. Fortunately, the wonderful article by Jeremy Siek, whose translation I want to share with you, helped me a lot. I hope it will help many non-mathematician programmers.
With this post I want to help my friends with reading my other posts. This is an accelerated course on notations used in the theory of programming languages (TNG). For a much better study of the topic, I recommend “Types and Programming Languages” from Benjamin C. Pierce and “Semantic Engineering with PLT Redex” from Felleisen, Findler, and Flatt. I assume that the reader is an experienced programmer, but not so good at math and TNT. I will start with the basic definitions and try to quickly get you up to speed.
I suspect that many readers will be familiar with sets, tuples, and relationships, but if you are not familiar with inductive definitions, then read the “rules by definition” section below.
The main building block that we use in the TNG is a multitude, i.e. collection of objects (or items). For example, a set consisting of the first three natural numbers: {0, 1, 2}.
The only fact that matters is whether the object belongs to the set or not. It does not matter whether there are duplicates or what order the object appears in the set. For example, the set {0, 2, 1} is the same as the one above. Notation ∈ means "in". Thus, 1 ∈ {0, 1, 2} is true and 3 ∈ {0, 1, 2} is false. Sets can contain an infinite number of elements. For example, the set of all natural numbers (nonnegative integers), denoted by N.
')
Another building block is a tuple, i.e. ordered collection of objects. So (0, 1, 2) is a tuple of three elements and it differs from the tuple (0, 2, 1). The subscript t i stands for the i-th (with index i) element of the tuple t. For example, if t = (0, 2, 1), then t 1 = 0, t 2 = 2, t 3 = 1. Tuples always contain a finite number of elements and usually quite a bit. Sometimes to refer to tuples, angle brackets are used instead of round ones: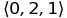 .
.
By combining tuples and sets we get relationships. Attitude is a multitude of tuples.
{(0, 1), (1,2), (2, 3), (3, 4), ...}
We often use relationships to display input values over the weekend. For example, we can think of the relation above as the mapping of a natural number to its follower, i.e. to the next greater natural number. The definition above is rather inaccurate due to the use of (...). Fortunately, there are more accurate notations for describing infinite sets and relations.
The main way in which we define infinite sets in the TNG is to provide a set of rules describing which elements are in the set. Let's use the name R for the set above. Then the following two rules will give us a precise definition of R. Note that the second rule is recursive in the sense that it refers to itself. This is a normal and fairly common situation.
When we use rules to define a set, we mean that the element is not in the set, if there is no way to use these rules to justify finding this element in the set. So (0, 0) does not belong to R, because it is impossible to substantiate with the help of the indicated rules that (0, 0) belongs to it.
Some rule sets are meaningless and do not define a set. For example, the rules should not contradict each other, like this:
The TNG textbook describes limitations for “good” rule sets, but we will not go into that. We will only say that at least one rule should be non-recursive and there should be no such logical contradictions.
A common notation for rules, as above, uses a horizontal line between “if” and “then”. For example, an equivalent definition for R is given as follows.
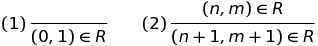
We omitted “for any natural numbers n and m” from rule 2. The convention is used, according to which variables, such as n and m, which appear in the rule, can be replaced by any object of the correct type. In this case, a natural number. Often, the “correct type” is something that can be guessed from the context of the conversation. In this case, natural numbers.
Suppose I say that some element is in R. Let's say (2, 3) ∈ R. You can answer that you do not believe me. To convince you, I need to show how the rules justify the fact that (2, 3) ∈ R. I have to show you the conclusion. The output is a chain of rules in which variables, such as n and m, are replaced with specific values and prerequisites, such as (n, m) ∈ R, are replaced with more specific conclusions.
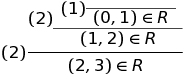
I marked each step in the derivation with a rule number. A whimsical name for what I call the “definition of rules” is an inductive definition.
It turns out that the use of rules to define sets, as we did above, is also suitable for determining the syntax of a programming language. Suppose we need to define a simple language for integer arithmetic. Let's call it Arith. It will contain expressions such as 1 + 3 and - (5 + 2). Recall that Z is a set of integers. Then the set of rules describing Arith will be:
The Backus-Naur form (BNF) is another common notation for writing rules that define the syntax of a language, which means the same thing. (There are several variants of the BNF. I forgot which one I use here.) The rule set is called grammar.
A vertical bar (meaning “or”) is often used to make the syntax more concise.
Arith :: = integer | "-" Arith | Arith "+" Arith | "(" Arith ")"
In TNT, we use a peculiar variant of the BNF, which replaces the name of the language being defined, in this case Arith, with a variable that is used to walk through the Arith elements. Now suppose we use the variable i as a placeholder for integers and e as a placeholder for Arith elements. Then we can write our grammar like this:
Notice that I omitted the brackets. As a rule, it is clear that brackets are allowed in any language. The concept of output coincides with the parse tree. They both demonstrate why a particular element is included in the set.
To describe a language is to describe what will happen when a program is launched in this language. That is what operational semantics does. In the case of Arith, we need to specify an integer result for each program. As mentioned above, we can use relationships to display input data on the result. And we usually do this in TNG. There are several different styles of relationships. The first, which we consider, is the semantics of a big step (big-step semantics), which displays the program directly on its result.
Define an Eval relation that maps Arith elements to integers. For example, the condition (- (2 + −5), 3) ∈ Eval should be satisfied. This relationship will be infinite (because there are an infinite number of programs on Arith). Again, we will use the rule set to define Eval. But before we begin, we introduce the abbreviation: means (e, i) ∈ Eval. Below we describe the rules defining Eval using horizontal bar notation. To make sure that we don’t miss a single program, we will create one rule for each Arith syntax rule (there are three of them). We will say that the rules are syntactically-oriented, when one rule corresponds to each syntactic rule of a language.
means (e, i) ∈ Eval. Below we describe the rules defining Eval using horizontal bar notation. To make sure that we don’t miss a single program, we will create one rule for each Arith syntax rule (there are three of them). We will say that the rules are syntactically-oriented, when one rule corresponds to each syntactic rule of a language.
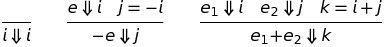
This may seem a little odd, that I defined "-" in terms of "-" and "+" in terms of "+". Is this a cyclical dependency? The answer is no. Plus and minus are the usual arithmetic operations for the integers each pass in the school. In this sense, it would be more strange for Arith not to use 32 or 64-bit arithmetic. A programmer implementing Arith could use the package to work with BigInteger to handle arithmetic.
The second and most common style of operational semantics is the semantics of a small step. In this style the relation does not display the program on its result. Instead, it maps the program to a slightly simplified program, in which some subexpression is replaced by its result. You can think of this style as a text replacement. To give an example of this style, we define the step relation. This relationship will contain the following elements, like many others:
Enter the abbreviation again: means (e1, e2) ∈ Step. And if we put the steps together, then
means (e1, e2) ∈ Step. And if we put the steps together, then 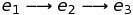 will mean
will mean  and
and  . The synonym for a step is the term “reduce” (reduce). The previous two-step example can now be written like this:
. The synonym for a step is the term “reduce” (reduce). The previous two-step example can now be written like this:
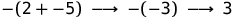
We now turn to the rules governing the relation Step. Here are five rules that we will explain below.
![\ begin {gather *} (1) \ frac {j = -i} {\ mathtt {-} i \ longrightarrow j} \ qquad (2) \ frac {k = i + j} {i \ mathtt {+} j \ longrightarrow k} \\ [3ex] (3) \ frac {e \ longrightarrow e '} {\ mathtt {-} e \ longrightarrow \ mathtt {-} e'} \ qquad (4) \ frac {e_1 \ longrightarrow e '_1} {e_1 \ mathtt {+} e_2 \ longrightarrow e'_1 \ mathtt {+} e_2} \ qquad (5) \ frac {e_2 \ longrightarrow e'_2} {i \ mathtt {+} e_2 \ longrightarrow i \ mathtt {+} e'_2} \ end {gather *}](https://habrastorage.org/getpro/habr/post_images/a72/c78/416/a72c784165e744663f825b7c38e0e676.png)
The rules (1) and (2) are the most interesting. They perform arithmetic. We call them the “computational reduction rules”. Rules (3-5) allow us to go into subexpressions to perform calculations. They are often referred to as congruence rules for reasons we will not go into now. Using the variable i in rule (5) means that the reduction occurs from left to right. In particular, we do not allow shortening the right expression from the + sign until the left expression is reduced to an integer.
Digression: The left-to-right order I considered here was chosen as a language designer. I could not define the order, allowing it to be vague. Our language has no side effects, so the order does not matter. However, most languages have side effects and they determine the order (but not all), so I thought that we should consider an example of how the order usually determines.
Time for an example. Let's look at the conclusion for the step: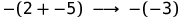
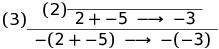
We have defined one calculation step, i.e. Step relationship. But we are not completely finished. We still have to define what it means to execute the program before completion. We do this by defining Eval 'in terms of the Step relationship. In other words, the relation Eval 'will contain any pairs (e, i) if the expression e is reduced to integer i in zero or more steps. There is a new notation here, which is explained further.
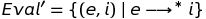
The notation {... ∣ ...} defines a set constructor. The expression to the left of the vertical bar defines the pattern for a typical set element and the expression to the right defines the restrictions on the set elements. Notation means zero or more steps. I would define these multi-step relationships using the rules:
means zero or more steps. I would define these multi-step relationships using the rules:
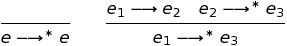
(I think of it in terms of Lisp-like lists. So, the first rule is nil, and the second cons.)
Many programming languages are statically typed, i.e. the compiler performs some validation checks before performing the actual compilation. Usually, during testing, the compiler makes sure that objects are used as they should. For example, that no one tries to use an integer as a function. The way in which the language developer specifies which particular checks should be performed is to define a type system for the language. Arith is so simple that there are no interesting type checks in it. Consider a more complex language that is used again and again in the TNG - lambda calculus (technically, lambda calculus with simplified typing). Lambda calculus consists only of anonymous functions. We will expand lambda calculus so that it includes our arithmetic expressions. Then our language will be defined by the following grammar.
The variable x lists parameter names, such as foo and g. The next two expressions (ee) to the right indicate the use of a function (or function call). If you are familiar with the C language, you can read e1 e2 as e1 (e2). In lambda calculus, functions take only one parameter, so a function call requires only one argument. The syntax λx: Te creates a function with one parameter x of type T (we will soon define the types) and a body consisting of the expression e. (Often people are mistaken in thinking that x is the name of a function. In fact, this is the name of the parameter, since functions are anonymous, that is, they do not have a name.) The return value of the function is the result of the expression e. Now we will think about what objects will exist during the execution of the program. These are integers and functions. We will create a set of types to describe the types of objects, using T to enumerate the set of types.

In functional type , T 1 is the parameter type, and T 2 is the return type.
, T 1 is the parameter type, and T 2 is the return type.
The work of the type system is to predict what type of value the expression result will have. For example, the expression - (5 + 2) must be of type Int, because the result - (5 + 2) is the number -3, which is an integer. As in the case of syntax definition or operational semantics of a language, TNT theorist uses relationships and rules to define a type system. We define the WellTyped relationship, which, as a first approximation, maps expressions to types. For example, it will hold (- (5 + 2), Int) ∈ WellTyped.
However, since The lambda calculus includes variables, we need some kind of analogue of the symbol table, a relationship, called a type environment, to keep track of which variables are of which type. The Greek letter Γ (gamma) is commonly used for this purpose. We must be able to create new types of environments from the old, with the ability to hide variables from external scopes. To determine the mathematical apparatus for these possibilities, we assume that Γ ∖ x is a relation the same as Γ, except that any tuple starting with x will be excluded. (Depending on the way the type system is defined, there can be a 0 or 1 tuple that starts with x, making the type environment a special kind of relation called a partial function.) We will write Γ, x: T for the operation Extending the type environment with the x variable, possibly overriding the previous definition, and defined as follows:
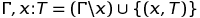
Let's pretend that
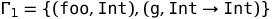
Then
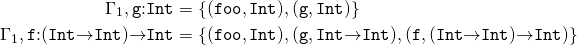
The type environment differs from the global symbol table in the compiler in that there can be more than one type environment, one for each scope. In addition, we do not update the type environment; instead, we create a new environment that is slightly different from the old one. From a programming point of view, the mathematical meta language that we use here is pure functional, i.e. It contains no side effects. The reader may worry that this leads to inefficiency, but remember that we are not writing a program here, we are writing a specification! The greatest value for us is understandable. And staying clean we can write more understandable things.
Returning to the WellTyped relation, instead of containing tuples of two elements (2-tuples, pairs), it will contain tuples of three elements (3-tuples, triples) of the form (Γ, e, T). Thus, we will attribute types to expressions in the context of a type environment. We introduce one more abbreviation (TNT theorists love abbreviations!). Will write instead of (Γ, e, T) ∈ WellTyped. Now we are ready to list the rules that define WellTyped.
instead of (Γ, e, T) ∈ WellTyped. Now we are ready to list the rules that define WellTyped.
![\ begin {gather *} \ frac {} {\ Gamma \ vdash i: \ mathtt {Int}} \ qquad \ frac {\ Gamma \ vdash e: \ mathtt {Int}} {\ Gamma \ vdash \ mathtt {-} e: \ mathtt {Int}} \ qquad \ frac {\ Gamma \ vdash e_1: \ mathtt {Int} \ quad \ Gamma \ vdash e_2: \ mathtt {Int}} {\ Gamma \ vdash e_1 \ mathtt {+} e_2 : \ mathtt {Int}} \\ [3ex] \ frac {(x, T) \ in \ Gamma} {\ Gamma \ vdash x: T} \ qquad \ frac {\ Gamma, x {:} T_1 \ vdash e : T_2} {\ Gamma \ vdash (\ lambda x {:} T_1. E): (T_1 \ to T_2)} \ qquad \ frac {\ Gamma \ vdash e_1: T \ to T '\ quad \ Gamma \ vdash e_2 : T} {\ Gamma \ vdash e_1 \, e_2: T '} \ end {gather *}](https://habrastorage.org/getpro/habr/post_images/491/925/cc3/491925cc3120afcc0dcce1e0829ca1d3.png)
Let's summarize for the rules above. Arithmetic operators work with integers. Variables get their types from the environment. Lambdas are functional types based on the type of their parameter and the output type of the result. The body of the lambda is checked using the lexical scoping environment, extended with the parameter of this lambda. And the use of the function does not violate the logic of the language as long as the type of the argument coincides with the type of the parameter.
This concludes this accelerated course on notations used in the theory of programming languages. This post only describes the basics, but a lot of additional notations that you will need are variations discussed here. Happy reading and feel free to ask questions in the comments.
Introduction
With this post I want to help my friends with reading my other posts. This is an accelerated course on notations used in the theory of programming languages (TNG). For a much better study of the topic, I recommend “Types and Programming Languages” from Benjamin C. Pierce and “Semantic Engineering with PLT Redex” from Felleisen, Findler, and Flatt. I assume that the reader is an experienced programmer, but not so good at math and TNT. I will start with the basic definitions and try to quickly get you up to speed.
Sets, tuples, relationships, and rule definitions
I suspect that many readers will be familiar with sets, tuples, and relationships, but if you are not familiar with inductive definitions, then read the “rules by definition” section below.
The sets
The main building block that we use in the TNG is a multitude, i.e. collection of objects (or items). For example, a set consisting of the first three natural numbers: {0, 1, 2}.
The only fact that matters is whether the object belongs to the set or not. It does not matter whether there are duplicates or what order the object appears in the set. For example, the set {0, 2, 1} is the same as the one above. Notation ∈ means "in". Thus, 1 ∈ {0, 1, 2} is true and 3 ∈ {0, 1, 2} is false. Sets can contain an infinite number of elements. For example, the set of all natural numbers (nonnegative integers), denoted by N.
')
Tuples
Another building block is a tuple, i.e. ordered collection of objects. So (0, 1, 2) is a tuple of three elements and it differs from the tuple (0, 2, 1). The subscript t i stands for the i-th (with index i) element of the tuple t. For example, if t = (0, 2, 1), then t 1 = 0, t 2 = 2, t 3 = 1. Tuples always contain a finite number of elements and usually quite a bit. Sometimes to refer to tuples, angle brackets are used instead of round ones:
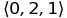 .
.Relations
By combining tuples and sets we get relationships. Attitude is a multitude of tuples.
{(0, 1), (1,2), (2, 3), (3, 4), ...}
We often use relationships to display input values over the weekend. For example, we can think of the relation above as the mapping of a natural number to its follower, i.e. to the next greater natural number. The definition above is rather inaccurate due to the use of (...). Fortunately, there are more accurate notations for describing infinite sets and relations.
Definition rules
The main way in which we define infinite sets in the TNG is to provide a set of rules describing which elements are in the set. Let's use the name R for the set above. Then the following two rules will give us a precise definition of R. Note that the second rule is recursive in the sense that it refers to itself. This is a normal and fairly common situation.
- (0, 1) ∈ R.
- For any positive integers n and m, if (n, m) ∈ R, then (n + 1, m + 1) ∈ R.
When we use rules to define a set, we mean that the element is not in the set, if there is no way to use these rules to justify finding this element in the set. So (0, 0) does not belong to R, because it is impossible to substantiate with the help of the indicated rules that (0, 0) belongs to it.
Some rule sets are meaningless and do not define a set. For example, the rules should not contradict each other, like this:
- (0, 1) ∈ R.
- (0, 1) ∉ R.
The TNG textbook describes limitations for “good” rule sets, but we will not go into that. We will only say that at least one rule should be non-recursive and there should be no such logical contradictions.
A common notation for rules, as above, uses a horizontal line between “if” and “then”. For example, an equivalent definition for R is given as follows.
We omitted “for any natural numbers n and m” from rule 2. The convention is used, according to which variables, such as n and m, which appear in the rule, can be replaced by any object of the correct type. In this case, a natural number. Often, the “correct type” is something that can be guessed from the context of the conversation. In this case, natural numbers.
Suppose I say that some element is in R. Let's say (2, 3) ∈ R. You can answer that you do not believe me. To convince you, I need to show how the rules justify the fact that (2, 3) ∈ R. I have to show you the conclusion. The output is a chain of rules in which variables, such as n and m, are replaced with specific values and prerequisites, such as (n, m) ∈ R, are replaced with more specific conclusions.
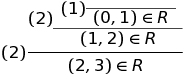
I marked each step in the derivation with a rule number. A whimsical name for what I call the “definition of rules” is an inductive definition.
Language and Grammar Syntax
It turns out that the use of rules to define sets, as we did above, is also suitable for determining the syntax of a programming language. Suppose we need to define a simple language for integer arithmetic. Let's call it Arith. It will contain expressions such as 1 + 3 and - (5 + 2). Recall that Z is a set of integers. Then the set of rules describing Arith will be:
- For any i ∈ Z, it is true that i ∈ Arith.
- For any e, if e ∈ Arith, then -e ∈ Arith.
- For any e1 and e2, if e1 ∈ Arith and e2 ∈ Arith, then e1 + e2 ∈ Arith.
- For any e, if e ∈ Arith, then (e) ∈ Arith.
The Backus-Naur form (BNF) is another common notation for writing rules that define the syntax of a language, which means the same thing. (There are several variants of the BNF. I forgot which one I use here.) The rule set is called grammar.
Arith :: = integer
Arith :: = "-" Arith
Arith :: = Arith "+" Arith
Arith :: = "(" Arith ")"
A vertical bar (meaning “or”) is often used to make the syntax more concise.
Arith :: = integer | "-" Arith | Arith "+" Arith | "(" Arith ")"
In TNT, we use a peculiar variant of the BNF, which replaces the name of the language being defined, in this case Arith, with a variable that is used to walk through the Arith elements. Now suppose we use the variable i as a placeholder for integers and e as a placeholder for Arith elements. Then we can write our grammar like this:
e :: = i ∣ −e ∣ e + e
Notice that I omitted the brackets. As a rule, it is clear that brackets are allowed in any language. The concept of output coincides with the parse tree. They both demonstrate why a particular element is included in the set.
Operational semantics
To describe a language is to describe what will happen when a program is launched in this language. That is what operational semantics does. In the case of Arith, we need to specify an integer result for each program. As mentioned above, we can use relationships to display input data on the result. And we usually do this in TNG. There are several different styles of relationships. The first, which we consider, is the semantics of a big step (big-step semantics), which displays the program directly on its result.
Big-step semantics
Define an Eval relation that maps Arith elements to integers. For example, the condition (- (2 + −5), 3) ∈ Eval should be satisfied. This relationship will be infinite (because there are an infinite number of programs on Arith). Again, we will use the rule set to define Eval. But before we begin, we introduce the abbreviation:
 means (e, i) ∈ Eval. Below we describe the rules defining Eval using horizontal bar notation. To make sure that we don’t miss a single program, we will create one rule for each Arith syntax rule (there are three of them). We will say that the rules are syntactically-oriented, when one rule corresponds to each syntactic rule of a language.
means (e, i) ∈ Eval. Below we describe the rules defining Eval using horizontal bar notation. To make sure that we don’t miss a single program, we will create one rule for each Arith syntax rule (there are three of them). We will say that the rules are syntactically-oriented, when one rule corresponds to each syntactic rule of a language.This may seem a little odd, that I defined "-" in terms of "-" and "+" in terms of "+". Is this a cyclical dependency? The answer is no. Plus and minus are the usual arithmetic operations for the integers each pass in the school. In this sense, it would be more strange for Arith not to use 32 or 64-bit arithmetic. A programmer implementing Arith could use the package to work with BigInteger to handle arithmetic.
Small-step semantics semantics
The second and most common style of operational semantics is the semantics of a small step. In this style the relation does not display the program on its result. Instead, it maps the program to a slightly simplified program, in which some subexpression is replaced by its result. You can think of this style as a text replacement. To give an example of this style, we define the step relation. This relationship will contain the following elements, like many others:
(- (2 + -5), - (- 3)) ∈ Step
(- (- 3), 3) ∈ Step
Enter the abbreviation again:
 means (e1, e2) ∈ Step. And if we put the steps together, then
means (e1, e2) ∈ Step. And if we put the steps together, then 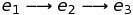 will mean
will mean  and
and  . The synonym for a step is the term “reduce” (reduce). The previous two-step example can now be written like this:
. The synonym for a step is the term “reduce” (reduce). The previous two-step example can now be written like this: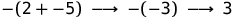
We now turn to the rules governing the relation Step. Here are five rules that we will explain below.
![\ begin {gather *} (1) \ frac {j = -i} {\ mathtt {-} i \ longrightarrow j} \ qquad (2) \ frac {k = i + j} {i \ mathtt {+} j \ longrightarrow k} \\ [3ex] (3) \ frac {e \ longrightarrow e '} {\ mathtt {-} e \ longrightarrow \ mathtt {-} e'} \ qquad (4) \ frac {e_1 \ longrightarrow e '_1} {e_1 \ mathtt {+} e_2 \ longrightarrow e'_1 \ mathtt {+} e_2} \ qquad (5) \ frac {e_2 \ longrightarrow e'_2} {i \ mathtt {+} e_2 \ longrightarrow i \ mathtt {+} e'_2} \ end {gather *}](https://habrastorage.org/getpro/habr/post_images/a72/c78/416/a72c784165e744663f825b7c38e0e676.png)
The rules (1) and (2) are the most interesting. They perform arithmetic. We call them the “computational reduction rules”. Rules (3-5) allow us to go into subexpressions to perform calculations. They are often referred to as congruence rules for reasons we will not go into now. Using the variable i in rule (5) means that the reduction occurs from left to right. In particular, we do not allow shortening the right expression from the + sign until the left expression is reduced to an integer.
Digression: The left-to-right order I considered here was chosen as a language designer. I could not define the order, allowing it to be vague. Our language has no side effects, so the order does not matter. However, most languages have side effects and they determine the order (but not all), so I thought that we should consider an example of how the order usually determines.
Time for an example. Let's look at the conclusion for the step:
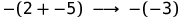
We have defined one calculation step, i.e. Step relationship. But we are not completely finished. We still have to define what it means to execute the program before completion. We do this by defining Eval 'in terms of the Step relationship. In other words, the relation Eval 'will contain any pairs (e, i) if the expression e is reduced to integer i in zero or more steps. There is a new notation here, which is explained further.
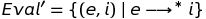
The notation {... ∣ ...} defines a set constructor. The expression to the left of the vertical bar defines the pattern for a typical set element and the expression to the right defines the restrictions on the set elements. Notation
 means zero or more steps. I would define these multi-step relationships using the rules:
means zero or more steps. I would define these multi-step relationships using the rules:(I think of it in terms of Lisp-like lists. So, the first rule is nil, and the second cons.)
Type systems (with lambda calculus as an example)
Many programming languages are statically typed, i.e. the compiler performs some validation checks before performing the actual compilation. Usually, during testing, the compiler makes sure that objects are used as they should. For example, that no one tries to use an integer as a function. The way in which the language developer specifies which particular checks should be performed is to define a type system for the language. Arith is so simple that there are no interesting type checks in it. Consider a more complex language that is used again and again in the TNG - lambda calculus (technically, lambda calculus with simplified typing). Lambda calculus consists only of anonymous functions. We will expand lambda calculus so that it includes our arithmetic expressions. Then our language will be defined by the following grammar.
e :: = i ∣ −e ∣ e + e ∣ x ∣ ee ∣ λx: Te
The variable x lists parameter names, such as foo and g. The next two expressions (ee) to the right indicate the use of a function (or function call). If you are familiar with the C language, you can read e1 e2 as e1 (e2). In lambda calculus, functions take only one parameter, so a function call requires only one argument. The syntax λx: Te creates a function with one parameter x of type T (we will soon define the types) and a body consisting of the expression e. (Often people are mistaken in thinking that x is the name of a function. In fact, this is the name of the parameter, since functions are anonymous, that is, they do not have a name.) The return value of the function is the result of the expression e. Now we will think about what objects will exist during the execution of the program. These are integers and functions. We will create a set of types to describe the types of objects, using T to enumerate the set of types.

In functional type
 , T 1 is the parameter type, and T 2 is the return type.
, T 1 is the parameter type, and T 2 is the return type.The work of the type system is to predict what type of value the expression result will have. For example, the expression - (5 + 2) must be of type Int, because the result - (5 + 2) is the number -3, which is an integer. As in the case of syntax definition or operational semantics of a language, TNT theorist uses relationships and rules to define a type system. We define the WellTyped relationship, which, as a first approximation, maps expressions to types. For example, it will hold (- (5 + 2), Int) ∈ WellTyped.
However, since The lambda calculus includes variables, we need some kind of analogue of the symbol table, a relationship, called a type environment, to keep track of which variables are of which type. The Greek letter Γ (gamma) is commonly used for this purpose. We must be able to create new types of environments from the old, with the ability to hide variables from external scopes. To determine the mathematical apparatus for these possibilities, we assume that Γ ∖ x is a relation the same as Γ, except that any tuple starting with x will be excluded. (Depending on the way the type system is defined, there can be a 0 or 1 tuple that starts with x, making the type environment a special kind of relation called a partial function.) We will write Γ, x: T for the operation Extending the type environment with the x variable, possibly overriding the previous definition, and defined as follows:
Let's pretend that
Then
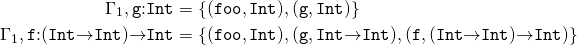
The type environment differs from the global symbol table in the compiler in that there can be more than one type environment, one for each scope. In addition, we do not update the type environment; instead, we create a new environment that is slightly different from the old one. From a programming point of view, the mathematical meta language that we use here is pure functional, i.e. It contains no side effects. The reader may worry that this leads to inefficiency, but remember that we are not writing a program here, we are writing a specification! The greatest value for us is understandable. And staying clean we can write more understandable things.
Returning to the WellTyped relation, instead of containing tuples of two elements (2-tuples, pairs), it will contain tuples of three elements (3-tuples, triples) of the form (Γ, e, T). Thus, we will attribute types to expressions in the context of a type environment. We introduce one more abbreviation (TNT theorists love abbreviations!). Will write
 instead of (Γ, e, T) ∈ WellTyped. Now we are ready to list the rules that define WellTyped.
instead of (Γ, e, T) ∈ WellTyped. Now we are ready to list the rules that define WellTyped.![\ begin {gather *} \ frac {} {\ Gamma \ vdash i: \ mathtt {Int}} \ qquad \ frac {\ Gamma \ vdash e: \ mathtt {Int}} {\ Gamma \ vdash \ mathtt {-} e: \ mathtt {Int}} \ qquad \ frac {\ Gamma \ vdash e_1: \ mathtt {Int} \ quad \ Gamma \ vdash e_2: \ mathtt {Int}} {\ Gamma \ vdash e_1 \ mathtt {+} e_2 : \ mathtt {Int}} \\ [3ex] \ frac {(x, T) \ in \ Gamma} {\ Gamma \ vdash x: T} \ qquad \ frac {\ Gamma, x {:} T_1 \ vdash e : T_2} {\ Gamma \ vdash (\ lambda x {:} T_1. E): (T_1 \ to T_2)} \ qquad \ frac {\ Gamma \ vdash e_1: T \ to T '\ quad \ Gamma \ vdash e_2 : T} {\ Gamma \ vdash e_1 \, e_2: T '} \ end {gather *}](https://habrastorage.org/getpro/habr/post_images/491/925/cc3/491925cc3120afcc0dcce1e0829ca1d3.png)
Let's summarize for the rules above. Arithmetic operators work with integers. Variables get their types from the environment. Lambdas are functional types based on the type of their parameter and the output type of the result. The body of the lambda is checked using the lexical scoping environment, extended with the parameter of this lambda. And the use of the function does not violate the logic of the language as long as the type of the argument coincides with the type of the parameter.
Conclusion
This concludes this accelerated course on notations used in the theory of programming languages. This post only describes the basics, but a lot of additional notations that you will need are variations discussed here. Happy reading and feel free to ask questions in the comments.
Source: https://habr.com/ru/post/263951/
All Articles