Sampling schemes
The sampling scheme is a detailed description of what data will be obtained and in what way. There are many schemes for selection in the sample , so you need to choose one that will give the most representative results for research. The representativeness of the sample is the compliance of the characteristics of the sample with the characteristics of the population.
Ideally, it is better to work with the entire population, but it takes a lot of time and resources. Therefore, it is possible to investigate only a part of it, which is called sampling. Then the elements that are in the sample are examined. Based on the values obtained, unknown elements of the sample are estimated.

')
The idea is to transfer the results to the entire population. Therefore, the sample should be representative. In other words, it is proportional to both subgroups and the entire population, and does not exclude any particular groups.
The sample should be as large as possible in order to avoid erroneous judgments. In fact, the sample can be any subset of the population.
If the sample is not representative enough - the study will be considered biased. If it is not big enough - inaccurate.
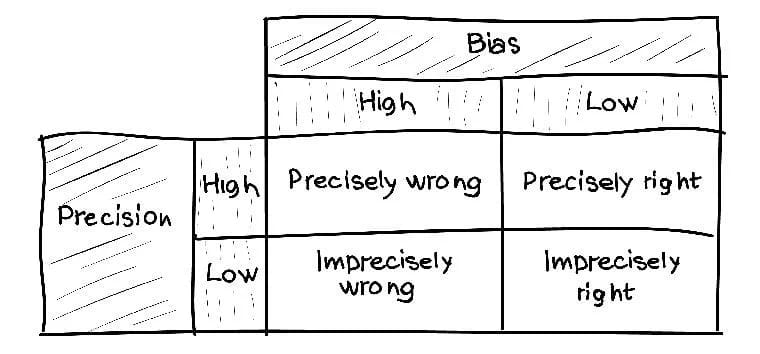
If you choose the right link between the sample and the population, then you can make the right conclusions about the nature of the whole population. It is better to be possibly right than not exactly right.
Probabilistic samples imply that the researcher is absolutely sure of the links of the sample with the general population. If the links are not traceable or not all elements of the population are available, an improbable sample is used.
The selection scheme is to conduct a series of tests without returning the item to the general population. Each element of the aggregate has the same chance of being sampled.
From the general population N one element is randomly selected, the probability of an element entering the sample is 1 / N. Then a second element is selected from the N-1 sample with a probability of 1 / (N-1), and so on up to the n-th element with a probability of 1 / (Nn).
The selection comes from an ordered list of N items. Let a certain number ε (1 <ε <0) and a set of N independent realizations of a random variable ε1… εN uniformly distributed on [0,1] be preassigned. Each element k is assigned a value. If εk <π, then this element is selected, otherwise not. The possibility that the element will be chosen is equal to π for each of the N elements. Thus, each element that is sampled is a binomially distributed quantity.
Let N be the size of the general population. a is a fixed number. a ∈ N. The first element of the sample is chosen randomly among the first a elements of the population. The selected number r 1≤ r ≤ a is called a random start (start), and the number a is a sampling interval. Each element [1,2 ... a] has the same probability of being selected, equal to 1 / a. Next, the elements fall into the sample in increments of a.
You can get different samples, each of which has the same probability of being selected.
In all the above schemes, the element has not been able to get into the sample more than 1 time.
This is logical, since when you re-enable the item, new information is not added. But in this case, some estimates have very simple statistical properties, which makes it possible to investigate rather complex selection procedures.
For example, there are m independent selections of elements from the general population of size N with the same probabilities 1 / N. The selected item is returned to the population. Thus, all N elements participate in the selection all the time.
Assumes that all numbers of the population should be well mixed. Then the researcher takes every second item from the list.
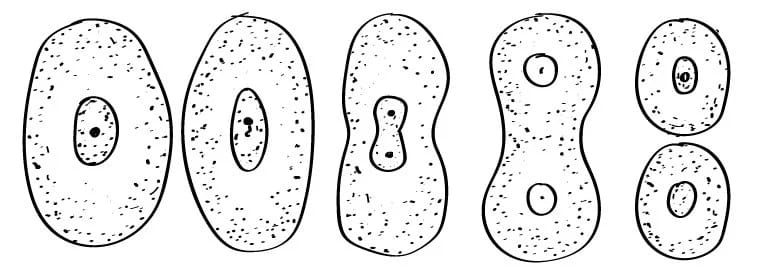
In this selection, the general population is divided into groups that do not overlap. These groups are called strata. The elements in each stratum are homogeneous for certain characteristics. Elements are selected in each stratum. The selection method can be any, and not necessarily the same in each stratum. Selection from one stratum does not depend on other strata.
The selection strategy in this case becomes more effective. The more the characteristic under study changes, the larger the sample will be for a more accurate estimate. And if we break the aggregate into strata, in which the characteristics differ little, then a small sample of each stratum will be enough to evaluate the whole aggregate.
Example: study of the level of income in the world. First, the whole world is divided into strata, namely countries. These are areas that do not overlap, then the study is conducted for each country separately.
In this case, it is difficult to estimate the probability of hitting each element of the aggregate in the sample. Researchers using these methods cannot draw accurate conclusions about the general population.
If direct selection from a population is not possible, the elements of the general population are combined into clusters.
Cluster selection can take place in one stage, then clusters are selected first, and then all elements of selected clusters are examined. For example, when exploring a city, a cluster could be a family or residents of the same house.
If the selection is carried out in two stages, then the aggregate is divided into clusters, which consist of other, smaller clusters. At the first stage, a probabilistic sample of primary clusters is obtained. In the second stage, elements are selected from the primary clusters.
The procedure may consist of three or more stages, then this scheme is called a multi-stage.
Items are selected based on whether they are easily accessible. Such samples are very easy to make, but there is not a single guarantee that it will be representative.
Usually used in selecting candidates from a specific small group of experts. One person is selected for questioning, then he must advise several other people, and so on.
Ideally, it is better to work with the entire population, but it takes a lot of time and resources. Therefore, it is possible to investigate only a part of it, which is called sampling. Then the elements that are in the sample are examined. Based on the values obtained, unknown elements of the sample are estimated.

')
The basic principles of selection in the sample
The idea is to transfer the results to the entire population. Therefore, the sample should be representative. In other words, it is proportional to both subgroups and the entire population, and does not exclude any particular groups.
The sample should be as large as possible in order to avoid erroneous judgments. In fact, the sample can be any subset of the population.
If the sample is not representative enough - the study will be considered biased. If it is not big enough - inaccurate.

If you choose the right link between the sample and the population, then you can make the right conclusions about the nature of the whole population. It is better to be possibly right than not exactly right.
Selection schemes for probability samples
Probabilistic samples imply that the researcher is absolutely sure of the links of the sample with the general population. If the links are not traceable or not all elements of the population are available, an improbable sample is used.
Based on the draw
The selection scheme is to conduct a series of tests without returning the item to the general population. Each element of the aggregate has the same chance of being sampled.
From the general population N one element is randomly selected, the probability of an element entering the sample is 1 / N. Then a second element is selected from the N-1 sample with a probability of 1 / (N-1), and so on up to the n-th element with a probability of 1 / (Nn).
Bernoulli selection
The selection comes from an ordered list of N items. Let a certain number ε (1 <ε <0) and a set of N independent realizations of a random variable ε1… εN uniformly distributed on [0,1] be preassigned. Each element k is assigned a value. If εk <π, then this element is selected, otherwise not. The possibility that the element will be chosen is equal to π for each of the N elements. Thus, each element that is sampled is a binomially distributed quantity.
Systematic selection
Let N be the size of the general population. a is a fixed number. a ∈ N. The first element of the sample is chosen randomly among the first a elements of the population. The selected number r 1≤ r ≤ a is called a random start (start), and the number a is a sampling interval. Each element [1,2 ... a] has the same probability of being selected, equal to 1 / a. Next, the elements fall into the sample in increments of a.
You can get different samples, each of which has the same probability of being selected.
Simple random selection with return
In all the above schemes, the element has not been able to get into the sample more than 1 time.
This is logical, since when you re-enable the item, new information is not added. But in this case, some estimates have very simple statistical properties, which makes it possible to investigate rather complex selection procedures.
For example, there are m independent selections of elements from the general population of size N with the same probabilities 1 / N. The selected item is returned to the population. Thus, all N elements participate in the selection all the time.
Proportional selection: with and without return
Assumes that all numbers of the population should be well mixed. Then the researcher takes every second item from the list.

Stratified selection
In this selection, the general population is divided into groups that do not overlap. These groups are called strata. The elements in each stratum are homogeneous for certain characteristics. Elements are selected in each stratum. The selection method can be any, and not necessarily the same in each stratum. Selection from one stratum does not depend on other strata.

The selection strategy in this case becomes more effective. The more the characteristic under study changes, the larger the sample will be for a more accurate estimate. And if we break the aggregate into strata, in which the characteristics differ little, then a small sample of each stratum will be enough to evaluate the whole aggregate.
Example: study of the level of income in the world. First, the whole world is divided into strata, namely countries. These are areas that do not overlap, then the study is conducted for each country separately.
Selection schemes for improbable samples
In this case, it is difficult to estimate the probability of hitting each element of the aggregate in the sample. Researchers using these methods cannot draw accurate conclusions about the general population.
Cluster selection
If direct selection from a population is not possible, the elements of the general population are combined into clusters.
Cluster selection can take place in one stage, then clusters are selected first, and then all elements of selected clusters are examined. For example, when exploring a city, a cluster could be a family or residents of the same house.
If the selection is carried out in two stages, then the aggregate is divided into clusters, which consist of other, smaller clusters. At the first stage, a probabilistic sample of primary clusters is obtained. In the second stage, elements are selected from the primary clusters.
The procedure may consist of three or more stages, then this scheme is called a multi-stage.
Typical selection
Items are selected based on whether they are easily accessible. Such samples are very easy to make, but there is not a single guarantee that it will be representative.
Snowball
Usually used in selecting candidates from a specific small group of experts. One person is selected for questioning, then he must advise several other people, and so on.
Abstract
- Samples are probabilistic and improbable.
- If the wrong selection method in the sample. research may be biased or inaccurate.
- It is better to be possibly right than not exactly right.
Source: https://habr.com/ru/post/263931/
All Articles