The finite element method on the example of the Poisson equation
In this article I would like to present the implementation of the finite element method on the example of the Poisson equation . Consider the task:

with homogeneous boundary condition
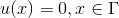
Where
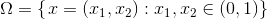


')
I need to find a function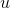 solving a given equation.
solving a given equation.
Decision
Multiply the initial equation by the function , continuous , piecewise continuously differentiable and equal to zero at the edges, and integrate the resulting equation over the entire domain
, continuous , piecewise continuously differentiable and equal to zero at the edges, and integrate the resulting equation over the entire domain 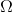 .
.
After applying the integration formula in parts , we obtain the following equation
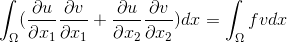
We introduce on the area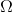 square grid with a pitch
square grid with a pitch 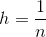 :
:

and each square is divided by a diagonal parallel to the bisector of the first coordinate angle:
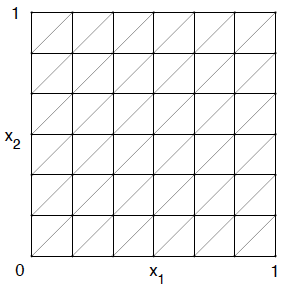
We get a split area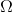 on triangular elements
on triangular elements 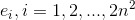 - area triangulation
- area triangulation 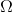 . This type of triangulation is called the Friedrichs-Keller triangulation.
. This type of triangulation is called the Friedrichs-Keller triangulation.
We will look for an approximate solution of this equation as a function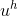 equal to zero on the boundary (boundary condition), continuous on the region
equal to zero on the boundary (boundary condition), continuous on the region 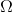 and linear on each received element of triangulation.
and linear on each received element of triangulation.
Function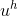 can be represented as follows:
can be represented as follows:
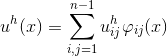
where the function values at the point defined as follows:
defined as follows:
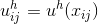

Substituting the function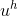 in the first equation, having carried out the transformations and the removal of constants from under the integral sign, we reduce the problem for each basis function to the calculation of integrals of the form:
in the first equation, having carried out the transformations and the removal of constants from under the integral sign, we reduce the problem for each basis function to the calculation of integrals of the form:

The value of the integral can be non-zero only if the basis functions under the integral sign have a non-empty common domain. By construction, each element has three vertices. A vertex can be common for up to 6 triangles:
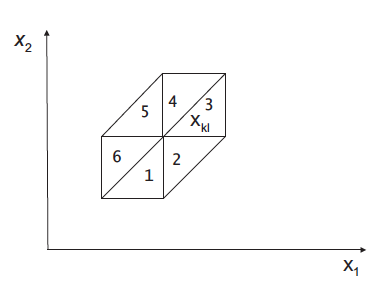
with the corresponding values of derivatives for each of 6 cases:

After calculating the integral equation with number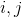 would look like this:
would look like this:
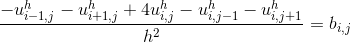
Where

and when small enough :
:
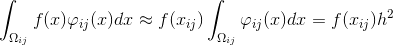
Therefore, the equation can be rewritten as follows:
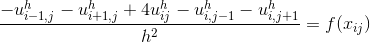
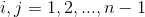
Adding boundary conditions, namely:
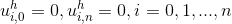

we get the complete SLAR, solving which, we find the values of the function at the grid points.
Many thanks RZ Dautov and M.M. Karchevsky for excellent literature!

with homogeneous boundary condition
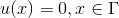
Where
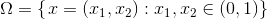


')
I need to find a function
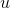 solving a given equation.
solving a given equation.Decision
Multiply the initial equation by the function
 , continuous , piecewise continuously differentiable and equal to zero at the edges, and integrate the resulting equation over the entire domain
, continuous , piecewise continuously differentiable and equal to zero at the edges, and integrate the resulting equation over the entire domain 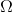 .
.After applying the integration formula in parts , we obtain the following equation
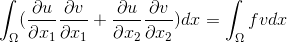
We introduce on the area
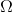 square grid with a pitch
square grid with a pitch 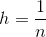 :
:
and each square is divided by a diagonal parallel to the bisector of the first coordinate angle:

We get a split area
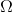 on triangular elements
on triangular elements 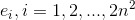 - area triangulation
- area triangulation  . This type of triangulation is called the Friedrichs-Keller triangulation.
. This type of triangulation is called the Friedrichs-Keller triangulation.We will look for an approximate solution of this equation as a function
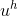 equal to zero on the boundary (boundary condition), continuous on the region
equal to zero on the boundary (boundary condition), continuous on the region  and linear on each received element of triangulation.
and linear on each received element of triangulation.Function
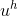 can be represented as follows:
can be represented as follows: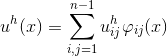
where the function values at the point
 defined as follows:
defined as follows: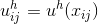

Substituting the function
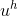 in the first equation, having carried out the transformations and the removal of constants from under the integral sign, we reduce the problem for each basis function to the calculation of integrals of the form:
in the first equation, having carried out the transformations and the removal of constants from under the integral sign, we reduce the problem for each basis function to the calculation of integrals of the form:
The value of the integral can be non-zero only if the basis functions under the integral sign have a non-empty common domain. By construction, each element has three vertices. A vertex can be common for up to 6 triangles:

with the corresponding values of derivatives for each of 6 cases:

After calculating the integral equation with number
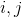 would look like this:
would look like this: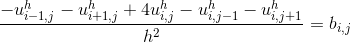
Where

and when small enough
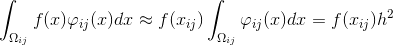
Therefore, the equation can be rewritten as follows:
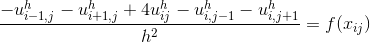
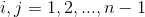
Adding boundary conditions, namely:
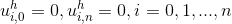

we get the complete SLAR, solving which, we find the values of the function at the grid points.
Many thanks RZ Dautov and M.M. Karchevsky for excellent literature!
Source: https://habr.com/ru/post/263597/
All Articles