Content

1. What is a tensor and what is it for?
2. Vector and tensor operations. Ranks of tensors
3. Curved coordinates
4. Dynamics of a point in the tensor representation
5. Actions on tensors and some other theoretical questions
6. Kinematics of free solid. Nature of angular velocity
7. The final turn of a solid. Rotation tensor properties and method for calculating it
8. On convolutions of the Levi-Civita tensor
9. Conclusion of the angular velocity tensor through the parameters of the final rotation. Apply head and maxima
10. Get the angular velocity vector. We work on the shortcomings
11. Acceleration of the point of the body with free movement. Solid Corner Acceleration
12. Rodrig – Hamilton parameters in solid kinematics
13. SKA Maxima in problems of transformation of tensor expressions. Angular velocity and acceleration in the parameters of Rodrig-Hamilton
14. Non-standard introduction to solid body dynamics
15. Non-free rigid motion
16. Properties of the inertia tensor of a solid
17. Sketch of nut Janibekov
18. Mathematical modeling of the Janibekov effect

Introduction

In this article we will solve two questions - we will get expressions for the angular velocity and angular acceleration using the Rodrig – Hamilton parameters, which we talked about in more detail than planned in the previous article . And at the same time we will demonstrate how you can use the open SKA Maxima for this purpose, which, as it turned out, copes well with tensors, and with certain skills, it can be a great help in solving scientific problems. For me, Maxima is a new product, before that I worked with Maple and quite a bit with Mathematica. Therefore, perhaps some of the techniques I use may seem unprofessional.
')

SKA is ready to help us and is waiting for a reasonable team ...


Last time, we stopped at what showed how quaternion algebra can be used to represent a transformation of a turn. Knowing the direction of the axis of rotation, given by the ort and the angle to rotate the coordinate system you can build a unit quaternion to the components

and then, the direct transformation of the rotation of the vector reduced to multiplication of quaternions

and the inverse transform

We have shown that the transformations (2) and (3) carried out directly on the vector give the Rodrigue formula describing the final turn. Now our goal is to connect the parameters of the rotation quaternion with the rotation tensor and pseudovectors of angular velocity and angular acceleration.

1. The rotation tensor in the parameters of Rodrigues-Hamilton

We already know the expression for the rotation tensor



We introduce a quaternion by presenting its vector part by contravariant components.



In this case, substitution (5) into (4) can be performed manually, this process does not imply anything extraordinary. But we will do everything in Maxima, at the same time preparing some basic data for further work. We configure Maxima for work with tensors in three-dimensional space

/*   */ kill(all); /*         LaTeX  */ load(itensor); load(tentex); /*         */ imetric(g); idim(3); 

Enter the expression (4) of the rotation tensor

 B:ishow(2*sin(phi/2)^2*u([],[m])*u([k],[]) + (cos(phi/2)^2 - sin(phi/2)^2)*kdelta([k],[m]) + 2*sin(phi/2)*cos(phi/2)*g([],[m,i])*'levi_civita([i,j,k],[])*u([],[j]))$ 

Pay attention to the nuance - we moved to half corners. Otherwise, when trying to simplify trigonometry, Maxima will not simplify anything, even setting the halfangles flag, which includes taking into account half-argument formulas, does not help. This is the first crutch that I had to use. Perhaps unknowingly.

Set the relationship between the parameters of the final rotation and the components of the quaternion

 Lambda0:p0 = cos(phi/2); Lambda:ishow(p([],[j]) = sin(phi/2)*u([],[j]))$ 

Here, for brevity (laziness to enter lambda each time), the components of the quaternion are indicated by the letter p

Express the orth of the rotation axis through the vector part of the quaternion

 Solv1:ishow(solve(Lambda, u([],[j])))$ 

outputting the solution to the equation as an array of expressions



In the resulting expression, it is necessary to omit the index, since the rotation tensor contains the covariant components of the rotation form. To do this, we collapse the previously obtained expression with the metric tensor

 u_k:ishow(contract(Solv1[1]*g([k,j],[])))$ 

In addition, we replace the index j with m in the covariant components

 um:ishow(subst(m, j, Solv1[1]))$ 

As a result, we get two expressions ready for substitution in the rotation tensor



Now we can substitute the components of the ort of the axis of rotation into the expression for the rotation tensor. The subst() setting function in this case takes two arguments — an expression that needs to be substituted into the expression that comes with the second argument. In this case, in the transformed expression, the left side of the first argument is searched for and replaced with its right side.

 B_1:ishow(subst(u_k, B))$ B_1:ishow(subst(um, B_1))$ B_1:ishow(subst(Solv1[1], B_1))$ 

At the exit we have



Great, now the components of the vector part of the quaternion appear in the rotation tensor. Now simplify trigonometry

 B_2:ishow(trigsimp(B_1))$ 

The trigsim() function simplifies trigonometric expressions. In this case, as written in the documentation, takes into account the basic basic trigonometric identity and the parity / oddness of trigonometric functions. However, whether the loading of a package of tensor algebra has such an effect, this function stumbles upon the simplification of fractions containing functions of single and half arguments, even when the flag is raised, which was mentioned above. Nevertheless, we carried out the preparatory work and at the output we obtain a simplified formula



It remains to replace the squares of the cosine and sine of the half angle of rotation by the scalar parameter of the quaternion, for which we perform the substitution and simplification in the form of opening the brackets

 B_3:ishow(subst(p0,rhs(Lambda0), B_2))$ B_3:ishow(expand(subst(1-p0^2,sin(phi/2)^2, B_3)))$ 

And, to admire the result, we derive it in LaTeX

 tentex(B_3); 

I added only the left part to the displayed code.



It can be seen that Maxima generates LaTeX-notation, which is very close to the natural mathematical notation, which cannot be said about Maple, which prepares a monstrous code containing all the conventions adopted by it in the derivation of readable formulas. The terms containing the Kronecker delta will be grouped and we will take the common factor out of the brackets independently. Well, back to the place of "lambda"



We have obtained the expression of the rotation tensor in terms of the Rodrigues-Hamilton parameters. From this tensor, one can go to any other parameters describing the orientation of a solid body in space.

Warm-up can be considered over. More serious work lies ahead.

2. Pseudovector of angular velocity in the parameters of Rodrigues-Hamilton

We introduce in Maxima an expression for the pseudovector of angular velocity already known to us. In natural form, it looks like this.



And in Maxima it will go with the replacement of functions of single angles by equivalent functions of half

 Omega:ishow(2*sin(phi/2)^2*'levi_civita([],[i,m,r])*u([i],[])*diff(u([m],[]),t) + diff(u([],[r]),t)*2*sin(phi/2)*cos(phi/2) + u([],[r])*diff(phi, t))$ 

Let me remind you that the Levi-Civita tensor, especially if you plan to simplify the expression using its properties, is better to introduce with suppression of the calculation. Otherwise, Maxima will turn it into a generalized Kronecker delta, and this is not part of our plans. To suppress the calculation, put an apostrophe before the name of the function that defines this tensor.

We lower the indices and rename the indices of the orth of rotation, in accordance with the designation of the indices in the angular velocity tensor

 u_i:ishow(contract(Solv1[1]*g([i,j],[])))$ u_m:ishow(subst(m, i, u_i))$ ur:ishow(subst(r, j, Solv1[1]))$ 

We receive expressions which we will use in substitutions



We will need derivatives of the ort of the axis of rotation and the angle of rotation. It is necessary to get them expressed through quaternion parameters.

 /*        */ du_mdt:ishow(diff(u_m, t))$ /*       */ dLambda0dt:diff(Lambda0, t); /*     */ Solv2:solve(dLambda0dt, diff(phi,t)); 

Maxima will perform all operations quite correctly.



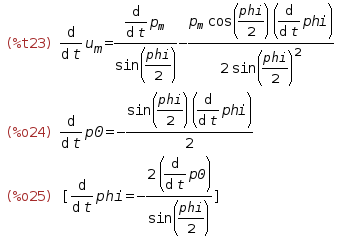
But here we are waited by another nuance. We need to remove the derivatives from the resulting expressions. That is, to remove completely. Because Maxima, when simplifying expressions, does not quite adequately respond to them. For example, if the same derivative is in the expression as a coefficient before the sine in the square and before the cosine in the square of the same angle, while simplifying trigonometry, Maxima does not see the main trigonometric identity in the focus. And if the derivative is replaced by an ordinary expression, it easily collapses the identity into a unit. The same applies to tensor transformations - it’s unwilling to omit indices and collapse with the Levi-Civita tensor if one of the tensors involved in the operation is represented by the time derivative of the other tensor. I haven’t yet met direct indications of a solution to the problem, although I’m looking for them, but for now let's use Crutch Number Two - we will introduce replacements. To begin with, in the expression of the angular velocity, we replace the derivative of the scalar parameter of the quaternion

 dphidt:subst(v0, diff(p0,t), Solv2[1]); 

We perform a direct substitution - the first argument of the function subst() is something to which, it is necessary to replace the expression betrayed by the second argument, in the expression in the third argument. Result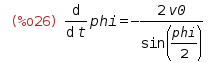

It suits us. Now we substitute this angular velocity into the expression for the derivative of the covort orth of the axis of rotation

 du_mdt:ishow(subst(dphidt, du_mdt))$ 

and perform the replacement of the derivatives of the other quaternion parameters

 du_mdt:ishow(subst(v([m],[]), diff(p([m],[]),t), du_mdt))$ 

well, raise the indices, to obtain the derivative of the contravariant component ort

 durdt:ishow(diff(u([],[r]),t) = contract(expand(rhs(du_mdt)*g([],[r,m]))))$ 

At the output we have a complete set of expressions to perform the substitution.



Well, we carry them out, revealing brackets along the way, forcing Maxima to reduce fractions as much as possible.

 Omega_1:ishow(subst(dphidt, Omega))$ Omega_1:ishow(expand(subst(du_mdt, Omega_1)))$ Omega_1:ishow(expand(subst(durdt, Omega_1)))$ Omega_1:ishow(expand(subst(u_i, Omega_1)))$ Omega_1:ishow(expand(subst(ur, Omega_1)))$ 

The result is already quite decent



but in the second term, the vector product of the vector part of the quaternion itself on itself looms, equal to zero. To SKA removed her use the spell

 Omega_2:ishow(canform(contract(expand(applyb1(Omega_1, lc_l, lc_u)))))$ 

Details of the construction of this command are described by me here . I recall only the meaning - to simplify the tensor expression according to the rules for working with convolutions of the Levi-Civita tensor. The spell removes the zero term



Things are easy - combing trigonometry

 Omega_3:ishow(trigsimp(Omega_2))$ 

and replace the remaining cosine with the quaternion scalar parameter

 Omega_3:ishow(subst(lhs(Lambda0), rhs(Lambda0) , Omega_3))$ 

As a result, we have a rather compact expression.



Print it in LaTeX

 tentex(Omega_3); 

The weather is spoiled by the dumb indices numbered by the function canform() , but here we already handles the indices we need and at the same time we return to the place the derivatives of the Rodrigues-Hamilton parameters



Expression (7) is the long-awaited expression of the angular velocity in terms of the Rodrig – Hamilton parameters. As you can see, it is much more compact than the original expression, written in the parameters of the final rotation. But this is not the only positive feature. Another nice feature will open to us when we get

3. Angular acceleration in the parameters of Rodrig-Hamilton

There are two ways to obtain angular acceleration. The first way, the easiest, to which I, for some reason did not immediately reach, is simply to differentiate (7) by time. It is easily and quickly done manually. The second way I honestly crawled, get the formula in Maxima, simplifying the expression of angular acceleration known to us through the parameters of the final turn



I will demonstrate both ways, I will only take the long way under the spoiler so that my dear reader will not lose the forest for the trees.

So, take the time derivative of (7)



The first term is zero, such as are given up to the mutual annihilation of members, and as a result, without much difficulty, we get





Suddenly, we see a complete analogy with (7), but instead of the first derivatives, there are second derivatives here. The coefficients in the derivatives are the same, which means that the angular velocity and angular acceleration are obtained from the corresponding derived parameters of the Rodrigues-Hamilton multiplication by the same matrix (3 x 4). This, by the way, determined the wide applicability of the quaternionic approach in modeling the motion of spacecraft, and other objects that perform free rotation in space.

Conclusion

The article was published with a focus on working with the Maxima tensor libraries. I can conclude that, even with the described assumptions, it is quite convenient to simplify tensor expressions in it.

And finally, we obtained the expressions of the angular velocity and angular acceleration using the Rodrig – Hamilton orientation parameters convenient for modeling. And they were convinced that formulas (7) and (8) expressing them are not only compact, but also beautiful, in the sense that they use the same linear transformation of parameters to the quaternion to the components of the angular velocity and acceleration vectors. This approach seriously simplifies the organization of modeling programs, in which we still, I hope, will see.

To date, we have come close to examining the dynamics of a free solid body using a tensor apparatus. On account of the next article, I have an interesting idea, which I will try to implement and prepare high-quality material.

Thank you for attention!

To be continued...