Content

1. What is a tensor and what is it for?
2. Vector and tensor operations. Ranks of tensors
3. Curved coordinates
4. Dynamics of a point in the tensor representation
5. Actions on tensors and some other theoretical questions
6. Kinematics of free solid. Nature of angular velocity
7. The final turn of a solid. Rotation tensor properties and method for calculating it
8. On convolutions of the Levi-Civita tensor
9. Conclusion of the angular velocity tensor through the parameters of the final rotation. Apply head and maxima
10. Get the angular velocity vector. We work on the shortcomings
11. Acceleration of the point of the body with free movement. Solid Corner Acceleration
12. Rodrig – Hamilton parameters in solid kinematics
13. SKA Maxima in problems of transformation of tensor expressions. Angular velocity and acceleration in the parameters of Rodrig-Hamilton
14. Non-standard introduction to solid body dynamics
15. Non-free rigid motion
16. Properties of the inertia tensor of a solid
17. Sketch of nut Janibekov
18. Mathematical modeling of the Janibekov effect

Introduction

Finally, we come to a rather interesting topic - the choice of parameters that uniquely determine the orientation of a solid body in space. Historically, the most popular are the angles of rotation - they are primarily mentioned in the classic textbooks of theoretical mechanics.
')

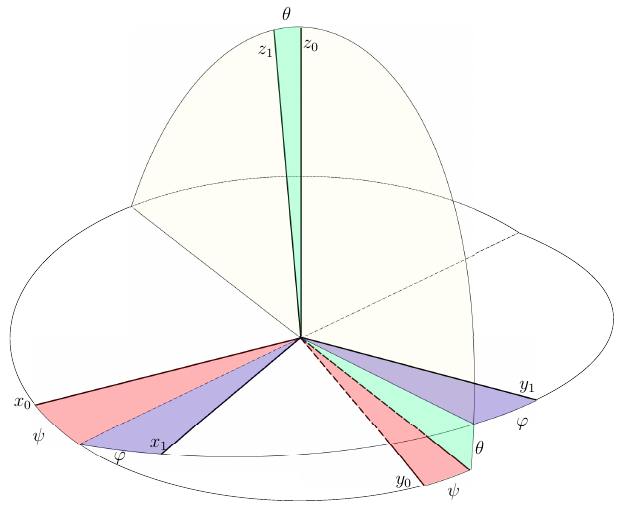
Fig.1. Euler angles are parameters that are familiar to anyone who was involved in computer graphics and modeling of the spatial motion of bodies. And everyone whom they know knows how problematic their use is.


Usually, the rotation angles are used in conjunction with the Cartesian coordinate system, while they say that the associated coordinate system can be combined with the base by three consecutive turns around its axes. Moreover, each next turn is carried out around the axis obtained after the previous turn. In addition, the next turn should not occur around the axis about which the previous turn was made. In this regard, there are 12 different combinations of rotation angles, the most famous of which are Euler angles (Figure 1). Basic coordinate system is rotated around the Z axis (precession angle), then at an angle around the X axis (nutation angle), and again around the Z axis at an angle (angle of own rotation) before combining it with the associated coordinate system.

The use of Euler angles is good for everyone - their number coincides with the number of rotational degrees of freedom of a rigid body, which means they do not generate redundant constraint equations. But, even without resorting to cumbersome formulas, in Figure 1, one can guess where the problem lies.




Fig. 2. Famous Euler kinematic equations. I, in due time, took a sip with them of long and painstaking debugging

There are two values ​​of the nutation angle at which the degeneracy of the Euler kinematic equations occurs (Figure 2) - and . Suppose that the nutation angle took one of these values ​​— then the precession angle and the angle of its own rotation describe the rotation around the same Z axis and are fundamentally indistinguishable from each other. Using the kinematic equations of Euler, we get zero in the denominator and NaN in phase coordinates. Sailed, the integration procedure collapsed.

Another option for turning angles is plane angles: - yaw, - pitch and - roll (picture 3).


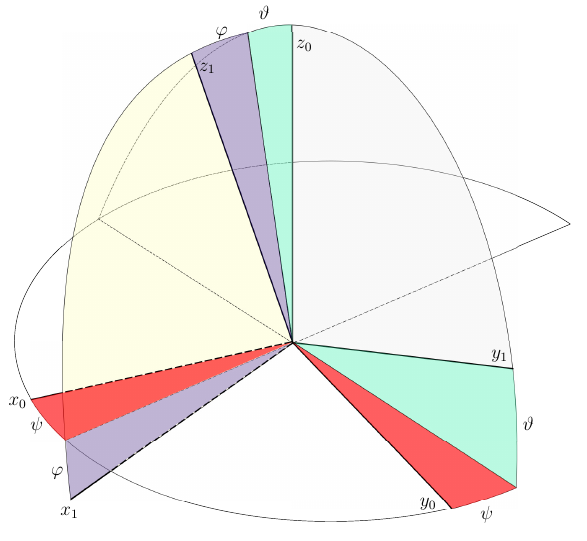
Fig. 3. Aircraft angles - one of the practical ways to determine the orientation of the aircraft in space


These turning parameters degenerate when the pitch , while becoming indistinguishable become heel and yaw. Mature simulators know how crazy the gearbox is when you go to steep pitches.

All possible combinations of angles of rotation have a degeneration. For modeling and laying in the algorithms of orientation control systems, their area of ​​application is limited to critical parameter values. In the last article, we showed that the final rotation parameters are not suitable, and the use of the components of the rotation tensor is impeded by the excessively deep dependencies between them, which gives rise to a high order of the system of equations of motion.

However, the great Leonard Euler introduced into consideration four parameters that do not have degeneration. The then scientific world did not pay special attention to its publication on this issue. This idea, independently of Euler, was developed by Olide Rodrigue, and in the works of William Hamilton received a final theoretical justification. Meet -

1. Quaternions and actions on them

Quaternion is the number of the form



Where called quaternion components. The numbers themselves (1) form the set of hypercomplex numbers including all valid numbers and set of complex numbers . Mathematicians of the era, when Hamilton worked, already knew about complex numbers and how methods built on their basis allow us to solve planimetry problems and it was natural to want to extend the concept of a complex number to apply similar methods to spatial problems. The problem was that adding a second imaginary unit did not solve the problem. Hamilton had the idea that such extended complex numbers may not be three-, but four-component. Working in this direction, in a rush of inspiration on one of his walks, he derived the rule of multiplying such numbers, which finally put together a mosaic of the newborn theory.

So, the multiplication of quaternions is reduced to the algebraic operation of multiplying the sums, with the only difference being that it is required to determine the rules for multiplying imaginary units. Traditionally, each of the imaginary units squared gives -1



and their pairwise works are well described by the diagram.


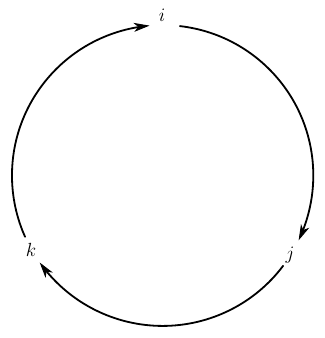
Fig. 4. Multiplication diagram of imaginary units in a quaternion


the meaning of which is simple - if you multiply pairs of imaginary units in the order indicated by the arrow, you get the third imaginary unit with the "+" sign. If the order of multiplication is reversed, the third imaginary unit with a "-" will be obtained. Does not resemble the rule of vector multiplication of orts in Cartesian coordinates? This is it, that is, we get



Using these rules we multiply two quaternions



Wow! Not weak, but we boldly quote similar terms.



and, well, surely you see here painfully familiar actions on vectors. Let our vectors be given



then each quaternion can be represented by a scalar-vector pair



and the result of their multiplication



It is not difficult to simply compare this formula with the result of the multiplication that we have performed, while considering the imaginary units as the ortami of the Cartesian basis. Thus, quaternions include both vectors of three-dimensional space, and for example, quaternions of the form and , will be scalars, and their product is equivalent to the product of scalar values



And the quaternions of the form and are called vector quaternions, and their product



gives a scalar, with a minus sign, and the vector product of the vectors making them.

Due to the presence of the product of vector multiplication, the multiplication operation of quaternions is not commutative



Well, is it necessary to say that by zeroing the last two coefficients of each of the quaternions we get the product of complex numbers? I think it is not worth it, because we are not immersed in a complex area, and if we are talking about complex numbers, then where it is required.

I will not begin to say that adding quaternions and multiplying them by a number is similar to the corresponding operations in the complex field. But what should I talk about, so about the conjugation of quaternion



about the associated norm calculation operation



and operations for calculating the inverse quaternion



And one more useful property concerning the conjugation of the product of quaternions



In addition, the norm of the inverse quaternion is the reciprocal of the norm of the original



These operations are directly related to the fact that today we use hypercomplex numbers.

2. Quaternion as a linear rotation operator

Now let's look at this trick. Let be - one quaternion, and - another quaternion. Let us prove a small theorem

View conversion does not change quaternion norms .

This statement is verified by direct calculation.



Indeed, the quaternion norm does not change with such a transformation. And if the quaternion will be a vector quaternion, then the norm of the vector by which it is determined does not change. That is, the described transformation over the vector does not change its length, it will be orthogonal, or a rotation transformation! The matter is small - to find out which axis and at which angle the rotation occurs, determined by a specific quaternion. To do this, take (for us, no one bothers to do that) and imagine a quaternion as



The value in parentheses is called the monogram (not to be confused with the tensor!) Of the quaternion. We exercise on its vector part



No one bothers to do equivalent transformations to us, so we make them. Now we introduce a replacement



On what basis? Yes, the fact that the sum of squares of these quantities always gives one, and if this is the case, then no one bothers to present these values ​​as the sine and cosine of a certain angle. Why divide the angle by two? We so want, then it will be useful to us, because the angle can be arbitrary. Based on the introduced replacement, we can rewrite the quaternion in the form



Note that the vector , introduced by us, is singular, since



On top of that, let's allow ourselves another assumption - let the quaternion be a single, that is,



Now accurately perform the orthogonal transformation over the vector quaternion



Now multiply the result (2) by the inverse quaternion



In order not to overload the text with “crocodiles”, we will calculate scalar separately.



and the vector part



conversion result. Finally, on the basis of formulas (3) and (4), having carried out not complicated trigonometric simplifications, we come to the conclusion that the output is some vector



So this is ... Rodrig's final turn formula! It turns out that the transformation



which, given that for a single quaternion, the operation of calculating the inverse quaternion is equivalent to conjugation, can be rewritten as



is equivalent to rotating the vector around the axis defined by the ort at an angle . The rotation angle and the vector around which rotation takes place can be calculated from the components of the quaternion, based on the substitutions introduced by us above.

findings

We have seen that the unit quaternion, whose components are constructed by the formulas



determines the final turn. The four parameters that we have quoted are the very parameters of Rodrigues-Hamilton, which uniquely determine the orientation of a solid body in space and do not degenerate at any parameters of rotation. For example, if we zero the rotation angle, then the orth of the rotation axis will also be equal to zero. When turning at any end angle, we can always calculate the position of the axis of rotation.

Well, in the meantime outside the window it dawned ... The plan of this article was somewhat different, and we did not say a word about tensors. Yes, it is for the better, but now we have a clear idea that we will use it for further cunning orientation parameters.

Thank you for attention!

To be continued...