About Burali-Forti, Poincaré and the very definition of a unit
If you, my dear reader, tend to spend a lot of time on the Internet, you've probably already seen this picture with a quote:

Surely you also wondered: what the hell is written here? The formula of this quotation is interesting because a person who has a higher mathematical education, this question arises just as inexorably as a curious seventh-grader. Non-cognitive seventh graders have a slightly different circle of interests that goes beyond the scope of this article; however, even they will not deny themselves the pleasure of giggling at “these crazy nerds”, or as it is formulated there in modern youth slang.
')
In the following text, I will reveal to you the secret of this mysterious combination of characters. Come under the cat, but remember the instructive story about the curious Barbara, who was told about the Banach-Tarski paradox at the market, why she went crazy, cut her nose into a finite number of parts and glued them to the horned sphere of Alexander.
If you are not interested in historical background, feel free to skip to the next section .
So, before us is a quote from the text of an unnamed author, who quotes Poincare, who quotes, in turn, a certain Burali-Forti. To understand all this postmodernism, let's start with the author of the top-level quotation. His name is Victor Filippovich Zhuravlev, he is a doctor of physical and mathematical sciences, a professor, an academician of the Russian Academy of Sciences, and the author of a book under the unshaken name "Fundamentals of Theoretical Mechanics." It is in it, on page number eight (if you look at the 2008 edition), and the above formula is encountered. I will cite here a little context so that it becomes clear to what it is.
Who is Poincare, I suppose, no need to explain. In the light of recent events, even terry humanities should remember this last name in combination with the word "hypothesis" and another last name "Perelman". Very briefly (for those who, from the middle of the nineteenth century until the present moment, sat in a stone bag), Jules Henri Poincaré is one of the greatest mathematicians of all time, an encyclopedic scientist, creator of topology, the mathematical foundations of the theory of relativity, and all sorts of funny and useful things . This quote-in-quote was borrowed from his work Science and Method, 1910 edition. This work is a collection of essays on various mathematical, scientific, philosophical and didactic topics. Very curious, easy to read and still relevant thing that can be pulled apart for quotes a little less than full.
However, we are interested in one specific quote. It is located in the “Mathematics and Logic” chapter, which begins like this:
I suppose the reader has already understood what will be discussed further. With some vehemence, Poincare attacks the mathematicians of the "new school" with their incomprehensible designations and the revision of the foundations. As subsequent events showed, in this matter he turned out to be a retrograd - however, he had good reasons for that. What happened in mathematics in the harsh 1890s could also overwhelm a more indifferent person than this enthusiastic Frenchman.
So we got to the end of the chain, to a quote that does not contain internal quotes. Its author is Cesare Burali-Forti, a mathematician not only great, but who managed to write his name in history thanks to a certain paradox, to which we will return later. The information about him is rather scarce, I could not even find how stress is in his last name. The formula that inspired me to write this article was contained in his article “The Question of Transfinite Numbers”. I found this article in the book by Jean van Heyenort - by the way, the famous Trotskyist - entitled “From Frege To Gödel: A Source Book in Mathematical Logic” (hereinafter I do not dare to translate the names, since May English is from Veri vell notes). It was a great success, because along with her, the book contained Peano’s article “The principles of arithmetic, presented by a new method”. It was in this article that the very “notation that only a few initiates understand” were introduced, without which the Burali-Forte article would be for me just the same as in Chinese.
If you do not want to look at funny quackers, you can skip ahead to the next section.
Before the articles of Peano and Burali-Forti, in the collection book of van Heyenort, there was an article by Frege entitled “The Calculus of Concepts, or the Formal Language of Pure Thought imitating arithmetic”. Friedrich Ludwig Gottlob Frege, a mathematician and philosopher, may, in principle, be considered the creator of the predicate calculus. He has a rather mediated attitude to the topic of this habrapost (Poincaré did not even mention it in his book, although it was Frege who essentially brewed all this mess with the reduction of mathematics to logic). However, I just could not share his most fashionable designations. Fortunately (or unfortunately), they did not take root in modern mathematics because of their complexity. Frege stated, of course, that “the convenience of a typesetter in a printing house is definitely not the highest good,” however, as we can see, this factor also played a certain role. However, enough prefaces.
Of course, it must be admitted that for a person who is far from “this is all,” the modern writing of predicate logic formulas looks a little more clear.
If you know what ordinal numbers are and what the Burali-Forti paradox is, you can go directly to the final section .
German mathematician Georg Cantor - one of the first who began to understand the varieties of infinity. Before him, there were only two of these varieties - potential infinity and actual infinity . You can explain these concepts as follows:
Up to a certain point in mathematics, only potential infinity was encountered, and only theologians operated on current infinity to describe various categories of the divine. Cantor, by roughly introducing current infinity into mathematics, caused a wave of indignation among both religious figures and contemporaries, including the aforementioned Poincare. Moreover, upon careful examination it turned out that the actual infinities are different. The number of natural numbers is one infinity, the number of real numbers is another, and the second infinity is greater than the first. And the number of functions of a valid argument is the third infinity, surpassing the first two together!
Natural numbers are used to denote finite quantities, but what to do with infinite quantities? For this, the natural series has been expanded to a set of so-called cardinal numbers . A cardinal number is the number (in the broad sense of the word) of elements of a certain set. Unit - the number of elements in the set of one element. Two - the number of elements in the set of two elements. Further, behind the natural numbers, looms the number N 0 , equal to the number of natural numbers. In general, instead of the letter N, there should be a Hebrew letter “Alef”, but when I tried to insert the corresponding Unicode character, the text direction changed from “right to left” from myears , and I didn't understand how to return it to its original state, spat.
So, for N 0 should be some N 1 , but the question of how many it corresponds to, turned out to be non-trivial (see Continuum Hypothesis ). With the notion of “the next number”, a hitch occurred during the transition from finite to infinite.
There are, however, other "infinite numbers" - the so-called ordinal numbers , they are also ordinals , also invented by Cantor. Their definition is quite difficult, but I will try to outline it in a few words. If cardinal numbers correspond to simple sets, then ordinals correspond to ordered sets, i.e. such that for any of their two elements indicated. which one is more and which one is less. The order relation must meet some obvious criteria, which we will modestly keep silent about. In addition, for constructing ordinals on an ordered set, additional conditions are imposed under which it is called completely ordered . If one can establish a one-to-one correspondence between two completely ordered sets, preserving the order relation, then these sets have the same ordinal.
Finite ordinals can be put in correspondence to natural numbers. For example, the ordinal of the set {1, 2, 3} can be assigned to a natural number 3. Ordinals can be added together, and in the case of finite ordinals, the addition will be consistent with the addition of natural numbers (for example, Ord {1, 2} + Ord {1 , 2, 3} = Ord {1, 2, 3, 4, 5}). To add two ordinals, you need to take the corresponding sets, and then combine them into one set and set the following order relation on it:
The ordinal of such a set will be the sum of ordinals. Thus, there are no problems with the definition of the next ordinal: you just need to take the previous ordinal and add the ordinal 1 to it.
The ordinal of the set of natural numbers is denoted by ω. It is followed by the ordinal ω + 1. It corresponds to the set of natural numbers, to which was added the “last” number greater than any other. Then comes the ordinal ω + 2 - it corresponds to the natural series with the "last" and "last but one" number. There are also ordinals such as 2ω (natural series followed by another natural series), 3ω, 4ω, ω 2 , ω ω ...
As you can see, Cantor was a great entertainer. Ironically, it was the ordinal numbers that marked the beginning of the end of his theory, which would later be called "the naive theory of sets." Using ordinal numbers, Burali-Forti came to a paradox. The course of his reasoning was something like this: take a set of ordinals and prove that it is completely orderly. So, he himself corresponds to some ordinal. Let us prove that this ordinal is greater than or equal to any other ordinal. Now let's add one to it. Let's make surprised eyes.
Now, armed with knowledge and enthusiasm, we are ready to go to the point and figure out what the formula really means at the very beginning of the habpost, far, far above.
To understand the notation of Burali-Forti was not easy. To the notation introduced by Peano, he added a number of his own notation. Unlike Peano, he did not begin to describe in detail his innovations at the beginning of the article. Perhaps these descriptions are contained elsewhere, but, unfortunately (or fortunately), I could not find the complete collection of Burali-Forti on the Internet. Therefore, in a couple of places I had to think out the meaning based on the context. This process was like solving a famous NSA puzzle .
To begin with, Poincare (and then Zhuravlev) gives a not quite correct formula. In the original, it looks like this:

Pay attention to the two overlays, their presence is important.
The letter "epsilon" here means belonging, it is from it that the modern sign "" "originated. Un is the set of all sets containing exactly one element. Accordingly, the entry "u ε Un" means only that u is a set with one element. Such a non-trivial notation, apparently, is caused by the fact that it has not yet been accepted to “construct” a set of individual elements with the help of the record u = {a, b, c ...}.
The Burali-Forti overline replaces the square brackets, entered by Peano as an "inversion sign." Peano used it in a fairly wide range of cases. For example, b [+ a] it meant ba, the expression [sin] (x) symbolized arcsin (x). The record [x ε] (a certain condition) meant a set of X's satisfying this condition. Thus, the notation [(u, v) ε] (u ε Un) means “the set of such pairs (u, v) such that u is a set of one element”. I, perhaps, will use the Peano notation, since I don’t see a convenient way to make an overline in the habra editor.
Ko is a set of ordered sets. Burali-Forti ordered sets are defined as pairs (set, order relation). Consequently, the notation {Ko ⋂ [(u, v) ε] (u ε Un)} means simply “the set of ordered single-element sets”.
Using a combination of characters "T '" Burali Forte means the operation of taking the ordinal. More strictly: the expression T '(u, v) means the ordinal of the set u, on which the relation of order v is given. Here, however, there is some discrepancy: in the formula in question, the function T 'is not applied to the pair (set, order relation), but to the set of such pairs. Based on the context, I can only assume that there is some agreement under which in such cases the function is applied to each element, and the output is a set consisting of its values for all elements. With this reading, T '{Ko ⋂ [(u, v) ε] (u ε Un)} is the set of ordinals of all singleton ordered sets. Since all one-element ordered sets are equivalent, this set of ordinals will contain only one element — the ordinal unit.
As for the squiggle with a dash, with her understanding, I had the most problems. I had to look for other works of Burali-Forti. In one of them, “Logica Matematica” (apparently, some textbook, but I’m not completely sure, because it was written in Italian) I found the function L (there was a lowercase “l”, but it’s too much like a wand, because for clarity, I will use the title). It works as follows: it takes its argument and transforms it into a set, the only element of which is this very argument. In modern notation: L (x) = {x}.
If you identify the squiggle as L, and the dash as inversion, it turns out that [L] is an inverse transformation that extracts its only element from the set. In this case, [L] T '{Ko ⋂ [(u, v) ε] (u ε Un)} is really one. Ordinal unit, but this is the little things.
The next time someone shows you a picture with this formula (and this will happen, this is the Internet), you can tell him what this formula means. More precisely, you can start telling. Hardly he listens to the end. And it will be, in principle, right: this is a completely ordinary, unremarkable formula. In the arguments of Burali-Forti, she did not occupy any central place, but was only a passing point in the formulation of the paradox. All her fault lies in the fact that she caught the eye of Poincare, who saw in her a certain undesirable philosophical meaning, “unfolding clamps”. As for its infernal type, here the Frege designations will give a hundred points of handicap.
Here I would like to place links to the books mentioned, but thanks to the efforts of the right-holders, I had to download them from all sorts of unintelligible places, from suspicious file sharing sites, from the ed2k network ... and interesting reading. “From Frege to Gödel” by van Heyenort is also very curious, but hard to understand and does not seem to exist in Russian.
In the light of recent events (transfer of “iron” hubs to giktimes) I want to conduct a small survey that is not directly related to the topic of habpost. I hope you forgive this liberty.

Surely you also wondered: what the hell is written here? The formula of this quotation is interesting because a person who has a higher mathematical education, this question arises just as inexorably as a curious seventh-grader. Non-cognitive seventh graders have a slightly different circle of interests that goes beyond the scope of this article; however, even they will not deny themselves the pleasure of giggling at “these crazy nerds”, or as it is formulated there in modern youth slang.
')
In the following text, I will reveal to you the secret of this mysterious combination of characters. Come under the cat, but remember the instructive story about the curious Barbara, who was told about the Banach-Tarski paradox at the market, why she went crazy, cut her nose into a finite number of parts and glued them to the horned sphere of Alexander.
Who are all these people?
If you are not interested in historical background, feel free to skip to the next section .
So, before us is a quote from the text of an unnamed author, who quotes Poincare, who quotes, in turn, a certain Burali-Forti. To understand all this postmodernism, let's start with the author of the top-level quotation. His name is Victor Filippovich Zhuravlev, he is a doctor of physical and mathematical sciences, a professor, an academician of the Russian Academy of Sciences, and the author of a book under the unshaken name "Fundamentals of Theoretical Mechanics." It is in it, on page number eight (if you look at the 2008 edition), and the above formula is encountered. I will cite here a little context so that it becomes clear to what it is.
Note that the presentation of any formal axiomatization of classical mechanics in the course of mechanics is inappropriate, since it is in fact the chapter of mathematical logic, and not of mechanics itself.
Similarly, the axiomatization of arithmetic is not the subject of arithmetic itself. <then comes the same quote, I will not reprint it>
So in mechanics, it makes sense to assume that readers have sufficient physical intuition, so as not to overload the presentation of the foundations with excessive formalism.
Who is Poincare, I suppose, no need to explain. In the light of recent events, even terry humanities should remember this last name in combination with the word "hypothesis" and another last name "Perelman". Very briefly (for those who, from the middle of the nineteenth century until the present moment, sat in a stone bag), Jules Henri Poincaré is one of the greatest mathematicians of all time, an encyclopedic scientist, creator of topology, the mathematical foundations of the theory of relativity, and all sorts of funny and useful things . This quote-in-quote was borrowed from his work Science and Method, 1910 edition. This work is a collection of essays on various mathematical, scientific, philosophical and didactic topics. Very curious, easy to read and still relevant thing that can be pulled apart for quotes a little less than full.
For example:
How to explain that many minds refuse to understand mathematics? Is it not paradoxical? Indeed, science, which appeals only to the basic principles of logic, for example, the principle of contradiction, appeals to what constitutes, so to speak, the skeleton of our understanding, to that which cannot be abandoned, without giving up at the same time from thinking itself. , and yet there are people who find this science dark! And most of these people! Let them be unable to invent - this is still acceptable. But they do not understand the evidence that is being offered to them, they remain blind when they are given a light that burns for us with a clear and bright flame — that is extremely strange.
Or on the other hand:
Here in fourth grade. The teacher dictates: "a circle is a geometrical place of points on a plane that are at the same distance from one internal point, called the center." A good student writes this phrase in his notebook; the bad student draws “little men” in it, but neither of them understood anything. Then the teacher takes the chalk and draws a circle on the blackboard. “Aha,” the pupils think, “why he didn’t say right away: the circle is a circle, and we would understand right away.”
However, we are interested in one specific quote. It is located in the “Mathematics and Logic” chapter, which begins like this:
Is it possible to reduce mathematics to logic without first referring to the principles that are peculiar to it, mathematics? There is a school of mathematicians, which with all the passion and faith in the cause seeks to prove it. She developed a special language in which there are no more words, but only signs. This language is understandable only to a few initiates, so that the profane are inclined to bow before the categorical statements of hot adepts.
I suppose the reader has already understood what will be discussed further. With some vehemence, Poincare attacks the mathematicians of the "new school" with their incomprehensible designations and the revision of the foundations. As subsequent events showed, in this matter he turned out to be a retrograd - however, he had good reasons for that. What happened in mathematics in the harsh 1890s could also overwhelm a more indifferent person than this enthusiastic Frenchman.
So we got to the end of the chain, to a quote that does not contain internal quotes. Its author is Cesare Burali-Forti, a mathematician not only great, but who managed to write his name in history thanks to a certain paradox, to which we will return later. The information about him is rather scarce, I could not even find how stress is in his last name. The formula that inspired me to write this article was contained in his article “The Question of Transfinite Numbers”. I found this article in the book by Jean van Heyenort - by the way, the famous Trotskyist - entitled “From Frege To Gödel: A Source Book in Mathematical Logic” (hereinafter I do not dare to translate the names, since May English is from Veri vell notes). It was a great success, because along with her, the book contained Peano’s article “The principles of arithmetic, presented by a new method”. It was in this article that the very “notation that only a few initiates understand” were introduced, without which the Burali-Forte article would be for me just the same as in Chinese.
By the way
a brief retelling of the content of the very article Peano is in one of my habraposts
Lyrical digression
If you do not want to look at funny quackers, you can skip ahead to the next section.
Before the articles of Peano and Burali-Forti, in the collection book of van Heyenort, there was an article by Frege entitled “The Calculus of Concepts, or the Formal Language of Pure Thought imitating arithmetic”. Friedrich Ludwig Gottlob Frege, a mathematician and philosopher, may, in principle, be considered the creator of the predicate calculus. He has a rather mediated attitude to the topic of this habrapost (Poincaré did not even mention it in his book, although it was Frege who essentially brewed all this mess with the reduction of mathematics to logic). However, I just could not share his most fashionable designations. Fortunately (or unfortunately), they did not take root in modern mathematics because of their complexity. Frege stated, of course, that “the convenience of a typesetter in a printing house is definitely not the highest good,” however, as we can see, this factor also played a certain role. However, enough prefaces.
Behold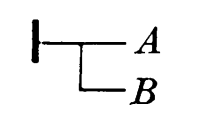
“From A follows B”

“From A follows B, and from this follows G”
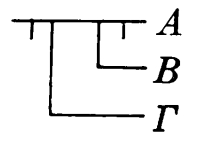
"It is not true that from the fact that the negation of A implies C, it follows G"

"Hell's darkness divided by chthonic horror"

“Ph'nglui mglnnah Cthulhu R'layh vgahnagl fhtagn! Aya Cthulhu, Aya Dagon! ”
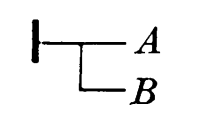
“From A follows B”

“From A follows B, and from this follows G”
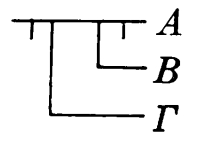
"It is not true that from the fact that the negation of A implies C, it follows G"

"Hell's darkness divided by chthonic horror"

“Ph'nglui mglnnah Cthulhu R'layh vgahnagl fhtagn! Aya Cthulhu, Aya Dagon! ”
Of course, it must be admitted that for a person who is far from “this is all,” the modern writing of predicate logic formulas looks a little more clear.
Theoretical information
If you know what ordinal numbers are and what the Burali-Forti paradox is, you can go directly to the final section .
German mathematician Georg Cantor - one of the first who began to understand the varieties of infinity. Before him, there were only two of these varieties - potential infinity and actual infinity . You can explain these concepts as follows:
- Potential infinity. Suppose we have a bunch of apples, and every day we put another apple there. Sooner or later, the number of apples in a handful will be greater than any pre-set number.
- Actual infinity. Suppose we have a handful in which an infinite number of apples.
Up to a certain point in mathematics, only potential infinity was encountered, and only theologians operated on current infinity to describe various categories of the divine. Cantor, by roughly introducing current infinity into mathematics, caused a wave of indignation among both religious figures and contemporaries, including the aforementioned Poincare. Moreover, upon careful examination it turned out that the actual infinities are different. The number of natural numbers is one infinity, the number of real numbers is another, and the second infinity is greater than the first. And the number of functions of a valid argument is the third infinity, surpassing the first two together!
Natural numbers are used to denote finite quantities, but what to do with infinite quantities? For this, the natural series has been expanded to a set of so-called cardinal numbers . A cardinal number is the number (in the broad sense of the word) of elements of a certain set. Unit - the number of elements in the set of one element. Two - the number of elements in the set of two elements. Further, behind the natural numbers, looms the number N 0 , equal to the number of natural numbers. In general, instead of the letter N, there should be a Hebrew letter “Alef”, but when I tried to insert the corresponding Unicode character, the text direction changed from “right to left” from my
So, for N 0 should be some N 1 , but the question of how many it corresponds to, turned out to be non-trivial (see Continuum Hypothesis ). With the notion of “the next number”, a hitch occurred during the transition from finite to infinite.
There are, however, other "infinite numbers" - the so-called ordinal numbers , they are also ordinals , also invented by Cantor. Their definition is quite difficult, but I will try to outline it in a few words. If cardinal numbers correspond to simple sets, then ordinals correspond to ordered sets, i.e. such that for any of their two elements indicated. which one is more and which one is less. The order relation must meet some obvious criteria, which we will modestly keep silent about. In addition, for constructing ordinals on an ordered set, additional conditions are imposed under which it is called completely ordered . If one can establish a one-to-one correspondence between two completely ordered sets, preserving the order relation, then these sets have the same ordinal.
Finite ordinals can be put in correspondence to natural numbers. For example, the ordinal of the set {1, 2, 3} can be assigned to a natural number 3. Ordinals can be added together, and in the case of finite ordinals, the addition will be consistent with the addition of natural numbers (for example, Ord {1, 2} + Ord {1 , 2, 3} = Ord {1, 2, 3, 4, 5}). To add two ordinals, you need to take the corresponding sets, and then combine them into one set and set the following order relation on it:
- If we compare two elements from the same original set, then we use the order relation that was in that set
- If we compare two elements from different source sets, then the element from the second set is always greater
The ordinal of such a set will be the sum of ordinals. Thus, there are no problems with the definition of the next ordinal: you just need to take the previous ordinal and add the ordinal 1 to it.
The ordinal of the set of natural numbers is denoted by ω. It is followed by the ordinal ω + 1. It corresponds to the set of natural numbers, to which was added the “last” number greater than any other. Then comes the ordinal ω + 2 - it corresponds to the natural series with the "last" and "last but one" number. There are also ordinals such as 2ω (natural series followed by another natural series), 3ω, 4ω, ω 2 , ω ω ...
As you can see, Cantor was a great entertainer. Ironically, it was the ordinal numbers that marked the beginning of the end of his theory, which would later be called "the naive theory of sets." Using ordinal numbers, Burali-Forti came to a paradox. The course of his reasoning was something like this: take a set of ordinals and prove that it is completely orderly. So, he himself corresponds to some ordinal. Let us prove that this ordinal is greater than or equal to any other ordinal. Now let's add one to it. Let's make surprised eyes.
Now, armed with knowledge and enthusiasm, we are ready to go to the point and figure out what the formula really means at the very beginning of the habpost, far, far above.
The essence
To understand the notation of Burali-Forti was not easy. To the notation introduced by Peano, he added a number of his own notation. Unlike Peano, he did not begin to describe in detail his innovations at the beginning of the article. Perhaps these descriptions are contained elsewhere, but, unfortunately (or fortunately), I could not find the complete collection of Burali-Forti on the Internet. Therefore, in a couple of places I had to think out the meaning based on the context. This process was like solving a famous NSA puzzle .
To begin with, Poincare (and then Zhuravlev) gives a not quite correct formula. In the original, it looks like this:

Pay attention to the two overlays, their presence is important.
The letter "epsilon" here means belonging, it is from it that the modern sign "" "originated. Un is the set of all sets containing exactly one element. Accordingly, the entry "u ε Un" means only that u is a set with one element. Such a non-trivial notation, apparently, is caused by the fact that it has not yet been accepted to “construct” a set of individual elements with the help of the record u = {a, b, c ...}.
The Burali-Forti overline replaces the square brackets, entered by Peano as an "inversion sign." Peano used it in a fairly wide range of cases. For example, b [+ a] it meant ba, the expression [sin] (x) symbolized arcsin (x). The record [x ε] (a certain condition) meant a set of X's satisfying this condition. Thus, the notation [(u, v) ε] (u ε Un) means “the set of such pairs (u, v) such that u is a set of one element”. I, perhaps, will use the Peano notation, since I don’t see a convenient way to make an overline in the habra editor.
Ko is a set of ordered sets. Burali-Forti ordered sets are defined as pairs (set, order relation). Consequently, the notation {Ko ⋂ [(u, v) ε] (u ε Un)} means simply “the set of ordered single-element sets”.
Using a combination of characters "T '" Burali Forte means the operation of taking the ordinal. More strictly: the expression T '(u, v) means the ordinal of the set u, on which the relation of order v is given. Here, however, there is some discrepancy: in the formula in question, the function T 'is not applied to the pair (set, order relation), but to the set of such pairs. Based on the context, I can only assume that there is some agreement under which in such cases the function is applied to each element, and the output is a set consisting of its values for all elements. With this reading, T '{Ko ⋂ [(u, v) ε] (u ε Un)} is the set of ordinals of all singleton ordered sets. Since all one-element ordered sets are equivalent, this set of ordinals will contain only one element — the ordinal unit.
As for the squiggle with a dash, with her understanding, I had the most problems. I had to look for other works of Burali-Forti. In one of them, “Logica Matematica” (apparently, some textbook, but I’m not completely sure, because it was written in Italian) I found the function L (there was a lowercase “l”, but it’s too much like a wand, because for clarity, I will use the title). It works as follows: it takes its argument and transforms it into a set, the only element of which is this very argument. In modern notation: L (x) = {x}.
If you identify the squiggle as L, and the dash as inversion, it turns out that [L] is an inverse transformation that extracts its only element from the set. In this case, [L] T '{Ko ⋂ [(u, v) ε] (u ε Un)} is really one. Ordinal unit, but this is the little things.
The next time someone shows you a picture with this formula (and this will happen, this is the Internet), you can tell him what this formula means. More precisely, you can start telling. Hardly he listens to the end. And it will be, in principle, right: this is a completely ordinary, unremarkable formula. In the arguments of Burali-Forti, she did not occupy any central place, but was only a passing point in the formulation of the paradox. All her fault lies in the fact that she caught the eye of Poincare, who saw in her a certain undesirable philosophical meaning, “unfolding clamps”. As for its infernal type, here the Frege designations will give a hundred points of handicap.
Bibliography
Here I would like to place links to the books mentioned, but thanks to the efforts of the right-holders, I had to download them from all sorts of unintelligible places, from suspicious file sharing sites, from the ed2k network ... and interesting reading. “From Frege to Gödel” by van Heyenort is also very curious, but hard to understand and does not seem to exist in Russian.
Post Scriptum
In the light of recent events (transfer of “iron” hubs to giktimes) I want to conduct a small survey that is not directly related to the topic of habpost. I hope you forgive this liberty.
Source: https://habr.com/ru/post/263067/
All Articles