Insert in the middle: ArrayList vs. LinkedList
Somehow during the interview I was asked the question: which list implementation would insert in the middle faster: ArrayList or LinkedList? At first glance, the question is simple - you need to calculate the algorithmic complexity of each option and compare them. The insert in the middle can be divided into two operations: the search for the middle of the list and the insert itself. For ArrayList, searching for an element by index is not difficult, since the elements of the list are in an array. Algorithmic complexity is O (1). In the case of LinkedList, you will have to iterate through all the elements sequentially, until we get to the desired element. The complexity will be O (n). Insertion in ArrayList is connected with the shift of all elements that are after the insertion point, therefore the algorithmic complexity of this operation is O (n). In LinkedList, insertion consists in creating a new binding object and setting references to it from neighboring elements. O (1) complexity. In sum, the complexity of insertion in the middle of ArrayList and LinkedList is the same - O (n). I showed the reasoning to the interviewer, to which he asked me a question: “So, is it still faster: run through the elements or shift the elements?”. I quickly figured out that the read operation is in fact faster than the write operation, said LinkedList will cope faster.
When I came home, I thought about this issue. I looked for a solution to this problem on the forums. Someone agreed with me, but many people took into account that the offset operation is performed by a native method that works faster, so ArrayList will insert it in the middle faster. Not having received a final and irrefutable answer, I decided to conduct my own research.
At first I went deep into studying the source code of these classes. Inserting an element into an ArrayList goes like this: first, if necessary, the array is enlarged, then all elements after the insertion point are shifted by the number of positions equal to the number of inserted elements (I consider one element), and at the end the inserted element is replaced. The array increases at a rate of n * 1.5, where n is the size of the array, and the minimum increase under standard conditions (capacity = 10) is 5 elements. In this regard, the operation to increase the array in the calculation of the algorithmic complexity of the insert can be neglected. The shift of elements located after the insertion point has an algorithmic complexity O (n). Thus, the total complexity still remains O (n). Yes, we keep in mind that the operation of increasing the array slightly increases the complexity, but the nativity of actions with an array increases the speed of work.
A search for an item in LinkedList starts in a loop from the edge of the list. If the item you are looking for is in the first half of the list, then the search is from the beginning, otherwise it is from the end. Since we insert it in the middle, we will pass exactly half of the elements in the cycle. The complexity is O (n). The insert itself, as I wrote above, is to create an object and specify references to it. O (1) complexity. Again, I did not find out anything new: the total complexity remained O (n), while keeping in mind that the creation of an object is an “expensive” operation.
')
Analysis of the source code did not clarify the situation, so I began to write tests. I decided to investigate the dependence on two parameters: the initial size of the list and the number of inserts in a row (the number of iterations).
For each size of the list and the number of iterations, one ArrayList and LinkedList are created, they are filled with the same objects, after which n insertions of one object into the middle are taken for measuring the speed. As a comparison value, I use the logarithm decimal from the ratio of the execution times of ArrayList to LinkedList. When this value is less than zero, ArrayList does it faster, when more - faster LinkedList.
I give the test results in the table:
And in the chart:

On the X axis, the initial size of the list is indicated, lines represent different numbers of iterations, and on the Y axis, the ratio of the speed of the two list implementations.
Since the list size increases with each iteration, you can make a general conclusion: LinkList works faster with a small list size. But the most important thing: without a clear specification of the conditions, the speed of operation of these two algorithms cannot be compared!
To increase the accuracy, I abandoned the parameter for the number of inserts and reduced the size step to one. For each of the sizes I ran the test a thousand times and took the average. Got a schedule:
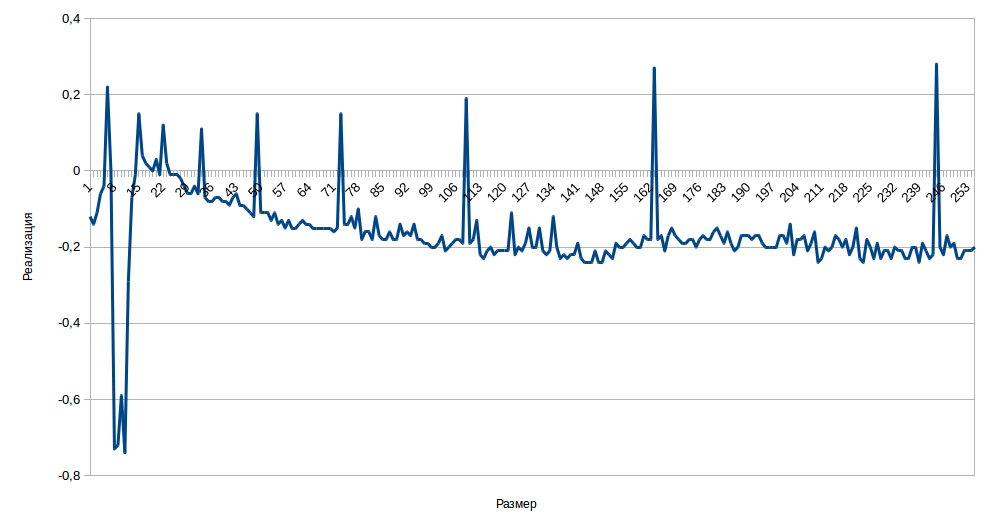
The graph is pronounced bursts. They are located exactly at the places where ArrayList produces an increase in the array. Therefore, it can be said that it is impossible to neglect this operation, as I considered at the beginning, analyzing the source code.
The general conclusion can be drawn as follows: the insert operation in the middle occurs mostly faster in ArrayList, but not always. From a theoretical point of view, it is impossible to unambiguously compare the speed of these two algorithms without taking into account the initial size of the list.
Thank you for your attention, I hope someone will find my work interesting and / or useful.
When I came home, I thought about this issue. I looked for a solution to this problem on the forums. Someone agreed with me, but many people took into account that the offset operation is performed by a native method that works faster, so ArrayList will insert it in the middle faster. Not having received a final and irrefutable answer, I decided to conduct my own research.
At first I went deep into studying the source code of these classes. Inserting an element into an ArrayList goes like this: first, if necessary, the array is enlarged, then all elements after the insertion point are shifted by the number of positions equal to the number of inserted elements (I consider one element), and at the end the inserted element is replaced. The array increases at a rate of n * 1.5, where n is the size of the array, and the minimum increase under standard conditions (capacity = 10) is 5 elements. In this regard, the operation to increase the array in the calculation of the algorithmic complexity of the insert can be neglected. The shift of elements located after the insertion point has an algorithmic complexity O (n). Thus, the total complexity still remains O (n). Yes, we keep in mind that the operation of increasing the array slightly increases the complexity, but the nativity of actions with an array increases the speed of work.
A search for an item in LinkedList starts in a loop from the edge of the list. If the item you are looking for is in the first half of the list, then the search is from the beginning, otherwise it is from the end. Since we insert it in the middle, we will pass exactly half of the elements in the cycle. The complexity is O (n). The insert itself, as I wrote above, is to create an object and specify references to it. O (1) complexity. Again, I did not find out anything new: the total complexity remained O (n), while keeping in mind that the creation of an object is an “expensive” operation.
')
Analysis of the source code did not clarify the situation, so I began to write tests. I decided to investigate the dependence on two parameters: the initial size of the list and the number of inserts in a row (the number of iterations).
Sample Source Code
package com.jonasasx.liststest; import java.util.ArrayList; import java.util.LinkedList; import java.util.List; public class Main { private static final int MAX_SIZE = 1000; private static final int MAX_ITERATIONS = 10000; private static final float STEP_SIZE = 2f; private static final float STEP_ITERATIONS = 5; private static final int TESTS_COUNT = 100; public static void main(String[] args) throws InterruptedException { ArrayList<String> arrayList; LinkedList<String> linkedList; for (float size = 1; size < MAX_SIZE; size *= STEP_SIZE) { for (float iterations = 1; iterations < MAX_ITERATIONS; iterations *= STEP_ITERATIONS) { double sum = 0; for (int k = 0; k < TESTS_COUNT; k++) { arrayList = new ArrayList<>(); linkedList = new LinkedList<>(); fillList(arrayList, (int) size); fillList(linkedList, (int) size); sum += Math.log10(calculateRatio(arrayList, linkedList, (int) iterations)); } double logRatio = sum / TESTS_COUNT; System.out.println(String.format("%07d\t%07d\t%07.2f\t%s", (int) size, (int) iterations, logRatio, logRatio > 0 ? "Linked" : "Array")); } System.out.println(); } } static void fillList(List<String> list, int size) { for (int i = 0; i < size; i++) { list.add("0"); } } static double calculateRatio(ArrayList<String> arrayList, LinkedList<String> linkedList, int iterations) { long l1 = calculateAL(arrayList, iterations); long l2 = calculateLL(linkedList, iterations); if (l1 == 0 || l2 == 0) throw new java.lang.IllegalStateException(); return (double) l1 / (double) l2; } static long calculateAL(ArrayList<String> list, int m) { long t = System.nanoTime(); for (int i = 0; i < m; i++) { list.add(list.size() / 2, "0"); } return System.nanoTime() - t; } static long calculateLL(LinkedList<String> list, int m) { long t = System.nanoTime(); for (int i = 0; i < m; i++) { list.add(list.size() / 2, "0"); } return System.nanoTime() - t; } } For each size of the list and the number of iterations, one ArrayList and LinkedList are created, they are filled with the same objects, after which n insertions of one object into the middle are taken for measuring the speed. As a comparison value, I use the logarithm decimal from the ratio of the execution times of ArrayList to LinkedList. When this value is less than zero, ArrayList does it faster, when more - faster LinkedList.
I give the test results in the table:
| Iterations | |||||||||||
| The size | one | 2 | four | eight | sixteen | 32 | 64 | 128 | 256 | 512 | |
| one | -0.12 | 0.01 | -0.04 | 0.01 | 0.03 | -0.04 | -0.09 | -0.19 | -0.21 | -0.31 | |
| five | -0,14 | 0.02 | -0.02 | 0.07 | -0,08 | 0 | -0.15 | -0.31 | -0,42 | -0,52 | |
| 25 | -0.12 | 0.2 | 0.19 | 0.13 | 0.07 | 0.04 | -0,1 | -0.29 | -0.47 | -0,56 | |
| 125 | -0.31 | -0.01 | 0.01 | 0 | -0.03 | -0.11 | -0.17 | -0.35 | -0.48 | -0.57 | |
| 625 | -0.47 | -0.49 | -0.48 | -0.45 | -0.49 | -0,51 | -0,53 | -0.6 | -0.67 | -0.78 |
And in the chart:

On the X axis, the initial size of the list is indicated, lines represent different numbers of iterations, and on the Y axis, the ratio of the speed of the two list implementations.
Since the list size increases with each iteration, you can make a general conclusion: LinkList works faster with a small list size. But the most important thing: without a clear specification of the conditions, the speed of operation of these two algorithms cannot be compared!
To increase the accuracy, I abandoned the parameter for the number of inserts and reduced the size step to one. For each of the sizes I ran the test a thousand times and took the average. Got a schedule:

The graph is pronounced bursts. They are located exactly at the places where ArrayList produces an increase in the array. Therefore, it can be said that it is impossible to neglect this operation, as I considered at the beginning, analyzing the source code.
The general conclusion can be drawn as follows: the insert operation in the middle occurs mostly faster in ArrayList, but not always. From a theoretical point of view, it is impossible to unambiguously compare the speed of these two algorithms without taking into account the initial size of the list.
Thank you for your attention, I hope someone will find my work interesting and / or useful.
Source: https://habr.com/ru/post/262943/
All Articles