10+ tips on writing fast code in Mathematica
Translation of the post by John McLune (Jon McLoone) " 10 Tips for Writing Fast Mathematica Code ".
Many thanks to Kirill Guzenko KirillGuzenko for help with the translation.
The post of John McLune talks about common techniques for speeding up code written in the Wolfram Language. For those interested in this issue, we recommend that you familiarize yourself with the video “Optimizing Code in Wolfram Mathematica”, from which you will learn in detail and many interesting examples about code optimization techniques, both discussed in the article (but in more detail) and others.
When people tell me that Mathematica is not fast enough, I usually ask you to look at the code and often discover that the problem is not Mathematica performance, but not optimal use. I would like to share a list of things that I pay attention to first of all when I try to optimize the code in Mathematica .
The most common mistake that I notice when I deal with slow code is setting too high a precision for a given task. Yes, inappropriate use of exact symbolic arithmetic is the most common case.
Most computational software systems have no such thing as exact arithmetic — for them, 1/3 is the same as 0.33333333333333. This difference can play a big role when you are faced with complex and unstable tasks, however for most tasks the floating-point numbers fully satisfy the needs, and what is important - the calculations with them are much faster. In Mathematica, any number with a dot and with less than 16 digits is automatically processed with machine precision, so you should always use a decimal point if speed is more important than precision in this task (for example, enter a third as 1./3.). Here is a simple example where working with floating-point numbers is almost 50.6 times faster than working with exact numbers, which will only be converted to floating-point numbers. And in this case the same result is obtained.
')
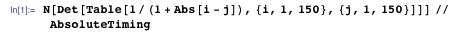


The same can be said for symbolic calculations. If the symbolic form of the answer is not important for you and the stability in this task does not play a special role, then try as soon as possible to proceed to the form of a floating-point number. For example, solving this polynomial equation in symbolic form, before substituting values, Mathematica builds an intermediate symbolic solution of five pages.


But if you do the substitution first, Solve will use much faster numerical methods.


When working with data lists, you should be consistent in the use of real numbers. Just one exact value in the data set will translate it into a more flexible, but less efficient form.




The Compile function accepts Mathematica code and allows you to pre-set the types (real, complex, etc.) and structures (value, list, matrix, etc.) of the input arguments. This deprives parts of the Mathematica language of flexibility, but frees it from having to worry about, “What if the argument is in symbolic form?” And other such things. Mathematica can optimize the program and create a bytecode to run it on its virtual machine (compilation in C is also possible - see below). Not everything can be compiled, and a very simple code may not get any advantages, however complex and low-level computational code can get really big acceleration.
Here is an example:




Using Compile instead of Function gives acceleration more than 80 times.



But we can go further by telling Compile about the possibility of parallelizing this code, getting even better results.



On my dual-core machine, I got a result 150 times faster than in the original case; The speed increase will be even more noticeable with a large number of cores.
However, it should be remembered that many functions in Mathematica , such as Table , Plot , NIntegrate, and some more automatically compile their arguments, so that you will not see any improvements when using Compile for your code.
In addition, if your code is compiled, you can also use the CompilationTarget -> “C” option to generate C code, which automatically causes the C compiler to compile into a DLL and send a link to it in Mathematica . We have additional costs at the compilation stage, but the DLL is executed directly in the processor and not in the Mathematica virtual machine, so the results can be even faster (in our case, 450 times faster than the original code).



Mathematica contains many features. More than an ordinary person can learn in one go (the latest version of Mathematica 10.2 already contains more than 5000 functions). So it is not surprising that I often see code where someone implements some operations, not knowing that Mathematica already knows how to implement them. And this is not only a waste of time for the invention of the bicycle; Our guys have worked hard to create and most effectively implement the best algorithms for various types of input data, so the built-in functions work really fast.
If you find something similar, but not quite, then you should check the parameters and optional arguments - they often generalize functions and cover many special and more distant applications.
Here is an example. If I have a list of a million 2x2 matrices that I want to turn into a list of a million one-dimensional lists of 4 elements, then in theory the easiest way would be to use the Map to the Flatten function applied to the list.



But Flatten knows how to solve this problem yourself, if you indicate that levels 2 and 3 of the data structure should be merged, and level 1 is not affected. Specifying such details may be somewhat inconvenient, however using only one Flatten , our code will be executed 4 times faster than in the case when we will reinvent the capabilities built into the function.


So do not forget to look into the certificate before you enter some of its functionality.
Mathematica forgives some kinds of errors in the code, and everything will work quietly if you suddenly forgot to initialize the variable at the right moment, and you do not need to worry about recursion or unexpected data types. And it's great when you just need a quick answer. However, such a code with errors will not allow you to get the optimal solution.
Workbench helps in several ways at once. First, it allows you to better debug and organize large projects, and when everything is clear and orderly, it is much easier to write good code. But the key feature in this context is the profiler, which allows you to see which lines of code are used at certain points in time, how many times they were called.
Let us consider as an example a similar, terribly non-optimal (from the point of view of calculations) method of obtaining Fibonacci numbers . If you didn’t think about the consequences of double recursion, then you’re probably somewhat surprised by 22 seconds to estimate fib [35] (approximately the same time it will take the built-in function to calculate all 208,987,639 numbers of Fibonacci [1000000000] [see clause 3] ).

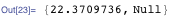
Code execution in Profiler shows the reason. The main rule is called 9 227 464 times, and the value of fib [1] is requested 18 454 929 times.
To see the code as it really is can be a real revelation.
This is a good tip for programming in any language. Here's how to do this in Mathematica :

It stores the result of calling f for any argument, so if the function is called for an argument already called earlier, then Mathematica will not need to be evaluated again. Here we give the memory, instead of receiving speed, and, of course, if the number of possible arguments to the function is huge, and the probability of re-calling a function with the same argument is very small, then you should not do so. But if the set of possible arguments is small, it can really help. This code saves the program that I used to illustrate the advice 3. It is necessary to replace the first rule with this:
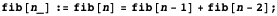
And the code starts working incomparably quickly, and to calculate fib [35] the main rule should be called only 33 times. Remembering previous results prevents the need to repeatedly recursively descend to fib [1] .
An increasing number of operations in Mathematica are automatically parallelized to local kernels (especially linear algebra, image processing, statistics), and, as we have already seen, can be implemented on demand via Compile . But for other operations that you want to parallelize on remote equipment, you can use built-in constructions for parallelization.
There is a set of tools for this, but in the case of fundamentally mono-threaded problems, using only ParallelTable , ParallelMap and ParallelTry can increase the computation time. Each of the functions automatically solves the problem of communication, control and collection of results. There are some additional costs in sending the task and getting the result, that is, getting a time gain in one, we lose time in the other. Mathematica comes with a certain maximum number of available cores (depending on license), and you can scale them with a Mathematica grid if you have access to additional cores. In this example, ParallelTable gives me double performance because it runs on my dual-core machine. A larger number of processors will give a larger increase.




Everything Mathematica can do can be parallelized. For example, you can send sets of parallel tasks to remote devices, each of which compiles and runs in C or on a GPU.
With the help of the GPU, some tasks can be solved in parallel mode much faster. Apart from the case when solving your problems, functions already optimized for CUDA are required, you need to do a little work, however, the CUDALink and OpenCLLink tools automate for you a large amount of any routine.
Due to the flexibility of data structures in Mathematica, AppendTo cannot know that you will add a number, because you can add a document, sound or image in the same way. As a result of AppendTo, you need to create a new copy of all data, restructured to accommodate the attached information. As data is accumulated, work will be slower (and the data = Append [data, value] construction is equivalent to AppendTo ).
Instead, use Sow and Reap . Sow passes the values you want to collect, and Reap collects them and creates a data object at the end. The following examples are equivalent:



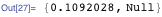
Block (localization of a variable's value), With (replacing variables in a code fragment with their specific values and then calculating the entire code) and Module (localizing variable names) are restrictive constructs that have several different properties. In my experience, Block and Module are interchangeable, at least in 95% of the cases I encounter, but Block , as a rule, works faster, and in some cases With (actually Block with read-only variables) even faster.


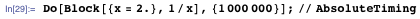
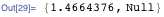
Template expressions are great. Many tasks with their help are easily solved. However, patterns are not always fast, especially such fuzzy ones as BlankNullSequence (usually recorded as "___"), which can search for patterns in the data for a long time and persistently, which obviously cannot be there. If the execution speed is fundamental, use clear models, or discard patterns altogether.
As an example, I will give an elegant way to sort a bubble into one line of code through templates:

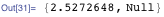
In theory, everything is neat, but too slow compared to the procedural approach that I studied when I first started programming:


Of course, in this case you should use the built-in Sort function (see tip 3), which works most quickly.


One of the strengths of Mathematica is the ability to solve problems in different ways. This allows you to write code as you think, and not to rethink the problem under the style of a programming language. However, conceptual simplicity is not always the same as computational efficiency. Sometimes an easy-to-understand idea generates more work than is necessary.
But another point is that due to all sorts of special optimizations and smart algorithms that are automatically applied in Mathematica, it is often difficult to predict which path to take. For example, here are two ways to calculate factorial, but the second is more than 10 times faster.




Why? You might assume that Do scrolls the cycles more slowly, or all these Set assignments to temp take time, or something else is wrong with the first implementation, but the real reason is likely to be quite unexpected. The Times (multiplication operator) knows a clever binary partitioning trick that can be used when you have a large number of integer arguments. Recursive separation of arguments into two smaller pieces (1 * 2 * ... * 32767) * (32768 * ... * 65536) works faster than processing all arguments, from the first to the last. The number of multiplications is the same, but however a smaller number of them include larger numbers, because on average, the algorithm is faster. There are many other hidden magic in Mathematica, and with each version of it more and more.
Of course, the best option in this case is to use the built-in function (again, tip 3):


Mathematica is able to provide superior computational performance, as well as high speed and accuracy, but not always at the same time. I hope these tips will help you balance the often conflicting demands of fast programming, fast execution, and accurate results.
All timings are given for 7 64-bit Windows PC, with 2.66 GHz Intel Core 2 Duo and 6 GB of RAM.
In addition to this brief post by John Maclone, we encourage you to read the two videos below.
Many thanks to Kirill Guzenko KirillGuzenko for help with the translation.
The post of John McLune talks about common techniques for speeding up code written in the Wolfram Language. For those interested in this issue, we recommend that you familiarize yourself with the video “Optimizing Code in Wolfram Mathematica”, from which you will learn in detail and many interesting examples about code optimization techniques, both discussed in the article (but in more detail) and others.
When people tell me that Mathematica is not fast enough, I usually ask you to look at the code and often discover that the problem is not Mathematica performance, but not optimal use. I would like to share a list of things that I pay attention to first of all when I try to optimize the code in Mathematica .
1. Use floating point numbers, and go to them as early as possible.
The most common mistake that I notice when I deal with slow code is setting too high a precision for a given task. Yes, inappropriate use of exact symbolic arithmetic is the most common case.
Most computational software systems have no such thing as exact arithmetic — for them, 1/3 is the same as 0.33333333333333. This difference can play a big role when you are faced with complex and unstable tasks, however for most tasks the floating-point numbers fully satisfy the needs, and what is important - the calculations with them are much faster. In Mathematica, any number with a dot and with less than 16 digits is automatically processed with machine precision, so you should always use a decimal point if speed is more important than precision in this task (for example, enter a third as 1./3.). Here is a simple example where working with floating-point numbers is almost 50.6 times faster than working with exact numbers, which will only be converted to floating-point numbers. And in this case the same result is obtained.
')
The same can be said for symbolic calculations. If the symbolic form of the answer is not important for you and the stability in this task does not play a special role, then try as soon as possible to proceed to the form of a floating-point number. For example, solving this polynomial equation in symbolic form, before substituting values, Mathematica builds an intermediate symbolic solution of five pages.
But if you do the substitution first, Solve will use much faster numerical methods.
When working with data lists, you should be consistent in the use of real numbers. Just one exact value in the data set will translate it into a more flexible, but less efficient form.
2. Use Compile ...
The Compile function accepts Mathematica code and allows you to pre-set the types (real, complex, etc.) and structures (value, list, matrix, etc.) of the input arguments. This deprives parts of the Mathematica language of flexibility, but frees it from having to worry about, “What if the argument is in symbolic form?” And other such things. Mathematica can optimize the program and create a bytecode to run it on its virtual machine (compilation in C is also possible - see below). Not everything can be compiled, and a very simple code may not get any advantages, however complex and low-level computational code can get really big acceleration.
Here is an example:
Using Compile instead of Function gives acceleration more than 80 times.
But we can go further by telling Compile about the possibility of parallelizing this code, getting even better results.

On my dual-core machine, I got a result 150 times faster than in the original case; The speed increase will be even more noticeable with a large number of cores.
However, it should be remembered that many functions in Mathematica , such as Table , Plot , NIntegrate, and some more automatically compile their arguments, so that you will not see any improvements when using Compile for your code.
2.5. ... and use Compile to generate code in C.
In addition, if your code is compiled, you can also use the CompilationTarget -> “C” option to generate C code, which automatically causes the C compiler to compile into a DLL and send a link to it in Mathematica . We have additional costs at the compilation stage, but the DLL is executed directly in the processor and not in the Mathematica virtual machine, so the results can be even faster (in our case, 450 times faster than the original code).

3. Use built-in functions.
Mathematica contains many features. More than an ordinary person can learn in one go (the latest version of Mathematica 10.2 already contains more than 5000 functions). So it is not surprising that I often see code where someone implements some operations, not knowing that Mathematica already knows how to implement them. And this is not only a waste of time for the invention of the bicycle; Our guys have worked hard to create and most effectively implement the best algorithms for various types of input data, so the built-in functions work really fast.
If you find something similar, but not quite, then you should check the parameters and optional arguments - they often generalize functions and cover many special and more distant applications.
Here is an example. If I have a list of a million 2x2 matrices that I want to turn into a list of a million one-dimensional lists of 4 elements, then in theory the easiest way would be to use the Map to the Flatten function applied to the list.
But Flatten knows how to solve this problem yourself, if you indicate that levels 2 and 3 of the data structure should be merged, and level 1 is not affected. Specifying such details may be somewhat inconvenient, however using only one Flatten , our code will be executed 4 times faster than in the case when we will reinvent the capabilities built into the function.
So do not forget to look into the certificate before you enter some of its functionality.
4. Use the Wolfram Workbench.
Mathematica forgives some kinds of errors in the code, and everything will work quietly if you suddenly forgot to initialize the variable at the right moment, and you do not need to worry about recursion or unexpected data types. And it's great when you just need a quick answer. However, such a code with errors will not allow you to get the optimal solution.
Workbench helps in several ways at once. First, it allows you to better debug and organize large projects, and when everything is clear and orderly, it is much easier to write good code. But the key feature in this context is the profiler, which allows you to see which lines of code are used at certain points in time, how many times they were called.
Let us consider as an example a similar, terribly non-optimal (from the point of view of calculations) method of obtaining Fibonacci numbers . If you didn’t think about the consequences of double recursion, then you’re probably somewhat surprised by 22 seconds to estimate fib [35] (approximately the same time it will take the built-in function to calculate all 208,987,639 numbers of Fibonacci [1000000000] [see clause 3] ).

Code execution in Profiler shows the reason. The main rule is called 9 227 464 times, and the value of fib [1] is requested 18 454 929 times.
To see the code as it really is can be a real revelation.
5. Remember the values that you will need in the future.
This is a good tip for programming in any language. Here's how to do this in Mathematica :
It stores the result of calling f for any argument, so if the function is called for an argument already called earlier, then Mathematica will not need to be evaluated again. Here we give the memory, instead of receiving speed, and, of course, if the number of possible arguments to the function is huge, and the probability of re-calling a function with the same argument is very small, then you should not do so. But if the set of possible arguments is small, it can really help. This code saves the program that I used to illustrate the advice 3. It is necessary to replace the first rule with this:
And the code starts working incomparably quickly, and to calculate fib [35] the main rule should be called only 33 times. Remembering previous results prevents the need to repeatedly recursively descend to fib [1] .
6. Parallelize the code.
An increasing number of operations in Mathematica are automatically parallelized to local kernels (especially linear algebra, image processing, statistics), and, as we have already seen, can be implemented on demand via Compile . But for other operations that you want to parallelize on remote equipment, you can use built-in constructions for parallelization.
There is a set of tools for this, but in the case of fundamentally mono-threaded problems, using only ParallelTable , ParallelMap and ParallelTry can increase the computation time. Each of the functions automatically solves the problem of communication, control and collection of results. There are some additional costs in sending the task and getting the result, that is, getting a time gain in one, we lose time in the other. Mathematica comes with a certain maximum number of available cores (depending on license), and you can scale them with a Mathematica grid if you have access to additional cores. In this example, ParallelTable gives me double performance because it runs on my dual-core machine. A larger number of processors will give a larger increase.
Everything Mathematica can do can be parallelized. For example, you can send sets of parallel tasks to remote devices, each of which compiles and runs in C or on a GPU.
6.5. Consider using CUDALink and OpenCLLink.
With the help of the GPU, some tasks can be solved in parallel mode much faster. Apart from the case when solving your problems, functions already optimized for CUDA are required, you need to do a little work, however, the CUDALink and OpenCLLink tools automate for you a large amount of any routine.
7. Use Sow and Reap to accumulate large amounts of data (but not AppendTo ).
Due to the flexibility of data structures in Mathematica, AppendTo cannot know that you will add a number, because you can add a document, sound or image in the same way. As a result of AppendTo, you need to create a new copy of all data, restructured to accommodate the attached information. As data is accumulated, work will be slower (and the data = Append [data, value] construction is equivalent to AppendTo ).
Instead, use Sow and Reap . Sow passes the values you want to collect, and Reap collects them and creates a data object at the end. The following examples are equivalent:
8. Use Block and With instead of Module .
Block (localization of a variable's value), With (replacing variables in a code fragment with their specific values and then calculating the entire code) and Module (localizing variable names) are restrictive constructs that have several different properties. In my experience, Block and Module are interchangeable, at least in 95% of the cases I encounter, but Block , as a rule, works faster, and in some cases With (actually Block with read-only variables) even faster.
9. Do not overdo the templates.
Template expressions are great. Many tasks with their help are easily solved. However, patterns are not always fast, especially such fuzzy ones as BlankNullSequence (usually recorded as "___"), which can search for patterns in the data for a long time and persistently, which obviously cannot be there. If the execution speed is fundamental, use clear models, or discard patterns altogether.
As an example, I will give an elegant way to sort a bubble into one line of code through templates:
In theory, everything is neat, but too slow compared to the procedural approach that I studied when I first started programming:

Of course, in this case you should use the built-in Sort function (see tip 3), which works most quickly.
10. Use different approaches.
One of the strengths of Mathematica is the ability to solve problems in different ways. This allows you to write code as you think, and not to rethink the problem under the style of a programming language. However, conceptual simplicity is not always the same as computational efficiency. Sometimes an easy-to-understand idea generates more work than is necessary.
But another point is that due to all sorts of special optimizations and smart algorithms that are automatically applied in Mathematica, it is often difficult to predict which path to take. For example, here are two ways to calculate factorial, but the second is more than 10 times faster.
Why? You might assume that Do scrolls the cycles more slowly, or all these Set assignments to temp take time, or something else is wrong with the first implementation, but the real reason is likely to be quite unexpected. The Times (multiplication operator) knows a clever binary partitioning trick that can be used when you have a large number of integer arguments. Recursive separation of arguments into two smaller pieces (1 * 2 * ... * 32767) * (32768 * ... * 65536) works faster than processing all arguments, from the first to the last. The number of multiplications is the same, but however a smaller number of them include larger numbers, because on average, the algorithm is faster. There are many other hidden magic in Mathematica, and with each version of it more and more.
Of course, the best option in this case is to use the built-in function (again, tip 3):
Mathematica is able to provide superior computational performance, as well as high speed and accuracy, but not always at the same time. I hope these tips will help you balance the often conflicting demands of fast programming, fast execution, and accurate results.
All timings are given for 7 64-bit Windows PC, with 2.66 GHz Intel Core 2 Duo and 6 GB of RAM.
In addition to this brief post by John Maclone, we encourage you to read the two videos below.
Developing large applications in Mathematica
Common mistakes and misconceptions of novice Mathematica users
Source: https://habr.com/ru/post/262879/
All Articles