Magic of tensor algebra: Part 9 - Derivation of the angular velocity tensor through the parameters of the final rotation. Apply Maxima

Content

Introduction

The order of time has already flowed away, as I promised to get the tensor of the angular velocity of a solid body, expressing it through the parameters of the final rotation. If you look at the KDPV, it will become clear why I thought so long - a stack of paper on the table, this is the course of my thoughts.

The transformation of tensor expressions is still a pleasure ...

')
Cruel tensors did not want to be simplified. Rather, they wanted it, but during transformations, disclosure of parentheses, due to carelessness, minor errors occurred that did not allow to look at the whole picture. As a result, the result was still obtained. SKA Maxima, which I addressed, played a significant role in this, thanks in large part to an article by EugeneKalentev . The emphasis of the mentioned article shifted towards computational work with tensors, the components of which are represented by concrete data structures. I was also interested in the question of working with abstract tensors. It turned out that Maxima can work with them, although not as much as she could be, but still she has seriously simplified my life.

So, we return to solid mechanics, and at the same time we will look at how to work with tensors in Maxima.

1. A little about the final expression of the rotation tensor

In the last article, we, having studied the principles of convolution of the product of Levi-Civita tensors, obtained this expression for the rotation tensor

$B_k ^ {\, m} = u ^ {\, m} \, g_ {jk} \, u ^ {\, j} - \ cos \ varphi \, \ left (\ delta_ {j} ^ {\, m } \, \ delta_ {k} ^ {\, q} - \ delta_ {k} ^ {\, m} \, \ delta_ {j} ^ {\, q} \ right) \, u_ {q} \, u ^ j + \ sin \ varphi \, g ^ {mi} \, U_ {ik} \ right \ quad (1)$

It can be simplified, for this we will work with the expression in brackets in the second term

$\ left (\ delta_ {j} ^ {\, m} \, \ delta_ {k} ^ {\, q} - \ delta_ {k} ^ {\, m} \, \ delta_ {j} ^ {\, q} \ right) \, u_ {q} \, u ^ j = \ delta_ {j} ^ {\, m} \, \ delta_ {k} ^ {\, q} \, u_ {q} \, u ^ j - \ delta_ {k} ^ {\, m} \, \ delta_ {j} ^ {\, q} \, u_ {q} \, u ^ j =$

$= u ^ m \, u_ {k} - \ delta_ {k} ^ {\, m} \, u ^ q \, u_ {q} = u ^ m \, u_ {k} - \ delta_ {k} ^ {\, m} \ quad (2)$

And all because convolution of the tensor with the Kronecker delta leads to the replacement of the silent tensor index by the free Kronecker delta index, for example $\ delta_ {k} ^ {\, q} \, u_ {q} = u_ {k}$ . Acting in this way, and taking into account that the vector $\ vec {u}$ has a length equal to one, which means convolution $u ^ {q} \, u_ {q} = 1$ we get (2). Then the rotation tensor expression looks even simpler.

$B_k ^ {\, m} = \ left (1 - \ cos \ varphi \ right) u ^ {\, m} \, u _ {\, k} + \ cos \ varphi \, \ delta_ {k} ^ {\ , m} + \ sin \ varphi \, g ^ {mi} \, U_ {ik} \ right \ quad (3)$

just the expression that I have long and tediously tried to derive in the seventh article . Which again confirms the rule that nothing can be studied in half ...

For what I did it all. First, finally rehabilitated in the eyes of readers. Secondly - so that we have something to compare the results that we get below with the help of Maxima. And thirdly, to say that on expression (3) our sweet life ends and the hell of monstrous transformations begins.

2. We use Maxima to derive the angular velocity tensor

The itensor module, the documentation for which is presented in the original , translated into Russian , and another book based on documentation, is responsible for working with abstract tensors in Maxima.

We start Maxima, even in the console, even using one of its graphic frontends, and we write

 kill(all); load(itensor); imetric(g); idim(3);

Here we clean the memory (the kill() function), removing all definitions and loaded modules from it, load the itensor package (the load() function), say that the metric tensor will be called g (the imetric() function), and also we indicate the dimension of the space ( idim() function), because by default, the SKA considers that it works in 4-dimensional space-time with the Riemann metric. We are working in the three-dimensional space of classical mechanics, and our metric is any non-degenerate torsion-free.

Enter the rotation tensor

 B:ishow( u([],[l])*g([j,k],[])*u([],[j]) - cos(phi)*'levi_civita([],[l,q,i])*u([q],[])*'levi_civita([i,j,k],[])*u([],[j]) + sin(phi)*g([],[l,i])*'levi_civita([i,j,k])*u([],[j]))$

In itensor tensors are declared by an identifier, after which the lists of covariant and contravariant indices are indicated in brackets, separated by commas. The levi_civita() function sets the Levi-Civita tensor, and the prime in front of it means that this tensor does not need to be calculated. Maxima is known for her way of calculating and simplifying expressions if it is possible, and if the stroke is not set, then the Levi-Civita tensor will turn into a “pumpkin”, and specifically, an attempt will be made to define it through the generalized Kronecker delta, which is not our plan.

The $ symbol is an alternative to the semicolon and prohibits the display of conversion results. We will use ishow() to display the information. The expression inserted into it is displayed on the screen in the usual index notation for recording tensors. On the screen it looks like this

Moreover, we introduce its non-simplified form, with a double vector product, without introducing an antisymmetric tensor $\ mathbf {U}$ so that at the first stage we obtain (3) and check how the machine simplifies tensor expressions. In human form, this expression looks like this.

$g_ {j \, k} \, u ^ {l + j} - \ varepsilon_ {i \, j \, k} \, \ cos \ Phi \, \ varepsilon ^ {i \, l \, q} \, u_ {q} \, u ^ {j} + g ^ {i \, l} \, \ varepsilon_ {i \, j \, k} \, \ sin \ Phi \, u ^ {j}$

although the sum of the indices in the first term leads to suspicions of some special magic that is unknown to us. But this output is generated directly by Maxima, using the spell

 load(tentex); tentex(B);

which allows you to get the output in the form of code LaTeX. Among the shortcomings - shamanism with indices and a capital letter indicating the angle of rotation, but both are correctable in principle, and Maxima pleased me with the fact that it generates a TeX output that is not as redundant as, for example, Maple.

Go ahead. Next we recall the expression that determines the angular velocity through the tensor of rotation

$\ Omega _ {\, mk} = g _ {\, mp} \, B_ {l} ^ {'\, p} \, \ dot {B} _ {k} ^ {\, l} \ quad (4)$

Now imagine that we have to differentiate (3) by time, then multiply the derivative by the inverse matrix (3) and the metric tensor. This can be done manually, but if I had brought this process to the end, the stack of sheets on the table would be three times thicker.

First, simplify the introduced rotation tensor.

 B:ishow(expand(lc2kdt(B)))$

The function lc2kdt() designed specifically to simplify expressions containing the Levi-Civita tensor. She tries to minimize this tensor where it is possible, giving a combination of sums and works of Kronecker's deltas. So the result looks like

The expand() function is also applied to the lc2kdt() result, which expands the parentheses. Without this, Maxima performs the convolution very reluctantly.

Now we will try to calculate the resulting expression by performing a convolution. The contract() function is one of the most reliable ways to perform convolution.

 B01:ishow(contract(B))$

At the output we get (where possible, I will bring LaTeX output generated by Maxima using the tentex() function)

$\ delta_ {k} ^ {l} \, \ cos \ Phi \, u_ {q} \, u ^ {q} -u_ {k} \, \ cos \ Phi \, u ^ {l} + u_ {k } \, u ^ {l} + g ^ {i \, l} \, \ varepsilon_ {i \, j \, k} \, \ sin \ Phi \, u ^ {j}$

which is similar to expression (3). This convinced me of the correctness of the program and the correctness of their own actions. So you can move on.

The only thing that does not take into account Maxima is that the vector around which the rotation is made has a length equal to one. Therefore, it does not minimize the expression $u ^ {q} \, u_ {q}$ in the scalar. I didn’t think up how to tell him about it and didn’t read it in the documentation, although I searched it carefully. In the future, this will give serious difficulties, which we will discuss, but for the time being I got out with the help of a crutch, replacing the uncomfortable tensors with a unit

 B01:ishow(subst(1, u([],[q]), B01))$ B01:ishow(subst(1, u([q],[]), B01))$

The expression of the rotation tensor through the parameters of the final rotation has the pleasant property that obtaining an inverse matrix is reduced to the substitution in (3) of the angle of rotation with the opposite sign. Indeed, turning in the other direction is the inverse transformation. This can be proved strictly mathematically, based on the properties of the rotation matrix. I have done this and consider it redundant in this article. Just get the inverse transform tensor

 B10:ishow(subst(-phi, phi, B01))$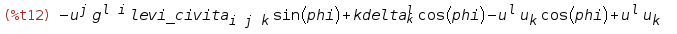

Since we are going to take the derivative, Maxima needs to know which tensors and numerical parameters depend on time. We indicate that the direction of the axis of rotation and the angle of rotation depend on time

 depends([u,phi], t);

To make our tensors correspond to formula (4), we will rename the indices

 B10:ishow(subst(p,l,B10))$ B10:ishow(subst(l,k,B10))$ B10:ishow(subst(i1,i,B10))$ B10:ishow(subst(j1,j,B10))$ B10:ishow(subst(s,q,B10))$

Thus, we changed the names of free indices, for correct multiplication in (4), and redefined the names of dumb indices. According to the rules, it is assumed that the names of dumb indices in the multiplied tensors do not coincide.

Now we take the time derivative of the rotation tensor

 dBdt:ishow(diff(B01,t))$

getting out

We are convinced that the differentiation was performed correctly. Finally, we introduce formula (4), applying successively opening the brackets and simplification, taking into account the Levi-Civita tensor

 exp1:ishow(lc2kdt(expand(g([m,p],[])*B10*dBdt)))$

What is the result, scary to show, but if you please

Understand anything in this mess is difficult. But it is clear that the Kronecker delta combinations (the kdelta() function sets the Kronecker delta of any desired rank) with a strange designation of mute indices containing the number after % . The fact is that Maxima, when converting, numbers the dumb indices. Let's try to simplify it all.

First, once again, we use the expression through simplification, taking into account the Levi-Civita tensor ( lc2kdt() ). Then we perform the convolution ( contract() ). After that, we will try to simplify our “crocodile” by applying the canform() function to it, which performs the numbering of the silent indices and the simplification of the tensor. This feature is recommended by developers to perform simplifications.

 exp2:ishow(canform(contract(lc2kdt(exp1))))$

As a result, we observe a serious slimming "crocodile"

But! In the first term, we see the vector product of the orth axis of the axis of rotation on itself, and it must be equal to zero. Maxima has not yet understood this, she must point out the possibility of such a simplification. We make it a construction

 exp3:ishow(canform(contract(expand(applyb1(exp2,lc_l,lc_u)))))$

The applyb1() function sets the rules for simplifying the subexpressions included in the simplified expression. An expression and a list of rules are passed as arguments. We have two rules: lc_l and lc_u are rules for converting subexpressions with the Levi-Civita symbol with lower ( lc_l ) and upper ( lc_u ) indices. At the same time, we again open parentheses that may appear after transforming subexpressions, perform convolution and simplification. As a result, we observe another reduction in the crocodile mass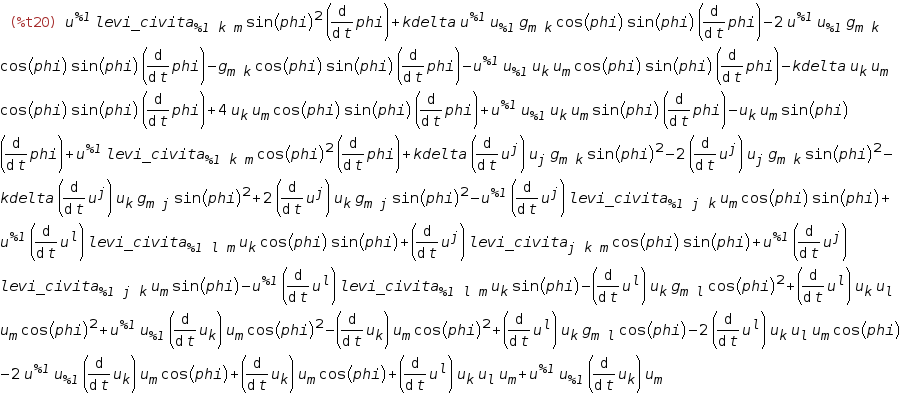

Perhaps this is not the limit. But I was surprised, probably due to ignorance and lack of experience following

Pay attention to the variable kdelta . Experiments with Maxima made it possible to find out that this is a trace of the Kronecker delta of 2 ranks, equal to the dimension of space (the trace of the identity matrix). In our case, this number is "3". The three must stand in place of kdelta . But for some reason it is not worth it; perhaps the configuration variables of the tensor package are somehow incorrectly configured. If we take kdelta equal to three, then a bunch of various sign like terms is formed, which together give zero.
All convolutions of the form
$u ^ {i} \, u_ {i}$

This is the module of the orth of rotation, but it does not change and is equal to one. How to say about this Maxima for me has not yet been clarified.
It follows from the previous problem, for
$u ^ i \, u_i = 1$

which means

$\ dot u ^ {i} \, u_ {i} + u ^ {i} \, \ dot u_ {i} = 0 & quot;$

where, by virtue of the commutativity of the operation of scalar multiplication, we have

$\ dot u ^ {i} \, u_ {i} = 0, \ quad u ^ {i} \, \ dot u_ {i} = 0 & quot;$

The last expressions are often found in the above result.

I would be extremely grateful for the hint of those who know about the above problems, because studying the documentation has not yet shed light on the solution. The replacement function subst() does not work here.

In this regard, I again took up pen and paper in order to “supplement” the angular velocity tensor. But Maxima has greatly facilitated my task, for which she thanks.

3. With a pen, paper, file and tambourine ...

We write out all nonzero terms, we give similar ones, we put the common factors out of the brackets. Surprisingly, everything beautifully and quickly collapses into the formula

$\ Omega _ {\, km} = \ left (1 - \ cos \ varphi \ right) \ left (\ dot u _ {\, k} \, u _ {\, m} - u _ {\, k} \, \ dot u _ {\, m} \ right) + \ sin \ varphi \, \ left (1 - \ cos \ varphi \ right) \, u ^ {\, i} \ left (\ varepsilon _ {\, ijk} \, \ dot u ^ {\, j} \, u _ {\, m} - \ varepsilon _ {\, ilm} \, \ dot u ^ {\, l} \, u _ {\, k} \ right) +$

$+ \ sin \ varphi \ cos \ varphi \, \ dot u ^ {\, j} \ varepsilon _ {\, jkm} + \ dot \ varphi \, \ varepsilon _ {\, ikm} \, u ^ {i} \ quad (five)$

This expression painfully resembles, a similar one, obtained for an orthogonal basis and expressed in a matrix form.

Pogorelov D. Yu. Introduction to modeling the dynamics of systems of bodies. Page 31.

The tensor (5) is antisymmetric, we rearrange the indices, changing the signs of the corresponding expressions. The first term is the difference of covariant tensor products, the second is the first transposed, and this sum gives an antisymmetric tensor at the output. The remaining terms contain the Levi-Civita tensor, which changes sign when the indices are interchanged.

$\ Omega _ {\, mk} = \ left (1 - \ cos \ varphi \ right) \ left (\ dot u _ {\, m} \, u _ {\, k} - u _ {\, m} \, \ dot u _ {\, k} \ right) + \ sin \ varphi \, \ left (1 - \ cos \ varphi \ right) \, u ^ {\, i} \ left (\ varepsilon _ {\, ilk} \, \ dot u ^ {\, l} \, u _ {\, m} - \ varepsilon _ {\, ijm} \, \ dot u ^ {\, j} \, u _ {\, k} \ right) +$

$- \ sin \ varphi \ cos \ varphi \, \ dot u ^ {\, j} \ varepsilon _ {\, jmk} - \ dot \ varphi \, \ varepsilon _ {\, imk} \, u ^ {i}$

And once again, rearrange the indices in the last two terms.

$+ \ sin \ varphi \ cos \ varphi \, \ varepsilon _ {\, mjk} \, \ dot u ^ {\, j} + \ dot \ varphi \, \ varepsilon _ {\, mik} \, u ^ {i} \ quad (6)$

so that their convolution gives skew-symmetric matrices, which are customary for the representation of the vector product in the matrix form.

A further simplification (6) is possible if we take the base as Cartesian. Then the covariant and contravariant components coincide, the nonzero elements of the Levi-Chevita tensor modulo become equal to one, and (6) can be simplified a little more. We got this expression for an arbitrary basis.

Conclusion

So, thanks to Maxima tensor tools, I finally figured out the task of expressing the angular velocity tensor through the parameters of the final rotation. And at the same time showed the reader a living example of working with tensors in the SKA.

Next time, we will obtain from (6) the pseudovectors of angular velocity and angular acceleration and closely approach the tensor description of the kinematics of a solid body.

Thank you for attention!

To be continued…

Source: https://habr.com/ru/post/262801/

All Articles