Multiplication of Karatsuba and C ++ 11
I want to once again touch on the method of implementing Karatsuba multiplication using the capabilities of the C ++ standard 11. This algorithm was repeatedly considered here ( “Multiplication of long numbers using the Karatsuba method” , “Karatsuba algorithm for multiplying two numbers” ), but apparently due to the fact that I cannot prepare them, the first version did not work with numbers of different lengths, and the second does not exactly what was needed.
For those who are not tired of this hackneyed topic, as well as all those who have difficulties with the implementation of this simple but very effective algorithm, please read further.

All of us were taught to multiply in a column at school. This is the simplest algorithm that has been known for thousands of years:
')
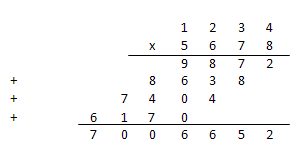
Even Andrei Nikolaevich Kolmogorov in 1956 formulated a hypothesis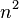 (which was the lower estimate of the multiplication of the order of
(which was the lower estimate of the multiplication of the order of 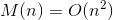 ), since if there were any other faster algorithm, then in such a huge period of time it would have been found.
), since if there were any other faster algorithm, then in such a huge period of time it would have been found.
The pseudocode of naive multiplication is as simple as the method itself:
For simplicity, sometimes you have to pay performance, but you can optimize this algorithm and not calculate the remainder at each step.
A few years after the formulation of the Kolmogorov hypothesis, Anatoly Alekseevich Karatsuba found a faster method. His approach was generalized to the divide-and-conquer paradigm. To understand how this works, consider two numbers of length.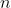 which we break into two lengths
which we break into two lengths  :
:
![\\ X = \ left [X_l \ right] \ left [X_r \ right] = 10 ^ {\ frac {n} {2}} \ cdot X_l + X_r \\ Y = \ left [Y_l \ right] \ left [ Y_r \ right] = 10 ^ {\ frac {n} {2}} \ cdot Y_l + Y_r](https://latex.codecogs.com/gif.latex?\\X&space;=&space;\left&space;[&space;X_l&space;\right&space;]\left&space;[&space;X_r&space;\right&space;]=10^{\frac{n}{2}}\cdot&space;X_l&space;+&space;X_r&space;\\Y&space;=&space;\left&space;[&space;Y_l&space;\right&space;]\left&space;[&space;Y_r&space;\right&space;]=10^{\frac{n}{2}}\cdot&space;Y_l&space;+&space;Y_r)
Now note that [1]:
\cdot\left(10^{\frac{n}{2}}\cdot&space;Y_l+Y_r\right)=\newline=10^n&space;X_l\cdot&space;Y_l+10^{\frac{n}{2}}\left(X_l\cdot&space;Y_r+X_r\cdot&space;Y_l\right)+X_r\cdot&space;Y_r)
It is seen that it is necessary to make 4 multiplications and then the complexity is no different from the naive algorithm. But Anatoly Alekseevich Karatsuba noticed that you can get by with 3 multiplications of numbers of length -
-  ,
,  ,
, \cdot&space;\left(&space;Y_l&space;+&space;Y_r&space;\right&space;)) . Really:
. Really:
\cdot\left(Y_l&space;+&space;Y_r&space;\right&space;)&space;-&space;X_l\cdot&space;Y_l&space;-&space;X_r\cdot&space;Y_r)
We managed three multiplications instead of four, and therefore the operation time of the Karatsuba algorithm satisfies the relation [2]:
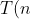=3T\left(\frac{n}{2}\right)+O(n)) ,
,
which ultimately gives the overall complexity of the algorithm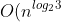) .
.
Karatsuba multiplication code pseudodode:
And an example on small numbers to fix the mechanism of work:
So we are ready to start implementing the algorithm in C ++. On the Internet, I found several implementations that use the C-style of writing code, which makes it somewhat difficult to read for beginners. Therefore, I decided to use as much as possible the improvements available in the C ++ 11 standard. Yes, it will slow down the code, but here we are primarily interested in ease of understanding and readability.
To build the test program, Clang ++ with the -O3 key was used. The test results for the representation of numbers with a base of 10 are shown in Figure 1.
It can be seen that the naive algorithm significantly slows down when input numbers are longer .
.
Figure 2 shows the result of the work of the same algorithms, but with a small optimization. Now the long number is placed in the vector using base 100, which gives a significant increase in performance.
That's all, we have disassembled with you this simple and effective way of multiplying. I hope this material will be useful and many newbies who are just starting to learn the algorithms will no longer fall into a stupor (well, he did not come to me the first time in his time).
There is still much to optimize this implementation:
That's all, thank you all for your attention.
The original project that was used when writing the article is here .
For those who are not tired of this hackneyed topic, as well as all those who have difficulties with the implementation of this simple but very effective algorithm, please read further.
Table of contents
- Introduction
- Implementation
- Comparison of the speed of the naive algorithm and the Karatsuba algorithm
- findings
Introduction

All of us were taught to multiply in a column at school. This is the simplest algorithm that has been known for thousands of years:
')
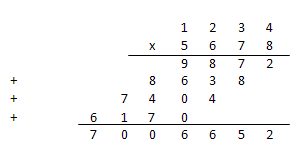
Even Andrei Nikolaevich Kolmogorov in 1956 formulated a hypothesis
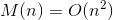 ), since if there were any other faster algorithm, then in such a huge period of time it would have been found.
), since if there were any other faster algorithm, then in such a huge period of time it would have been found.The pseudocode of naive multiplication is as simple as the method itself:
multiply(x[0 ... l], y[0 ... r]): res = [0 ... r+l] for (i = 0, i < r; ++i): carry = 0 for (j = 0, j < l; ++j): res[i + j] += carry + x[i] * y[j] carry = res[i + j] / base // base - res[i + j] %= base res[i + l] += carry For simplicity, sometimes you have to pay performance, but you can optimize this algorithm and not calculate the remainder at each step.
A few years after the formulation of the Kolmogorov hypothesis, Anatoly Alekseevich Karatsuba found a faster method. His approach was generalized to the divide-and-conquer paradigm. To understand how this works, consider two numbers of length.
Now note that [1]:
It is seen that it is necessary to make 4 multiplications and then the complexity is no different from the naive algorithm. But Anatoly Alekseevich Karatsuba noticed that you can get by with 3 multiplications of numbers of length
We managed three multiplications instead of four, and therefore the operation time of the Karatsuba algorithm satisfies the relation [2]:
which ultimately gives the overall complexity of the algorithm
Karatsuba multiplication code pseudodode:
Karatsuba_mul(X, Y): // X, Y - n n = max( X, Y) n = 1: X * Y X_l = n/2 X X_r = n/2 X Y_l = n/2 Y Y_r = n/2 Y Prod1 = Karatsuba_mul(X_l, Y_l) Prod2 = Karatsuba_mul(X_r, Y_r) Prod3 = Karatsuba_mul(X_l + X_r, Y_l + Y_r) Prod1 * 10 ^ n + (Prod3 - Prod1 - Prod2) * 10 ^ (n / 2) + Prod2 And an example on small numbers to fix the mechanism of work:
a = 12 b = 81 res = Karatsuba_mul(a, b): // a = b = 2 n = max( a, b) // n = 2 X_l = 1, X_r = 2 // 1 | 2 Y_l = 8, Y_r = 1 // 8 | 1 Prod1 = Karatsuba_mul(1, 8) // Prod1 = 8 Prod2 = Karatsuba_mul(2, 1) // Prod2 = 2 Prod3 = Karatsuba_mul(3, 9) // Prod3 = 27 8 * 10 ^ 2 + (27 - 2 - 8) * 10 + 2 ----------------------------------------------- res = 972 Implementation
So we are ready to start implementing the algorithm in C ++. On the Internet, I found several implementations that use the C-style of writing code, which makes it somewhat difficult to read for beginners. Therefore, I decided to use as much as possible the improvements available in the C ++ 11 standard. Yes, it will slow down the code, but here we are primarily interested in ease of understanding and readability.
- Storage number. We use the standard vector of integers with which everyone studying C ++ is familiar. We will read a long number in a line and from the end be divided into digits corresponding to the selected base (10 at the beginning).
For example, the input received a number:123456789000000000
In our container it will be stored as:|0|1|2|3|4|5|...|n| 0 0 0 0 0 0 ... 1Function code get_number ()vector<int> get_number(istream& is) { string snum; vector<int> vnum; // unsigned int dig = 1; int n = 0; is >> snum; for (auto it = snum.crbegin(); it != snum.crend(); ++it) { n += (*it - '0') * dig; dig *= dig_size; // , if (dig == base) { vnum.push_back(n); n = 0; dig = 1; } } if (n != 0) { vnum.push_back(n); } return vnum; } - Getting the number. At the entrance, we can receive numbers of different lengths and for the successful operation of the algorithm, it is desirable for us to reduce to the same length, a multiple of 2 (since we constantly divide our “long” numbers in half). Let's write the extend_vec () function that would take our vector and extend it somehow like this:
first = {4}; // 4; size = 1 second = {3, 2, 1} // 123; size = 3 auto n = max(first.size(), second.size()); extend_vec(first, n); // 3 extend_vec(second, n); // 1Extend_vec () function codevoid extend_vec(vector<int>& v, size_t len) { while (len & (len - 1)) { ++len; } v.resize(len); } - Multiplication. Here it is worth talking about several optimizations that are worth doing. We will not count the residuals and transfer them to the higher digits on each recursive call, but at the end. And for multiplying two numbers with a length less than, say, 128, we will use a naive algorithm, since it is a smaller constant than the Karatsuba algorithm.Function code naive_mul ()
vector<int> naive_mul(const vector<int>& x, const vector<int>& y) { auto len = x.size(); vector<int> res(2 * len); for (auto i = 0; i < len; ++i) { for (auto j = 0; j < len; ++j) { res[i + j] += x[i] * y[j]; } } return res; }Karatsuba_mul () function codevector<int> karatsuba_mul(const vector<int>& x, const vector<int>& y) { auto len = x.size(); vector<int> res(2 * len); if (len <= len_f_naive) { return naive_mul(x, y); } auto k = len / 2; vector<int> Xr {x.begin(), x.begin() + k}; vector<int> Xl {x.begin() + k, x.end()}; vector<int> Yr {y.begin(), y.begin() + k}; vector<int> Yl {y.begin() + k, y.end()}; vector<int> P1 = karatsuba_mul(Xl, Yl); vector<int> P2 = karatsuba_mul(Xr, Yr); vector<int> Xlr(k); vector<int> Ylr(k); for (int i = 0; i < k; ++i) { Xlr[i] = Xl[i] + Xr[i]; Ylr[i] = Yl[i] + Yr[i]; } vector<int> P3 = karatsuba_mul(Xlr, Ylr); for (auto i = 0; i < len; ++i) { P3[i] -= P2[i] + P1[i]; } for (auto i = 0; i < len; ++i) { res[i] = P2[i]; } for (auto i = len; i < 2 * len; ++i) { res[i] = P1[i - len]; } for (auto i = k; i < len + k; ++i) { res[i] += P3[i - k]; } return res; } - Normalization. It remains to make all transfers and you can display the result (or use for further calculations).Function code finalize ()
void finalize(vector<int>& res) { for (auto i = 0; i < res.size(); ++i) { res[i + 1] += res[i] / base; res[i] %= base; } }
And display the result, complementing with zeros when using a base greater than 10.Function code print_res ()void print_res(const vector<int>& v, ostream& os) { auto it = v.crbegin(); // Passing leading zeroes while (!*it) { ++it; } while (it != v.crend()) { int z = -1; int num = *it; if (num == 0) { num += 1; } if (num < add_zero) { z = 1; while ((num *= dig_size) < add_zero) { ++z; } } if (z > 0) { while (z--) { os << '0'; } } os << *it++; } os << endl; }
Comparison of the speed of the naive algorithm and the Karatsuba algorithm
To build the test program, Clang ++ with the -O3 key was used. The test results for the representation of numbers with a base of 10 are shown in Figure 1.
Calculation time of the work (base 10)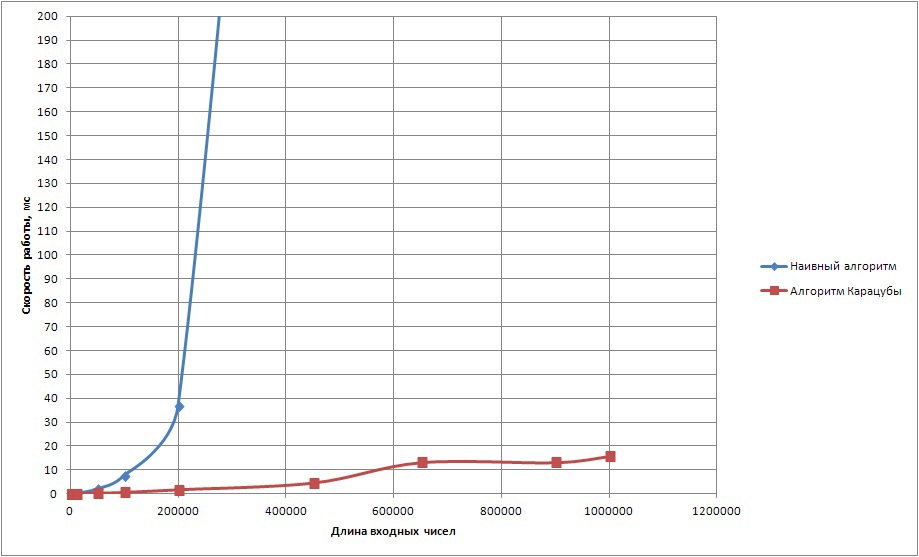
Figure 1. Calculation time for the product of two numbers using the base 10 representation

Figure 1. Calculation time for the product of two numbers using the base 10 representation
It can be seen that the naive algorithm significantly slows down when input numbers are longer
Figure 2 shows the result of the work of the same algorithms, but with a small optimization. Now the long number is placed in the vector using base 100, which gives a significant increase in performance.
Calculation time of the work (base 100)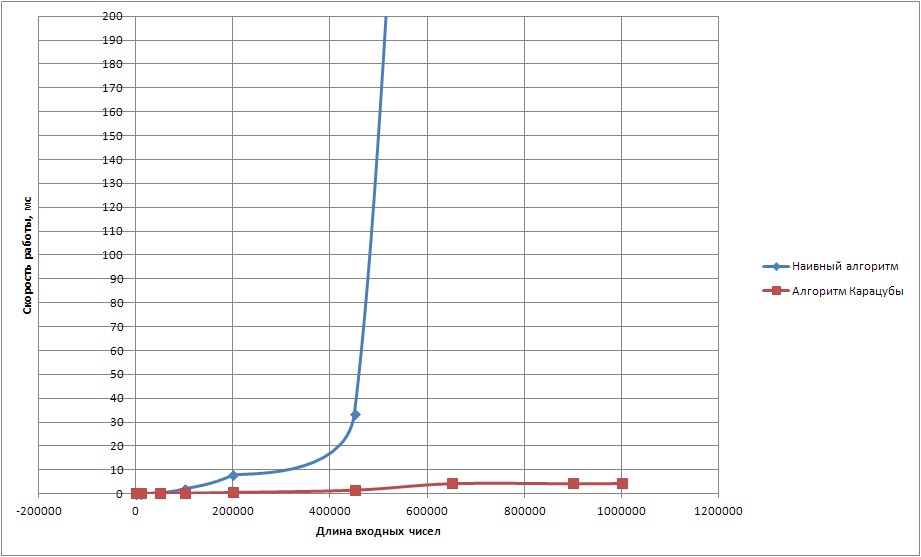
Figure 2. Calculation time for the product of two numbers, using the base 100 representation

Figure 2. Calculation time for the product of two numbers, using the base 100 representation
findings
That's all, we have disassembled with you this simple and effective way of multiplying. I hope this material will be useful and many newbies who are just starting to learn the algorithms will no longer fall into a stupor (well, he did not come to me the first time in his time).
There is still much to optimize this implementation:
- increase the base in which the numbers are stored in the vector. Now the normalization of the number is done at the very end, which causes an overflow of standard types in C ++. It may be worth storing numbers in an array / vector of unsigned long long type and calculate the residuals with hyphenation at each stage of multiplication. Or use the "long" representation of the remainder.
- abandon vectors in favor of arrays and not use the selection of the left and right side of the number using iterators.
That's all, thank you all for your attention.
The original project that was used when writing the article is here .
Bibliography
- S. Dasgupta Algorithms: Translated from English by A. S. Kulikov, edited by A. Shen [Text] / S. Dasgupta, H. Papadimitriou, U. Vazirani. -Moscow: ICNMO, 2014 - 320 p.
- Karatsuba algorithm [Electronic resource] / Wikipedia - URL: en.wikipedia.org/wiki/Karatsuba_algorithm
- A. S. Kulikov Algorithms and data structures [Electronic resource] / A. S. Kulikov - URL: https://stepic.org/course/Algorithms- and structures- data-63/ syllabus
Source: https://habr.com/ru/post/262705/
All Articles