How to solve the entrance exam to the Yandex Data Analysis School
Summer is the time for entrance exams. The selection to the Yandex Data Analysis School is being completed right now - interviews are being held for those who have already passed the exam. In SAD teaching machine learning, computer vision, analysis of texts in natural language and other areas of modern Computer Science. For two years, students study subjects that are usually not included in university programs, although they are in great demand both in science and in industry. One can study not only in Moscow - branches have been opened in the School in Yekaterinburg, Minsk, Kiev, Novosibirsk, St. Petersburg. There is also a correspondence department, where you can study by watching video lectures and correspondence with the teachers of the Moscow School by mail.
But in order to enter the ShAD, you need to successfully complete three stages - fill out a form on the site , pass the entrance exam and come in for an interview. Every year, undergraduates, graduates and postgraduates of MSU, MIPT, HSE, ITMO, SPbSU, UrFU, NSU enter the ShAD and not all of them cope with our tests. This year we received questionnaires from 3,500 people, 1,000 of whom were admitted to the exam, and only 350 passed it successfully.
')
For those who want to try themselves and understand what he is capable of, we have prepared a review of this year’s entrance exam. With the option that we have chosen for you, 56% managed it. In this table you can see how many people were able to solve each of the tasks in it.
But for a start, I would like to explain that we are testing with an exam and how we approach it. In the very first years of the ShAD, there was no written exam, as there were few more applications, and it turned out to talk with all those who had passed the online testing. But then the interviews were longer; Some graduates recall having six hours of conversation with them, offering many difficult tasks. Then there were more applicants - and in 2012 there was a written exam.
The creation of the variant is done by the curators of the Moscow ShAD, one of which I am; with the selection of tasks they are helped by colleagues from the branches. The number of tasks in the variant has not changed much in these four years: first there were seven, and last year it was eight. In each variant there are tasks in mathematics (from five to seven) and tasks for algorithms (one or two).
As for mathematics, we, of course, check whether the applicants possess the main sections of the program: algebra, mathematical analysis, combinatorics, and probability theory. But it’s important for us not to know what is achieved by bog and forgotten a week after the test or exam - like horrible formulas from the table of indefinite integrals or the Student’s distribution function; this is why we allow applicants to take any paper sources with us for the written exam. Understanding the essence of what is happening, as well as the ability to apply standard facts and methods in unusual situations, is much more valuable. We also try to minimize computational complexity; even two-digit numbers must be multiplied infrequently. So, in the exam you will not find routine and tedious computational exercises, and many tasks will seem non-standard and maybe even Olympiad.
In terms of algorithms, we avoid tasks that require knowledge of specific data structures (search trees, hash tables, etc.) or algorithms (fast sorting algorithms, shortest path algorithms on graphs, etc.). In addition, we do not require applicants to write an implementation of the invented algorithm in any programming language; rather, on the contrary, in every way we dissuade it. Indeed, in the written exam, we are most interested not in programming skills, but in the ability to clearly describe the algorithm and, if necessary, convince the reader that it satisfies the limitations on the running time and the amount of allocated memory. However, decisions that contain code in any language that we are able to read are also made, but they are more difficult to verify and, moreover, they must still be accompanied by a justification for correctness.
Find the limit of the sequence (a n ) for which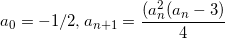
On a plane tiled with the same rectangles with sides 10 and 20 (the rectangles are adjacent to the sides), draw a random circle of radius 4. Find the probability that the circle has common points with exactly three rectangles.
Dima and Vanya take turns filling in a 2n × 2n matrix. Vanya's goal is to make the resulting matrix have an eigenvalue of 1, and Dima's goal is to prevent him. Dima goes first. Do any of them have a winning strategy?
Find the determinant of the matrix A = (a ij ) , where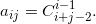
Given two arrays of integers a [1..n] and b [1..k] , all elements of b are different. It is required to find a set of indices i_1 <i_2 <... <i_k , for which the set a [i_1], ..., a [i_k] is a permutation of the elements of the array b, and the difference i_k - i_1 is the minimum possible. The time limit is O (nk) (but maybe you can be faster), by memory O (n) .
In 2222, volleyball tournaments are held under the new system. They say that team A exceeds team B if A won against B or any team that won against B. Each pair of teams plays 1 time each. A draw is excluded by volleyball rules. The champion is announced a team that surpasses all other teams. (a) Prove that there will be a champion (b) Prove that there cannot be exactly two champions.
Calculate the integral
On the plane there is a broken line with n links. The length of each link is 1, the oriented angle between adjacent links with equal probability is α or –α . Find the expected value of the square of the distance from its starting point to the end.
But in order to enter the ShAD, you need to successfully complete three stages - fill out a form on the site , pass the entrance exam and come in for an interview. Every year, undergraduates, graduates and postgraduates of MSU, MIPT, HSE, ITMO, SPbSU, UrFU, NSU enter the ShAD and not all of them cope with our tests. This year we received questionnaires from 3,500 people, 1,000 of whom were admitted to the exam, and only 350 passed it successfully.
')
For those who want to try themselves and understand what he is capable of, we have prepared a review of this year’s entrance exam. With the option that we have chosen for you, 56% managed it. In this table you can see how many people were able to solve each of the tasks in it.
| The task | one | 2 | 3 | four | five | 6 | 7 | eight |
| Decided | 57% | 68% | 40% | 35% | 29% | 12% | 20% | 6% |
But for a start, I would like to explain that we are testing with an exam and how we approach it. In the very first years of the ShAD, there was no written exam, as there were few more applications, and it turned out to talk with all those who had passed the online testing. But then the interviews were longer; Some graduates recall having six hours of conversation with them, offering many difficult tasks. Then there were more applicants - and in 2012 there was a written exam.
The creation of the variant is done by the curators of the Moscow ShAD, one of which I am; with the selection of tasks they are helped by colleagues from the branches. The number of tasks in the variant has not changed much in these four years: first there were seven, and last year it was eight. In each variant there are tasks in mathematics (from five to seven) and tasks for algorithms (one or two).
As for mathematics, we, of course, check whether the applicants possess the main sections of the program: algebra, mathematical analysis, combinatorics, and probability theory. But it’s important for us not to know what is achieved by bog and forgotten a week after the test or exam - like horrible formulas from the table of indefinite integrals or the Student’s distribution function; this is why we allow applicants to take any paper sources with us for the written exam. Understanding the essence of what is happening, as well as the ability to apply standard facts and methods in unusual situations, is much more valuable. We also try to minimize computational complexity; even two-digit numbers must be multiplied infrequently. So, in the exam you will not find routine and tedious computational exercises, and many tasks will seem non-standard and maybe even Olympiad.
In terms of algorithms, we avoid tasks that require knowledge of specific data structures (search trees, hash tables, etc.) or algorithms (fast sorting algorithms, shortest path algorithms on graphs, etc.). In addition, we do not require applicants to write an implementation of the invented algorithm in any programming language; rather, on the contrary, in every way we dissuade it. Indeed, in the written exam, we are most interested not in programming skills, but in the ability to clearly describe the algorithm and, if necessary, convince the reader that it satisfies the limitations on the running time and the amount of allocated memory. However, decisions that contain code in any language that we are able to read are also made, but they are more difficult to verify and, moreover, they must still be accompanied by a justification for correctness.
Task 1
Find the limit of the sequence (a n ) for which
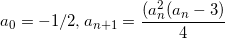
Answer
0
Decision
First we prove that the sequence converges. If a n <0 , then a n + 1 <0 , so it is bounded above. Compare an n and a n + 1 :
We see that for a n ∈ (-1; 0 ) the inequality a n <a (n + 1) holds, that is, the sequence increases. By the Weierstrass theorem, it has a limit. To find it, go to the limit in our recurrence relation:
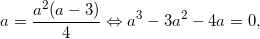
whence the limit can be one of the numbers 0, –1 and 4. It is easy to understand that this is 0.
We see that for a n ∈ (-1; 0 ) the inequality a n <a (n + 1) holds, that is, the sequence increases. By the Weierstrass theorem, it has a limit. To find it, go to the limit in our recurrence relation:
whence the limit can be one of the numbers 0, –1 and 4. It is easy to understand that this is 0.
Task 2
On a plane tiled with the same rectangles with sides 10 and 20 (the rectangles are adjacent to the sides), draw a random circle of radius 4. Find the probability that the circle has common points with exactly three rectangles.
Answer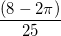
Decision
We will follow the position of the center of the circle. It is clear that it is possible to limit the consideration to the interior of one rectangle. It is easy to see that in order for a circle to intersect exactly three rectangles, two conditions must be met: (1) the distance from the center to the two nearest sides of the rectangle must be less than 4; (2) the distance to the nearest vertex of the rectangle should be greater than 4. Knowing this, we can draw a set of points that satisfy these conditions.
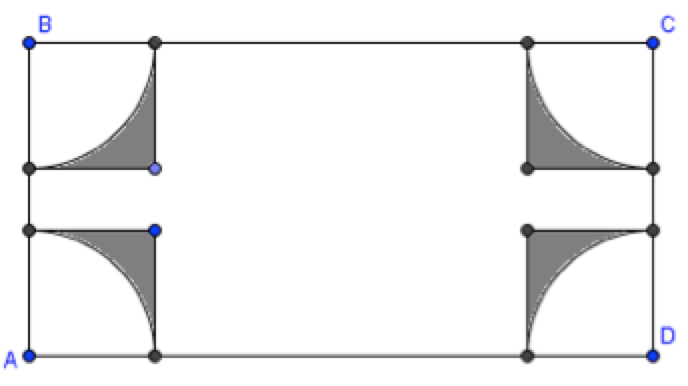
Therefore, the desired probability is
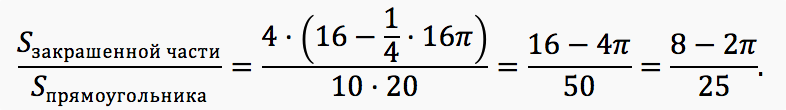
Therefore, the desired probability is
Task 3
Dima and Vanya take turns filling in a 2n × 2n matrix. Vanya's goal is to make the resulting matrix have an eigenvalue of 1, and Dima's goal is to prevent him. Dima goes first. Do any of them have a winning strategy?
Answer
With the right strategy, Vanya will win.
Decision
The resulting matrix A will have an eigenvalue of 1 if the matrix A - E is degenerate. To achieve this, Vanya can, for example, as follows. After Dima entered some element a ij , Vanya writes a new element a ik into the same line so that a ik- δ ik = - (a ij- δ ij ) , where δ ij is Kronecker's symbol . Then the sum of the numbers in each row of the matrix A - E will be equal to zero, that is, the matrix A - E will be degenerate.
Task 4
Find the determinant of the matrix A = (a ij ) , where
Answer
one
Decision
We use the formula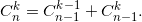 
We subtract the previous one from each row of the matrix, and then the previous one from each column. The resulting matrix will be:
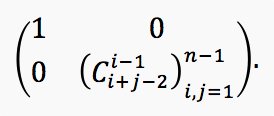
Continuing the argument by induction, we see that the determinant of the original matrix is equal to the determinant of the identity matrix, i.e. one.
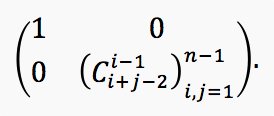
We subtract the previous one from each row of the matrix, and then the previous one from each column. The resulting matrix will be:Continuing the argument by induction, we see that the determinant of the original matrix is equal to the determinant of the identity matrix, i.e. one.
Task 5
Given two arrays of integers a [1..n] and b [1..k] , all elements of b are different. It is required to find a set of indices i_1 <i_2 <... <i_k , for which the set a [i_1], ..., a [i_k] is a permutation of the elements of the array b, and the difference i_k - i_1 is the minimum possible. The time limit is O (nk) (but maybe you can be faster), by memory O (n) .
Decision
This can be done in a single pass through the array a. Every time we encounter an element of the array b , we write it and its number in special arrays. At the same time, we support segment I in these arrays, on which we hope to find all the various elements of b . It is clear that if the next element of array a coincides with the first element of segment I, then I already clearly cannot be the shortest segment satisfying the condition of the problem, and we can shift its left end. If at the next step we understand that I contains all the various elements of b , then I is a candidate for an answer; in this case, we also shift its left end.
The O (n) estimate from memory is obvious. Estimation of O (nk) by complexity can be justified as follows: we do everything in one pass (from here n ) and at each step we should look for an element in the array b (from here k ). It is clear that the algorithm can be improved: if we first sort b and use binary search, we get O (n log k) . If we use perfect hashing, we can achieve O (n + k) complexity.
The O (n) estimate from memory is obvious. Estimation of O (nk) by complexity can be justified as follows: we do everything in one pass (from here n ) and at each step we should look for an element in the array b (from here k ). It is clear that the algorithm can be improved: if we first sort b and use binary search, we get O (n log k) . If we use perfect hashing, we can achieve O (n + k) complexity.
Task 6
In 2222, volleyball tournaments are held under the new system. They say that team A exceeds team B if A won against B or any team that won against B. Each pair of teams plays 1 time each. A draw is excluded by volleyball rules. The champion is announced a team that surpasses all other teams. (a) Prove that there will be a champion (b) Prove that there cannot be exactly two champions.
Decision
We agree that each team for the tournament gets points equal to the number of teams surpassed by it. First we prove the following simple lemma:
Lemma. Let team E not exceed team K. Then K scored more points than E.
Evidence. If E does not exceed K, then K won team E, as well as all the teams that team E. won.
Now let X be the team that team E has surpassed. If E won against X, then K also won against X. So, K surpasses X. If E won against team F, which won against X, then we note that K also won in F. So, K won in F, which won in X, that is, K exceeds X. Total, K surpasses all the teams that surpassed E, and even E in addition, that is, at least one team more than E The lemma is proved.
(a) Let A be the team that earned the maximum points. Let us prove that A is a champion. Suppose this is not the case, then there is team B, which A did not surpass. By the lemma, we get that B earned more points than A. Contradiction.
(b) Suppose we have two champions: A and B. They played with each other; Let, for example, A. won. Since B surpasses all other teams (and A in particular), B won against some team that beat A.
Suppose, to begin with, that there are teams that have won both A and B. Then you can show that the one of them (let's call her C), who scored the most points, will be the third champion. Indeed, let E be a team that has not surpassed S. Then, first, E won both A and B, and second, E earned more points than C. Contradiction.
Suppose now that there are no teams that have won both A and B. Consider the set of all such teams that have won A, but lost B. Note that it is not empty (see above). Among them, take the team with the highest score. Then using the lemma, we can establish that this team is the third champion.
Lemma. Let team E not exceed team K. Then K scored more points than E.
Evidence. If E does not exceed K, then K won team E, as well as all the teams that team E. won.
Now let X be the team that team E has surpassed. If E won against X, then K also won against X. So, K surpasses X. If E won against team F, which won against X, then we note that K also won in F. So, K won in F, which won in X, that is, K exceeds X. Total, K surpasses all the teams that surpassed E, and even E in addition, that is, at least one team more than E The lemma is proved.
(a) Let A be the team that earned the maximum points. Let us prove that A is a champion. Suppose this is not the case, then there is team B, which A did not surpass. By the lemma, we get that B earned more points than A. Contradiction.
(b) Suppose we have two champions: A and B. They played with each other; Let, for example, A. won. Since B surpasses all other teams (and A in particular), B won against some team that beat A.
Suppose, to begin with, that there are teams that have won both A and B. Then you can show that the one of them (let's call her C), who scored the most points, will be the third champion. Indeed, let E be a team that has not surpassed S. Then, first, E won both A and B, and second, E earned more points than C. Contradiction.
Suppose now that there are no teams that have won both A and B. Consider the set of all such teams that have won A, but lost B. Note that it is not empty (see above). Among them, take the team with the highest score. Then using the lemma, we can establish that this team is the third champion.
Task 7
Calculate the integral
Answer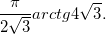
Decision
We denote the desired integral by I. We make the change of the variable:
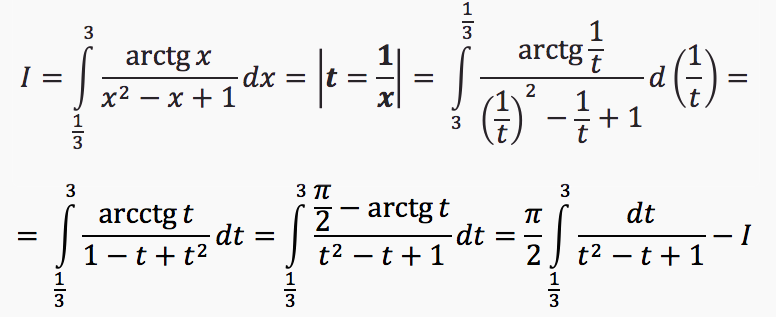
From here
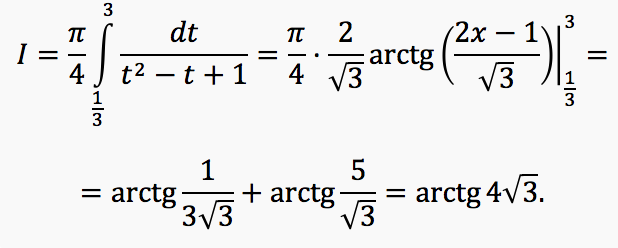
This integral is already taken directly.
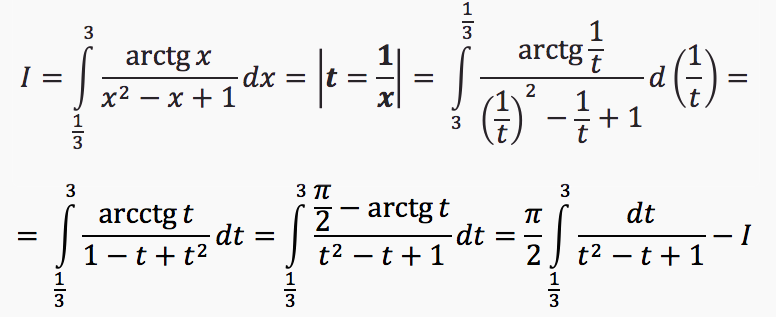
From here
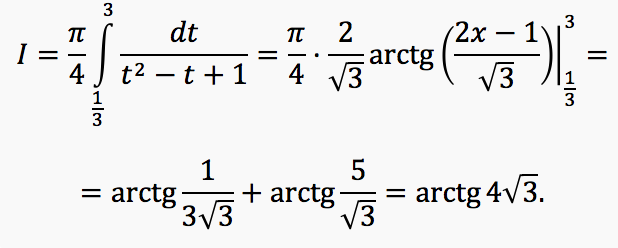
This integral is already taken directly.
Task 8
On the plane there is a broken line with n links. The length of each link is 1, the oriented angle between adjacent links with equal probability is α or –α . Find the expected value of the square of the distance from its starting point to the end.
Answer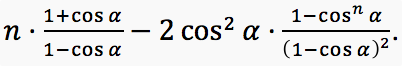
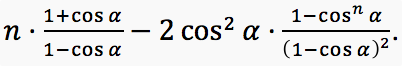
Decision
We introduce a coordinate system on the plane so that the first link of the polyline is directed along the Ox axis. Let α n be the oriented angle between the (n + 1) -th link of the polyline and the first link of the polyline (ie, the axis Ox). Then α 0 = 0, α (n + 1) = α n + ξ (n + 1) α , where ξ n is a random variable taking values of ± 1 with a probability of 1/2. Note that the projections on the Ox and Oy axes of the k-th link of the polyline are cos α (n-1) and sin α (n-1), respectively. Then the square of the distance from the beginning of the polyline to its end is equal to
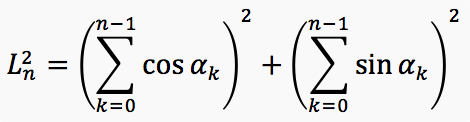
Our task is to find the expectation of this random variable. We have:
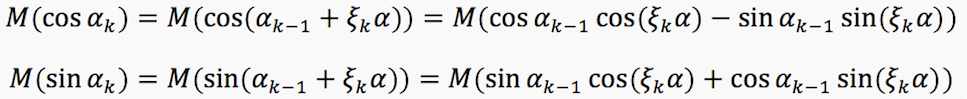
Using the fact that sin α 0 = 0 and cos (ξ k α) = cos α (due to the oddness of the cosine), by induction we get that M (cos α k ) = cos k α ,M (sin α k ) = 0 . Next we find the mathematical expectation of works. Let m≥k . Using induction on (m - k), we can prove that
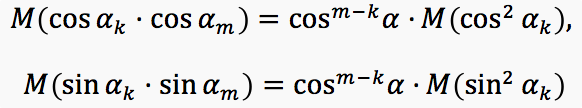
Consequently,
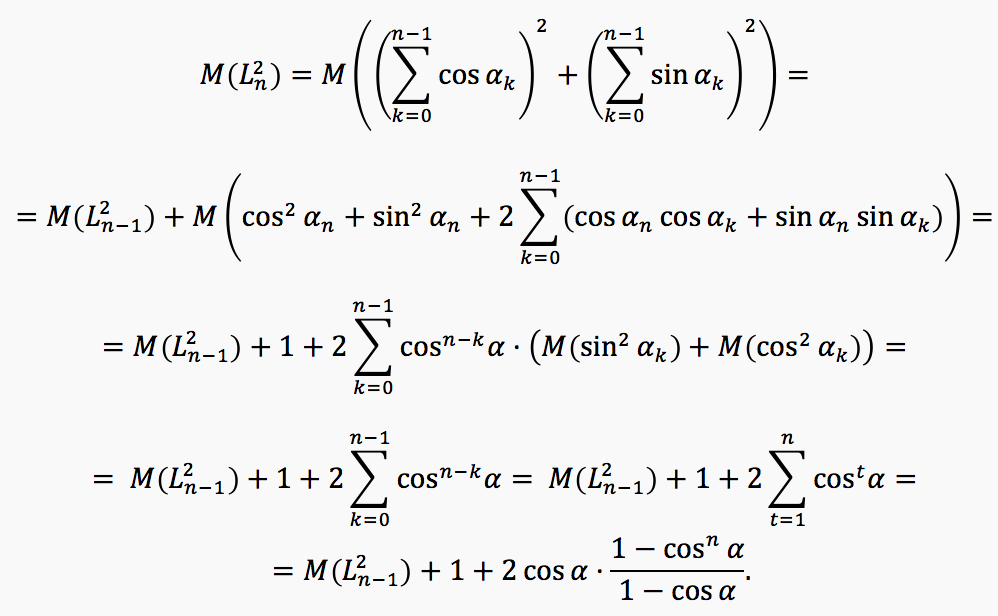
From here it is not difficult to deduce the answer.
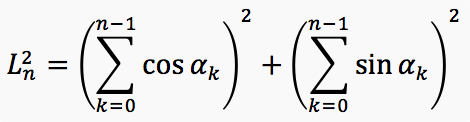
Our task is to find the expectation of this random variable. We have:
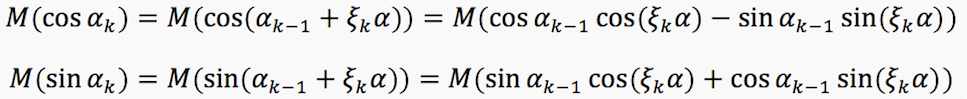
Using the fact that sin α 0 = 0 and cos (ξ k α) = cos α (due to the oddness of the cosine), by induction we get that M (cos α k ) = cos k α ,
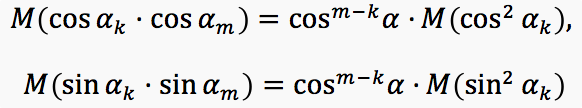
Consequently,
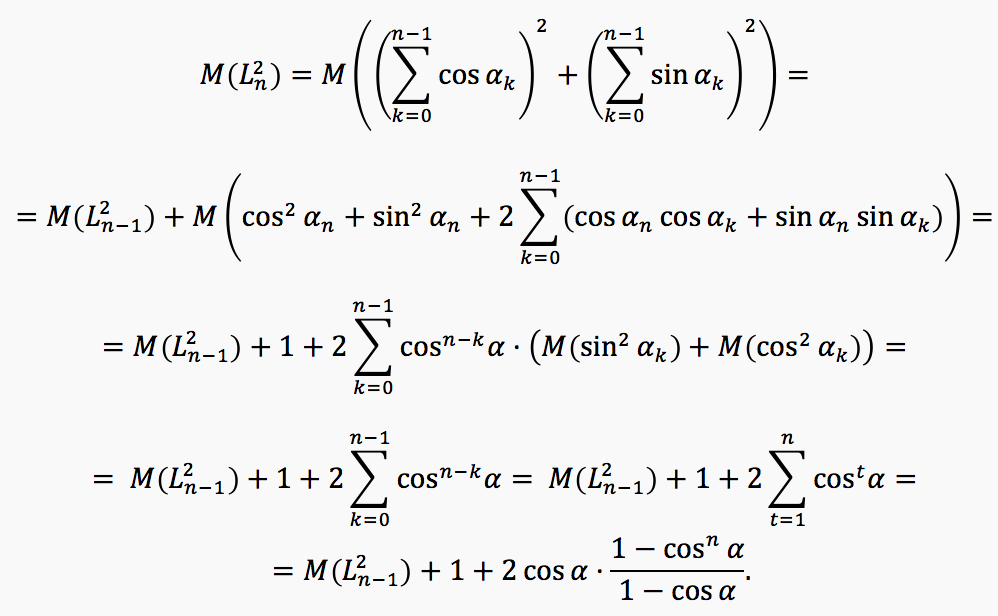
From here it is not difficult to deduce the answer.
Source: https://habr.com/ru/post/262543/
All Articles