2 Pi or not 2 Pi - that is the question

Translation of Giorgia Fortuna post " 2 Pi or Not 2 Pi? ".
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

Three months ago, the world (or at least the world of geeks) celebrated Pi Day (03.14.15 ...). Today (6/28 - June 28, 2015) is another mathematical day - day 2π, or Tau day (2π = 6.28319 ...).

Some say that the day of tau is really the day for celebration, and that τ (= 2π), and not π, should be the most important constant. It all started in 2001 with the opening remarks of the famous essay by Bob Palais , a mathematician from the University of Utah:

“I know that some will consider it a blasphemy, but I believe that π is a mistake.”

This caused in some circles the celebration of the day of tau - or, as many say, the only day on which two pi (horns) can be eaten (2pies≈2π is a pun in English).
')
But is it true that τ is a better constant? In today's world, this is quite easy to check, and Wolfram Language makes this task even easier (indeed, the recent post on Michael Trott ’s blog about dates in pi , inspired by Stephen Wolfram's post about celebrating the centuries-old pi day , actively involved Wolfram Language). I began by looking at 320,000 preprints on arXiv.org to see how many formulas actually contain 2π compared to those that simply contain π or π with other factors.

Here is a cloud of some formulas, built using the WordCloud function, containing 2π:



I found that only 18% of the formulas in question contain 2π, which means that switching to τ is not the best choice.

But why then do supporters of using τ think that we should move on to the use of this new symbol? One reason is that using τ should make trigonometry easier to learn and understand. After all, in trigonometry, we use not angles, but radians, and the circumference contains 2π radians. This means that a quarter of a circle corresponds to 1 / 2π radians, or π / 2, and not a quarter of something! This injustice can be eliminated by introducing the symbol τ , and then each part of the circle will correspond to the same part of τ . For example, a quarter of a circle would correspond to the angle τ / 4.



Personally, my use of the number π does not cause any strong negative feelings, and frankly, I do not think that using τ would allow students to learn trigonometry more quickly. Let's remember the two most important trigonometric functions - sine and cosine. Perhaps the most important in the study of trigonometry formulas - sin = cos (2π) = 1, and sin ( ) = cos (π) = –1. I not only always preferred to use cosine because its values ​​are easier to remember (there are no fractional values ​​in π and 2π), but I also always remembered that sine and cosine are distinguished by the fact that one function accepts nonzero values ​​at points that are multiples of π and the other takes nonzero values ​​in the fractional parts of π. If you use τ , then we lose this symmetry, and we will have the equations sin = cos ( τ ) = 1 and sin = cos = –1.

Given the above, it turns out that the use of τ or π is a matter of personal preference. This is a fair conclusion, but we need a more rigorous approach to determine which of the constants is more useful.

Even the approach that I was guided by at the beginning can lead to wrong conclusions. In the Tau Manifesto, Michael Hartl gives some examples of places where you can often find 2π:



Indeed, all these formulas would look simpler if we used τ . However, these are just six formulas from the huge number that scientists regularly use, and as I mentioned earlier, not too many mathematical expressions contain 2π. However, it is possible that formulas that do not contain 2π will be simpler if written in terms of τ . For example, the expression 4π² is simply written as τ ².

Therefore, I returned to the scientific articles to find out whether using τ instead of 2π (and τ / 2 instead of π) would make the formulas simpler. For example, here are those that will become simpler using τ :



Here are some of those that will not:



Let me explain what I mean by a simpler form of an example: if I take the part containing π in the lower left formula of the table with Tau manifest formulas (see above):



I can replace π with τ / 2 using the ReplaceAll function and get:



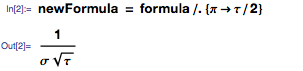
Looking at these two expressions, you can see that the second is simpler. And it's not about intuition - the second is just less characters. For greater clarity, we can consider the corresponding tree graphs through the function TreeForm :



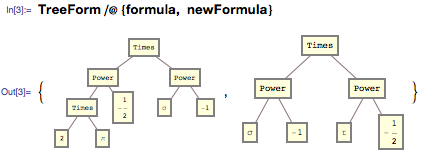
To obtain a numerical representation of their differences, we can use the number of branches of the tree, which correspond to the number of symbols in the original formulas:



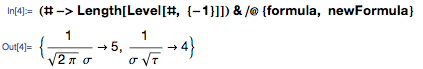
To determine whether a formula is simplified as a result of using τ , I calculated the complexity of each formula (which is determined by the number of tree branches) containing π for formulas from the articles, depending on which of the constants is π or τ . For greater accuracy, I first deleted all expressions that were equal to or equivalent to π or 2π. I felt that it would be unfair to take them into account, because they are often found on their own, outside formulas. Then I compared the cases when the use of τ simplified the formula with those when it was complicated, and only 43% of the formulas became simpler using τ , that is, in more than half of the cases, the use of τ complicates the formula. In other words, it follows from this comparison that we must continue to use π. However, this is not the end of the story.

I noticed this: if the expression becomes more or less complex, it means that the number of branches is less than 40. In fact, if you look at the percentage of formulas that become easier using π or τ and have a number of branches less than a certain value , then you will see the following picture:



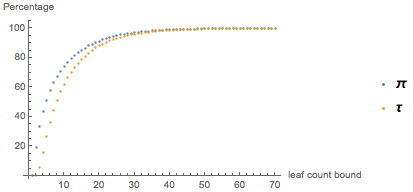
The x- axis represents the upper limit of the number of branches. From this it follows that for almost all formulas, their complexity depends on the choice of a symbol only if the number of branches is less than 50.

A more important observation is that as the complexity of the formula increases, the situation changes dramatically. Even if you choose formulas with complexity greater than 3, like the formula considered earlier then only 48% of the formulas will become simpler using π versus 52% for τ . The graphs below show how the percentages of formulas that are simpler using π or τ vary depending on the complexity:



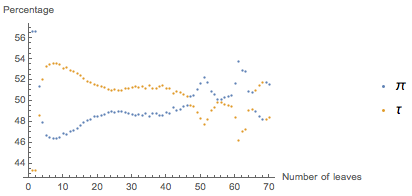
As you can see, with more than 48 branches, the graphics start to behave erratically. This is a consequence of the fact that only 0.4% of the sampling formulas have a complexity of more than 50. We cannot say anything particularly concrete about them, and past experience tells us that we don’t really need it.

And from this graph also follows that in everyday life and for some expressions that are more complicated than something like , in order to simplify expressions, we definitely should use τ . But there is another point that I did not touch. What about different application areas?

Perhaps in physics, formulas will look easier with τ , but not in other areas. Initially, I included articles from various fields in the search; However, I did not check whether formulas containing π belong to one or another field of knowledge, and also whether formulas that are easier to use with τ belong to some limited subset of domains. In fact, if we consider only mathematical articles, the result will be as follows:



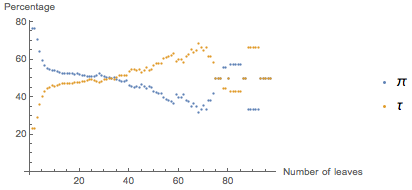
It turns out that only 23% of all formulas become simpler using τ , and even then only for fairly complex expressions. Here is something like this:



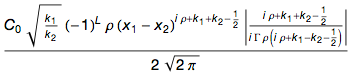
It can be written more easily with τ , however, most of such expressions are very rare. It turns out that either scientists from different areas should use different conventions depending on their specific field of formula, or everyone should switch to using τ , although in fact for some areas it does not make much sense. In the end, democracy implies the satisfaction of the majority, and it is impossible to please everyone without exception.

Nevertheless, the above formula contains something else that I would like to focus on. So it looks like with τ :



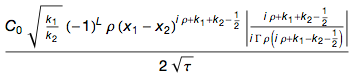
Let the expression really be easier written in τ , but this improvement is so insignificant that it becomes negligible. Consider, for example, these two expressions, along with the numbers of their branches:



And the corresponding expressions in τ :



The first formula is simpler in τ , but the number of branches becomes only 1/13 less in comparison with the initial number, while the second expression is easier written to π, and after replacing it, the complexity increases by 1/6. In other words, the improvement in the first case was 1/13, and in the second -1/6 (the minus sign indicates deterioration). Mean vector is -0.044 is a negative number, which means that using τ in these two expressions makes the total vector 0.044 worse.

This vector approach differs from the previously used approach, which did not take into account the size of the equation. It considers the number of improvements, not the number of simplified expressions, and this turns the previous conclusions upside down. I obtained these vectors for formulas in which complexity is bounded below - all the same as in the previous example. It turns out that the overall improvement in replacing π with τ decreases with increasing complexity:



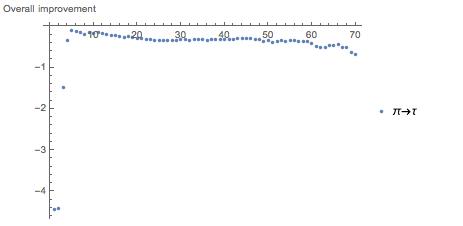
and the least deterioration of -0.04 is achieved with complexity 5. As you can see, the overall improvement is always negative; This means that even a larger number of formulas have a shorter notation in terms of τ (depending on the region), but on the whole the sum of all the “simplifications” of the formulas is outweighed by all the “complications”.

As a result of all this research, I have formed such a position: I think we should be satisfied with our old friend π and not switch to the use of τ .

I have two final remarks. The first is that if we lived in a world where τ is used more actively, the conclusion would be completely opposite. If our expressions were already written in terms of τ , and we investigated the transition to the use of π and the questions of simplification, then our graph of the sums of vectors would look like this:



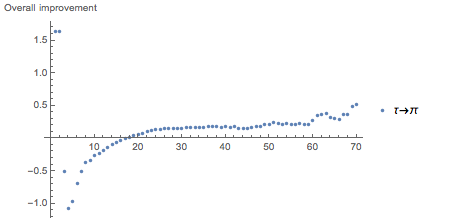
Such a difference is explained by the fact that the vectors used for plotting depend on the initial difficulties, and therefore change as they change.

From this it follows that for the majority of formulas that have complexity more than two and less than 18, the improvement from replacing τ with π will be negative. Unfortunately for supporters of τ , we still live in the world π.

The second remark, which Michael Trott brought me, is that 2/3 of the formulas specified in the Tau Manifesto (green table at the beginning of the post) contain not just 2π, but the complex expression 2π i. This suggests that, perhaps, the very posing of the question, which I tried to answer, is incorrect. Perhaps the best wording would be the following: would it make sense to introduce a new symbol τ for the complex number 2π i ?

This new designation will also require replacing π i with τ / 2, but this will not affect the complexity of π i . In general, formulas containing π i will either reduce or keep their complexity. Here is a cloud of formulas that will become simpler:



So they will look after the substitution of 2π i on τ :



One might argue that the percentage of improvement of the formulas will not be high enough, and the transition from 2π i to τ is unjustified. However, the facts say the opposite: of all formulas containing π i , 75% will become simpler, and the remaining 25% will retain their level of complexity — that is, not a single formula will become more complicated. This is a weighty argument, but I am not in a position to translate this idea; however, I believe that equality τ = 2π i is more promising (and less historically difficult) than τ = 2π.

Regardless of your opinion on τ , I hope you had a great Tau day. Enjoy the present day of two pi (horns) - imaginary or whatever.