The magic of tensor algebra: Part 7 - The final rotation of a rigid body. Rotation tensor properties and method for calculating it
Content
- What is a tensor and what is it for?
- Vector and tensor operations. Ranks of tensors
- Curved coordinates
- Dynamics of a point in the tensor representation
- Actions on tensors and some other theoretical questions
- Kinematics of free solid. Nature of angular velocity
- The final turn of a solid. Rotation tensor properties and method for calculating it
- On convolutions of the Levi-Civita tensor
- Conclusion of the angular velocity tensor through the parameters of the final rotation. Apply head and maxima
- Get the angular velocity vector. We work on the shortcomings
- Acceleration of the point of the body with free movement. Solid Corner Acceleration
- Rodrig – Hamilton parameters in solid kinematics
- SKA Maxima in problems of transformation of tensor expressions. Angular velocity and acceleration in the parameters of Rodrig-Hamilton
- Non-standard introduction to solid body dynamics
- Non-free rigid motion
- Properties of the inertia tensor of a solid
- Sketch of nut Janibekov
- Mathematical modeling of the Janibekov effect
Introduction
In this article we will continue the topic begun by the previous publication . Last time we, using tensors, revealed the nature of the angular velocity and obtained equations of a general form, allowing it to be calculated. We came to the conclusion that it is naturally derived from the rotation operator of the body-related coordinate system.
And what's inside this operator? For the case of Cartesian coordinates, it is easy to obtain rotation matrices and it is easy to detect their properties by associating with them some method of describing the orientation of the body, for example, the Euler or Krylov angles. Or the vector and the angle of the final rotation. Or quaternion. But this is for Cartesian coordinates.
')
Starting to talk about tensors, we renounced Cartesian coordinates. So good is the tensor notation, because it allows you to make equations for any convenient coordinate system, without focusing on its properties. And the problem is that for, for example, oblique coordinates, the rotation matrix, even for a plane case, is extremely complex. I had enough to check their appearance for a simple turn in the plane.
So the task of this article is to look at its properties without looking inside the rotation tensor and obtain a tensor relation for its calculation. And once the task is set, we will begin to solve it.
1. Properties of the rotation coordinate system tensor
In order to return to the mechanics of a free rigid body, it is necessary to understand what the rotation tensor is. The properties of a tensor are determined by the set of its components and the ratio between them. Since the turning tensor is a second-rank tensor and its components are represented by a matrix, then, not to the detriment of the general theme of the cycle, I will lead the presentation of this section using the term “matrix”. The usual “pointless” notation of the matrix product will be written with a dot, because in the framework of the algebra of tensors we are dealing with a combination of a tensor product with convolution. However, a reservation is also needed here - having criticized myself for the incorrect use of the term "convolution", I missed the moment that under the convolution is often understood its combination with tensor multiplication. At the same time they say, for example, “we turn the vector with the Levi-Civita tensor and we get ...”, meaning just the operation of the inner product.
So, consider the main properties of the rotation matrix
- The transformation of the rotation of the metric tensor is the identity transformation
- The determinant of the rotation matrix is equal to one
- The inverse transform matrix is similar to the transposed direct transform matrix.
- If a
, the matrix of algebraic complements and the union matrix constructed from
similar to this and its transposed matrix, and the similarity transformation is the metric tensor
The consequence of this property is the equality of traces of the listed matrices. - If a
then the eigenvalues of the rotation matrix are equal to unity and have the form
Where - If a
Is the eigenvector of the rotation matrix corresponding to the complex eigenvalue, then the following relation is true
Corollary: real and imaginary parts of an eigenvectorcorresponding to a complex eigenvalue are orthogonal vectors
Where.
I will not give evidence of the properties in the main text - the article already promises to be voluminous. These proofs are not too complicated, but for those interested in them, the following spoiler is made.
Proof of properties 1 - 6 for the inquisitive and meticulous reader
Properties 1 and 3 we proved in the previous article . Property 2 is proved from property 1 trivially, based on the properties of the determinant of the matrix product

%5E2%20%3D%201)

Property 4 follows from the analytical method for calculating the inverse matrix. then
then


Where - union matrix (transposed matrix of algebraic complements). Transposing (1), using the symmetry of the metric tensor, we obtain
- union matrix (transposed matrix of algebraic complements). Transposing (1), using the symmetry of the metric tensor, we obtain
%5ET)
%5ET)

Where - a matrix composed of algebraic complements of the rotation matrix. Relations (1) and (2) are similarity relations. The traces of such matrices are the same.
- a matrix composed of algebraic complements of the rotation matrix. Relations (1) and (2) are similarity relations. The traces of such matrices are the same.
%20%3D%20%5Cmathop%7B%5Crm%20tr%7D%5Cmathbf%7BB%7D)
Let us prove property 5. Let - eigenvalue of the rotation matrix to which the eigenvector corresponds
- eigenvalue of the rotation matrix to which the eigenvector corresponds  . Then
. Then

Multiply this expression by the inverse transform matrix on the left.

subject to property 3

We perform complex conjugation, given that the rotation matrix and the metric tensor have real components and their conjugation is reduced to transposition
%5E%7B*%7D)
%5E%7BT%7D)

The last expression is multiplied on the right


Finally we have the equation
%5Cmathbf%7Bu%7D%5E%7B*%7D%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cmathbf%7Bu%7D%20%3D%200)
which is valid only when

i.e

To calculate the eigenvalues we make the characteristic equation
%20%3D%200)
calculating the determinant, we arrive at the general form of this equation (for a matrix of dimension (3 x 3))
)
Enter the notation
)
We decompose (4) into factors
%5Cleft(%5Clambda%5E2%20%2B%20%5Clambda%20%2B%201%20%5Cright%20)%20-%20s%20%5C%2C%20%5Clambda%20%5Cleft(%5Clambda%20-%201%20%5Cright%20)%20%3D%200)
%5Cleft(%5Clambda%5E2%20-%20%5Clambda%20%5Cleft(s%20-%201%20%5Cright%20)%20%2B%201%20%5Cright%20)%20%3D%200)
where we immediately get

The remaining pair of roots is found by solving a quadratic equation
%5E2%20-%201%7D)
We introduce a replacement

which is legitimate, because, putting the roots, in the general case complex-conjugate, according to the Vieta theorem, we have

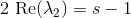
or by absolute value
%5Cright%7C%20%3D%20%5Cleft%7Cs-1%5Cright%7C)
Because%5Cright%7C%20%5Cle%20%5Cleft%7C%5Clambda_2%5Cright%7C%20%3D%201)
then obviously

Making the replacement, we finally calculate

The proof of property 6 will be carried out based on the expression

obtained in the proof of equality to a unit of modulus of an eigenvalue. Now, instead of complex conjugation, we transpose it, taking into account the properties of the transposition of the matrix multiplication

Multiply the resulting expression by on right
on right


Now multiply the resulting equation by the number of complex conjugate eigenvalue, given that its modulus is equal to one


Finally we arrive at the equation
%20%5C%2C%20%5Cmathbf%7Bu%7D%5ET%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cmathbf%7Bu%7D%20%3D%200)
in which the bracket, due to the complexity of the eigenvalue, is not equal to zero, since
)
Then fair

The corollary of this property is proved by simple multiplication.
%5ET%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cleft(%5Cmathbf%7Bu%7D_%7B%5C%2Cr%7D%20%2B%20i%20%5C%2C%20%5Cmathbf%7Bu%7D_%7B%5C%2Ci%7D%20%5Cright%20)%20%3D%20%5Cleft(%5Cmathbf%7Bu%7D_%7B%5C%2Cr%7D%5ET%20%2B%20i%20%5C%2C%20%5Cmathbf%7Bu%7D_%7B%5C%2Ci%7D%5ET%20%5Cright%20)%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cleft(%5Cmathbf%7Bu%7D_%7B%5C%2Cr%7D%20%2B%20i%20%5C%2C%20%5Cmathbf%7Bu%7D_%7B%5C%2Ci%7D%20%5Cright%20)%20%3D)

Equating real and imaginary parts to zero


The last equations imply the required orthogonality and equality of the modules. and
and 
Property 4 follows from the analytical method for calculating the inverse matrix.
Where
Where
Let us prove property 5. Let
Multiply this expression by the inverse transform matrix on the left.
subject to property 3
We perform complex conjugation, given that the rotation matrix and the metric tensor have real components and their conjugation is reduced to transposition
The last expression is multiplied on the right
Finally we have the equation
which is valid only when
i.e
To calculate the eigenvalues we make the characteristic equation
calculating the determinant, we arrive at the general form of this equation (for a matrix of dimension (3 x 3))
Enter the notation
We decompose (4) into factors
where we immediately get
The remaining pair of roots is found by solving a quadratic equation
We introduce a replacement
which is legitimate, because, putting the roots, in the general case complex-conjugate, according to the Vieta theorem, we have
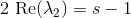
or by absolute value
Because
then obviously
Making the replacement, we finally calculate
The proof of property 6 will be carried out based on the expression
obtained in the proof of equality to a unit of modulus of an eigenvalue. Now, instead of complex conjugation, we transpose it, taking into account the properties of the transposition of the matrix multiplication
Multiply the resulting expression by
Now multiply the resulting equation by the number of complex conjugate eigenvalue, given that its modulus is equal to one
Finally we arrive at the equation
in which the bracket, due to the complexity of the eigenvalue, is not equal to zero, since
Then fair
The corollary of this property is proved by simple multiplication.
Equating real and imaginary parts to zero
The last equations imply the required orthogonality and equality of the modules.
Why do we need to know about the properties of the rotation tensor?
First, I have completely formulated them, so that the reader can see how the rotation matrix of the curvilinear coordinate system differs from the rotation matrix of the Cartesian system. Practically nothing more, the properties of these matrices are similar. If in the above expressions we put the matrix of the metric tensor of the unit matrix, then we obtain the property of an orthogonal rotation matrix, about which one can read, for example, D.Yu. Pogorelov . Actually this book told me where to dig, to consider the task in general.
Secondly, and this is important, we will prove that the eigenvectors and eigenvalues of these matrices have a mechanical meaning. First we prove the lemma
Let beIs the eigenvector corresponding to the real eigenvalue of the rotation tensor, and
- complies
, and
. Let, also, vectors
and
real and imaginary part
. Then vectors
,
and
form a trio of orthogonal vectors
Property 6 already tells us about orthogonality.
By defining eigenvectors
Multiply (3) on the left by
Given property 3 we can say that
In addition, from (2) directly follows
Given (6) and (5) we convert (4)
The expression in parentheses is a nonzero complex number. Assertion (1) is true and the vectors under consideration form an orthogonal triple.
The lemma proved by us is needed to show that the rotation tensor, which we consider in arbitrary coordinates, satisfies the well-known Euler's theorem on finite rotation.
2. Euler's theorem on the final turn
Studying the rotation tensor, we realized that an orthogonal triple of vectors is directly connected with this tensor
This vector remains fixed when turning! And when turning the body, the motionless remains ... the axis of rotation. Means vector
For any body that has one fixed current and occupies an arbitrary position in space, there is an axis passing through a fixed point, by rotating around which the body can be moved to any other desired position at the final angle.
Identity (7) gives us a hint about where to look for this axis of rotation - it passes through the eigenvector of the rotation tensor corresponding to its real eigenvalue. Check it out by proving the theorem
The coordinate system associated with the body can be aligned with the base coordinate system by rotating around a vectorat an angle
counterclockwise if the vectors
form the top three, and at an angle
if these vectors form the left three
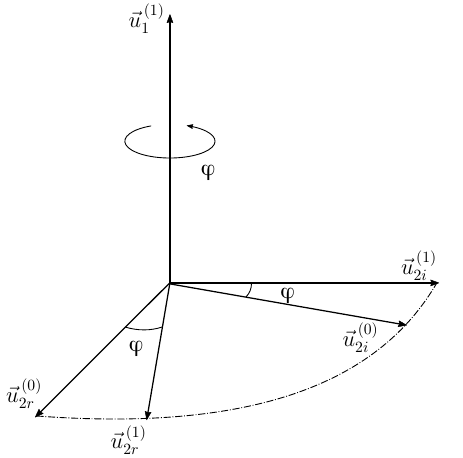

Fig 1. To the proof of the theorem on the final turn
Rotate body-related coordinate system by angle
Expressions (8) and (9) are obtained by analyzing the final rotation. On the other hand, the chain of transformations follows from the definition of the eigenvector and the properties of the rotation operator
Equating the real and imaginary parts (10), we obtain
Comparing (8) and (11), (9) and (12), we conclude that applying the rotation operator to vectors leads to their rotation around the axis
I must say, our results look pretty impressive - after all, not knowing about the insides of the rotation tensor, we investigated everything (at least its practically significant properties). And we are not particularly interested in the insides of specific rotation tensors, our main task is to learn how to calculate this tensor, so that it provides a rotation around the axis we need at the required angle
3. Expression of the rotation tensor through the parameters of the final rotation. Rodrigue Formula
Consider the final rotation of an arbitrary vector. In the base coordinate system, its position corresponds to
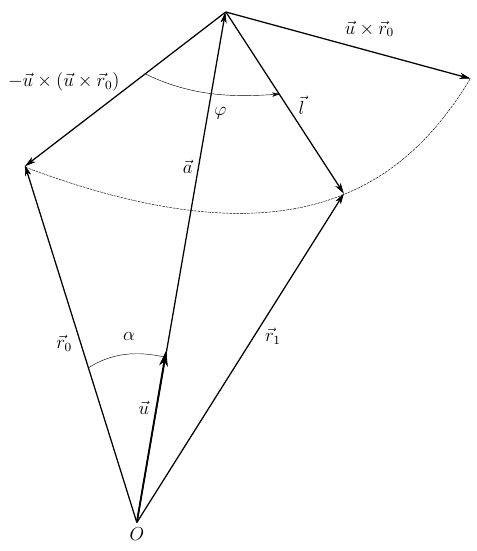
Fig. 2. The final rotation of an arbitrary vector
From Figure 2, the vector relationship is obvious.
Where
Vector
On the other hand, the following vectors have the same module
mean vector
Now, the written vector relations will be represented in the tensor component form
and we introduce two antisymmetric tensors
Given which you can write
Convolution of tensors (16) and (17) on a common index, we execute by writing them through the matrix of components
It is easy to see that (19) is equivalent
Convert (18) with (20)
From (21) we obtain the expression for the rotation operator
Where
- antisymmetric tensor of rank (0,2), generated by the ort of the axis of rotation.
or, in component form
Expressions (22) and (23) are called the Rodrigues rotation formula. We obtain them for a coordinate system with an arbitrary nondegenerate metric.
Conclusion
All of the above was considered for one single purpose - to obtain the expression of the rotation operator for an arbitrary coordinate system. This will allow us to express through (23) the tensor and pseudovector of angular velocity, and then angular acceleration. After this, we will choose the parameters characterizing the orientation of the solid in space (these will be Rodrig – Hamilton parameters, yes, we will talk about quaternions) and we will write down the equations of motion of a solid body in generalized coordinates. , , , .
Thanks for attention!
To be continued…
Source: https://habr.com/ru/post/262263/
All Articles