Using potential fields in real-time strategy scenarios
Implementing unit behavior in RTS games can be a major problem. The computer often controls a huge number of units, including those belonging to the player, which must move in a large dynamic world, simultaneously avoiding collisions with each other, looking for enemies, defending their own bases and coordinating attacks to destroy the enemy. Real-time strategies work in real time, which makes tracking planning and navigation quite difficult.
This lesson describes a game flow planning and unit navigation method that uses multi-agent potential fields. It is based on works under the numbers [1, 2, 3]. (See the end of the article links to the materials used)

')
PP (Potential Field) has a number of similarities with influence maps. Influence cards are often used to determine whether a zone in the game world is under the control of a player or enemies (in the range of weapons or movement), or is it a zone that is not currently controlled by anyone (nobody's land). The idea is to put positive values on the cells under the control of the player, and negative values - under the control of the enemy. Smoothly reducing the value to zero, we will create a map reflecting the influence of our own and enemy units in the zone. The figure below shows an example of an influence card with one of its own and one enemy unit.

Potential fields work in a similar way - a charge is put on the position of interest in the game world and generates a field that gradually drops to zero. The charge can be attractive (positive) or repulsive (negative). Please note that in some literature on potential fields negative charges attract and vice versa. In this lesson, positive charges are always repulsive. The figure below shows a simple game world with some impassable territory (brown), an enemy unit (green) and a destination of the unit (E). Attracting charge is located at the destination.

The charge generates a field that spreads across the game world:

And decays to zero:

In the illustration above, the attracting field spread around the destination point “E”. The idea is to allow the green unit to move to the positions with the most attracted values and eventually find the way to the destination point. To make it work, we also need to deal with the obstacles in the game world, in this case with the mountains (cinnamon zones). If we make the mountains generate small repulsive fields and combine them with attracting fields (from the picture above), we get a resultant field that can be used for navigation. Since units always move to the next position with the most attractive value, we will go around the mountains if there is another way.

The same idea is used for other obstacles. The picture below added two more of their units (white). They generate small repulsive fields, which are again added to the resulting field.

Thus, our green unit will bypass these units to avoid collisions. Now we have the final path for our unit. A unit can move from its current position to its destination and will bypass all obstacles without using any path finding algorithm.

One of the most important advantages of using potential fields is the ability to handle dynamic game worlds. Since units (agents) move only one step at a time, instead of generating a full path from A to B, there is no risk that the path will become unavailable due to changes in the game world. Finding a path in a dynamic world can often be difficult to implement and require a large amount of resources to calculate. When an approach based on potential fields is used, the solution of the problem comes by itself, automatically. Of course, you need to be careful when implementing the software system to not forget to make updating potential fields as effective as possible. (More on this later).
Another important advantage is the ability to create complex behavior just by playing with the shape settings of the generated fields. Instead of linear attenuation to zero, we can use nonlinear fields. If we, for example, have shooting units like tanks in our army, we don’t want tanks to move too close to enemy units, but surround them at the right distance (for example, at a distance of their shooting range). This behavior can be achieved by placing a zero charge at the location of an enemy unit, generating an increasing field with the most attracted point at the firing range, and then decaying to zero. The picture below shows an example with two tanks (green) moving into an attack on an enemy unit (red), generating a non-linear PP.

An example of an equation for how such a field can be generated:

Here, W1 is the value for changing the relative field strength. D is the maximum firing range and R is the maximum detection range (whence our agent sees an enemy agent)
Another behavior that is easy to implement is “kicked-run”. First, the unit approaches the maximum attack distance.

After the attack, our unit must reload its weapon and retreats from the enemy unit until it is ready to fire again.

During the retreat phase, all enemy units generate a strong repulsive field with a radius of maximum firing range of the unit. This is an example of how specific potential fields can be active or inactive, depending on the internal state of the agent controlling this unit. An inactive field is simply ignored when the resulting potential field is summed.
The picture below is a screenshot of our bot, based on the PP for the ORTS engine. The left side of the image is a 2D view of the current state of the game. It shows our tanks (green circles), going to attack enemy bases (red squares) and units (red circles). Brown and black areas - impassable territory (mountains). The potential field of this game state is shown on the right side of the image. As in the other pictures from this lesson, the blue zones are the most attractive. The bright lines are the attacks of our tanks. The PP-view clearly shows how our units surround the enemy at the maximum distance of the shot, while at the same time avoiding collisions with each other and the terrain. The behavior of the enemy environment works perfectly and was probably one of the key ones in our success of the 2008th year at the ORTS tournament.

While we were developing our bot for ORTS, we found one thing - a completely different behavior, when the summation of the potentials of enemy units generated at each point was compared with just the highest potential of the enemy unit at that point. In the figure below, the potentials generated by the three enemy units are summed and added to the resulting field. Thus, the greatest potential is right in the center of the enemy unit cluster (circled in red), and our units are very eager to attack the enemies at their most powerful points.

The solution was not to summarize the potentials, but instead to take the greatest potential at a point from all units. In the latter case, the highest potential around enemies at an acceptable distance (shown by red lines).

With a good plan and implementation of the PP system, the cost of resources for the calculation will not exceed the traditional solutions based on the algorithm A *. Our ORTS bot used the least amount of CPU resources in comparison with two other bots running on path finding algorithms from the 2007 tournament. However, we note that it is difficult to accurately calculate the use of the CPU, due to the fact that the winning bot uses more resources at the end of the game, as it has more units under control. Multithreading also complicates the task of calculating the required CPU resources. The comparison was made by comparing the total amount of CPU resources used by each client process in the Linux environment for 100 games. At the very least, we can conclude that the bot was good within the time frame of 0.125 seconds used in ORTS.
To improve performance, we divided the PP into three categories:
We experimented with two main architectures for generating PP ...
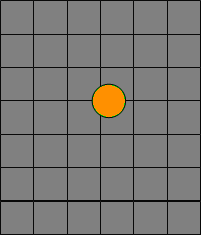
The field generated by each type of object was calculated in advance and stored in static arrays in the header file. During the execution of the program, these fields were simply added to the general software in the desired position. To make this possible, the game world was divided into tiles, in our case each tile consisted of 8x8 points of the game world. This approach showed insufficient detailing and the bot performed poorly (2007 of the ORTS tournament). Since the game world was divided into significantly larger tiles, we were faced with the problems of deciding which tile (which tiles) an object is occupying. Suppose an object (an orange circle) and a base (an orange square). What tiles (gray squares) does our green unit occupy and what tiles should the base occupy?
This approach may be suitable for games like Wargus, which use a less detailed tile navigation system.

Potentials generated at a point are calculated in real time by calculating the distance between the point and all the nearest objects, passing each distance as a variable to a function and then calculating the potential. This approach actually uses less CPU resources in our bot than pre-generated fields.
Thanks to:
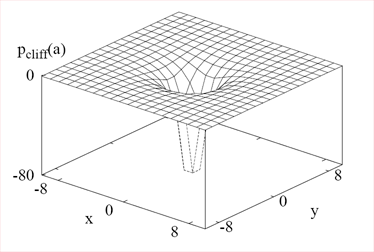
This approach was used in the second version of our bot (ORTS 2008 tournament). An example of the formula PP (with 2D and 3D graphs), used to calculate the potential generated by a cliff at a point with a distance "a" from the cliff.


One of the most common problems with PP is the problem of local optimum. In the picture below is an example when this problem appears. Destination "E" generates a circular field, which is blocked by the mountain. The unit moves to the positions with the highest potentials and ends at the largest where it currently stands. Unit stuck.

We solved this by using a trace similar to the pheromone trace described in [4]. Each agent controlling a unit adds a trace in the last N positions visited by the unit, as well as to the current position of the unit. The trail generates a light repulsive potential and “pushes” the unit forward. See how a track pushes a unit around a local optimum (yellow line) and the unit can find the way to the destination point.

But even with the traces there is a risk that the unit will get stuck in situations like the one in the picture below.

This can be solved by filling in the voids:

Below we have compiled criticism against decisions based on PP from our point of view:
The PP has problems like a local optimum that are difficult to solve. With the use of the trace, most local optima can be solved. The PP has problems in very difficult terrain; in these cases, methods of finding a path show themselves better. The power of PP in the processing of large dynamic worlds with large open spaces and the least difficult terrain. This is the case for many RTS games of today.
Solutions based on PP require a lot of resources. We have shown in our work that solutions based on software can be implemented with the same or even better efficiency as the methods of finding the path. Efficiency can be a problem, but in these cases it is more likely to find a path.
PP-based solutions are difficult to implement and customize. PP can be implemented with a very simple architecture. Setup can be difficult and time consuming, but the relative importance between the fields would be useful here (for example, which is more important to destroy the base or units?). Graphical representation of the PP is also very valuable.
Using Multi-agent Potential Fields in Real-time Strategy Games
Johan Hagelbäck and Stefan J. Johansson
International Conference on Autonomous Agents and Multi-agent Systems (AAMAS), 2008.
1. Download PDF
Real Time Strategy Bots
Johan Hagelbäck and Stefan J. Johansson.
Proceedings of Artificial Intelligence and Interactive Digital Entertainment (AIIDE), 2008.
2. Download PDF
A Multiagent Potential Field-Based Bot for Real-Time Strategy Games
Johan Hagelbäck and Stefan J. Johansson
International Journal of Computer Games Technology, 2009.
3. Download PDF
Learning Human-like Movement Behavior for Computer Games
C. Thurau, C. Bauckhage, and G. Sagerer
International Conference on the Simulation of Adaptive Behavior (SAB), 2004.
4. Download PDF
This lesson describes a game flow planning and unit navigation method that uses multi-agent potential fields. It is based on works under the numbers [1, 2, 3]. (See the end of the article links to the materials used)

')
What is a potential field?
PP (Potential Field) has a number of similarities with influence maps. Influence cards are often used to determine whether a zone in the game world is under the control of a player or enemies (in the range of weapons or movement), or is it a zone that is not currently controlled by anyone (nobody's land). The idea is to put positive values on the cells under the control of the player, and negative values - under the control of the enemy. Smoothly reducing the value to zero, we will create a map reflecting the influence of our own and enemy units in the zone. The figure below shows an example of an influence card with one of its own and one enemy unit.

Potential fields work in a similar way - a charge is put on the position of interest in the game world and generates a field that gradually drops to zero. The charge can be attractive (positive) or repulsive (negative). Please note that in some literature on potential fields negative charges attract and vice versa. In this lesson, positive charges are always repulsive. The figure below shows a simple game world with some impassable territory (brown), an enemy unit (green) and a destination of the unit (E). Attracting charge is located at the destination.

The charge generates a field that spreads across the game world:

And decays to zero:

Navigation with PP
In the illustration above, the attracting field spread around the destination point “E”. The idea is to allow the green unit to move to the positions with the most attracted values and eventually find the way to the destination point. To make it work, we also need to deal with the obstacles in the game world, in this case with the mountains (cinnamon zones). If we make the mountains generate small repulsive fields and combine them with attracting fields (from the picture above), we get a resultant field that can be used for navigation. Since units always move to the next position with the most attractive value, we will go around the mountains if there is another way.

The same idea is used for other obstacles. The picture below added two more of their units (white). They generate small repulsive fields, which are again added to the resulting field.

Thus, our green unit will bypass these units to avoid collisions. Now we have the final path for our unit. A unit can move from its current position to its destination and will bypass all obstacles without using any path finding algorithm.

Benefits of using PP
One of the most important advantages of using potential fields is the ability to handle dynamic game worlds. Since units (agents) move only one step at a time, instead of generating a full path from A to B, there is no risk that the path will become unavailable due to changes in the game world. Finding a path in a dynamic world can often be difficult to implement and require a large amount of resources to calculate. When an approach based on potential fields is used, the solution of the problem comes by itself, automatically. Of course, you need to be careful when implementing the software system to not forget to make updating potential fields as effective as possible. (More on this later).
Another important advantage is the ability to create complex behavior just by playing with the shape settings of the generated fields. Instead of linear attenuation to zero, we can use nonlinear fields. If we, for example, have shooting units like tanks in our army, we don’t want tanks to move too close to enemy units, but surround them at the right distance (for example, at a distance of their shooting range). This behavior can be achieved by placing a zero charge at the location of an enemy unit, generating an increasing field with the most attracted point at the firing range, and then decaying to zero. The picture below shows an example with two tanks (green) moving into an attack on an enemy unit (red), generating a non-linear PP.

An example of an equation for how such a field can be generated:

Here, W1 is the value for changing the relative field strength. D is the maximum firing range and R is the maximum detection range (whence our agent sees an enemy agent)
Another behavior that is easy to implement is “kicked-run”. First, the unit approaches the maximum attack distance.

After the attack, our unit must reload its weapon and retreats from the enemy unit until it is ready to fire again.

During the retreat phase, all enemy units generate a strong repulsive field with a radius of maximum firing range of the unit. This is an example of how specific potential fields can be active or inactive, depending on the internal state of the agent controlling this unit. An inactive field is simply ignored when the resulting potential field is summed.
The picture below is a screenshot of our bot, based on the PP for the ORTS engine. The left side of the image is a 2D view of the current state of the game. It shows our tanks (green circles), going to attack enemy bases (red squares) and units (red circles). Brown and black areas - impassable territory (mountains). The potential field of this game state is shown on the right side of the image. As in the other pictures from this lesson, the blue zones are the most attractive. The bright lines are the attacks of our tanks. The PP-view clearly shows how our units surround the enemy at the maximum distance of the shot, while at the same time avoiding collisions with each other and the terrain. The behavior of the enemy environment works perfectly and was probably one of the key ones in our success of the 2008th year at the ORTS tournament.

While we were developing our bot for ORTS, we found one thing - a completely different behavior, when the summation of the potentials of enemy units generated at each point was compared with just the highest potential of the enemy unit at that point. In the figure below, the potentials generated by the three enemy units are summed and added to the resulting field. Thus, the greatest potential is right in the center of the enemy unit cluster (circled in red), and our units are very eager to attack the enemies at their most powerful points.

The solution was not to summarize the potentials, but instead to take the greatest potential at a point from all units. In the latter case, the highest potential around enemies at an acceptable distance (shown by red lines).

Implementation notes
With a good plan and implementation of the PP system, the cost of resources for the calculation will not exceed the traditional solutions based on the algorithm A *. Our ORTS bot used the least amount of CPU resources in comparison with two other bots running on path finding algorithms from the 2007 tournament. However, we note that it is difficult to accurately calculate the use of the CPU, due to the fact that the winning bot uses more resources at the end of the game, as it has more units under control. Multithreading also complicates the task of calculating the required CPU resources. The comparison was made by comparing the total amount of CPU resources used by each client process in the Linux environment for 100 games. At the very least, we can conclude that the bot was good within the time frame of 0.125 seconds used in ORTS.
To improve performance, we divided the PP into three categories:
- Static fields. Fields that remain static the whole game. In our case, the terrain. This field is generated at startup.
- Semi-static field. Fields that do not require frequent updates. In our case, our and enemy bases. These fields are generated at startup and are updated when the database is destroyed.
- Dynamic fields. All the dynamic objects of the game world, such as our and enemy tanks. These fields are updated every frame. To reduce the calculation time, you can count them every second or third frame.
We experimented with two main architectures for generating PP ...
Pre-generation
The field generated by each type of object was calculated in advance and stored in static arrays in the header file. During the execution of the program, these fields were simply added to the general software in the desired position. To make this possible, the game world was divided into tiles, in our case each tile consisted of 8x8 points of the game world. This approach showed insufficient detailing and the bot performed poorly (2007 of the ORTS tournament). Since the game world was divided into significantly larger tiles, we were faced with the problems of deciding which tile (which tiles) an object is occupying. Suppose an object (an orange circle) and a base (an orange square). What tiles (gray squares) does our green unit occupy and what tiles should the base occupy?
This approach may be suitable for games like Wargus, which use a less detailed tile navigation system.


Real time calculations
Potentials generated at a point are calculated in real time by calculating the distance between the point and all the nearest objects, passing each distance as a variable to a function and then calculating the potential. This approach actually uses less CPU resources in our bot than pre-generated fields.
Thanks to:
- We consider the potentials of only those points that are candidates for the movement of units in them. In the pre-generated version, all potentials of the entire game world are considered (naturally, this can be optimized using a similar method).
- By calculating the distance to an object using the fast Manhattan method, we can avoid costly calculating the distance in Euclidean space for a large number of objects in the game world.
This approach was used in the second version of our bot (ORTS 2008 tournament). An example of the formula PP (with 2D and 3D graphs), used to calculate the potential generated by a cliff at a point with a distance "a" from the cliff.



And what about the local optimum problem?
One of the most common problems with PP is the problem of local optimum. In the picture below is an example when this problem appears. Destination "E" generates a circular field, which is blocked by the mountain. The unit moves to the positions with the highest potentials and ends at the largest where it currently stands. Unit stuck.

We solved this by using a trace similar to the pheromone trace described in [4]. Each agent controlling a unit adds a trace in the last N positions visited by the unit, as well as to the current position of the unit. The trail generates a light repulsive potential and “pushes” the unit forward. See how a track pushes a unit around a local optimum (yellow line) and the unit can find the way to the destination point.

But even with the traces there is a risk that the unit will get stuck in situations like the one in the picture below.

This can be solved by filling in the voids:

Conclusion
Below we have compiled criticism against decisions based on PP from our point of view:
The PP has problems like a local optimum that are difficult to solve. With the use of the trace, most local optima can be solved. The PP has problems in very difficult terrain; in these cases, methods of finding a path show themselves better. The power of PP in the processing of large dynamic worlds with large open spaces and the least difficult terrain. This is the case for many RTS games of today.
Solutions based on PP require a lot of resources. We have shown in our work that solutions based on software can be implemented with the same or even better efficiency as the methods of finding the path. Efficiency can be a problem, but in these cases it is more likely to find a path.
PP-based solutions are difficult to implement and customize. PP can be implemented with a very simple architecture. Setup can be difficult and time consuming, but the relative importance between the fields would be useful here (for example, which is more important to destroy the base or units?). Graphical representation of the PP is also very valuable.
Links
Using Multi-agent Potential Fields in Real-time Strategy Games
Johan Hagelbäck and Stefan J. Johansson
International Conference on Autonomous Agents and Multi-agent Systems (AAMAS), 2008.
1. Download PDF
Real Time Strategy Bots
Johan Hagelbäck and Stefan J. Johansson.
Proceedings of Artificial Intelligence and Interactive Digital Entertainment (AIIDE), 2008.
2. Download PDF
A Multiagent Potential Field-Based Bot for Real-Time Strategy Games
Johan Hagelbäck and Stefan J. Johansson
International Journal of Computer Games Technology, 2009.
3. Download PDF
Learning Human-like Movement Behavior for Computer Games
C. Thurau, C. Bauckhage, and G. Sagerer
International Conference on the Simulation of Adaptive Behavior (SAB), 2004.
4. Download PDF
Source: https://habr.com/ru/post/262181/
All Articles