Lines and probability theory

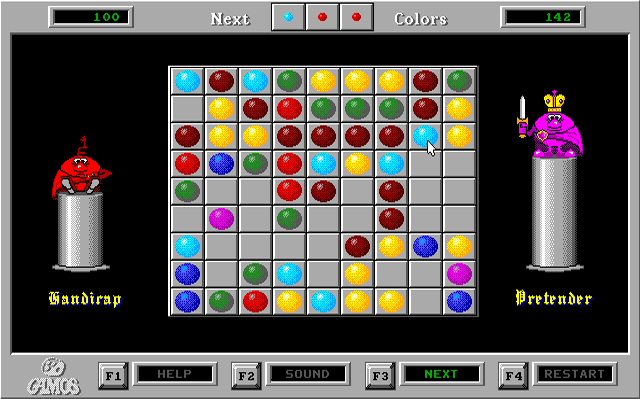
Everyone who played this game knows: if you now try to pull out the blue ball, which the cursor shows to put a burgundy in its place, then one of the coming three new balls will most likely “shut up” this place. If you try to pull it out again, it will shut up again. Throughout the long years of existence of this effect, my colleagues occasionally had disputes over whether it happened by chance or whether such a “trick” was made on purpose to make it harder to play.

Under the terms of the game, it is believed that the balls must fall into random fields. But for some reason, if there is a free field in the littered part of the board, it is filled first.
')
In this article, you will be able to go back 20 years ago and see how the reverse engineering process took place then. We will consider a 16-bit assembler code that chooses a place for the balls. There will not be modern 32-bit and 64-bit instructions, overgrown with special sets of commands, there will be no calls for dll, streams and other tricks. Only simple code. It seems to me that even those who have never seen an assembler will understand it. Those who wish can correct the algorithm so that it works “honestly”.

Let's start with the theory. The simplest obvious algorithm is: choose a random place on the board, and if it is occupied, repeat. And so on until we get to the free space. 20 years ago, I thought that this was the algorithm chosen by the author of the game and that is why the game is so “unfair”. I reasoned like this: what is the probability that in such a situation the next ball will fall into the only free field at the top of the board?



The probability of hitting the upper and lower halves is the same, but the lower one is almost free, and at the top there is only one free field. Therefore, if a random number falls into the bottom of the board, the algorithm will end immediately, and if it will drop to the top, it will repeat until it falls into that very single free field. That's why it turns out that such free fields “shut up” right away, and everything seems to be consistent with the actual behavior of the game.

But a person familiar with the theory of probability will immediately say that this is wrong. It's like a chance to meet a dinosaur on the street. Or meet, or not. The probability of a ball hitting any cell is the same, no matter how many and which cells are occupied. If in the last 10 moves a red ball never fell, then I understand that on the 11th move, most likely, it will still fall, although in fact the probability of falling out is now exactly the same as 10 moves back. If there is anyone else here who has not seen the " god Tetris ", be sure to take a look.

Is it really just an incredible set of circumstances or inaccuracies of a pseudo-random number generator? There is one assumption, but we will not run ahead. It's time to finally see how everything happens from the inside.

Take for example the English floppy version of the game, although you can take any other. To start you will need an emulator, such as dosbox . To study and fix the code, use Hiew. The author offers to download his old DOS version on his website for free.

Where to start? How to find the place in the program where a random number is selected? The board we have 9x9 cells. Let's try to look for 16-bit numbers 9 or 81. Nines are many, but 81 is just one. (81 = 51h)



That's just the 9s next to him, apparently we attacked the trail. Let's try to change 51 by 30 at random and see what happens. We start the game, and she immediately throws the entire field with balls and freezes. This is unexpected. Is this 81 irrelevant to the size of the field? Let's see what kind of cell [343E] where it was written to.



Well, just below the code the value of this cell is compared with "4C". Hmmm 76? What is this? I do not remember for how long this question put me at a dead end, but suddenly (like everything else in the process) it dawned on me: this is the number of free cells. At the very beginning of the game, 5 balls appear. At first the field is empty, there are 81 free cells. Then the balls are thrown out until this number becomes 76. So this is the section of the code where the initial initialization of the board is performed. One of the subroutines between these operations is to select the position for the ball. The “not-equal” transition, labeled as (8), forms a small cycle, in which there are only 2 calls. Let's see the first one.



After the standard operations with the stack, as we see, the number 50h (80) is taken, and is passed as an argument to call some procedure. The result, it obviously returns in the register AX, which is stored in the variable [bp] [- 2]. Then we take this number, divide it by 9 (div cx), increment it by 1 (inc ax), swap the quotient and the remainder, and store the quotient in the cell [39E4]. Then we do the same, only save the remainder of the same division in the cell [39E6].

Well, yes, it looks like it. A subroutine is probably a random number. At the exit, we have a random field number. Then we divide it by 9, we get two coordinates, X and Y. In a normal language, this could look like this:

cell = random(80); x = cell / 9 + 1; y = cell % 9 + 1; 

Go ahead:



Take the previously calculated X and Y. One of them is shifted to the left (shl) by 1 bit (multiplied by 2), memorized in CX. The other is multiplied by 12 (18), added to CX and used as an array index at [3490]. What could it be? Well, of course, the contents of the playing field, as a 2-dimensional array of 16-bit numbers. Therefore, X is multiplied by 2, and Y by 18. That is, we already have:

  cell = random(80); // .  0  79 x = cell / 9 + 1; y = cell % 9 + 1; if (field[x,y]!=0) ... 

And the next, last section that we need:



The contents of the cell are compared with zero. If so (apparently the cell is free?), Go ahead to 1E5A. If not, we increase the cell number (which we have a continuous numbering from 0 to 80). We compare it with 51 (81), if it is less - again we turn to 1E5A. If more - write there zero, that is, go to the top of the board. At this place, all the conditional branches we converge, and what are we doing? Repeats exactly the code from the previous picture to select the contents of the playing field and once again compared with zero. If it is not equal, then go back to the address 1E15, but this is not the very beginning, where a random number is selected, but the place where we calculate individual coordinates from it:

  cell = random(80); // .  0  79 next:x = cell / 9 + 1; y = cell % 9 + 1; if (field[x,y]!=0) { cell++; if(cell==81) cell=0; } if (field[x,y]!=0) goto next; 

Here is a get algorithm. We select a random cell, and then, if it is occupied, simply move across the field from left to right and from top to bottom and in a circle until we find an empty cell. That is the reason for the "dishonesty". Of course, with this algorithm, the probability of selecting cells will be very different, and will depend on the location of the balls already on the board.

Let us verify that this part of the code actually works in the game in the way we assume. Let's change at the beginning 50 to 28. Now, in theory, new balls should fall out only in the upper half of the board. We start, and nothing changes. Balls appear all over the board.

It turned out that the program has two almost identical subroutines, one of which throws out 5 balls of random color at the beginning of the game, and the other, 3 balls each during the game, but their colors are already known (because they must be shown in advance). Copy / paste rules! Well, we change this second subroutine, and make sure that it works.

Now, in order for the algorithm to “honestly” put the balls on random fields, it is enough to change the most recent transition a little higher, so that it goes on the repeated selection of a random number.


You can even check the result visually in the game. If you simply rearrange all the balls in the upper part of the board, then gradually it will become noticeable, as new balls fill first of all the free fields from top to bottom. This is especially noticeable when almost the entire board is full. After this modification, this effect disappears, and the balls begin to appear really in random places.

It remains to add that cell = random (81) should actually be, not 80. Because of this error, the balls never fall into the rightmost cell. Unless if all the cells to the left of it are occupied, then he will get there due to this “wrong” algorithm.

Oh, and one more thing. It would certainly be correct to choose a random number from 1 to the number of free cells, and put the ball right to the right place, knowing that it is free, and not to repeat the cycle until it gets to the right place. After all, if only one last cell remains, who knows how many times it will have to be repeated? How long will it take a 16-bit processor to perform so many cycles? And according to the theory of probability, it may happen that he never gets there at all. But we know that all these theories are nonsense, and sooner or later, and most likely after 80 cycles, the ball will definitely fall into this single cell.