Xonix to Javascript with pictures
Xonix is a popular DOS game, a Qix video game clone.
Xonix has already been ported to Javascript several times. The best and closest to the original of the existing implementations to date, perhaps, this one . At first I tried to adapt it for my implementation / modification ... But, unfortunately, the code even after deobfuscation did not become clear (at least for me). In addition, as far as I could understand, the code there is in places not entirely effective, or outdated. So I had to write everything from scratch.
As a result, I got such a "own" Xonix, with pictures and answers.
')
Demo | Sources
The code turned out to be quite voluminous, so here I will explain not everything, but only the most important (from my point of view) moments.
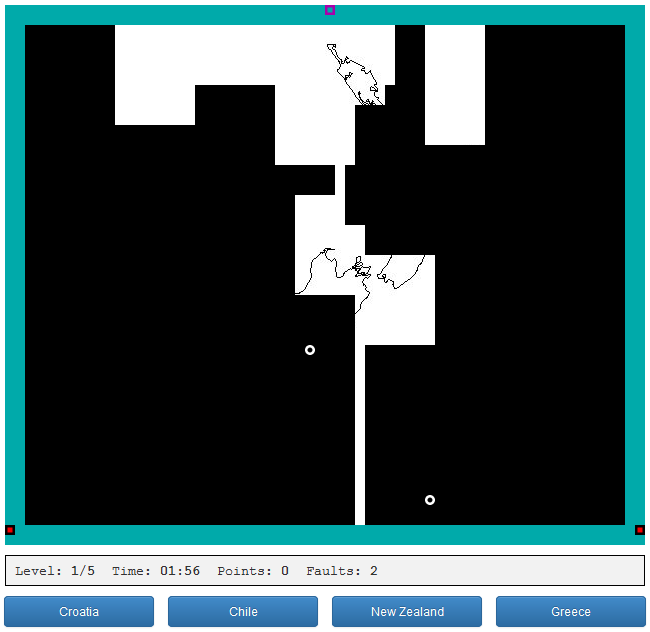
As you know, the playing field Xonix is ​​a grid of square cells. At the beginning of the game (level) most of the field is occupied by a rectangular black area ("sea"), which is surrounded by a light frame ("land") on all sides.
The main difference between my implementation and the classic Xonix is ​​that behind the black area there is a picture that is unique for each level. By this, she is like another modification of Xonix - Sexonix. But in my picture does not appear just like that. This is part of the question to be answered. And the whole game thus turns into a quiz.
The size of the image determines the size of the black area, which must be a multiple of the cell size. In the general case, the pictures for different levels of the game can have different sizes, therefore the dimensions of the black area can vary from level to level, in contrast to the light frame, which at the beginning of the level always has a fixed width of 2 cells.
The movement of all objects ( cursor and points ) occurs strictly in the cells, so that at each moment in time each object occupies exactly one cell. This structure of the playing field greatly simplifies the implementation of the game. The difficulty is only the definition of "conquered" areas, formed when the cursor crosses the "sea", but more on that later.
The fact that we can take a cell as a “pixel” eliminates most of the computational problems that are commonly found in games with many moving objects: motion calculations, bounces and collisions, etc.
In Xonix, any object has only 4 directions of movement: for the cursor - up / down / left / right, for a point (of both types) - the same, only diagonally. We combine these options into many possible directions, which will be given in degrees. We get 8 angles of motion: from 0 to 315 degrees in increments of 45. To each angle value, we assign a pair of motion direction vector coordinates. The result is a structure that we will use when calculating the motion:
The
Collisions of points with each other can be ignored, just let them “pass” through each other. Since all points (of the same type) look the same, from the outside it will be no different from collision and rebound.
To calculate collisions of points with a cursor, rebound of points from the border of "their" area and some other things, we need a matrix of states of all cells - a two-dimensional array
where
Each element will store the state of the corresponding cell, which includes 2 signs: the type of area to which it belongs (sea / land), as well as whether there is a “trace” on it at the moment from the cursor movement over the “sea”. This state will be stored in a two-bit bit field . To do this, we need to declare two mask constants for each attribute, respectively:
In order to optimize, we will make the array of states not two-dimensional, but one-dimensional, so that all elements will be stored line by line, starting with the first (top) line. To convert cell coordinates into an array index and inverse transform we will use the following formulas:
To calculate the rebound point ("sea" or "land") from the border of "our" area, we need to know the state of the three cells, not counting the cell of the point itself. Below, using pseudographics, the position of these cells relative to the current cell of the point is shown at a 45 degree angle of motion.
The cell of a point is marked with a cross, and the desired cells are numbered 1, 2, 3. Zeroes just represent neighboring cells. The direction of motion of the point in this case is southeast, since the ordinate axis (Y) of the grid is directed downwards.
A rebound from the border occurs if at least one of the three cells indicated has the type of area opposite to the type of point. Those. if, for example, the "sea" point, then one of these cells must be "land". At the same time, if this condition is satisfied only in one of the cells 1 or 2 (but not in both), then the angle of motion is added, respectively,
At any other angle of motion, the logic of the rebound will obviously be exactly the same.
Collision of a point with a cursor leads to pausing the game, after which the cursor and the “land” points return to their original starting positions for the game: the cursor - to the middle cell in the second row, the “land” points depending on their number - in the bottom and side parts of the frame . The position of the "sea" points does not change.
The definition of a collision of a “land” point with a cursor is trivial. Just check the contact point with the cursor, comparing the coordinates of the point and cursor cells. Determining the collision of the “sea” point with the cursor is a bit more difficult: we need to check not only the contact of the point itself with the cursor, but also the touch of the track of the cursor movement. To do this, use the second bit of the state of the cells: we check it on all the cells adjacent to the point.
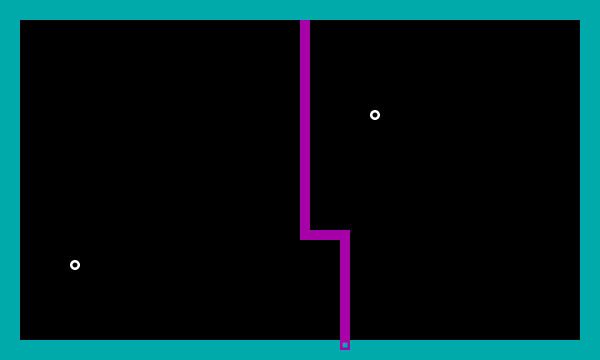
As already mentioned, the most difficult thing to implement is the definition of areas “conquered” from the “sea”. These are the closed areas formed as a result of the intersection of the “sea” cursor, within which there are no “sea” points. In most cases, two closed areas are formed, which are obtained by dividing (following the cursor movement) the available “sea” area into two parts, of which only one or “none” becomes “conquered” (see screenshot 1). But in some, especially difficult cases, a multitude of closed (see screenshot 2), including “conquered” areas, can be formed at once. In addition, it is possible that the trace of the cursor itself forms a closed area (see screenshot 3).
Screenshot 1
Screenshot 2
Screenshot 3
So, we need to find all such closed areas, and then determine the type of each of them ("conquered" / "undefeated").
To find closed areas, you can iterate through all the cells using some general algorithm for comparing neighboring cells. For example, as implemented here .
But there is another way (which I ultimately chose): to use the contours of closed areas formed when the cursor is crossing the "sea". The contour refers to a closed polyline with a thickness of one cell. If the contour of the closed area is known, then it remains only to find its contents, i.e. all the cells inside it. But how to find these contours?
In the general case, we only know about each desired contour that it has a partial intersection with the trace of the cursor movement, i.e. contains at least one cell trace cursor. In most cases, as shown in screenshot 1, exactly two contours are formed, each of which contains the entire trace of the entire cursor (all its cells). But in some cases, as in screenshot 2, there may be many such contours, and many of them may contain only a portion of the cursor trace cells. In addition, it is necessary to consider the cases when the entire trace of the cursor itself forms a closed loop (screenshot 3). Thus, it is necessary, on the basis of the data about the trace of the cursor, to obtain all the information about the contours of the closed regions adjoining it, while checking as few cells as possible.
Considering the various options for the distribution of contours, you can find several patterns. First, the number of contours containing the entire trace of the entire cursor is always no more than 2. Secondly, if all the contours are divided into 2 groups on opposite sides of the cursor trace, the contours of one group will not have common trace cells. In other words, each cell of the cursor trace belongs to only one contour on each side of the track.
Based on the above, it is possible to derive an algorithm for finding contours. In general terms, it looks like this.
We loop through all the cells that belong to the trace of the cursor, starting with the first one (that is, from the beginning of the movement). For each cell of the track, we check two adjacent cells on both sides of it (to the left and to the right in the direction of motion). If the cell is “marine”, then this is part of the contour of one of the areas sought. Otherwise, we continue searching until we find a “marine” cell on this side of the track. From the found cell, you can extend the entire circuit adjacent to it. To do this, go from this cell first in the direction from the trace cell, and then in such a direction that at least on one side of the current cell there is always a “land” cell (in this case, the current cell must be “marine”). And so on until a trace cell is encountered, which means that the contour is closed. Add to the passed cells a part of the trace cells needed to close the broken line, and we get the desired contour.
After this, we continue the external cycle of iterating the cells of the trace, starting with the one on which the procedure for finding the contour from one cell stopped above.
It should be noted that the procedures for finding the contours on both sides of the track should be performed independently of each other. This means that the loop for iterating over the cells of a trace needs to be wrapped into one more cycle of 2 iterations — one for each side.
It is possible that no circuit will be found from either side. This means that the trail of movement is adjacent to the border of the "marine" area. In this case, we will have a unique closed domain consisting only of the trace itself.
If there is a situation from screenshot 3, all contours found must be added to the contour formed by the whole trace of the cursor.
Now that the outlines of the closed areas have been found, it is necessary to determine the content of the corresponding area (all cells contained in it) and its type (“conquered” or not) for each contour. Since the cursor can only move vertically / horizontally in Xonix, each closed area can be divided into several rectangles of different sizes. Thus, the task of determining the contents of a closed area is reduced to finding the rectangles that constitute it. By the way, by this we “kill” at once two “birds with one stone”: we make it easier to count the points inside the closed areas, as well as to paint over (or rather erase) the “conquered” areas.
To find the rectangles, it is enough to know the vertices of the contour of the region, i.e. vertices of a polygon.
The basic idea is to cut off a protruding rectangle with the greatest width or height from each area at each iteration. A speaker here is a rectangle whose three vertices belong to the original polygon. Based on this, we can derive an algorithm for partitioning a closed area into rectangles. It looks like this.
At the first iteration we find the side (segment) of the polygon with the greatest length, which is part of the protruding rectangle. If there are several such segments, choose any of them. The found segment will be one of the sides of the required rectangle. Now we need to find the rest of his hand. To do this, take the segments emanating from both ends of the found side perpendicular to it, and choose the shortest one. This will be the second side of the rectangle. To find the third side, you need to find the (orthogonal) projection of the second end of this segment onto the second of the segments that are perpendicular to the first side. Connect the found point with the corresponding end of the first side and get the third side. From here we get the entire desired outlined rectangle. Now we need to cut it off from the original polygon. To do this, remove the first and second found segments and the corresponding vertices from the polygon, then add the found projection point, connecting it with the vertex that was previously connected to the second found segment. As a result, we obtain a polygon having two vertices smaller than the original one.
At the next iteration, we will work with a trimmed polygon according to the same scheme as in the first iteration ... And so on until we get a polygon from 4 vertices as a result, ie rectangle.
All the rectangles cut off in the considered process will make up the contents of the closed area.
Consider the process of splitting into rectangles on a specific example.
Suppose we have a polygon
1. Find the side of the polygon
2. Find the side of the
3. Find the side of the
4. Find the side of the
As a result, we get 5 rectangles that make up the contents of a closed area:
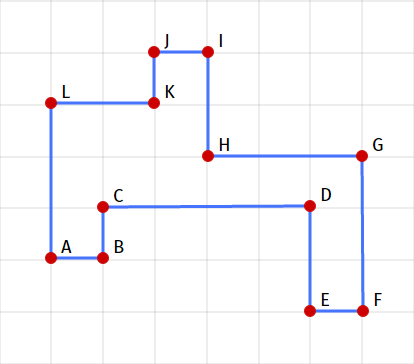Fig. one
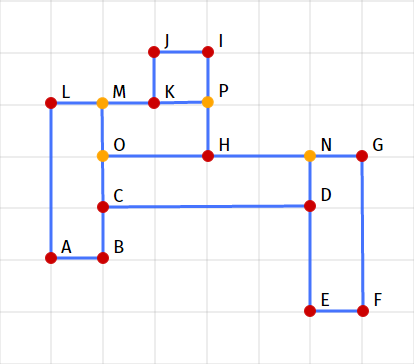Fig. 2
After the closed areas are found, it is necessary to determine the type of each of them (whether it is “conquered” or not). The type of area is determined by counting the "sea" points inside it. It is not necessary to count all the points inside the region, it is enough just to find out if at least one point is there. If there is, then this area is not “conquered” (and, accordingly, we do not erase it), because there should not be a single point in the “conquered” area.
Determining whether a polygon of arbitrary shape contains a point with a given position (coordinates) is, in general, very difficult. But we also divided the polygon into rectangles in order to facilitate this task as well. Unlike an arbitrary polygon, determining whether a point belongs to a rectangle is a trivial task. You just need to check the belonging of each coordinate of this point to the corresponding range of borders of the rectangle.
Thus, the task of determining the type of a closed area is reduced to the search for "sea" points inside each of the rectangles that make up this area.
All found "conquered" areas are subject to erasure, which is implemented even more trivially: simply erase (using the clearRect method) all the rectangles that make up this area.
The title is a bit deceiving). The article has already come to an end, so, unfortunately, none of the above will be there. I can only note that I wrote the animation code on the basis of this article ( translation ), as well as this ( translation ).
For those who are interested, below is the entire code of the game. However, its value is questionable, because comments there - the cat cried. But I hope I explained the main logic.
For this round. Thanks for attention.
Xonix has already been ported to Javascript several times. The best and closest to the original of the existing implementations to date, perhaps, this one . At first I tried to adapt it for my implementation / modification ... But, unfortunately, the code even after deobfuscation did not become clear (at least for me). In addition, as far as I could understand, the code there is in places not entirely effective, or outdated. So I had to write everything from scratch.
As a result, I got such a "own" Xonix, with pictures and answers.
')
Demo | Sources
The code turned out to be quite voluminous, so here I will explain not everything, but only the most important (from my point of view) moments.
As you know, the playing field Xonix is ​​a grid of square cells. At the beginning of the game (level) most of the field is occupied by a rectangular black area ("sea"), which is surrounded by a light frame ("land") on all sides.
The main difference between my implementation and the classic Xonix is ​​that behind the black area there is a picture that is unique for each level. By this, she is like another modification of Xonix - Sexonix. But in my picture does not appear just like that. This is part of the question to be answered. And the whole game thus turns into a quiz.
The size of the image determines the size of the black area, which must be a multiple of the cell size. In the general case, the pictures for different levels of the game can have different sizes, therefore the dimensions of the black area can vary from level to level, in contrast to the light frame, which at the beginning of the level always has a fixed width of 2 cells.
The movement of all objects ( cursor and points ) occurs strictly in the cells, so that at each moment in time each object occupies exactly one cell. This structure of the playing field greatly simplifies the implementation of the game. The difficulty is only the definition of "conquered" areas, formed when the cursor crosses the "sea", but more on that later.
The movement of objects
The fact that we can take a cell as a “pixel” eliminates most of the computational problems that are commonly found in games with many moving objects: motion calculations, bounces and collisions, etc.
In Xonix, any object has only 4 directions of movement: for the cursor - up / down / left / right, for a point (of both types) - the same, only diagonally. We combine these options into many possible directions, which will be given in degrees. We get 8 angles of motion: from 0 to 315 degrees in increments of 45. To each angle value, we assign a pair of motion direction vector coordinates. The result is a structure that we will use when calculating the motion:
Code snippet
dirset = { vecs: { 0: [1, 0], 45: [1, 1], 90: [0, 1], 135: [-1, 1], 180: [-1, 0], 225: [-1, -1], 270: [0, -1], 315: [1, -1] }, get: function(v) { return v in this.vecs? this.vecs[v] : [0, 0]; }, find: function(x, y) { x = x == 0? 0 : (x > 0? 1 : -1); y = y == 0? 0 : (y > 0? 1 : -1); for (var v in this.vecs) { var vec = this.vecs[v]; if (vec[0] == x && vec[1] == y) return parseInt(v); } return false; } }; The
get method returns the corresponding motion vector for a given angle (in degrees). The find method does the opposite: for a given motion vector (not necessarily a single), it returns the corresponding angle in degrees, or the closest available angle to it.Collisions of points with each other can be ignored, just let them “pass” through each other. Since all points (of the same type) look the same, from the outside it will be no different from collision and rebound.
To calculate collisions of points with a cursor, rebound of points from the border of "their" area and some other things, we need a matrix of states of all cells - a two-dimensional array
(n+4) * (m+4) ,where
(n+4) , (m+4) is the width and height of the playing field in the cells, respectively, and the first element of the matrix corresponds to the cell in the upper left corner of the playing field.Each element will store the state of the corresponding cell, which includes 2 signs: the type of area to which it belongs (sea / land), as well as whether there is a “trace” on it at the moment from the cursor movement over the “sea”. This state will be stored in a two-bit bit field . To do this, we need to declare two mask constants for each attribute, respectively:
var CA_CLEAR = 1 << 0; // , .. var CA_TRAIL = 1 << 1; // - "" In order to optimize, we will make the array of states not two-dimensional, but one-dimensional, so that all elements will be stored line by line, starting with the first (top) line. To convert cell coordinates into an array index and inverse transform we will use the following formulas:
i = n * (y + 2) + x + 2; x = i % n - 2; y = Math.floor(i / n) - 2 To calculate the rebound point ("sea" or "land") from the border of "our" area, we need to know the state of the three cells, not counting the cell of the point itself. Below, using pseudographics, the position of these cells relative to the current cell of the point is shown at a 45 degree angle of motion.
OOO OX1 O23
The cell of a point is marked with a cross, and the desired cells are numbered 1, 2, 3. Zeroes just represent neighboring cells. The direction of motion of the point in this case is southeast, since the ordinate axis (Y) of the grid is directed downwards.
A rebound from the border occurs if at least one of the three cells indicated has the type of area opposite to the type of point. Those. if, for example, the "sea" point, then one of these cells must be "land". At the same time, if this condition is satisfied only in one of the cells 1 or 2 (but not in both), then the angle of motion is added, respectively,
+90 or -90 degrees. Otherwise, the angle of movement is reversed ( +180 degrees).At any other angle of motion, the logic of the rebound will obviously be exactly the same.
Collision of a point with a cursor leads to pausing the game, after which the cursor and the “land” points return to their original starting positions for the game: the cursor - to the middle cell in the second row, the “land” points depending on their number - in the bottom and side parts of the frame . The position of the "sea" points does not change.
The definition of a collision of a “land” point with a cursor is trivial. Just check the contact point with the cursor, comparing the coordinates of the point and cursor cells. Determining the collision of the “sea” point with the cursor is a bit more difficult: we need to check not only the contact of the point itself with the cursor, but also the touch of the track of the cursor movement. To do this, use the second bit of the state of the cells: we check it on all the cells adjacent to the point.
Definition of "conquered" areas
As already mentioned, the most difficult thing to implement is the definition of areas “conquered” from the “sea”. These are the closed areas formed as a result of the intersection of the “sea” cursor, within which there are no “sea” points. In most cases, two closed areas are formed, which are obtained by dividing (following the cursor movement) the available “sea” area into two parts, of which only one or “none” becomes “conquered” (see screenshot 1). But in some, especially difficult cases, a multitude of closed (see screenshot 2), including “conquered” areas, can be formed at once. In addition, it is possible that the trace of the cursor itself forms a closed area (see screenshot 3).
So, we need to find all such closed areas, and then determine the type of each of them ("conquered" / "undefeated").
To find closed areas, you can iterate through all the cells using some general algorithm for comparing neighboring cells. For example, as implemented here .
But there is another way (which I ultimately chose): to use the contours of closed areas formed when the cursor is crossing the "sea". The contour refers to a closed polyline with a thickness of one cell. If the contour of the closed area is known, then it remains only to find its contents, i.e. all the cells inside it. But how to find these contours?
Outlines of closed areas
In the general case, we only know about each desired contour that it has a partial intersection with the trace of the cursor movement, i.e. contains at least one cell trace cursor. In most cases, as shown in screenshot 1, exactly two contours are formed, each of which contains the entire trace of the entire cursor (all its cells). But in some cases, as in screenshot 2, there may be many such contours, and many of them may contain only a portion of the cursor trace cells. In addition, it is necessary to consider the cases when the entire trace of the cursor itself forms a closed loop (screenshot 3). Thus, it is necessary, on the basis of the data about the trace of the cursor, to obtain all the information about the contours of the closed regions adjoining it, while checking as few cells as possible.
Considering the various options for the distribution of contours, you can find several patterns. First, the number of contours containing the entire trace of the entire cursor is always no more than 2. Secondly, if all the contours are divided into 2 groups on opposite sides of the cursor trace, the contours of one group will not have common trace cells. In other words, each cell of the cursor trace belongs to only one contour on each side of the track.
Based on the above, it is possible to derive an algorithm for finding contours. In general terms, it looks like this.
We loop through all the cells that belong to the trace of the cursor, starting with the first one (that is, from the beginning of the movement). For each cell of the track, we check two adjacent cells on both sides of it (to the left and to the right in the direction of motion). If the cell is “marine”, then this is part of the contour of one of the areas sought. Otherwise, we continue searching until we find a “marine” cell on this side of the track. From the found cell, you can extend the entire circuit adjacent to it. To do this, go from this cell first in the direction from the trace cell, and then in such a direction that at least on one side of the current cell there is always a “land” cell (in this case, the current cell must be “marine”). And so on until a trace cell is encountered, which means that the contour is closed. Add to the passed cells a part of the trace cells needed to close the broken line, and we get the desired contour.
After this, we continue the external cycle of iterating the cells of the trace, starting with the one on which the procedure for finding the contour from one cell stopped above.
It should be noted that the procedures for finding the contours on both sides of the track should be performed independently of each other. This means that the loop for iterating over the cells of a trace needs to be wrapped into one more cycle of 2 iterations — one for each side.
It is possible that no circuit will be found from either side. This means that the trail of movement is adjacent to the border of the "marine" area. In this case, we will have a unique closed domain consisting only of the trace itself.
If there is a situation from screenshot 3, all contours found must be added to the contour formed by the whole trace of the cursor.
Content and type of closed area
Now that the outlines of the closed areas have been found, it is necessary to determine the content of the corresponding area (all cells contained in it) and its type (“conquered” or not) for each contour. Since the cursor can only move vertically / horizontally in Xonix, each closed area can be divided into several rectangles of different sizes. Thus, the task of determining the contents of a closed area is reduced to finding the rectangles that constitute it. By the way, by this we “kill” at once two “birds with one stone”: we make it easier to count the points inside the closed areas, as well as to paint over (or rather erase) the “conquered” areas.
To find the rectangles, it is enough to know the vertices of the contour of the region, i.e. vertices of a polygon.
The basic idea is to cut off a protruding rectangle with the greatest width or height from each area at each iteration. A speaker here is a rectangle whose three vertices belong to the original polygon. Based on this, we can derive an algorithm for partitioning a closed area into rectangles. It looks like this.
At the first iteration we find the side (segment) of the polygon with the greatest length, which is part of the protruding rectangle. If there are several such segments, choose any of them. The found segment will be one of the sides of the required rectangle. Now we need to find the rest of his hand. To do this, take the segments emanating from both ends of the found side perpendicular to it, and choose the shortest one. This will be the second side of the rectangle. To find the third side, you need to find the (orthogonal) projection of the second end of this segment onto the second of the segments that are perpendicular to the first side. Connect the found point with the corresponding end of the first side and get the third side. From here we get the entire desired outlined rectangle. Now we need to cut it off from the original polygon. To do this, remove the first and second found segments and the corresponding vertices from the polygon, then add the found projection point, connecting it with the vertex that was previously connected to the second found segment. As a result, we obtain a polygon having two vertices smaller than the original one.
At the next iteration, we will work with a trimmed polygon according to the same scheme as in the first iteration ... And so on until we get a polygon from 4 vertices as a result, ie rectangle.
All the rectangles cut off in the considered process will make up the contents of the closed area.
Consider the process of splitting into rectangles on a specific example.
Suppose we have a polygon
ABCDEFGHIJKL (see Fig. 1), which is the contour of a region. We apply the stepwise described partitioning algorithm.1. Find the side of the polygon
ABCDEFGHIJKL with the greatest length. This is a piece of CD with a length of 4. But it does not suit us, because not part of the protruding rectangle. Therefore, ignore it and look for further. Find 3 segments with a length of 3: AL , FG , GH . GH doesn't suit us for the same reason as CD . So there are segments AL , FG . Choose any of them. Let it be AL . The segments perpendicular to it are AB and KL , of which the shortest is AB . Find the projection of point B on the segment KL - this is point M (see fig. 2). Thus we obtain a clip rectangle - ABML . After it is cut off, the polygon CDEFGHIJKM remains.2. Find the side of the
CDEFGHIJKM polygon with the longest length. This is a FG segment with a length of 3 ... The intersecting rectangle is FGNE (see Fig. 2). After it is cut off, the polygon CDNHIJKM remains.3. Find the side of the
CDNHIJKM polygon with the longest length. This is already familiar to us segment of CD with a length of 4 ... Cut-off rectangle - CDNO . After it is cut off, the OHIJKM polygon OHIJKM .4. Find the side of the
OHIJKM polygon with the greatest length. There are two such sides. These are the OH and HI segments with a length of 2. Choose the first of them, OH ... The cut-off rectangle is OHPM . After it is cut off, the KPIJ rectangle KPIJ . Now there is nothing to cut off. So the algorithm ends here.As a result, we get 5 rectangles that make up the contents of a closed area:
ABML , FGNE , CDNO , OHPM and KPIJ (see Fig. 2).After the closed areas are found, it is necessary to determine the type of each of them (whether it is “conquered” or not). The type of area is determined by counting the "sea" points inside it. It is not necessary to count all the points inside the region, it is enough just to find out if at least one point is there. If there is, then this area is not “conquered” (and, accordingly, we do not erase it), because there should not be a single point in the “conquered” area.
Determining whether a polygon of arbitrary shape contains a point with a given position (coordinates) is, in general, very difficult. But we also divided the polygon into rectangles in order to facilitate this task as well. Unlike an arbitrary polygon, determining whether a point belongs to a rectangle is a trivial task. You just need to check the belonging of each coordinate of this point to the corresponding range of borders of the rectangle.
Thus, the task of determining the type of a closed area is reduced to the search for "sea" points inside each of the rectangles that make up this area.
All found "conquered" areas are subject to erasure, which is implemented even more trivially: simply erase (using the clearRect method) all the rectangles that make up this area.
Animation, game management and more
The title is a bit deceiving). The article has already come to an end, so, unfortunately, none of the above will be there. I can only note that I wrote the animation code on the basis of this article ( translation ), as well as this ( translation ).
For those who are interested, below is the entire code of the game. However, its value is questionable, because comments there - the cat cried. But I hope I explained the main logic.
Game code
// requestAnimationFrame/cancelAnimationFrame polyfill: (function() { var tLast = 0; var vendors = ['webkit', 'moz']; for(var i = 0; i < vendors.length && !window.requestAnimationFrame; ++i) { var v = vendors[i]; window.requestAnimationFrame = window[v+'RequestAnimationFrame']; window.cancelAnimationFrame = window[v+'CancelAnimationFrame'] || window[v+'CancelRequestAnimationFrame']; } if (!window.requestAnimationFrame) window.requestAnimationFrame = function(callback, element) { var tNow = Date.now(); var dt = Math.max(0, 17 - tNow + tLast); var id = setTimeout(function() { callback(tNow + dt); }, dt); tLast = tNow + dt; return id; }; if (!window.cancelAnimationFrame) window.cancelAnimationFrame = function(id) { clearTimeout(id); }; }()); (function() { window.picxonix = function(v1, v2) { if (typeof v1 != 'string') { return init(v1, v2); } switch (v1) { case 'level': // loadLevel(v2); break; case 'end': // endLevel(v2); break; case 'play': // / setPlayMode(v2); break; case 'cursorDir': // typeof v2 == 'string'? setDir(v2) : setDirToward(v2); break; case 'cursorSpeed': // setCursorSpeed(v2); break; case 'enemySpeed': // setEnemySpeed(v2); break; case 'enemySpawn': // spawn(); break; case 'state': // return buildLevelState(); default: } return 0; } var cfgMain = { width: 600, height: 400, sizeCell: 10, colorFill: '#000000', colorBorder: '#00aaaa', colorBall: '#ffffff', colorBallIn: '#000000', colorWarder: '#000000', colorWarderIn: '#f80000', colorCursor: '#aa00aa', colorCursorIn: '#00aaaa', colorTrail: '#a800a8', timeoutCollision: 1000, callback: null, callbackOnFrame: false }; var cfgLevel = { nBalls: 1, nWarders: 1, speedCursor: 5, speedEnemy: 5 }; // cell attributes: var CA_CLEAR = 1 << 0; var CA_TRAIL = 1 << 1; // : var sizeCell; var width, height; // : var elContainer; var ctxPic; var ctxMain; var imgPic; var imgBall; var imgWarder; var imgCursor; // : var dirset; var cellset; var cursor; var aBalls = [], aWarders = []; var nBalls = 0, nWarders = 0; // : var idFrame = 0; var tLevel = 0; var tLastFrame = 0; var tLocked = 0; var bCollision = false; var bConquer = false; var dirhash = { 'left': 180, 'right': 0, 'up': 270, 'down': 90, 'stop': false }; function init(el, opts) { if (elContainer || !el || !el.appendChild) return false; elContainer = el; // : merge(cfgMain, opts); if (!cfgMain.sizeCell) return false; sizeCell = cfgMain.sizeCell; if (typeof cfgMain.callback != 'function') cfgMain.callback = null; // : if (opts.speedCursor ^ opts.speedEnemy) { opts.speedCursor = opts.speedEnemy = Math.max(opts.speedCursor || 0, opts.speedEnemy || 0); } merge(cfgLevel, opts); setLevelData(cfgMain.width, cfgMain.height); var oWrap = document.createElement('div'); oWrap.style.position = 'relative'; // (): (function() { var canvas = document.createElement('canvas'); ctxPic = canvas.getContext('2d'); canvas.width = width; canvas.height = height; canvas.style.position = 'absolute'; canvas.style.left = canvas.style.top = (2*sizeCell) + 'px'; ctxPic.fillStyle = cfgMain.colorTrail; ctxPic.fillRect(0, 0, width, height); oWrap.appendChild(canvas); }()); // : (function() { var canvas = document.createElement('canvas'); ctxMain = canvas.getContext('2d'); canvas.width = width+ 4*sizeCell; canvas.height = height+ 4*sizeCell; canvas.style.position = 'absolute'; canvas.style.left = canvas.style.top = 0; fillCanvas(); ctxMain.fillStyle = cfgMain.colorFill; ctxMain.fillRect(2*sizeCell, 2*sizeCell, width, height); oWrap.appendChild(canvas); }()); elContainer.appendChild(oWrap); // : var canvas = document.createElement('canvas'); var ctxTmp = canvas.getContext('2d'); canvas.width = sizeCell; canvas.height = sizeCell; // : var r = sizeCell / 2, q = sizeCell / 4; ctxTmp.clearRect(0, 0, sizeCell, sizeCell); ctxTmp.beginPath(); ctxTmp.arc(r, r, r, 0, Math.PI * 2, false); ctxTmp.fillStyle = cfgMain.colorBall; ctxTmp.fill(); if (cfgMain.colorBallIn) { ctxTmp.beginPath(); ctxTmp.arc(r, r, q, 0, Math.PI * 2, false); ctxTmp.fillStyle = cfgMain.colorBallIn; ctxTmp.fill(); } imgBall = new Image(); imgBall.src = ctxTmp.canvas.toDataURL(); function prepareSquare(colorOut, colorIn) { ctxTmp.clearRect(0, 0, sizeCell, sizeCell); ctxTmp.fillStyle = colorOut; ctxTmp.fillRect(0, 0, sizeCell, sizeCell); if (colorIn) { ctxTmp.fillStyle = colorIn; ctxTmp.fillRect(q, q, sizeCell - r, sizeCell - r); } } // : prepareSquare(cfgMain.colorWarder, cfgMain.colorWarderIn); imgWarder = new Image(); imgWarder.src = ctxTmp.canvas.toDataURL(); // : prepareSquare(cfgMain.colorCursor, cfgMain.colorCursorIn); imgCursor = new Image(); imgCursor.src = ctxTmp.canvas.toDataURL(); return {width: width+ 4*sizeCell, height: height+ 4*sizeCell}; } function loadLevel(data) { if (tLevel || tLastFrame || !data || !data.image) return; if (!data.image) return; var img = new Image(); img.onload = function() { applyLevel(img, data); }; img.src = data.image; } function applyLevel(img, data) { imgPic = img; merge(cfgLevel, data, true); setLevelData(img.width, img.height); ctxMain.canvas.width = width+ 4*sizeCell; ctxMain.canvas.height = height+ 4*sizeCell; fillCanvas(); cellset.reset(); ctxPic.canvas.width = width; ctxPic.canvas.height = height; ctxPic.drawImage(imgPic, 0, 0, width, height, 0, 0, width, height); var pos = cellset.placeCursor(); cursor.reset(pos[0], pos[1]); aBalls = []; aWarders = []; var i, aPos; aPos = cellset.placeBalls(nBalls); for (i = 0; i < nBalls; i++) aBalls.push(new Enemy(aPos[i][0], aPos[i][1], false)); aPos = cellset.placeWarders(nWarders); for (i = 0; i < nWarders; i++) aWarders.push(new Enemy(aPos[i][0], aPos[i][1], true, 45)); tLevel = Date.now(); tLastFrame = 0; startLoop(); } function endLevel(bClear) { if (tLastFrame) return; tLevel = 0; if (!bClear) return; fillCanvas(); ctxMain.clearRect(2*sizeCell, 2*sizeCell, width, height); } function setLevelData(w, h) { if (w) width = w - w % (2*sizeCell); if (h) height = h - h % (2*sizeCell); if (cfgLevel.nBalls) nBalls = cfgLevel.nBalls; if (cfgLevel.nWarders) nWarders = cfgLevel.nWarders; } function setPlayMode(bOn) { if (bOn ^ !tLastFrame) return; tLastFrame? endLoop() : startLoop(); } function setDir(key) { if (!tLastFrame) return; if (key in dirhash) cursor.setDir(dirhash[key]); } function setDirToward(pos) { if (!tLastFrame || !pos || pos.length < 2) return; var xc = Math.floor(pos[0] / sizeCell) - 2, yc = Math.floor(pos[1] / sizeCell) - 2; var b = cellset.isPosValid(xc, yc); if (!b) return; var posCr = cursor.pos(), dirCr = cursor.getDir(), dir = false; if (dirCr === false) { var dx = xc - posCr[0], dy = yc - posCr[1], dc = Math.abs(dx) - Math.abs(dy); if (dc == 0) return; dir = dirset.find(dx, dy); if (dir % 90 != 0) { var dir1 = dir-45, dir2 = dir+45; dir = dir1 % 180 == 0 ^ dc < 0? dir1 : dir2; } } else { var delta = dirCr % 180? xc - posCr[0] : yc - posCr[1]; if (!delta) return; dir = (delta > 0? 0 : 180) + (dirCr % 180? 0 : 90); } cursor.setDir(dir); } function setCursorSpeed(v) { if (v > 0) cfgLevel.speedCursor = v; } function setEnemySpeed(v) { if (v > 0) cfgLevel.speedEnemy = v; } function startLoop() { if (!tLevel) return; idFrame = requestAnimationFrame(loop); } function endLoop() { if (idFrame) cancelAnimationFrame(idFrame); tLastFrame = idFrame = 0; } // function loop(now) { var dt = tLastFrame? (now - tLastFrame) / 1000 : 0; bCollision = bConquer = false; if (!tLastFrame || update(dt)) { render(); tLastFrame = now; } if (bCollision) { lock(); cfgMain.callback && cfgMain.callback(1); return; } if (bConquer) { bConquer = false; tLastFrame = 0; cellset.conquer(); if (cfgMain.callback && cfgMain.callback(2)) return; } else cfgMain.callback && cfgMain.callbackOnFrame && cfgMain.callback(0); startLoop(); } function update(dt) { var distCursor = Math.round(dt * cfgLevel.speedCursor), distEnemy = Math.round(dt * cfgLevel.speedEnemy); if (!(distCursor >= 1 || distEnemy >= 1)) return false; cursor.update(distCursor); var i; for (i = 0; i < nBalls; i++) aBalls[i].update(distEnemy); for (i = 0; i < nWarders; i++) aWarders[i].update(distEnemy); return true; } function render() { cellset.render(); cursor.render(); var i; for (i = 0; i < nBalls; i++) aBalls[i].render(); for (i = 0; i < nWarders; i++) aWarders[i].render(); } function lock() { tLastFrame = 0; bCollision = false; var posCr = cursor.pos(); cellset.add2Trail(posCr[0], posCr[1], false); setTimeout(unlock, cfgMain.timeoutCollision); } function unlock() { if (!tLevel) return; cellset.clearTrail(); var pos = cellset.placeCursor(); cursor.reset(pos[0], pos[1], true); var aPos = cellset.placeWarders(nWarders); for (var i = 0; i < nWarders; i++) aWarders[i].reset(aPos[i][0], aPos[i][1]); startLoop(); } function spawn() { if (!tLevel) return; var pos = cellset.placeSpawned(); if (!pos) return; aWarders.push(new Enemy(pos[0], pos[1], true)); nWarders++; } function buildLevelState() { return { play: Boolean(tLastFrame), posCursor: cursor.pos(), warders: nWarders, speedCursor: cfgLevel.speedCursor, speedEnemy: cfgLevel.speedEnemy, cleared: cellset.getPercentage() }; } function fillCanvas() { ctxMain.fillStyle = cfgMain.colorBorder; ctxMain.fillRect(0, 0, width+ 4*sizeCell, height+ 4*sizeCell); } function drawCellImg(img, x, y) { ctxMain.drawImage(img, 0, 0, sizeCell, sizeCell, (x+2)*sizeCell, (y+2)*sizeCell, sizeCell, sizeCell ); } function clearCellArea(x, y, w, h) { ctxMain.clearRect( (x+2)*sizeCell, (y+2)*sizeCell, (w || 1)* sizeCell, (h || 1)* sizeCell ); } function fillCellArea(color, x, y, w, h) { ctxMain.fillStyle = color; ctxMain.fillRect( (x+2)*sizeCell, (y+2)*sizeCell, (w || 1)* sizeCell, (h || 1)* sizeCell ); } // : dirset = { vecs: { 0: [1, 0], 45: [1, 1], 90: [0, 1], 135: [-1, 1], 180: [-1, 0], 225: [-1, -1], 270: [0, -1], 315: [1, -1] }, get: function(v) { return v in this.vecs? this.vecs[v] : [0, 0]; }, find: function(x, y) { x = x == 0? 0 : (x > 0? 1 : -1); y = y == 0? 0 : (y > 0? 1 : -1); for (var v in this.vecs) { var vec = this.vecs[v]; if (vec[0] == x && vec[1] == y) return parseInt(v); } return false; } }; // : cellset = { nW: 0, nH: 0, nWx: 0, nCleared: 0, dirTrail: 0, iPreTrail: 0, aCells: [], aTrail: [], aTrailNodes: [], aTrailRects: [], reset: function() { var nW = this.nW = Math.floor(width / sizeCell); var nH = this.nH = Math.floor(height / sizeCell); var n = (this.nWx = nW+4)* (nH+4); this.nCleared = 0; this.aCells = []; var aAll = []; for (var i = 0; i < n; i++) { var pos = this.pos(i), x = pos[0], y = pos[1]; this.aCells.push(x >= 0 && x < nW && y >= 0 && y < nH? 0 : CA_CLEAR); aAll.push(i); } fillCellArea(cfgMain.colorFill, 0, 0, nW, nH); }, render: function() { if (this.aTrailRects.length) { for (var i = this.aTrailRects.length-1; i >= 0; i--) { fillCellArea.apply(null, [cfgMain.colorFill].concat(this.aTrailRects[i])); } this.aTrailRects = []; } }, isPosIn: function(x, y) { return x >= 0 && x < this.nW && y >= 0 && y < this.nH; }, isPosValid: function(x, y) { return x >= -2 && x < this.nW+2 && y >= -2 && y < this.nH+2; }, find: function(x, y) { return this.isPosValid(x, y) ? (this.nWx)*(y+2) + x+2 : -1; }, pos: function(i) { return [i % this.nWx - 2, Math.floor(i / this.nWx)-2]; }, posMap: function(arr) { var _this = this; return arr.map(function(v) { return _this.pos(v) }); }, value: function(x, y) { var i = this.find(x,y); return i >= 0? this.aCells[i] : 0; }, set: function(x, y, v) { var i = this.find(x,y); if (i >= 0) this.aCells[i] = v; return i; }, setOn: function(x, y, v) { var i = this.find(x,y); if (i >= 0) this.aCells[i] |= v; return i; }, setOff: function(x, y, v) { var i = this.find(x,y); if (i >= 0) this.aCells[i] &= ~v; return i; }, placeCursor: function() { return [Math.floor(this.nW/2), -2]; }, placeBalls: function(n) { var a = [], ret = []; for (var i = 0; i < n; i++) { var k; do k = Math.floor(Math.random() * this.nW * this.nH); while (a.indexOf(k) >= 0); a.push(k); var x = k % this.nW, y = Math.floor(k / this.nW); ret.push([x, y]); } return ret; }, placeWarders: function(n) { var z; var aPos = [ [Math.floor(this.nW/2), this.nH+1], [-1, this.nH+1], [this.nW, this.nH+1], [-1, -2], [this.nW, -2], [-1, z = Math.floor(this.nH/2)], [this.nW, z], [z = Math.floor(this.nW/4), this.nH+1], [3*z, this.nH+1] ]; var i0 = (n+ 1)% 2; return aPos.slice(i0, Math.min(n+ i0, 9)); }, placeSpawned: function() { if (nWarders >= 9) return false; function dist(pos1, pos2) { return Math.pow(pos1[0]- pos2[0], 2) + Math.pow(pos1[1]- pos2[1], 2); } function find(pos0) { var n = nWarders; for (var l = 0; l < x0; l++) { for (var dx = -1; dx <= 1; dx+= 2) { var p = [pos0[0]+ l* dx, pos0[1]]; for (var i = 0; i < n && dist(aWarders[i].pos(), p) >= 4; i++) ; if (i >= n) return p; } } return pos0; } var x0 = Math.floor(this.nW/2); var aPos = [[x0, this.nH+1], [x0, -2]]; var posCr = cursor.pos(); var posSt = dist(aPos[0], posCr) > dist(aPos[1], posCr)? aPos[0] : aPos[1]; var ret = find(posSt); return ret; }, applyRelDirs: function(x, y, dir, aDeltas) { var ret = []; for (var n = aDeltas.length, i = 0; i < n; i++) { var d = (dir + aDeltas[i] + 360) % 360; var vec = dirset.get(d), xt, yt; ret.push([xt = x + vec[0], yt = y + vec[1], d, this.value(xt, yt)]); } return ret; }, add2Trail: function(x, y, dir) { var i = this.setOn(x, y, CA_TRAIL); if (i < 0) return; var n = this.aTrail.length; if (!n || dir !== this.dirTrail) { var iNode = n? this.aTrail[n-1] : i; if (!n || iNode != this.aTrailNodes[this.aTrailNodes.length-1]) this.aTrailNodes.push(iNode); if (!n) { var aPos = this.applyRelDirs(x, y, dir, [180]); this.iPreTrail = this.find(aPos[0][0], aPos[0][1]); } } this.aTrail.push(i); this.dirTrail = dir; }, lastTrailLine: function() { var pos0 = this.pos(this.aTrailNodes[this.aTrailNodes.length-1]), pos = this.pos(this.aTrail[this.aTrail.length-1]); return [ Math.min(pos[0], pos0[0]), Math.min(pos[1], pos0[1]), Math.abs(pos[0] - pos0[0])+1, Math.abs(pos[1] - pos0[1])+1 ]; }, clearTrail: function() { this.aTrailRects = this._buildTrailRects(); for (var n = this.aTrail.length, i = 0; i < n; i++) { this.aCells[this.aTrail[i]] &= ~CA_TRAIL; } this.aTrail = []; this.aTrailNodes = []; }, getPreTrail: function() { return this.iPreTrail; }, conquer: function() { var nTrail = this.aTrail.length; if (!nTrail) return; if (nTrail > 1) this.aTrailNodes.push(this.aTrail[nTrail-1]); var aConqRects = this._conquer() || this._buildTrailRects(); this.aTrail = []; this.aTrailNodes = []; if (!aConqRects || !aConqRects.length) return; for (var n = aConqRects.length, i = 0; i < n; i++) { var rect = aConqRects[i]; var x0 = rect[0], y0 = rect[1], w = rect[2], h = rect[3]; for (var x = 0; x < w; x++) { for (var y = 0; y < h; y++) { if (this.value(x + x0, y + y0, CA_CLEAR) & CA_CLEAR) continue; this.set(x + x0, y + y0, CA_CLEAR); this.nCleared++; } } } for (i = 0; i < n; i++) { clearCellArea.apply(null, aConqRects[i]); } aConqRects = []; }, getPercentage: function() { return this.nCleared / (this.nW * this.nH) * 100; }, _conquer: function() { var nTrail = this.aTrail.length, nNodes = this.aTrailNodes.length; var dz = Math.abs(this.aTrailNodes[0] - this.aTrailNodes[nNodes-1]); var aOutlineset = [], bClosedTrail = false; if (bClosedTrail = nNodes >= 4 && dz == 1 || dz == this.nWx) { aOutlineset.push([this.aTrailNodes, 1]); } var bAddTrail = false; var posPre = this.pos(this.iPreTrail), posCr = cursor.pos(); var aDeltas = [-90, 90]; for (var d = 0; d < 2; d++) { var dd = aDeltas[d]; var k = 0; var sum = 0, bSum = false, bEndAtNode = false; for (var l = 0; l < nTrail && sum < nTrail; l++) { var iStart = this.aTrail[l]; var pos = this.pos(iStart); var pos0 = l? this.pos(this.aTrail[l - 1]) : posPre; var x = pos[0], y = pos[1]; var dir = (dirset.find(x - pos0[0], y - pos0[1]) + dd + 360) % 360; var aDirs = bEndAtNode? [] : [dir]; if (this.aTrailNodes.indexOf(iStart) >= 0) { var pos2 = l < nTrail - 1? this.pos(this.aTrail[l + 1]) : posCr; dir = (dirset.find(pos2[0] - x, pos2[1] - y) + dd + 360) % 360; if (dir != aDirs[0]) aDirs.push(dir); } if (this.aTrail[l] == this.aTrailNodes[k+1]) ++k; var ret = 0; for (var nDs = aDirs.length, j = 0; j < nDs && !ret; j++) { dir = aDirs[j]; var vec = dirset.get(dir); var xt = x + vec[0], yt = y + vec[1]; var v = this.value(xt, yt); if (v & CA_CLEAR || v & CA_TRAIL) continue; ret = this._outline(xt, yt, dir); if (!ret || ret.length < 3) return false; } bEndAtNode = false; if (!ret) continue; var len = ret[0], aNodes = ret[1], bClosed = ret[2], iEnd = aNodes[aNodes.length-1]; if (bClosed) { aOutlineset.push([aNodes, len]); bSum = true; continue; } var aXtra = [iStart]; for (var i = l+1; i < nTrail && this.aTrail[i] != iEnd; i++) { if (this.aTrail[i] == this.aTrailNodes[k+1]) aXtra.push(this.aTrailNodes[++k]); } if (i >= nTrail) continue; aOutlineset.push([aNodes.concat(aXtra.reverse()), len + i - l]); sum += i - l + 1; l = (bEndAtNode = this.aTrail[i] == this.aTrailNodes[k+1])? i-1 : i; } if (!sum && !bSum && !bClosedTrail) return false; if (sum < nTrail && !bClosedTrail) bAddTrail = true; } if (!aOutlineset.length) return false; aOutlineset.sort(function (el1, el2) { return el1[1] - el2[1]; }); var aRects = [], n = aOutlineset.length, b = false; for (i = 0; i < n; i++) { if (i == n- 1 && !b) break; ret = this._buildConquerRects(aOutlineset[i][0]); if (ret) aRects = aRects.concat(ret); else b = true; } if (!aRects.length) return false; return bAddTrail? aRects.concat(this._buildTrailRects()) : aRects; }, _outline: function(x0, y0, dir) { var aNodes = [], aUniqNodes = [], aUsedDirs = [], aBackDirs = []; var x = x0, y = y0, lim = 6 * (this.nW + this.nH), n = 0, bClosed = false; function isClear(arr) { return arr[3] & CA_CLEAR; } do { bClosed = n && x == x0 && y == y0; var iCurr = this.find(x,y), iUniq = aUniqNodes.indexOf(iCurr); var aCurrUsed = iUniq >= 0? aUsedDirs[iUniq] : []; var aCurrBack = iUniq >= 0? aBackDirs[iUniq] : []; var aPosOpts = this.applyRelDirs(x,y, dir, [-90, 90, 0]); var aTestDirs = [180+45, -45, 45, 180-45, -45, 45]; var aPassIdx = [], aPassWeight = []; for (var i = 0; i < 3; i++) { var d = aPosOpts[i][2]; if (aCurrUsed.indexOf(d) >= 0) continue; if (isClear(aPosOpts[i])) continue; var aTestOpts = this.applyRelDirs(x,y, dir, aTestDirs.slice(i*2,i*2+2)); var b1 = isClear(aTestOpts[0]), b2 = isClear(aTestOpts[1]); var b = b1 || b2 || (i == 2? isClear(aPosOpts[0]) || isClear(aPosOpts[1]) : isClear(aPosOpts[2])); if (!b) continue; aPassIdx.push(i); aPassWeight.push( (b1 && b2? 0 : b1 || b2? 1 : 2) + (aCurrBack.indexOf(d) >= 0? 3 : 0) ); } var nPass = aPassIdx.length; var min = false, idx = false; for (i = 0; i < nPass; i++) { if (!i || aPassWeight[i] < min) { min = aPassWeight[i]; idx = aPassIdx[i]; } } var pos = nPass? aPosOpts[idx] : this.applyRelDirs(x,y, dir, [180])[0]; var dir0 = dir; x = pos[0]; y = pos[1]; dir = pos[2]; if (pos[2] == dir0) continue; nPass? aNodes.push(iCurr) : aNodes.push(iCurr, iCurr); dir0 = (dir0 + 180) % 360; if (iUniq < 0) { aUniqNodes.push(iCurr); aUsedDirs.push([dir]); aBackDirs.push([dir0]); } else { aUsedDirs[iUniq].push(dir); aBackDirs[iUniq].push(dir0); } } while (n++ < lim && !(this.value(x, y) & CA_TRAIL)); if (!(n < lim)) return false; if (bClosed) { aNodes.push(iCurr); if (aNodes[0] != (iCurr = this.find(x0,y0))) aNodes.unshift(iCurr); var nNodes = aNodes.length; if (nNodes % 2 && aNodes[0] == aNodes[nNodes-1]) aNodes.pop(); } else aNodes.push(this.find(x,y)); return [n+1, aNodes, bClosed]; }, _buildTrailRects: function() { if (this.aTrailNodes.length == 1) this.aTrailNodes.push(this.aTrailNodes[0]); var aRects = []; for (var n = this.aTrailNodes.length, i = 0; i < n-1; i++) { var pos1 = this.pos(this.aTrailNodes[i]), pos2 = this.pos(this.aTrailNodes[i+1]); var x0 = Math.min(pos1[0], pos2[0]), y0 = Math.min(pos1[1], pos2[1]); var w = Math.max(pos1[0], pos2[0]) - x0 + 1, h = Math.max(pos1[1], pos2[1]) - y0 + 1; var rect = [x0, y0, w, h]; aRects.push(rect); } return aRects; }, _buildConquerRects: function(aOutline) { if (aOutline.length < 4) return false; var aNodes = this.posMap(aOutline); var n = aNodes.length; if (n > 4 && n % 2 != 0) { var b1 = aNodes[0][0] == aNodes[n-1][0], b2; if (b1 ^ aNodes[0][1] == aNodes[n-1][1]) { b2 = aNodes[n-2][0] == aNodes[n-1][0]; if (!(b2 ^ b1) && b2 ^ aNodes[n-2][1] == aNodes[n-1][1]) aNodes.pop(); b2 = aNodes[0][0] == aNodes[1][0]; if (!(b2 ^ b1) && b2 ^ aNodes[0][1] == aNodes[1][1]) aNodes.shift(); } b1 = aNodes[0][0] == aNodes[1][0]; b2 = aNodes[1][0] == aNodes[2][0]; if (!(b1 ^ b2) && b1 ^ aNodes[0][1] == aNodes[1][1] && b2 ^ aNodes[1][1] == aNodes[2][1]) aNodes.shift(); } if (aNodes.length % 2 != 0) return false; var aRects = []; for (var l = 0; l < 10 && aNodes.length > 4; l++) { n = aNodes.length; var dim1 = 0, dim2 = 0, iBase = 0, iCo = 0; var posB1, posB2, posT1, posT2; for (var i = 0; i < n; i++) { posB1 = aNodes[i]; posB2 = aNodes[(i+1)%n]; posT1 = aNodes[(i-1+n)%n]; posT2 = aNodes[(i+2)%n]; var dir = dirset.find(posT1[0]-posB1[0], posT1[1]-posB1[1]); if (dir != dirset.find(posT2[0]-posB2[0], posT2[1]-posB2[1])) continue; var dirTest = Math.floor((dirset.find(posB2[0]-posB1[0], posB2[1]-posB1[1])+ dir) / 2); var vec = dirset.get(dirTest - dirTest% 45); if (this.value([posB1[0]+ vec[0], posB1[1]+ vec[1]]) & CA_CLEAR) continue; var b = false, t, w, k; if ((t = Math.abs(posB1[0]-posB2[0])) > dim1) { b = true; k = 0; w = t; } if ((t = Math.abs(posB1[1]-posB2[1])) > dim1) { b = true; k = 1; w = t; } if (!b) continue; var k2 = (k+1)%2; vec = dirset.get(dir); var sgn = vec[k2]; var co2 = posB1[k2]; var left = Math.min(posB1[k], posB2[k]), right = Math.max(posB1[k], posB2[k]); var min = Math.min(sgn* (posT1[k2]- co2), sgn* (posT2[k2]- co2)); for (var j = i% 2; j < n; j+= 2) { if (j == i) continue; var pos = aNodes[j], pos2 = aNodes[(j+1)%n], h; if (pos[k2] == pos2[k2] && (h = sgn*(pos[k2]- co2)) >= 0 && h < min && pos[k] > left && pos[k] < right && pos2[k] > left && pos2[k] < right) break; } if (j < n) continue; dim1 = w; dim2 = sgn*min; iBase = i; iCo = k; } var iB2 = (iBase+1)%n, iT1 = (iBase-1+n)%n, iT2 = (iBase+2)%n; posB1 = aNodes[iBase]; posB2 = aNodes[iB2]; posT1 = aNodes[iT1]; posT2 = aNodes[iT2]; var aDim = [0, 0], pos0 = []; var iCo2 = (iCo+1)%2; aDim[iCo] = dim1; aDim[iCo2] = dim2; pos0[iCo] = Math.min(posB1[iCo], posB2[iCo]); pos0[iCo2] = Math.min(posB1[iCo2], posB2[iCo2]) + (aDim[iCo2] < 0? aDim[iCo2]: 0); var rect = [pos0[0], pos0[1], Math.abs(aDim[0])+1, Math.abs(aDim[1])+1]; var bC = Math.abs(posT1[iCo2] - posB1[iCo2]) == Math.abs(dim2); if (this._containBall(rect)) return false; aRects.push(rect); if (bC) { posB2[iCo2] += dim2; aNodes.splice(iBase,1); aNodes.splice(iT1 < iBase? iT1 : iT1-1, 1); } else { posB1[iCo2] += dim2; aNodes.splice(iT2,1); aNodes.splice(iB2 < iT2? iB2 : iB2-1, 1); } } var aX = aNodes.map(function(v) {return v[0]}); var aY = aNodes.map(function(v) {return v[1]}); var x0 = Math.min.apply(null, aX); var y0 = Math.min.apply(null, aY); rect = [x0, y0, Math.max.apply(null, aX)-x0+1, Math.max.apply(null, aY)-y0+1]; if (this._containBall(rect)) return false; aRects.push(rect); return aRects; }, // , . : _containBall: function(rect) { var x1 = rect[0], x2 = x1+ rect[2] - 1; var y1 = rect[1], y2 = y1+ rect[3] - 1; for (var i = 0; i < nBalls; i++) { var o = aBalls[i], x = ox, y = oy; if (x >= x1 && x <= x2 && y >= y1 && y <= y2) return true; } return false; } }; // : cursor = { x: 0, // x y: 0, // y x0: 0, // x y0: 0, // y dir: false, // ( ) state: false, // (true - ) state0: false, // // : reset: function(x, y, bUnlock) { var bPre = bUnlock && cellset.value(this.x, this.y) & CA_CLEAR; this.x0 = bPre? this.x : x; this.y0 = bPre? this.y : y; this.x = x; this.y = y; this.dir = this.state = this.state0 = false; }, // - : update: function(dist) { if (this.dir === false) return; var x = this.x, y = this.y; var vec = dirset.get(this.dir), vecX = vec[0], vecY = vec[1]; var bEnd = false; for (var n = 0; n < dist; n++) { if (cellset.find(x + vecX, y + vecY) < 0) { this.dir = false; break; } x += vecX; y += vecY; if (cellset.value(x, y) & CA_TRAIL) { bCollision = true; break; } var b = cellset.value(x, y) & CA_CLEAR; if (this.state && b) { bEnd = true; break; } this.state = !b; if (this.state) cellset.add2Trail(x, y, this.dir); } this.x = x; this.y = y; if (!bEnd) return; if (cellset.getPreTrail() == cellset.find(x,y)) bCollision = true; else { this.dir = this.state = false; bConquer = true; } }, // : render: function() { if (this.x0 == this.x && this.y0 == this.y) { if (tLastFrame) return; } else { if (this.state0) { var rect = cellset.lastTrailLine(); fillCellArea.apply(null, [cfgMain.colorTrail].concat(rect)); } else { if (cellset.isPosIn(this.x0, this.y0)) clearCellArea(this.x0, this.y0); else fillCellArea(cfgMain.colorBorder, this.x0, this.y0); } this.x0 = this.x; this.y0 = this.y; } this.state0 = this.state; drawCellImg(imgCursor, this.x, this.y); }, // : pos: function() { return [this.x, this.y]; }, // : getDir: function() { return this.dir; }, // : setDir: function(dir) { if (dir === this.dir) return; if (this.state && this.dir !== false && Math.abs(dir - this.dir) == 180) return; this.dir = dir; } }; // ( ): function Enemy(x, y, type, dir) { this.x = x; this.y = y; this.x0 = x; this.y0 = y; var aDirs = [45, 135, 225, 315]; this.dir = dir === undefined? aDirs[Math.floor(Math.random()*4)] : dir; // this.type = Boolean(type); // (boolean) (false - , true - ) } // : Enemy.prototype = { // : reset: function(x, y) { this.x = x; this.y = y; }, // - : update: function(dist) { var ret = this._calcPath(this.x, this.y, dist, this.dir); this.x = ret.x; this.y = ret.y; this.dir = ret.dir; }, // : render: function() { if (this.x0 == this.x && this.y0 == this.y) { if (tLastFrame) return; } else { if (this.type && cellset.isPosIn(this.x0, this.y0)) clearCellArea(this.x0, this.y0); else fillCellArea(this.type? cfgMain.colorBorder : cfgMain.colorFill, this.x0, this.y0); this.x0 = this.x; this.y0 = this.y; } drawCellImg(this.type? imgWarder : imgBall, this.x, this.y); }, // : pos: function() { return [this.x, this.y]; }, // (): _calcPath: function(x, y, dist, dir) { var vec = dirset.get(dir), vecX = vec[0], vecY = vec[1]; var posCr = cursor.pos(); var xC = posCr[0], yC = posCr[1], vC = cellset.value(xC, yC), bC = !this.type ^ vC & CA_CLEAR; if (bC && Math.abs(x - xC) <= 1 && Math.abs(y - yC) <= 1 || !this.type && this._isCollision(x, y, dir)) { bCollision = true; } for (var n = 0; n < dist && !bCollision; n++) { var xt = x + vecX, yt = y + vecY; var dirB = this._calcBounce(x, y, dir, xt, yt); if (dirB !== false) return this._calcPath(x, y, dist - n, dirB); if (bC && Math.abs(xt - xC) <= 1 && Math.abs(yt - yC) <= 1 || !this.type && this._isCollision(xt, yt, dir)) bCollision = true; if (!this.type && !cellset.isPosIn(xt, yt)) break; x = xt; y = yt; } return {x: x, y: y, dir: dir}; }, // ( ): _calcBounce: function(x, y, dir, xt, yt) { var ret = cellset.applyRelDirs(x,y, dir, [-45, 45]); var b1 = this.type ^ ret[0][3] & CA_CLEAR, b2 = this.type ^ ret[1][3] & CA_CLEAR; return b1 ^ b2? (b1? dir + 90 : dir + 270) % 360 : this.type ^ cellset.value(xt, yt) & CA_CLEAR || b1 && b2? (dir+180) % 360 : false; }, // : _isCollision: function(x, y, dir) { if (cellset.value(x, y) & CA_TRAIL) return true; var aDirs = [-45, 45, -90, 90]; for (var i = 0; i < 4; i++) { var d = (dir + aDirs[i] + 360) % 360, vec = dirset.get(d); if (cellset.value(x + vec[0], y + vec[1]) & CA_TRAIL) return true; } return false; } }; function merge(dest, src, bFilter) { if (!src) return dest; for(var key in dest) { if (!dest.hasOwnProperty(key) || !src.hasOwnProperty(key)) continue; var v = src[key]; if ((!bFilter || v) && (typeof v != 'number' || v >= 0)) dest[key] = v; } return dest; } })(); For this round. Thanks for attention.
Source: https://habr.com/ru/post/261853/
All Articles