The formula for calculating the number of days in the month
Note : This post is a translation of the article cmcenroe.me/2014/12/05/days-in-month-formula.html ( Part I ), as well as the author's supplement to it ( Part II ). You should not take the material seriously, but rather as a warm-up for the mind, requiring nothing more than school knowledge of arithmetic and no practical application. Enjoy everyone!
Recently, after another sleepless night, I thought about the methods of memorizing the number of days in each month of the year. To do this, there is a count, as well as a way to count on the knuckles, but neither did suit me. I wondered if there was any mathematical formula for solving such a problem, and - not finding one with a quick study - I challenged myself to create it.
Formalizing In other words, it is necessary to find a function f , such that the value of f (x) for each month x , represented by a number from 1 to 12, is equal to the number of days in that month. The table of argument values and functions 1 :
If you have a desire to try yourself before reading my decision, now is the time. If you prefer to see the ready answer immediately, then look under the spoiler.
Below are my steps to find a solution.
First, let's briefly refresh two vital operators in solving this task: integer division and remainder of division.
')
Integer division is an operator used in many programming languages when dividing two integers and discarding the fractional part of the private part. I will depict him as . For example:
. For example:

The remainder of the division is the operator that finds the remainder of the division. In many programming languages, the % symbol is used, but I will use constructions of the form , eg:
, eg:
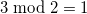
I note that the remainder of the division has the same priority as division.
So, let's apply our mathematical apparatus to obtain the basic formula. 2 In the usual month of 30 or 31 days, so that we can use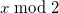 to get alternately 1 or 0, and then just add a constant to this number:
to get alternately 1 or 0, and then just add a constant to this number:
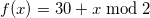
We get the table, the correct values are highlighted in bold:
Not a bad start! There are already correct values for January and for the months from March to July inclusive. February is a special case, and we'll figure it out a little later. After July, for the remaining months, the order of receiving 0 and 1 should be reversed.
To do this, we can add to the dividend 1:
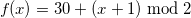
Now the correct values are from August to December, but, as expected, the values for the other months are incorrect. Let's see how we can combine these formulas.
For this, a piecewise-defined function is necessary, but - since it seemed boring to me - I thought about a different solution using one part of the function on one interval, the other on the other.
I believe that the easiest way is to find an expression equal to 1 in one application and 0 in the rest. The method in which multiplying the argument by the expression we exclude it from the formula outside its scope, I called the “mask overlay”, because this behavior is similar to a bit mask.
To use this method in the last part of our function, you need to find an expression equal to 1 for , and - since the argument values are always less than 16 - the integer division by 8 is perfect for this.
, and - since the argument values are always less than 16 - the integer division by 8 is perfect for this.
Now using this mask using in delimited expression
expression  instead of 1, we can replace the order of getting 0 and 1 formula with the reverse:
instead of 1, we can replace the order of getting 0 and 1 formula with the reverse:
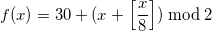
Eureka! Everything is correct, except February. Surprise surprise.
In any month 30 or 31 days, except February with its 28th (leap year is beyond the scope of this task). 3 At the moment, according to our formula, it has 30 days, so it would be nice to subtract an expression equal to 2 when .
.
The best I managed to think of that puts a mask on all months after February:
that puts a mask on all months after February:
Changing the base constant to 28 with the addition of 2 to the remaining months, we obtain the formula:

Unfortunately, January is now shorter by 2 days. But, fortunately, to get an expression that will only be used for the first month is very easy: it’s a rounded down reverse to number. Multiplying it by 2 yields the final formula:
number. Multiplying it by 2 yields the final formula:

Here it is - a formula for obtaining the number of days in any month of the year, using simple arithmetic. The next time you remember how many days in September, just follow using this single line javascript function:
using this single line javascript function:
In the first part, a short and even slightly elegant formula was obtained, the main advantages of which are the simplicity of the mathematical apparatus, the absence of branching and conditional expressions, conciseness. The disadvantages - besides the fact that you will not apply it in your project - can be attributed to the absence of a check for a leap year and a non-leap year.
Therefore, I set myself the task to create a function f , such that the value of f (x, y) for each month x , represented by a number from 1 to 12 and the year y greater than 0, equals the number of days in month x in the year y .
For the impatient under the spoiler is a ready answer, the rest, please follow me.
For visual clarity, we agree that in some formulas the division operator with the remainder is replaced by bottom brackets, where it seemed necessary to me:

An additional calendar day is introduced in a leap year: February 29. As you know, a leap year is a multiple of 4 and not a multiple of 100, or a multiple of 400. We write the expression identical with this statement:

To bring this expression into algebraic, you must apply to the result of the expression injection form:
injection form:

That will allow you to get 1 when dividing without remainder and 0 when dividing with remainder, to use it in the formula for determining the number of days in a month.
As a function of g ', you can use 1 minus the remainder of the division for
for 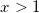 :
:
It is easy to see that increasing the dividend and the divisor by 1, we get the correct formula at
at  :
:
Thus the expression write as:
write as:

And the expression write as:
write as:

Applying this approach, we obtain the following function g (y) , the value of which will be 1 if the year is a leap year, or 0 in the opposite case:

Leap years are highlighted in bold.
I remind you that within the framework of the accepted agreement, the operator for obtaining the remainder of division can be depicted as mod and ⌊⌋.
In the formula part
part  is an amendment, adding 2 days to January. If we remove the factor 2 and replace the numerator with 1 by 2, then this formula will add 2 days to January and 1 day to February, which gives us the key to adding a day in a leap year. For clarity, we use the intermediate value of g (y) in the formula and use 2000 (leap) and 2001 (not leap) years as y :
is an amendment, adding 2 days to January. If we remove the factor 2 and replace the numerator with 1 by 2, then this formula will add 2 days to January and 1 day to February, which gives us the key to adding a day in a leap year. For clarity, we use the intermediate value of g (y) in the formula and use 2000 (leap) and 2001 (not leap) years as y :

Values for all months except January are not leap years are correct.
To correct this unfortunate misunderstanding, add to January 1 day already known to us by the formula :
:

Now you need to subtract 1 day from January in the case of a leap year, for which we will be helped by the knowledge that for any x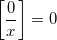 , but
, but  .
.
Then the formula will look like:


Or:

As a result, a much more cumbersome, but more universal formula has been obtained, which can also be used to obtain the number of days in a month of a particular year:
An example in C # ideone.com/fANutz .
1 . I do not know how to use this mnemonic, so I spied on the tablet on the Internet.
2 "Basics," or "Rule With Many Exceptions," like most rules.
3 Initially, in the Roman calendar, February was the last month of the year, so there is a logic that it is shorter than all the others. There is also a logic to add or delete a day at the end of the year, so its length is variable.
Upd. one:
An alternative translation of the first part in the community VKontakte .
Upd. 2: Thanks to the keksmen commentary, the error in the leap year definition formula ( g (y) ) was corrected and the final formula was corrected.
Part I
Introduction
Recently, after another sleepless night, I thought about the methods of memorizing the number of days in each month of the year. To do this, there is a count, as well as a way to count on the knuckles, but neither did suit me. I wondered if there was any mathematical formula for solving such a problem, and - not finding one with a quick study - I challenged myself to create it.
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x) | 31 | 28 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
If you have a desire to try yourself before reading my decision, now is the time. If you prefer to see the ready answer immediately, then look under the spoiler.
Answer

Below are my steps to find a solution.
Mathematical apparatus
First, let's briefly refresh two vital operators in solving this task: integer division and remainder of division.
')
Integer division is an operator used in many programming languages when dividing two integers and discarding the fractional part of the private part. I will depict him as
 . For example:
. For example:
The remainder of the division is the operator that finds the remainder of the division. In many programming languages, the % symbol is used, but I will use constructions of the form
 , eg:
, eg: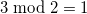
I note that the remainder of the division has the same priority as division.
The basics
So, let's apply our mathematical apparatus to obtain the basic formula. 2 In the usual month of 30 or 31 days, so that we can use
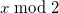 to get alternately 1 or 0, and then just add a constant to this number:
to get alternately 1 or 0, and then just add a constant to this number: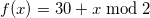
We get the table, the correct values are highlighted in bold:
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x) | 31 | thirty | 31 | thirty | 31 | thirty | 31 | thirty | 31 | thirty | 31 | thirty |
Not a bad start! There are already correct values for January and for the months from March to July inclusive. February is a special case, and we'll figure it out a little later. After July, for the remaining months, the order of receiving 0 and 1 should be reversed.
To do this, we can add to the dividend 1:
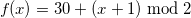
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x) | thirty | 31 | thirty | 31 | thirty | 31 | thirty | 31 | thirty | 31 | thirty | 31 |
Now the correct values are from August to December, but, as expected, the values for the other months are incorrect. Let's see how we can combine these formulas.
Mask overlay
For this, a piecewise-defined function is necessary, but - since it seemed boring to me - I thought about a different solution using one part of the function on one interval, the other on the other.
I believe that the easiest way is to find an expression equal to 1 in one application and 0 in the rest. The method in which multiplying the argument by the expression we exclude it from the formula outside its scope, I called the “mask overlay”, because this behavior is similar to a bit mask.
To use this method in the last part of our function, you need to find an expression equal to 1 for
 , and - since the argument values are always less than 16 - the integer division by 8 is perfect for this.
, and - since the argument values are always less than 16 - the integer division by 8 is perfect for this.| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ⌊ x ⁄ 8 ⌋ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | one | one | one | one | one |
Now using this mask using in delimited
 expression
expression  instead of 1, we can replace the order of getting 0 and 1 formula with the reverse:
instead of 1, we can replace the order of getting 0 and 1 formula with the reverse: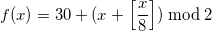
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x) | 31 | thirty | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
Eureka! Everything is correct, except February. Surprise surprise.
February
In any month 30 or 31 days, except February with its 28th (leap year is beyond the scope of this task). 3 At the moment, according to our formula, it has 30 days, so it would be nice to subtract an expression equal to 2 when
 .
.The best I managed to think of
 that puts a mask on all months after February:
that puts a mask on all months after February:| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 mod x | 0 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
Changing the base constant to 28 with the addition of 2 to the remaining months, we obtain the formula:

| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x) | 29 | 28 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
Unfortunately, January is now shorter by 2 days. But, fortunately, to get an expression that will only be used for the first month is very easy: it’s a rounded down reverse to
 number. Multiplying it by 2 yields the final formula:
number. Multiplying it by 2 yields the final formula:
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x) | 31 | 28 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
Afterword
Here it is - a formula for obtaining the number of days in any month of the year, using simple arithmetic. The next time you remember how many days in September, just follow
 using this single line javascript function:
using this single line javascript function:function f(x) { return 28 + (x + Math.floor(x/8)) % 2 + 2 % x + 2 * Math.floor(1/x); } Part II
Introduction
In the first part, a short and even slightly elegant formula was obtained, the main advantages of which are the simplicity of the mathematical apparatus, the absence of branching and conditional expressions, conciseness. The disadvantages - besides the fact that you will not apply it in your project - can be attributed to the absence of a check for a leap year and a non-leap year.
Therefore, I set myself the task to create a function f , such that the value of f (x, y) for each month x , represented by a number from 1 to 12 and the year y greater than 0, equals the number of days in month x in the year y .
For the impatient under the spoiler is a ready answer, the rest, please follow me.
Answer

The remainder of the division: mod and ⌊⌋
For visual clarity, we agree that in some formulas the division operator with the remainder is replaced by bottom brackets, where it seemed necessary to me:

Leap year
An additional calendar day is introduced in a leap year: February 29. As you know, a leap year is a multiple of 4 and not a multiple of 100, or a multiple of 400. We write the expression identical with this statement:

To bring this expression into algebraic, you must apply to the result of the expression
 injection form:
injection form:
That will allow you to get 1 when dividing without remainder and 0 when dividing with remainder, to use it in the formula for determining the number of days in a month.
As a function of g ', you can use 1 minus the remainder of the division
 for
for 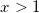 :
:| x | 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g '(x) | Infinity | one | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
It is easy to see that increasing the dividend and the divisor by 1, we get the correct formula
 at
at  :
:| x | 0 | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g '(x) | one | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Thus the expression
 write as:
write as:
And the expression
 write as:
write as:
Applying this approach, we obtain the following function g (y) , the value of which will be 1 if the year is a leap year, or 0 in the opposite case:

| y | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| g (y) | 0 | 0 | one | 0 | 0 | 0 | one | 0 | 0 | 0 | one |
| y | 2000 | 2100 | 2200 | 2300 | 2400 | 2500 | 2600 | 2700 | 2800 | 2900 | 3000 |
| g (y) | one | 0 | 0 | 0 | one | 0 | 0 | 0 | one | 0 | 0 |
Leap years are highlighted in bold.
I remind you that within the framework of the accepted agreement, the operator for obtaining the remainder of division can be depicted as mod and ⌊⌋.
Mask overlay
In the formula
 part
part  is an amendment, adding 2 days to January. If we remove the factor 2 and replace the numerator with 1 by 2, then this formula will add 2 days to January and 1 day to February, which gives us the key to adding a day in a leap year. For clarity, we use the intermediate value of g (y) in the formula and use 2000 (leap) and 2001 (not leap) years as y :
is an amendment, adding 2 days to January. If we remove the factor 2 and replace the numerator with 1 by 2, then this formula will add 2 days to January and 1 day to February, which gives us the key to adding a day in a leap year. For clarity, we use the intermediate value of g (y) in the formula and use 2000 (leap) and 2001 (not leap) years as y :
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x, 2000) | 31 | 29 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
| f (x, 2001) | thirty | 28 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | thirty |
Values for all months except January are not leap years are correct.
To correct this unfortunate misunderstanding, add to January 1 day already known to us by the formula
 :
:
| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x, 2000) | 32 | 29 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
| f (x, 2001) | 31 | 28 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | thirty |
Now you need to subtract 1 day from January in the case of a leap year, for which we will be helped by the knowledge that for any x
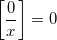 , but
, but  .
.Then the formula will look like:


Or:

| x | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f (x, 2000) | 31 | 29 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | 31 |
| f (x, 2001) | 31 | 28 | 31 | thirty | 31 | thirty | 31 | 31 | thirty | 31 | thirty | thirty |
Conclusion
As a result, a much more cumbersome, but more universal formula has been obtained, which can also be used to obtain the number of days in a month of a particular year:
function f(x, y) { return 28 + ((x + Math.floor(x / 8)) % 2) + 2 % x + Math.floor((1 + (1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1))) / x) + Math.floor(1/x) - Math.floor(((1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1)))/x); } An example in C # ideone.com/fANutz .
1 . I do not know how to use this mnemonic, so I spied on the tablet on the Internet.
2 "Basics," or "Rule With Many Exceptions," like most rules.
3 Initially, in the Roman calendar, February was the last month of the year, so there is a logic that it is shorter than all the others. There is also a logic to add or delete a day at the end of the year, so its length is variable.
Upd. one:
An alternative translation of the first part in the community VKontakte .
Upd. 2: Thanks to the keksmen commentary, the error in the leap year definition formula ( g (y) ) was corrected and the final formula was corrected.
Source: https://habr.com/ru/post/261773/
All Articles