Magic of tensor algebra: Part 2 - Vector and tensor operations. Ranks of tensors

Content

Introduction

Inexpressibly glad that readers liked the previous article . Immediately make a reservation - just talk about such a capacious concept of how the tensor does not work - the amount of information is large. I can promise that by the end of the cycle the mosaic will develop.

And last time we stopped at that, having considered the representation of a vector in an oblique basis, and determining that it is represented by two different (covariant and contravariant) sets of coordinates, we obtained general expressions for the scalar product, taking into account the change in the metric of space. Thus, we very carefully approached the notion of tensor

Tensor is a mathematical object that does not change with a change in the coordinate system, represented by a set of> its components and a rule for transforming components when changing the basis.

Scalar product is good. But what about the other operations? How do they relate to the geometry of space and can they be represented in a tensor form? Of course, representable, because vectors are ... tensors! And scalars are also tensors. Mathematical objects we are used to are only partial examples of a more general concept, which is a tensor.
')
Here we will also talk about it under a cat.

1. The geometric meaning of the metric tensor

For clarity, which does not greatly affect the generality of reasoning, we restrict ourselves to three-dimensional space. Let us prove the following statement: the determinant of the metric tensor is equal to the square of the volume of the parallelepiped stretched over the vectors of the basis.

$\ det | g_ {ij} | = \ mathcal {V} ^ 2 \ quad (1)$

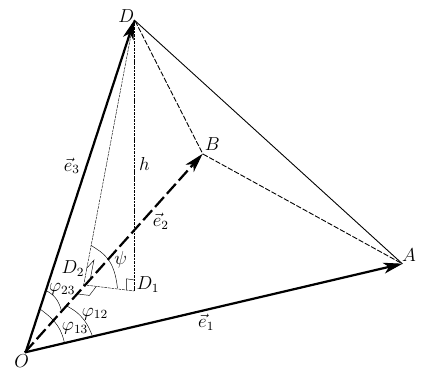
Fig. 1. Ratios in the triangular angle formed by the base

Consider an arbitrary basis.

$\ varphi_ {12} + \ varphi_ {13} + \ varphi_ {23} & lt; 2 \, \ pi$

Calculate the volume of the parallelepiped stretched on a basis as is customary in stereometry

$\ mathcal {V} = S \, h \ quad (2)$

where S is the base area of the parallelepiped; h - height, held to this base.

The area of the base is calculated trivially - as a module of a vector product.

$S = \ left | \ vec {e} _1 \ times \ vec {e} _2 \ right | = e_1 \, e_2 \ sin \ varphi_ {12} \ quad (3)$

With the determination of the height will have to tinker. If we knew the angle $\ psi$ then you would easily find the height

$h = DD_2 \ sin \ psi = e_3 \ sin \ varphi_ {23} \ sin \ psi \ quad (4)$

Angle $\ psi$ associated with linear and dihedral angles of a trihedral angle

$\ cos \ varphi_ {13} = \ cos \ varphi_ {12} \, \ cos \ varphi_ {23} + \ sin \ varphi_ {12} \, \ sin \ varphi_ {23} \ cos \ psi$

- the first cosine theorem for a trihedral angle. From it we express the cosine of the dihedral angle

$\ cos \ psi = \ frac {\ cos \ varphi_ {13} - \ cos \ varphi_ {12} \, \ cos \ varphi_ {23}} {\ sin \ varphi_ {12} \, \ sin \ varphi_ {23} } quad (5)$

The square of the sine of the angle we need is expressed in terms of the resulting cosine

$\ sin ^ 2 \ psi = 1 - \ cos ^ 2 \ psi \ quad (6)$

Perform successive substitutions from (6) to (2), not forgetting to square S and height h . The calculations are quite cumbersome and you can use SKA (Maple or Mathematica) to get them and get the square of the parallelepiped volume

$\ mathcal {V} ^ 2 = e_1 ^ 2 \, e_2 ^ 2 \, e_3 ^ 2 \ left (1 + 2 \ cos \ varphi_ {12} \ cos \ varphi_ {13} \ cos \ varphi_ {23} - \ cos ^ 2 \ varphi_ {12} - \ cos ^ 2 \ varphi_ {13} - \ cos ^ 2 \ varphi_ {23} \ right)$

Now we calculate the determinant of the metric tensor. It is called the determinant of the matrix, which is composed of the components of the tensor. The scalar products of the vectors of the basis we write into it explicitly

$\ det | g_ {ij} | = \ left | \ begin {matrix} e_1 ^ 2 & amp; & amp; e_1 \, e_2 \ cos \ varphi_ {12} & amp; & amp; e_1 \, e_3 \ cos \ varphi_ {13} \\ e_1 \, e_2 \ cos \ varphi_ {12} & amp; & amp; e_2 ^ 2 & amp; & amp; e_2 \, e_3 \ cos \ varphi_ {23} \\ e_1 \, e_3 \ cos \ varphi_ {13} & amp; & amp; e_2 \, e_3 \ cos \ varphi_ {23} & amp; & amp; e_3 ^ 2 \ end {matrix} \ right |$

Calculating it, we get the same result as for the square of the volume

$\ det | g_ {ij} | = e_1 ^ 2 \, e_2 ^ 2 \, e_3 ^ 2 \ left (1 + 2 \ cos \ varphi_ {12} \ cos \ varphi_ {13} \ cos \ varphi_ {23} - \ cos ^ 2 \ varphi_ {12 } - \ cos ^ 2 \ varphi_ {13} - \ cos ^ 2 \ varphi_ {23} \ right)$

Thus, statement (1) is true. Accordingly, the volume of the parallelepiped stretched on a basis can be obtained by extracting the root from the determinant of the metric tensor

$\ mathcal {V} = \ sqrt g \ quad (7)$

Where $g = \ det | g_ {ij} |$ for brevity, we denote the value of the determinant.

Root (7) is often found in the literature on GR and alternative theories of gravity of the RTG type. This value is of fundamental importance and will be useful to us a little later.

2. Tensor product of vectors. Dyad. The rank of the tensor. Convolution

Pay attention to the expression of the scalar product.
$c = g_ {ij} \, a ^ j \, b ^ i$
Magnitude

$C ^ {ji} = a ^ j \, b ^ i \ quad (8)$

called the tensor product of two vectors or a dyad . This product is called tensor because tensors are multiplied and a tensor is obtained at the output, in this case of the second rank, $C ^ {ji}$ . The rank of a tensor is the number of its indices. The vector, suddenly, is also a tensor, only of the first rank. Yes, this is understandable - after all, a vector, as a geometric entity, does not depend on the coordinate system in which it is considered. Only its components depend on the choice of a coordinate system.

The second rank tensor (8) is, of course, represented by its component matrix.

$\ mathbf {C} = \ begin {bmatrix} a ^ 1 \, b ^ 1 & amp; & amp; a ^ 1 \, b ^ 2 & amp; & amp; a ^ 1 \, b ^ 3 \\ a ^ 2 \, b ^ 1 & amp & amp; a ^ 2 \, b ^ 2 & amp; & amp; a ^ 2 \, b ^ 3 \\ a ^ 3 \, b ^ 1 & amp & amp; a ^ 3 \, b ^ 2 & amp; & amp; a ^ 3 \, b ^ 3 \ end {bmatrix} \ quad (9)$

Using (8) you can rewrite the scalar product in the form

$c = g_ {ij} C ^ {ji} \ quad (10)$

this is also a tensor product, called convolution because of the decrease in the rank of the resulting tensor. All indices in (10) are “mute”, they are double summed by the components of the metric tensor and dyad, and the output is the number c .

Attentive reader will say that the output should get a tensor. So the tensor is obtained - a scalar, this is also a tensor. Zero rank, since it has no indices and is not subject to conversion when changing the basis. The scalar product is invariant with respect to a change of the base, because neither the length of the vectors participating in it nor the angle between them from the change of the base changes. So the scalar is a zero-rank tensor.

But not any number is a scalar. A scalar is the length of a vector, the scalar product of vectors, the mass of the material body, the absolute temperature, and other quantities that are independent of the coordinate system. The vector component is no longer a scalar - it changes when the basis is changed.

We will talk about the rank of the tensors and the type of the components a bit later, but for now let's move on to the next burning question.

3. Vector product. Tensor Levi-Civita

Let us return to our vectors and perform their vector multiplication.

$\ vec {c} = \ vec {a} \ times \ vec {b} = \ left (a ^ 1 \, \ vec {e} _1 + a ^ 2 \, \ vec {e} _2 + a ^ 3 \ , \ vec {e} _3 \ right) \ times \ left (b ^ 1 \, \ vec {e} _1 + b ^ 2 \, \ vec {e} _2 + b ^ 3 \, \ vec {e} _3 \ right)$

In the absence of other options, carefully open the parentheses, bearing in mind the noncommutativity of the operation

$\ vec {c} = & amp; \ quad a ^ 1 \, b ^ 1 \ left (\ vec {e} _1 \ times \ vec {e} _1 \ right) + a ^ 2 \, b ^ 1 \ left (\ vec {e} _2 \ times \ vec {e} _1 \ right) + a ^ 3 \, b ^ 1 \ left (\ vec {e} _3 \ times \ vec {e} _1 \ right) +$

$a ^ 1 \, b ^ 2 \ left (\ vec {e} _1 \ times \ vec {e} _2 \ right) + a ^ 2 \, b ^ 2 \ left (\ vec {e} _2 \ times \ vec {e} _2 \ right) + a ^ 3 \, b ^ 2 \ left (\ vec {e} _3 \ times \ vec {e} _2 \ right) +$

$+ a ^ 1 \, b ^ 3 \ left (\ vec {e} _1 \ times \ vec {e} _3 \ right) + a ^ 2 \, b ^ 3 \ left (\ vec {e} _2 \ times \ vec {e} _3 \ right) + a ^ 3 \, b ^ 3 \ left (\ vec {e} _3 \ times \ vec {e} _3 \ right)$

Of course, we studied well at the university and we know that the vector product of the vector itself is zero. But we will not be in a great hurry with simplification, for besides this undoubtedly pleasant fact, we see one more thing - the components of the dyad (9). But apart from the simplification associated with the zero product of collinear vectors, we no longer observe anything. We work with an arbitrary basis in its pure form.

Apply a trick - multiply the vector $\ vec {c}$ scalar on the first basis vector $\ vec {e} _1$ considering now that the works $\ vec {e} _i \ times \ vec {e} _i = 0, \ quad i = \ overline {1,3}$

$\ vec {c} \ cdot \ vec {e} _1 = a ^ 2 \, b ^ 1 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e } _1 \ right) \ right] + a ^ 3 \, b ^ 1 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _1 \ right) \ right] + a ^ 1 \, b ^ 2 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _2 \ right) \ right] +$

$+ a ^ 3 \, b ^ 2 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _2 \ right) \ right] + a ^ 1 \ , b ^ 3 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _3 \ right) \ right] + a ^ 2 \, b ^ 3 \ , \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _3 \ right) \ right]$

Odds in square brackets are mixed products of vectors. If the vectors are coplanar (lie in the same plane), then such a product is zero. That is, if at least one vector repeats in a mixed product, it is equal to zero. So we are left with only two of the nine terms in which the vectors do not repeat with mixed multiplication.

$\ vec {c} \ cdot \ vec {e} _1 = a ^ 3 \, b ^ 2 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _3 \ times \ vec {e } _2 \ right) \ right] + a ^ 2 \, b ^ 3 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _3 \ right) \ right]$

So, now remember that $\ vec {c} \ cdot \ vec {e} _1 = c_1$ - covariant vector component $\ vec {c}$ . Finally, we rearrange the vectors in the vector product of the first addend, adding a minus as it should be, according to the rule of the vector product

$c_1 = a ^ 2 \, b ^ 3 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _3 right) \ right] - a ^ 3 \, b ^ 2 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _3 \ right) \ right] \ quad (11)$

Similarly select the other components.

$c_2 = \ vec {c} \ cdot \ vec {e} _2 = a ^ 3 \, b ^ 1 \, \ left [\ vec {e} _2 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _1 \ right) \ right] - a ^ 1 \, b ^ 3 \, \ left [\ vec {e} _2 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _1 \ right) \ right] \ quad (12)$

$c_3 = \ vec {c} \ cdot \ vec {e} _3 = a ^ 1 \, b ^ 2 \, \ left [\ vec {e} _3 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _2 \ right) \ right] - a ^ 2 \, b ^ 1 \, \ left [\ vec {e} _3 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _2 \ right) \ right] \ quad (13)$

Expressions (11) - (13) are very similar to the formula for calculating the projections of the vector product from the course of vector algebra, up to a factor with a mixed product. But we are not working on a Cartesian basis, it is natural to expect some difference. By the way, what is this multiplier? After all, the mixed product of vectors has a geometrical meaning ... This is ... the volume of the parallelepiped stretched by the vectors in it involved. And the volume of the parallelepiped stretched on the basis is the root of the determinant of the metric tensor! I.e

$\ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _3 \ right) \ right] = \ left [\ vec {e} _2 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _1 \ right) \ right] = \ left [\ vec {e} _3 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _2 \ right ) \ right] = \ mathcal {V} = \ sqrt g \ quad (14)$

So she floated to the surface, the metric of the space used. Thus, it is possible to construct a certain tensor, the convolution of the initial vectors with which gives a covariant vector, which is the result of a vector product. Moreover, this tensor is connected with the metric tensor. Such a third-rank tensor bears the name of the Italian mathematician Levi-Civita.

It is not difficult to see that the components of the Levi-Civita tensor are determined by the relation

$\ varepsilon_ {ijk} = \ vec {e} _i \ cdot \ left (\ vec {e} _j \ times \ vec {e} _k \ right) \ quad (15)$

There will be 27 of them, but most of them, namely 21 are zero. These are the components whose indices are repeated at least once. There are only six non-zero components; they correspond to non-repeating indices. Modulo they are equal $\ sqrt g$ , but three of them are positive, the other three are negative. In formulas (11) - (13) we rearranged the vectors and added minuses to make the coefficients in dyads positive and the formulas themselves similar to the vector algebra we are used to in the course. Now we will return everything to its place

$c_1 = a ^ 2 \, b ^ 3 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _3 \ right) \ right] + a ^ 3 \, b ^ 2 \, \ left [\ vec {e} _1 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _2 \ right) \ right] \ quad (16)$

$c_2 = a ^ 3 \, b ^ 1 \, \ left [\ vec {e} _2 \ cdot \ left (\ vec {e} _3 \ times \ vec {e} _1 \ right) \ right] + a ^ 1 \, b ^ 3 \, \ left [\ vec {e} _2 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _3 \ right) \ right] \ quad (17)$

$c_3 = a ^ 1 \, b ^ 2 \, \ left [\ vec {e} _3 \ cdot \ left (\ vec {e} _1 \ times \ vec {e} _2 \ right) \ right] + a ^ 2 \, b ^ 1 \, \ left [\ vec {e} _3 \ cdot \ left (\ vec {e} _2 \ times \ vec {e} _1 \ right) \ right] \ quad (18)$

The sign of mixed products depends on the order of the indices: in sets (1,2,3), (2,3,1), (3,1,2) they are positive, in sets (1,3,2), (2,1 , 3) and (3,2,1) - are negative. It is known that if the vectors are given in the right coordinate system, then their mixed product will be positive if they form the right three of vectors. In the first addends (16) - (18), the right triples of the basis vectors appear. Secondly, the same vectors participate in the mixed product, but taken as the left triple.

How to determine which top three give the basic vectors? It's very simple, because they are ordered, they are assigned numbers 1, 2, 3. If we follow the order of the vectors, we get a three corresponding to the used coordinate system, that is (1,2,3) - the right three.

And if we take the first vector 2? Then it should be followed by vector 3, in order. And which one is next? And the next vector 1, we start all over again, but without disrupting the order of the vectors, that is, (2,3,1) is the right triple, and (3,1,2) is also the right triple. In the language of combinatorics, the basis vectors in an ordered triple form an even permutation (that is, not violating the order of the elements). If the order of the trace vectors in the triples is the inverse of the adopted, then their permutation will be odd. Thus, the permutations (3,2,1), (2,1,3), (1,3,2) are odd, and the triples of vectors are left.

Using all of the above, we introduce the function

$P (i, j, k) = \ begin {cases} +1, \ quad \ quad (i, j, k) \, \ quad \ text {Even permutation} \\ -1, \ quad \ quad (i, j, k) \, \ quad \ text {Odd permutation} \ end {cases} \ quad (19)$

and, based on (14) and (19), we finally write out the Levi-Civita tensor

$\ varepsilon_ {ijk} = \ begin {cases} + \ sqrt g, \ quad P (i, j, k) = +1 \\ - \ sqrt g, \ quad P (i, j, k) = -1 \ \ \ quad 0, \ quad i = j \ vee j = k \ vee k = i \ end {cases} \ quad (20)$

for the right coordinate system

$\ label {eq: left-levy-chivit} \ varepsilon_ {ijk} = \ begin {cases} - \ sqrt g, \ quad P (i, j, k) = +1 \\ + \ sqrt g, \ quad P (i, j, k) = -1 \\ quad 0, quad i = j \ vee j = k \ vee k = i \ end {cases} \ quad (21)$

for the left coordinate system.

After that you can write the expression for the vector product in the tensor form

$c_i = \ varepsilon_ {ijk} \, a ^ i \, b ^ j \ quad (21)$

Thus, a vector product is a convolution of a dyad by the Levi-Civita tensor, which gives a covector at the output — that is, a vector defined by covariant components.

4. Mixed (vector-scalar) product of vectors

Armed with the knowledge gained, we now consider such an operation.

$v = \ vec {a} \ cdot (\ vec {b} \ times \ vec {c})$

Without operating with vectors, we will try to write it down immediately in a tensor form. First, the scalar product is commutative, therefore

$\ vec {a} \ cdot (\ vec {b} \ times \ vec {c}) = (\ vec {b} \ times \ vec {c}) \ cdot \ vec {a}$

And now we recall that the scalar product can be painted as a tensor
vector covector

$g_ {ij} \, a ^ i \, b ^ j = a_i b ^ j$

Vector product, based on (21), just gives a covector, which means

$\ varepsilon_ {ijk} \, b ^ j \, c ^ k = f_i \ quad \ Rightarrow \ quad v = f_i \, a ^ i = \ varepsilon_ {ijk} \, b ^ j \, c ^ k \, a ^ i$

That is, finally, a mixed product in tensor form

$v = \ varepsilon_ {ijk} \, a ^ i \, b ^ j \, c ^ k \ quad (22)$

where the Levi-Civita tensor is involved again.

Expression (22) could be obtained using vectors, coming back to the definition of the Levi-Civita tensor, but, as can be seen, it is more rational to use a tensor notation.

5. The rank of the tensor. Covariant and contravariant components

So, in the process of parsing vector operations, we came to the conclusion that tensors are mathematical objects, generalizing properties and operations on many mathematical objects known to us. Both scalars and vectors are tensors. They differ in rank and number of covariant and contravariant components. The rank is equal to the total number of indices of the tensor, and is denoted by a pair of integers in brackets ( p, q ), where p is the number of contravariant indices, q is the number of covariant indices. The tensor is said to be p- times contravariant and q- times covariant, of rank p + q .

The rank tensor (0,0) is a scalar, a quantity whose value can be expressed by a single number, with a value invariant with respect to a change in the coordinate system. The scalar has no indices, and it is not converted at all when the basis is changed. But, again, not every number is a scalar. For example, a component of a vector or a tensor is not a scalar, because it changes when the basis is changed.
Tensor rank (1.0) - vector. For a vector, a contravariant representation is natural. To calculate the scalar product of vectors, their convolution with the metric tensor is required.

The transformation of the vector components is performed by applying a linear operator to it, essentially multiplying the transformation matrix by the column containing the vector components, which in the tensor form looks like

$\ tilde {a} ^ i = \ alpha_j ^ i \, a ^ j$
The rank tensor (0,1) is a covector. If a nondegenerate metric tensor is defined in the space under consideration

$\ det | g_ {ij} | ~ \ ne ~ 0$

That vector and covector are two different representations of the same geometric object - a vector. In the orthogonal basis (the vectors of which are mutually perpendicular), the contravariant and covariant coordinates coincide. The transition from one representation to another is performed by convolution with the metric tensor.

$a_i = g_ {ij} \, a ^ j, \ quad a ^ i = g ^ {ij} \, a_j$

Where $g ^ {ij}$ a countervariant metric tensor whose components are a matrix,
inverse matrix of tensor components $g_ {ij}$ .

For scalar multiplication of a covector by a vector, it is not necessary to use the metric tensor, it is produced by direct convolution with a vector.

$c = a_i \, b ^ i$

The transformation of the components of the covector is also performed by applying a linear operator to it, but unlike the vector, the row containing the components of the covector by the coordinate transformation matrix is multiplied

$\ tilde {a} _i = \ alpha_i ^ j \, a_j$
A tensor of rank (0,2) is a bilinear form, an example of which is the doubly covariant metric tensor g _ij . The components of the metric tensor are transformed by applying a linear coordinate transformation operator to it twice, which corresponds to multiplying the transposed transformation matrix by the metric tensor matrix and then multiplying the result by the transformation matrix

$\ tilde {g} _ {ij} = \ alpha_i ^ k \, \ alpha_j ^ l \, g_ {kl}$
The rank tensor (2.0) is an example of a dyad (8). In general, all rank (k, 0) tensors are called polyvectors or polyads (triads, tetrads, etc.), and they are formed as linear combinations of tensor products of the corresponding number of vectors. Their components are converted to the appropriate rank by the number of linear applications.
operators that transform the original vectors.
The tensor of rank (1,1) is a linear operator. An example would be a rotation matrix or any other transformation of the coordinates of vectors and covectors. In general, the use of a linear operator is reduced to the matrix multiplication operation.

$b ^ i = \ alpha_j ^ i \, a ^ j \ quad (23)$

Where $b ^ i$ - the result of the conversion; $a ^ j$ - source vector; $\ alpha_j ^ i$ - the matrix components of the linear operator. Consider the process of converting a linear operator. Let S be the transition matrix from one basis to another. Then, when changing the basis both vectors are transformed - both the argument and the result

$a^{i} = s_j^i \, a^{'j}, \quad b^{i} = s_j^i \, b^{'j} \quad (24)$

(24) (23)

$s_q^p \, b^{'q} = \alpha_k^p (\, s_j^k \, a^{'j})$

, $S^{-1}$

$b^{'q} = (\tilde{s}_p^q \, \alpha_k^p \, s_j^k) \, a^{'j} \quad (25)$

Where $\tilde{s}_q^p$ — $S^{-1}$ . ,

$b^{'q} = \alpha_j^{'q} \, a^{'j} \quad (26)$

(25) (26),

$\alpha_j^{'q} = \tilde{s}_p^q \, \alpha_k^p \, s_j^k$

: .