Creating the Droste effect in Wolfram Language (Mathematica)

Translation of the post by John McLune " Droste Effect with Mathematica ". The code given in the article can be downloaded at the end of the post.
I express my deep gratitude to Kirill Guzenko for his help in translating.

---

The Droste effect ( wiki ) is a recursive inclusion of an image of itself in itself. The name comes from the Droste cocoa powder, which in 1904 was sold in a package that showed the nurse who held the box that the nurse was on, and so on. The simplest implementation is to scale and transform the image, then place it on its unmodified exact copy, then start the process again. Take a look at a demonstration that uses original illustrations of Droste packaging. However, much more interesting results can be achieved if we use the theory of functions of a complex variable (PCT). Asher M.K. was the first to popularize the idea of conformal mappings in relation to images, but with the help of computers we can easily implement this idea in photographs to get something like this:



Yes, the idea is not new. However, when I decided to implement a similar effect, the methods that I found on the network seemed to me unsatisfactory. Some suggested a lot of handmade copy-and-paste type over images, in others there were problems with inconsistencies in resolution at the joints of parts of images. And, as usual, I came to the conclusion that Mathematica should be used here, or in this case Mathematica grid .

In essence, the idea is simple. We create an image where the pixel at position { x, y } of the resulting image is obtained from the pixel at position f [{ x, y }] of our original image. The magic is in choosing the function f itself . But before we get to this, we need to prepare something.
')
Currently, Mathematica does not contain an operation for arbitrary transformation of images, so first I have to implement them ( Post was written by John in the 7th version of Wolfram Mathematica, in the 8th version a special function ImageTransformation appeared for this purpose, which significantly reduces the code in John’s article - ed. ). The important point is to constantly calculate the color between the pixels to prevent resolution matching problems and unnecessary pixelation in enlarged areas of the image. My method is to linearly interpolate all the colors of pixels in each RGB channel for an image. This is the most computationally complex approach, especially with 10 megapixel source images, but it gives me the quality I need.



To compensate for this approach, I configured everything for parallel computing. To begin with, I used the parallelization tools built into Mathematica . Thus, instead of simply using Table to generate a grid of pixels, I created a function that calls Table to generate a layer of the final image, which is invoked in parallel by ParallelTable to redistribute work between several processor cores. So 3-4 lines more, but this is only half of the work on parallelization.





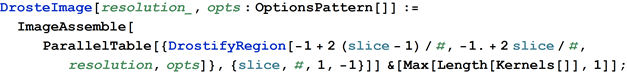
Then, I transfer the original image to each processor and set the interpolation function. This part is very demanding of calculations, so I want to do this only once and then be able to make any kind of images from the source without doing this work again. Parallelization is carried out here quite simply: the available cores are launched, the program definition is distributed to all cores, and then the ParallelEvaluate function is used to send an image by reference with a request to create an interpolation function.



There is an elegant way of transmitting an image as a string with the contents of a JPG file instead of transferring real uncompressed data. It turns out a much smaller object, which, accordingly, is transferred faster.

With such a setup, I can easily attract additional computer cores from my office to speed up computing using the Mathematica grid.

In the code you need to add something else. So I get rid of the need for the original image to be cropped in the right ratio and with the right centering.



Here's what my original image looks like after cropping:



Well, everything is boring behind, now is the time to have some fun.

The twist I use is based on the specific properties of the Power function Power on the complex plane. We can represent our pairs of coordinates { x, y } as parts of the complex number p = x + I y , use the map f [ p ]: = p ^c and go back to the Cartesian coordinates. It is rather difficult to figure out how to take the value of c , especially if you use the more general model a + ( b + c p ) ^d , where { a, b, c, d } are complex numbers. So I decided to turn to the Wolfram Demonstrations Project, found a demonstration with conformal mappings there and changed the code a bit to get the mapping I was interested in.

Having experimented, I found out the effects of the parameters, set up the calibration, got good initial values ​​and set the named options in the necessary places of that magic formula. In the end, I got this design for twisting.



I provide this kind of self-replication by jumping inside when I try to access a pixel outside the image, and then out while I get access to a pixel inside a certain area.

For reasons of aesthetics, I would like to close the connections between the images to make them more natural. In my example, I used a picture frame, but I found examples using doorways, windows, computer monitors, and the like.

Automating this process allows you to avoid manual copying and subsequent pasting, and also avoids problems with inconsistencies in the resolutions of different parts of the image.



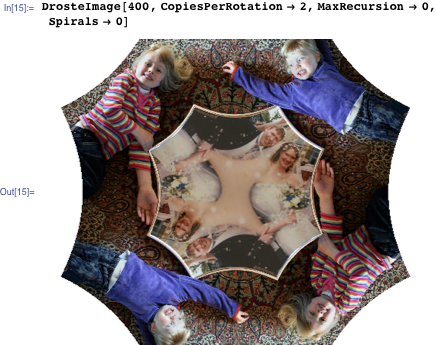
Everything, all the laborious work is over, now is the time to play around. Initialize the kernels with the original image, specifying the coordinates of the inner region (you can easily get them using the coordinate picker in the 2D Drawing palette):



Now generate an image with a height of 400 pixels in height:



There are many combinations of parameters, for example, like this one with a double helix:



One spiral in the opposite direction:



Without spirals, only replication:



This code creates octagons by creating two copies per spiral:



And this one without recursion and spirals is just two copies rolled together:



And here, the climax - a movie in DVD quality, showing the effect of Droste twisting the image into a recursive spiral.



Creating such a video requires a large amount of computation — calling three interpolation functions for each of 10 million pixels about 400 thousand times for each of 60 frames. This is the moment when my parallelization efforts really pay off. Of course, being at Wolfram Research, I have on hand several Mathematica grid licenses communicating via Wolfram Lightweight Grid Manager ( Starting from the 7th version of Wolfram Mathematica, the parallelization functionality is included in the Wolfram Language core and does not require additional programs when running it is able to use all the kernels available on your computer. However, if you need to connect to the cluster, this will require gridMathematica - ed. ). I open Parallel Configuration preferences, and they all magically appear. A few clicks, and now I have 16 more cores, in addition to two on my small laptop, and without any changes in the code, the film is generated 8 times faster (and 16 times faster than without parallelization). I don’t know exactly where this code works, but since the program and the source images are transmitted automatically, this is not very interesting for me. You can watch the on-screen demonstration of how all this is configured .



This code can be modified in different ways; for example, changing ReplicateRegion will allow you to use non-rectangular frames, in the form of circles, for example, or you can even change the colors and transparency of replications. Try experimenting yourself and see what can come of it.