How to write a simple solver tsumego

About a year ago, a friend showed me what a go is and how it is played. I remember well how in one of the first games I proudly built a chain of stones that connected the bottom side of the board with the top one, as well as the chain connecting the left side with the right one, to which a friend told me that it was nice, but I lost. It took me a long time to understand why. Since then I have progressed to about the first dan of KGS, and a friend stopped playing with me.

In order to play well go it is necessary to see several moves ahead, and this skill well develops a solution of which he has a lot of goproblems. Naturally, once the thought came to me that it would be nice to write the solution to these things and, ideally, embed it in goproblems, especially since adum approves of this idea. Since I myself solve tsumogo with a very unhurried search of more or less meaningful moves with a speed of somewhere 1 move in a couple of seconds, while regularly forgetting what the search began with (and this is enough to confidently solve problems 3 is given), I figured with what incredible speed and accuracy will work the simplest search in depth, I mean dfs, and I estimated the complexity of the task as “for a couple of days”. Immediately, I tried to quickly write this reshalker "on the forehead" through the simplest dfs and came across a minor nuisance: in the process of searching, the same positions were encountered many times and recounting them again was somehow completely non-optimal, even for a quick solver. Without thinking, I started a cache to store already resolved positions and immediately came across another nuisance: the solution found once may be wrong if another position comes in this position with a sequence of moves. I hung up here, not knowing what to do, but I decided that this trouble was easily solved - I just had to think a little. I thought for quite a long time and decided that it makes sense to look at what is already ready on this topic - articles, algorithms, etc. First of all, I came across a kind of “lambda depth first proof number search” and seeing that the size of the article was only a few pages, I began to read with delight. The article contained references to other similar articles by Martin Muller and Akiro Kishimoto, in those articles there are more links, there appeared a link to the 200-page dissertation of Kishimoto, and then I realized the scale of the problem: the solution of even very simple ones was so algorithmically complex that in most cases, the question is not even about how to sort through all the options, but how to find the total on the board (what even a novice player does in a second), how to understand what needs to be captured or defended (also trivial for a person) and what moves have The value (also in most cases obvious), and if it came to actually sorting through the options, then we can say that it’s decided (although the efficient brute force algorithm is extremely intricate). In general, I realized that my IQ is clearly not enough to solve this problem on the move and I decided that it would be nice if I could at least write a solver for the simplest case when all meaningful moves and goals are set in advance - even this will be very useful on goproblems.

As far as I know, there are quite a few programs that solve the problem:

- Thomas Wolf GoTools: up to 15 possible moves, closed code, rectilinear dfs with very advanced static analysis.
- Tsumego Explorer Martin Müller (which, by the way, is 7 dan): up to 30 possible moves, open source Java (although it’s not clear where to get), advanced l-df-pn-r search with very advanced static analysis described in the articles by Muller and thesis Kishimoto.
- Martin Müller's Fuego: a full 2+ bot is given (I can’t appreciate its power because it’s obviously stronger than me) with open source in C ++ (available on SourceForge).
')
Neither Muller nor adum heard about any js solvers (and the solver should be on js so that it can be embedded in goproblems), and if so, then it makes sense to try to write it — especially since Muller and Kishimoto wrote many articles and even programs on this topic.

Left typical tsumego. In the general case, the task is to find the best move (and if it is needed at all) for both black and white. Obviously, if whites go first, they capture the corner. If black goes first, they can keep the corner, but one of the decisions leads to ko and if black loses ko, they lose the angle, and the other solution keeps the angle without any ko, which is generally preferable.

For simplicity, we will assume that there is a certain way to look at the board and find out all meaningful moves that need to be searched for a solution (in fact, this means that all such moves will be set manually). We define the function R which says who wins on the board b:

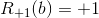• if black starts and wins.
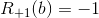• if black starts and loses.

By definition, R, black is obliged to make the first move, even if he breaks the balance in the seki - this allows you to eliminate the situation in which white and black constantly fold. Similarly for whites. If both black and white are losing, these are seki. Then this function can be recursively defined as:



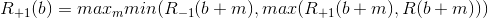
It looks a bit confusing, but its essence is simple:

1. By definition R, blacks are forced to make some kind of move, so they choose the best among all possible moves. Hence the maximum in all moves m.
2. Then the move goes to white and they can decide to make a move or not to do - hence the minimum. If White makes a move, the result will be 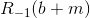where b + m is the b board to which was added a black stone m.
3. If White misses a move (and this does not contradict the definition of R), then Black has a choice: to make a move or also to fold, which will complete the game - hence the second maximum. If black makes a move, it turns out 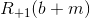if they pass, then R (b + m) determines who won (in practice, this is just a check to see if there is a stone on the board that should have been captured).

Symmetric formula is obtained for whites. If you count it “in the forehead,” you will get a straight dfs with an enumeration of all the options, which even for the simplest of 5 points works very slowly. You can write it like this:

function solve(board: Board, color: Color): Result { var result = -color; // that's a loss for (const move of board.getMovesFor(color)) { const nextBoard = board.fork().play(move); result = bestFor(color, // it's +color's turn, so he chooses result, bestFor(-color, // now it's -color's turn solve(nextBoard, -color), // -color makes a move bestFor(color, // -color can pass, but then it's +color's turn again solve(nextBoard, color), // +color makes two moves in a row estimate(nextBoard)))); // neither player makes a move } return result; } 

Please note that this algorithm will waste a lot of time on proving that the simplest seki is seki. If the white and black groups have only common freedoms and there are many of these freedoms, then this algorithm will first try to play on the first freedom, find out what to win does not work, then play on the second freedom and find out again what cannot be won, etc. You can even make up a simple recursive formula for the number of moves that this algorithm makes to sort through all the options. Growth is more than exponential. This problem can probably be solved only by static analysis.

Now we need to make sure that the same board is not solved twice. For example, having found once a solution for a 5-point nakad, you can reuse it if another position comes down to that nakad. Such a solution cache is usually called a transposition table (tt). The key in this table is the hash of the board + the color of the one who goes first. At first, I naively implemented it something like this:

 const tt: { [key: string]: Result } = {}; function solve(board: Board, color: Color): Result { const key = color + board.hash(); var result = -color; // that's a loss if (key in tt) return tt[key]; for (const move of board.getMovesFor(color)) { const nextBoard = board.fork().play(move); result = bestFor(color, // it's +color's turn, so he chooses result, bestFor(-color, // now it's -color's turn solve(nextBoard, -color), // -color makes a move bestFor(color, // -color can pass, but then it's +color's turn again solve(nextBoard, color), // +color makes two moves in a row estimate(nextBoard)))); // neither player makes a move } return tt[key] = result; } 

The problem with this code is that there are positions whose solution cannot be determined simply by looking at the location of the stones. For example, on the left, White’s move, but it is impossible to understand who wins, because it is unclear whether White can capture the black stone (ie, a typical ko or a two-stroke cycle). This minor amendment to the rules - you cannot repeat the position - is taken for granted during the game and does not cause any difficulties, and the super-ko rule (i.e., prohibiting cycles of several moves in length) was invented to resolve a situation that might not meet in your life even if you play ten games every day. Strangely enough, even the hypothetical possibility of the existence of cycles with a length of several moves (moves that way in 5-7) is certainly realized during an algorithmic search and if this is not taken into account, then either the result will be wrong or the algorithm will loop. So this seemingly virtual problem won Kisimoto’s thesis “The Correct and Efficient Search Algorithms in The Presence of Repetitions” by as much as 200 pages (I’m trying to master it myself).

The solution to this problem is mentioned many times in the articles by Muller and Kishimoto and it sounds like this: if there were no repetitions in the search for a solution, then it does not depend on the way in which you came to this position. If you think about it, the statement is not at all obvious. When I got tired of inventing evidence, I wrote to Muller and he said that yes, this is a very strong and universal statement and his proof seemed to be somewhere in the dissertation. I couldn’t find this evidence there, but I thought of my own, which works if we assume that all already-decided and independent solutions are never deleted (due to lack of memory).

For illustration, I shamelessly copied a picture from someone :) The graph of possible moves usually looks like this tree in the picture. The top in this graph is the location of the stones on the board, and the color indicates who makes the move. For simplicity (and without breaking the generality), we assume that position 13 was solved earlier and it turned out that Black starts and wins, while no cycles were found in the search process. The solution is a tree (because there is no), in which from each black vertex it leads one move (more is not necessary because the essence of the decision is to show the correct move in any position), and from each white vertex all possible moves lead (solution must prove that for every move of whites there is a move of black which leads to the victory of black). Now suppose that the statement is not true and the solution found for position 13 depends on the way in which it gets into it, i.e. there is some way that somehow makes the decision wrong. If such a path did not intersect with the decision tree, then it would not be able to influence it - then this hypothetical path contains at least one vertex of the tree. Take this top of some kind and try to go along this path to the top of 13 without forgetting that

1. the solution for 13 is already stored in the cache and what
2. all intermediate solutions that were also found without detecting the cycles remained in the cache.

Suppose that we start from vertex 17 and try to get to 13. The essence of the proof is that since there are no cycles in the decision tree, then for connecting 17 to 13 you need to go beyond the tree, which is impossible. Vertex 17 is white (well, yes, it is red, but we will assume that it is white) and therefore all the moves from it are in the tree: we make any move from 17 and still remain in the decision tree. Suppose we hit the 25 - black peak. Since the vertex is black, the solution (the right move) for it is written in the cache (from which nothing is ever removed), and since we are following this hypothetical path after the solution for 25 was found, we have to take the ready solution from the cache and get to the white top which is still in the tree. So we go on this hypothetical way until we find ourselves at an impasse where there are no moves.

As you can see, in order to solve the problem with cycles, you need quite a bit:

1. Search for a solution for the path, not for the position: solve (path: Board [], color: Color).
2. If in the process of searching we stumble upon a repetition, we consider it as a defeat, but at the same time we point to the peak in the path that repeats (just remember the index in the path). The meaning of the pair (result, index) is that the decision is not unconditional, but depends on repetition with a certain position.
3. If among all possible moves, all lead to defeat, we find the minimum among all indices indicating repetition and return this minimum.
4. If there are winning moves, then it is preferable to choose one with a repetition index as high as possible. At best, the gain will be unconditional, i.e. do not depend on the way.

This (and simple heuristics that maximizes the freedom of its stones and minimizes the freedom of others) is enough to solve the simplest carpenter square.

To solve something more interesting, like the first one, you need to be able to take into account ko. One possible approach is to take the “dynamically” into account, i.e. if a repetition occurs in the search process, branch the search into two cases (when there is a threat to and when it is not), but for this you have to thoroughly shovel the whole code. Another approach is “static” accounting for:

1. The new parameter is the number of external threats. Let's say if this parameter equals +3, then Black has three ko more threats, and if -2, then White has two ko more threats.
2. If there is a repetition in the decision process and there is a threat to this repetition, it is wasted, the path is reset (in fact, the goal of the threat is to clear the path and start the search as if from scratch).
3. Decisions in the cache are not written as a single number (+1 or -1), but an infinite array of numbers in both sides, where for each number of threats there is a result: for -2 kos, whites win, if White only has 1 k threat, then it turns out the seki, and if ko there are no threats, then black wins. Obviously, if black wins with N co-threats, then with N + 1 they will also win. Similarly for whites. This shows that the solution can be written in the form of two numbers: the number of co-threats that is black enough to win (maxb), and the number of co-threats that is white enough to win (minw). Then if we are looking for a solution for position b with k k threats and minw and maxb are known for b from previous solution attempts, then we can immediately return the answer for k <minw (white win) and for k> maxb (black win), and for minw <k <maxb need to look for a solution.

 interface Results { minw: number; // white wins if nkt <= minw maxb: number; // black wins if nkt >= maxb } const tt: { [key: string]: Results } = {}; function solve(path: Board[], color: Color, nkt: number): Result { function solveFor(color: Color, nkt: number): Result { const board = path[path.length - 1]; const key = color + board; const cached = tt[key] || { minw: -Infinity, maxb: +Infinity }; if (color > 0 && nkt >= cached.maxb) return +1; // black has enough ko treats to win if (color < 0 && nkt <= cached.minw) return -1; // white has enough ko treats to win var result = -color; // that's a loss var depth = Infinity; // where repetition occured /* ... */ if (color > 0 && nkt < cached.maxb) cached.maxb = nkt; if (color < 0 && nkt > cached.minw) cached.minw = nkt; tt[key] = cached; return [result, depth]; } return solveFor(color, nkt); } 

Now, to solve the problem taking into account external threats, we must first solve it under the assumption that there are no threats (nkt = 0) and continue to increase or decrease this parameter as long as this can change the result. This, theoretically, can be determined by a solution graph: if the solution found depends on the lost ko, then it makes sense to add one external threat and then solve it again. Practically, I did not do this, and the number of necessary threats is extremely rarely more than 1, i.e. there are problems in which you need to win two co to solve, but this is exotic, so if you solve tomgogo for | nk2 | <2, then you can say that the problem has been solved. It should be noted that 99% of the time it takes to find the first solution (usually for nkt = 0) which fills the cache (tt) after which the solutions for the other nkt are found almost instantly (even on JS).

That's all. Such a simple solver on JS without any optimizations that creates temporary objects for every sneeze (which it loads with GC), and before each move it copies the entire board, is able to quickly, in a few seconds, solve a sum with 10 free cells (like what I showed at the beginning). On a bit larger, it just hangs and will load the GC most of the time. However, in optimizations of this kind, I still do not see the point, because there are a lot of ways to make the algorithm itself faster:

• Apply advanced depth search: dfpn, dfpnr, ldfpnr. Muller writes that ldfpnr can overpower a sum with 27 free cells, which is a lot.
• Write static analysis algorithms - I haven't even implemented the Benson algorithm yet. This will stop the search when it is already clear who won. This is probably the main reason for the fact that we can solve this problem so quickly: usually the search for a solution in the mind looks like a search of several short sequences completed by the assessment “well, well, here, obviously, White is captured.”
• Think of how to look for the summit on the board and where to make the moves. To do this, it is necessary to “only” carefully observe our own thinking and understand exactly how we find the sum. The key to such a search, of course, is the assessment of the survivability of the group (a handful of closely spaced stones) which is based on determining whether the group can make two eyes: the sum is always near a weak and relatively large group (so that it makes sense to capture or save).
• Make a certain library of tricks (tesuji): squeeze, wedge, snapback, ladder, net, etc. These tricks play a huge role in finding a solution in the mind: we don’t count every time all possible options to find a snapback - we just notice a characteristic combination of stones and check whether something can be “squeezed out of this trick.”

Who cares , you can see the code on github . There, frankly, everything needs to be rewritten as soon as I understand how to organize the solver code so that it is broken into modules without sacrificing speed, and so that later it can be connected to modules responsible for static analysis, for recognizing seki, for different tricks etc. Well, so that you can write unit tests - otherwise, after each change, I think “does this crap still work?”