How to calculate load average

Statement of a question

Recently, during an interview in one large company, I was asked a simple question of what a Load Average is. I don’t know how correctly I answered, but I personally realized that I don’t really know the exact answer.

Most people probably know that Load Average is the average system load over a period of time (1, 5, and 15 minutes). You can also find out some of the details of this article , about how to use it. In most cases, this knowledge is enough to evaluate the system load by the LA value, but I am a physicist by specialty, and when I see the “average over a period of time” I immediately get interested in the sampling rate on a given interval. And when I see the term “waiting for resources”, it becomes interesting which ones and for how long you have to wait, as well as how many trivial processes need to be launched to get high LA in a short period of time. And most importantly, why the answers to these questions does not give 5 minutes of working with Google? If these details are just as interesting for you, welcome to Cat.

Something is wrong here...

For a start, let's define what we know. In a general way, Load Average is the average number of processes waiting for CPU resources for one of three time intervals. We also know that this value in the normal state is in the range from 0 to 1, and the unit corresponds to a 100% load on a single-core system without overload. In the future, I will consider the system as single-core, since it is simpler and more indicative.

What is wrong here?
')
First , we all know that the arithmetic average of several quantities is equal to the sum of these quantities divided by their number. From the information that we have absolutely incomprehensible this very amount. If we count the waiting processes for the whole minute, then the average value will be equal to the number of processes per minute divided by one. If we count every second, then the number of processes in each counting will decrease with the range, and divide by 60. Thus, the higher the sampling rate during data collection, the smaller the average value we get.

Second, what does the “resource-pending process” mean? If we launch a large number of fast processes at once, they will all stand in a queue, and logically, for a short period of time, LA should grow to completely unacceptable values, and during long-term monitoring, constant jumps should be observed, which, in a normal situation, does not.

Third , a single-core system with a 100% load should give the Load Average equal to 1. But here there is no dependence on the parameters of this core, although the number of processes may differ several times. This question can be removed either by the correct definition of the “process waiting for resources” or by the presence of some kind of normalization to the kernel parameters.

Literature

Finding answers to the questions posed was not so difficult. The truth is only in English, and not everything became immediately clear. Specifically, two articles were found:
"Examining Load Average"
"UNIX Load Average"
User Rondo also suggested the second part of the article with a more detailed review of the mathematical apparatus: “UNIX Load Average. Part 2
As well as a small test for those who already understand everything, mentioned in the second article.

I would advise those interested to read both articles, although very similar things are described in them. The first one describes in general terms many different interesting details of the system, while the second one describes LA calculations in more detail, gives examples of workload and comments from specialists.

Little nuclear magic

From these materials, you can learn that each process being called is given a limited period of time for using the CPU, in the standard intel architecture this period is 10ms. This is a whole hundredth of a second and in most cases the process does not need that much time. However, if a process has used all the time allotted to it, then a hardware interrupt is called and the system regains control of the processor. In addition, every 10ms increasing the tick counter (jiffies counter). These ticks are counted from the moment the system is started and every 500 ticks (once every 5 seconds) a Load Average is calculated.

The code of the calculation itself is located in the kernel in the file timer.c (the code is for version 2.4, in version 2.6 everything is somewhat dispersed, but the logic has not changed, then, I hope, there are no significant changes either, but, frankly, I did not check the latest releases) :

646 unsigned long avenrun[3]; 647 648 static inline void calc_load(unsigned long ticks) 649 { 650 unsigned long active_tasks; /* fixed-point */ 651 static int count = LOAD_FREQ; 652 653 count -= ticks; 654 if (count < 0) { 655 count += LOAD_FREQ; 656 active_tasks = count_active_tasks(); 657 CALC_LOAD(avenrun[0], EXP_1, active_tasks); 658 CALC_LOAD(avenrun[1], EXP_5, active_tasks); 659 CALC_LOAD(avenrun[2], EXP_15, active_tasks); 660 } 661 } 

As you can see, the same three values ​​of LA are calculated in turn, but it is not specified what exactly is considered, and how exactly is considered. This is also not a problem, the code for the count_active_tasks () function is in the same file, just above:

 625 static unsigned long count_active_tasks(void) 626 { 627 struct task_struct *p; 628 unsigned long nr = 0; 629 630 read_lock(&tasklist_lock); 631 for_each_task(p) { 632 if ((p->state == TASK_RUNNING || 633 (p->state & TASK_UNINTERRUPTIBLE))) 634 nr += FIXED_1; 635 } 636 read_unlock(&tasklist_lock); 637 return nr; 638 } 

And CALC_LOAD is in sched.h along with several interesting constants:

  61 #define FSHIFT 11 /* nr of bits of precision */ 62 #define FIXED_1 (1<<FSHIFT) /* 1.0 as fixed-point */ 63 #define LOAD_FREQ (5*HZ) /* 5 sec intervals */ 64 #define EXP_1 1884 /* 1/exp(5sec/1min) as fixed-point */ 65 #define EXP_5 2014 /* 1/exp(5sec/5min) */ 66 #define EXP_15 2037 /* 1/exp(5sec/15min) */ 67 68 #define CALC_LOAD(load,exp,n) \ 69 load *= exp; \ 70 load += n*(FIXED_1-exp); \ 71 load >>= FSHIFT; 

From all of the above, we can say that every 5 seconds the kernel looks at how many processes are in the RUNNING and UNINTERRUPTIBLE state (by the way, on other UNIX systems this is not the case) and for each such process it increases the counter on FIXED_1, which equals 1 << FSHIFT, or 1 << 11, which is equivalent to 2 ^ 11. This is done to simulate a floating-point calculation using standard int variables of a length of 32 bits. After offsetting the result by 11 bits to the right, we discard the extra orders. From the same sched.h:

  49 /* 50 * These are the constant used to fake the fixed-point load-average 51 * counting. Some notes: 52 * - 11 bit fractions expand to 22 bits by the multiplies: this gives 53 * a load-average precision of 10 bits integer + 11 bits fractional 54 * - if you want to count load-averages more often, you need more 55 * precision, or rounding will get you. With 2-second counting freq, 56 * the EXP_n values would be 1981, 2034 and 2043 if still using only 57 * 11 bit fractions. 58 */ 

A bit of nuclear decay

No, the core of the system does not break up here, just the CALC_LOAD formula, according to which Load Average is considered, is based on the law of radioactive decay , or simply exponential decay. This law is nothing but a solution of a differential equation. 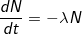that is, each new value is calculated from the previous one and the rate of decrease in the number of elements directly depends on the number of elements.
The solution of this differential equation is the exponential law:



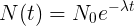
In fact, Load Average is not an average value in the usual sense of the arithmetic mean. This is a discrete function, periodically calculated from the moment the system starts. The value of the function is the number of processes working in the system under conditions of exponential decay.
We observe such a construction by rewriting the calculation part of CALC_LOAD in mathematical language:



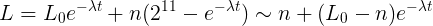
2 ^ 11 for us in this case is equivalent to one, we fixed it initially and added everywhere, the number of new processes is also calculated in these values. BUT 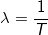where T is the measurement interval (1, 5 or 15 minutes).

It is worth noting that with a fixed time interval and a fixed time between measurements, the values ​​of the exponent can well be calculated in advance and used as a constant, which is done in the code. The last operation - shift to the right by 11 bits gives us the desired Load Average value with a drop of the lower orders.

findings

Now, understanding how LA is calculated, you can try to answer the questions posed at the beginning of the article:
1) The average value is not the arithmetic average, but is the average value of the function, which is calculated every 5 seconds from the moment the system starts.
2) "Waiting for CPU resources" are all processes in the RUNNING and UNINTERRUPTIBLE state. But we do not observe significant jumps of Load Average during long-term monitoring, since the decaying exponent plays the role of a smoothing function (although one can notice them when considering a period of 1 minute).
3) And here is one of the most interesting findings. The fact is that the above Load Average function for any value of n increases monotonically to this value, but if n <L, it decays exponentially to it. Thus, LA = 1 says that at any given time the CPU is occupied by a single process and there is no queue at all, which in general can be considered 100% load, no more, no less. At the same time, LA <1 says that the CPU is idle, and if you have a lot of processes that are knocking on non-working nfs, then you can see


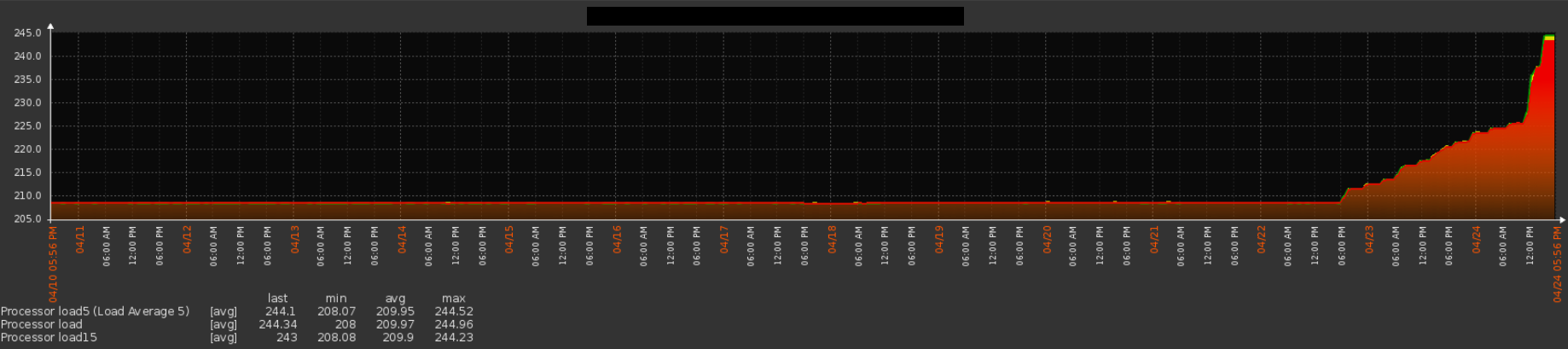
However, in addition to answering the questions that were available initially, the code analysis also puts new ones. For example, does the decaying exponent apply to reducing the number of pending processes? If we consider radioactive decay, then its speed is limited only by the number of cores, in our case, with a large number of processes, everything will all rest on the throughput of the CPU. Also, if we compare the resulting formula with the exponential law, it becomes clear that 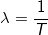where T is the duration of the data set interval (1, 5 or 15 minutes). Thus, the kernel developers believe that the decrease rate of the Load Average is inversely proportional to the duration of the measurements, which is somewhat unclear, at least for me. Well, it is not difficult to simulate situations where the huge values ​​of LA will not really display the system load, or vice versa.

In the end, it seems that for calculating the Load Average, a smoothing function was chosen, reducing its value as quickly as possible, which is generally logical for obtaining a finite number, but does not reflect the actual process. And if someone explains to me why an exhibitor and why exactly in this form, I will be very grateful.